Слайд 213. Законы Ньютоны для системы материальных точек.
Закон сохранения импульса.

Слайд 313. Законы Ньютоны для системы материальных точек.
Закон сохранения импульса.

Слайд 413. Законы Ньютоны для системы материальных точек.
Закон сохранения импульса.
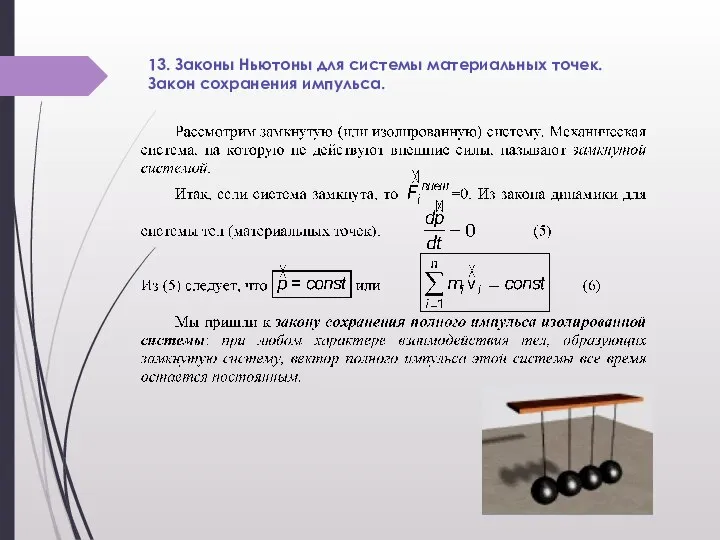
Слайд 513. Законы Ньютоны для системы материальных точек.
Закон сохранения импульса.

Слайд 614. Центр масс и его движение.
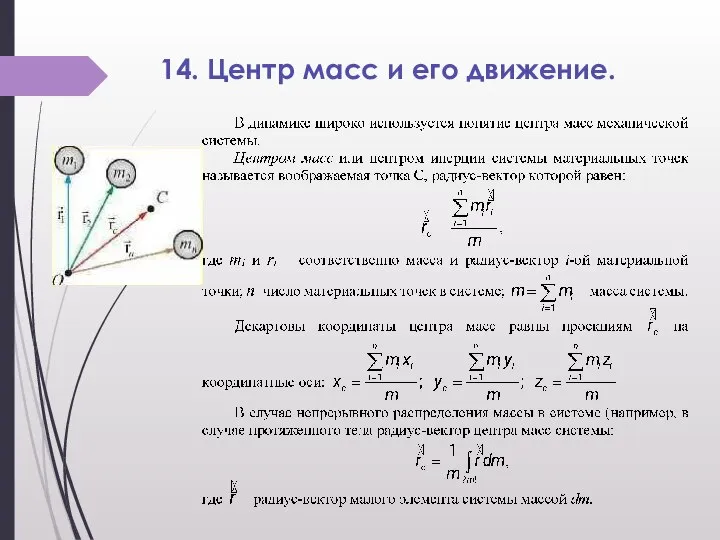
Слайд 714. Центр масс и его движение.

Слайд 815. Движение тел переменной массы.
В механике Ньютона считается, что масса тела не

зависит от скорости. Однако это не означает, что при движении тела его масса всегда остается постоянной. Она может изменяться вследствие изменения состава движущегося тела (вращающаяся катушка с кабелем, поливная маши-на, полет ракеты с работающими двигателями, когда выбрасываются продукты сгорания топлива).
Основное уравнение динамики материальной точки переменной массы впервые было получено И.В.Мещерским (1897 г.)
Слайд 915. Движение тел переменной массы.

Слайд 1015. Движение тел переменной массы.

Слайд 1116. Энергия системы материальных точек. Закон сохранения
механической энергии в консервативной системе.

Слайд 1216. Энергия системы материальных точек. Закон сохранения
механической энергии в консервативной системе.

Слайд 1316. Энергия системы материальных точек. Закон сохранения
механической энергии в консервативной системе.

Слайд 1417. Соударение двух тел.
Примером применения законов сохранения импульса и энергии при
решении реальной физической задачи является удар абсолютно упругих и неупругих тел.
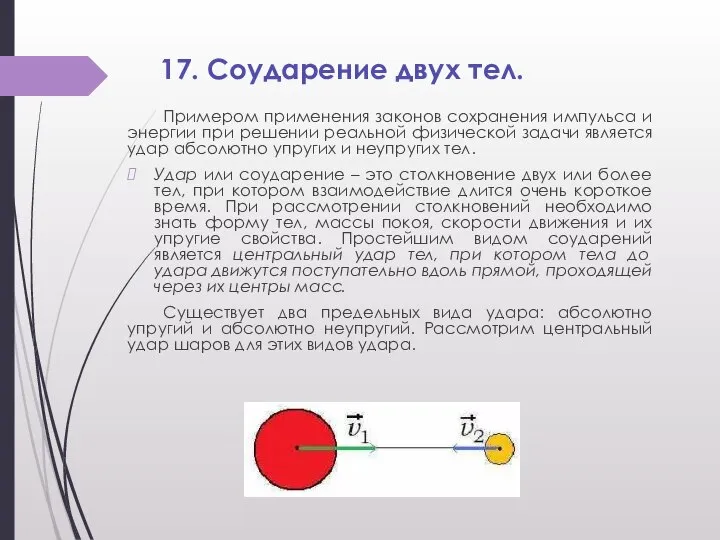
Удар или соударение – это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. При рассмотрении столкновений необходимо знать форму тел, массы покоя, скорости движения и их упругие свойства. Простейшим видом соударений является центральный удар тел, при котором тела до удара движутся поступательно вдоль прямой, проходящей через их центры масс.
Существует два предельных вида удара: абсолютно упругий и абсолютно неупругий. Рассмотрим центральный удар шаров для этих видов удара.
















 Механическая работа. Мощность
Механическая работа. Мощность Состав и строение атома
Состав и строение атома Ядерные реакции под действием нейтронов. (Тема 2.6)
Ядерные реакции под действием нейтронов. (Тема 2.6) Тема урока: Магнитное поле катушки с током. Электромагнит. Цель урока: исследовать зависимость силы магнитного поля катушки с токо
Тема урока: Магнитное поле катушки с током. Электромагнит. Цель урока: исследовать зависимость силы магнитного поля катушки с токо Назначение основных размеров опор и определение нагрузок, действующих на опоры
Назначение основных размеров опор и определение нагрузок, действующих на опоры Фотоэффект
Фотоэффект Мир вокруг нас
Мир вокруг нас Квантовая биофизика
Квантовая биофизика Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью Презентация на тему Электробезопасность
Презентация на тему Электробезопасность  Измерение cилы трения
Измерение cилы трения Задача №16 Магнитная пушка
Задача №16 Магнитная пушка Сиракузы. III век до нашей эры
Сиракузы. III век до нашей эры Основные понятия теории механизмов и машин
Основные понятия теории механизмов и машин Диоды Ганна
Диоды Ганна Неравномерное движение. Мгновенная скорость
Неравномерное движение. Мгновенная скорость Последовательное соединение
Последовательное соединение Звук и его характеристики
Звук и его характеристики Разнообразие веществ в окружающем мире
Разнообразие веществ в окружающем мире Презентация на тему Деление ядер урана Атомная энергетика
Презентация на тему Деление ядер урана Атомная энергетика  Аналогово-цифровой контроллер
Аналогово-цифровой контроллер Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Основные законы электрической цепи постоянного тока
Основные законы электрической цепи постоянного тока Основы квантовой физики
Основы квантовой физики Автосцепное устройство
Автосцепное устройство Воздухоплавание
Воздухоплавание Презентация на тему Молекулярная физика. Ученые и их открытия
Презентация на тему Молекулярная физика. Ученые и их открытия  Диагностика дизельных двигателей
Диагностика дизельных двигателей