Курс лекций по молекулярной физике и термодинамике

Курс лекций по молекулярной физике и термодинамике
Физика!
Т П У
Лектор – Поздеева Э.В.

Тема 2. РАСПРЕДЕЛЕНИЕ ГАЗОВЫХ МОЛЕКУЛ ПО СКОРОСТЯМ И ЭНЕРГИЯМ
2.1. Скорости газовых молекул. Опыт Штерна
2.2. Вероятность события. Понятие о распределении молекул газа по скоростям
2.3. Функция распределения Максвелла
2.4. Барометрическая формула
2.5. Распределение Больцмана
2.6. Закон распределения Максвелла-Больцмана
2.7. Распределение Бозе-Эйнштейна, Ферми-Дирака

2.1. Скорости газовых молекул. Опыт Штерна
В средине XIX века была сформулирована молекулярно-кинетическая теория, но тогда не было никаких доказательств существования самих молекул. Вся теория базировалась на предположении о движении молекул, но как измерить скорость их движения, если они невидимы.

Теоретики первыми нашли выход. Из уравнения молекулярно-кинетической теории газов известно, что
.
Отсюда среднеквадратичная скорость равна:
(2.1.1)

Получена хорошая формула для расчета среднеквадратичной скорости, но масса молекулы неизвестна.
Запишем по другому значение υкв:
(2.1.2)
А мы знаем, что , тогда
(2.1.3)
где Р – давление; ρ − плотность. Это уже измеряемые величины.

Например, при плотности азота, равной 1,25 кг/м3, при t = 0° С и , скорости молекул азота .
Для водорода:
При этом интересно отметить, что скорость звука в газе близка к скорости молекул в этом газе. Это объясняется тем, что звуковые волны переносятся молекулами газа.

O. STERN
Проверка того факта, что атомы и молекулы идеальных газов в термически равновесном пучке имеют различные скорости, была осуществлена немецким ученым Отто Штерном (1888 − 1969) в 1920 г.

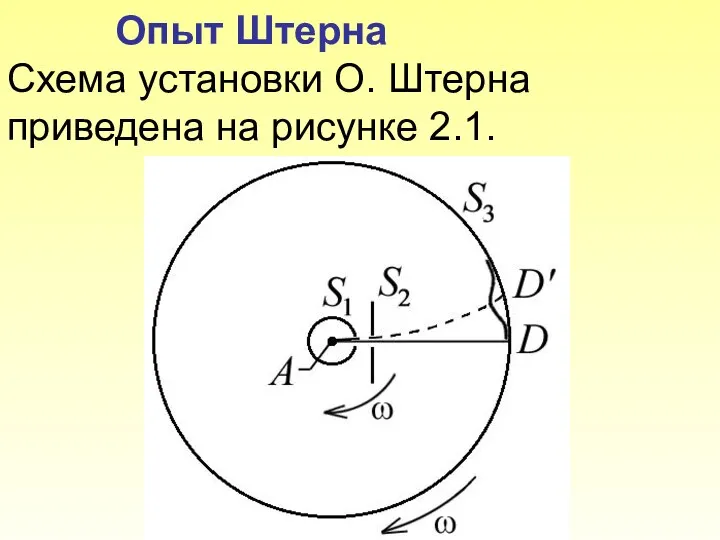
Опыт Штерна
Схема установки О. Штерна приведена на рисунке 2.1.
Рис. 2.1

Платиновая нить А, покрытая снаружи серебром, располагается вдоль оси коаксиальных цилиндров S1, S3. Внутри цилиндров поддержи-вается низкое давление порядка Па. При пропускании тока через платиновую нить она разогревается до температуры выше точки плавления серебра (961,9 °С). Серебро испаряется, и его атомы через узкие щели в цилиндре S1 и диафрагме S2 летят к охлаждаемой поверхности цилиндра S3, на которой они могут осаждаться. Если цилиндры S1, S3 и диафрагма не вращаются, то пучок осаждается в виде узкой полоски D на поверхности цилиндра S3.

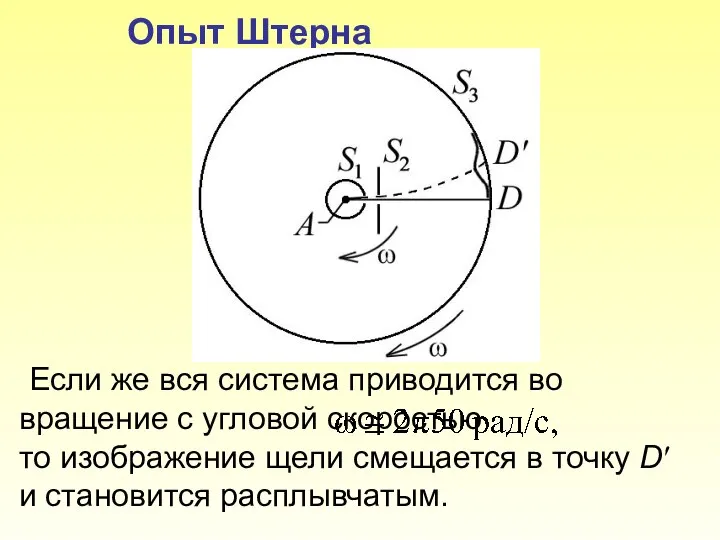
Опыт Штерна Если же вся система приводится во вращение с угловой скоростью то изображение щели смещается в точку D′ и становится расплывчатым.

Пусть l – расстояние между D и, измеренное вдоль поверхности цилиндра S3, где – линейная скорость точек поверхности цилиндра S3, радиусом R; − время прохождения атомами серебра расстояния . Таким образом, имеем откуда – можно определить величину скорости теплового движения атомов серебра:

Температура нити в опытах Штерна равнялась 1200°С, что соответствует среднеквадратичной скорости молекул серебра
В эксперименте получился разброс значений скорости от 560 до 640 м/с. Кроме того, изображение щели D′ всегда оказывалось размытым, что указывало на то, что атомы Ag движутся с различными скоростями.

Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно сталкиваясь друг с другом, как-то «распределяются» по скоростям, причём вполне определённым образом.
Таким образом, в этом опыте были не только измерены скорости газовых молекул, но и показано, что они имеют большой разброс по скоростям. Причина – в хаотичности теплового движения молекул.

2.2. Вероятность события.
Понятие о распределении молекул газа по скоростям
С точки зрения атомно-молекулярного строения вещества величины, встречающиеся в макроскопической физике, имеют смысл средних значений, которые принимают некоторые функции от микроскопических переменных системы. Величины такого рода называются статистическими. Примерами таких величин являются давление, температура, плотность и др.

Большое число сталкивающихся атомов и молекул обуславливает важные закономерности в поведении статистических переменных, не свойственные отдельным атомам и молекулам.
Такие закономерности называются вероятностными или статистическими.

Математическое определение вероятности: вероятность какого-либо события – это предел, к которому стремится отношение числа случаев, приводящих к осуществлению события, к общему числу случаев, при бесконечном увеличении последних:
Здесь n′ − число раз, когда событие произошло, а n − общее число опытов. Отсюда следует, что Р может принимать значения от нуля до единицы.

По определению Лапласа, вероятность можно представить как отношение числа благоприятных случаев к числу возможных случаев.

Определить распределение молекул по скоростям вовсе не значит, что нужно определить число молекул, обладающих той, ли иной заданной скоростью. Ибо число молекул, приходящихся на долю каждого значения скорости равно нулю.
Вопрос должен быть поставлен так: «Сколько молекул обладает скоростями, лежащими в интервале, включающем заданную скорость».

Итак, молекулы движутся хаотически. Среди них есть и очень быстрые, и очень медленные. Благодаря беспорядочному движению и случайному характеру их взаимных столкновений, молекулы определённым образом распределяются по скоростям. Это распределение оказывается однозначным и единственно возможным, и не только не противоречит хаотическому движению, но именно им и обусловлено.

Нам необходимо знать: сколько молекул обладает скоростями, лежащими в интервале, включаю-щем заданную скорость?
Так всегда ставятся статистические задачи.
Например: на переписи населения, когда указывается возраст 18 лет – это не значит, что 18 лет, 0 часов, 0 минут. Эта цифра свидетельствует, что возраст лежит в интервале от 18 до 19 лет.

Мы будем искать число частиц (Δn) скорости которых лежат в определённом интервале значения скорости Δυ ( т.е. от υ до ).
Здесь Δn – число благоприятных молекул, попавших в этот интервал.
Очевидно, что в единице объёма число таких благоприятных молекул тем больше, чем больше Δυ.

Ясно так же, что Δn должно быть пропорционально концентрации молекул (n).
Число Δn зависит и от самой скорости, так как в одинаковых по величине интервалах, но при разных абсолютных значениях скорости, число молекул будет различным Смысл сказанного легко понять из простого примера: неодинаково, число людей в возрас-те от 20 до 21 года и от 90 до 91 года.
И так

И так,
Здесь f(υ) – функция распределения молекул по скоростям, n – концентрация молекул и
Δυ - интервал значений скоростей.
Перейдя к пределу, получим
Физический смысл f(υ) в том, что это отно-шение числа молекул, скорости которых лежат в определенном интервале скоростей, к общему числу молекул в единичном интервале скоростей:
(2.2.2)

Таким образом, f(υ) – имеет смысл вероятности, то есть показывает, какова вероятность любой молекулы газа в единице объёма иметь скорость, заключённую в единичном интервале, включающем заданную скорость υ.
В данном случае f(υ) называют плотностью вероятности.

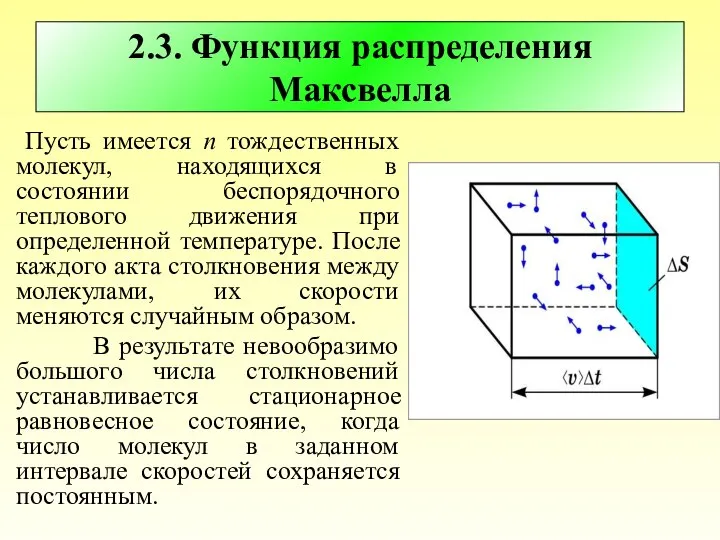
2.3. Функция распределения Максвелла
Пусть имеется n тождественных молекул, находящихся в состоянии беспорядочного теплового движения при определенной температуре. После каждого акта столкновения между молекулами, их скорости меняются случайным образом.
В результате невообразимо большого числа столкновений устанавливается стационарное равновесное состояние, когда число молекул в заданном интервале скоростей сохраняется постоянным.

В результате каждого столкновения проекции скорости молекулы испытывают случайное изменение на Δυx, Δυy, Δυz, причем изменения каждой проекции скорости независимы друг от друга.
Найдем в этих условиях, каково число частиц dn из общего числа n имеет скорость в интервале
от υ до

При этом, мы не можем ничего определенного сказать о точном значении скорости той или иной частицы υi, поскольку за столкновениями и движениями каждой из молекул невозможно проследить ни в опыте, ни в теории. Такая детальная информация вряд ли имела бы практическую ценность.
Распределение молекул идеального газа по скоростям впервые было получено знаменитым английским ученым Дж. Максвеллом в 1860 году с помощью методов теории вероятностей.

Максвелл Джеймс Клерк (1831 – 1879) –
английский физик.
Работы посвящены электродинамике, молекулярной физике, общей статике, оптике, механике, теории упругости. Установил статистический закон, описывающий распределение молекул газа по скоростям.

Вывод формулы функции распределения молекул по скоростям есть в учебнике Ю.И Тюрина. и др.(ч. 1), или И.В. Савельева (т. 1). Мы воспользуемся результатами этого вывода.

Скорость – векторная величина. Для проекции скорости на ось х (x-ой состав-ляющей скорости), имеем
тогда
или

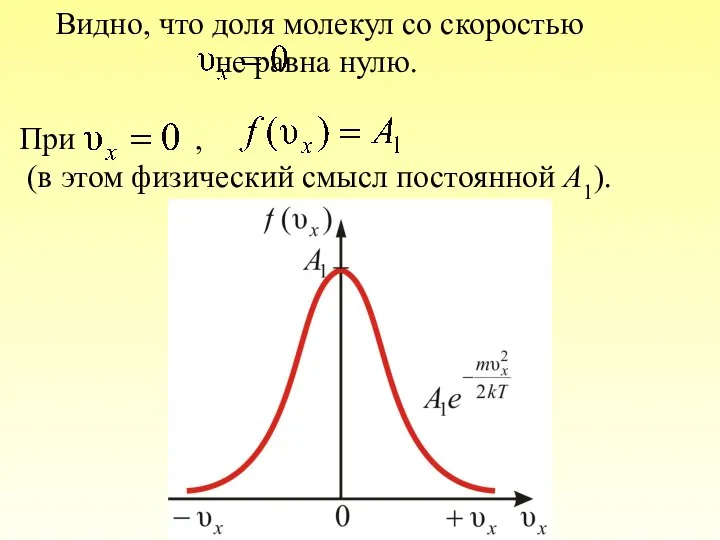
Видно, что доля молекул со скоростью не равна нулю.
При , (в этом физический смысл постоянной А1).

Приведённое выражение и график справедливы для распределения молекул газа по x-ым компонентам скорости. Очевидно, что и по y–ым и z–ым компонентам скорости также можно получить:

Вероятность того, что скорость молекулы одновременно удовлетворяет трём условиям: x – компонента скорости лежит в интервале от υх до ; y – компонента, в интервале от υy до ; z – компонента, в интервале от υz до будет равна произведению вероятностей каждого из условий (событий) в отдельности:
где

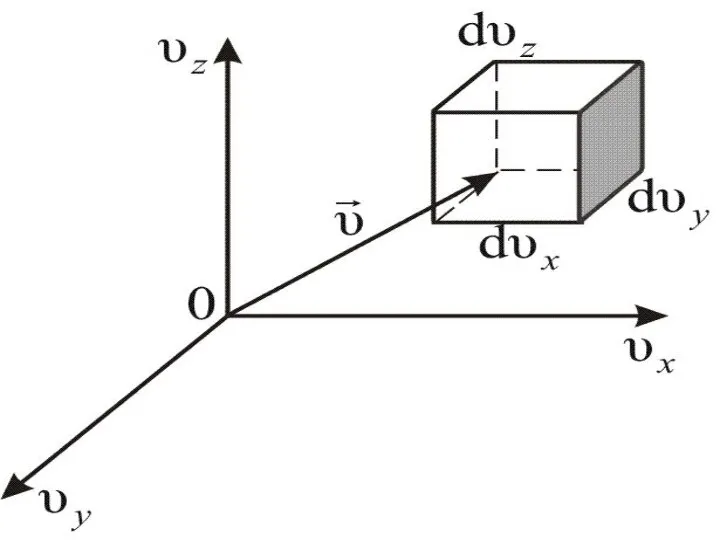
Или
(2.3.2)
Этой формуле можно дать геометрическое истолкование: dnxyz – это число молекул в параллелепипеде со сторонами dυx, dυy, dυz, то есть в объёме (рисунок 2.4), находящемся на расстоянии от начала координат в пространстве скоростей.

Величина (dnxyz) не может зависеть от направления вектора скорости. Поэтому надо получить функцию распределения молекул по скоростям независимо от их направления, то есть по абсолютному значению скорости.
Если собрать вместе все молекулы в единице объёма, скорости которых заключены в интервале от υ до по всем направлениям, и выпустить их, то они окажутся через одну секунду в шаровом слое толщиной dυ и радиусом υ (см. рисунок).

Этот шаровой слой складывается из тех параллелепипедов, о которых говорилось выше.
Объём этого шарового слоя:
Общее число молекул в слое:

Отсюда следует закон Максвелла – распределение молекул по абсолютным значениям скоростей:
(2.3.3)
где – доля всех частиц единичного объёма, скорости которых лежат в интервале от υ до

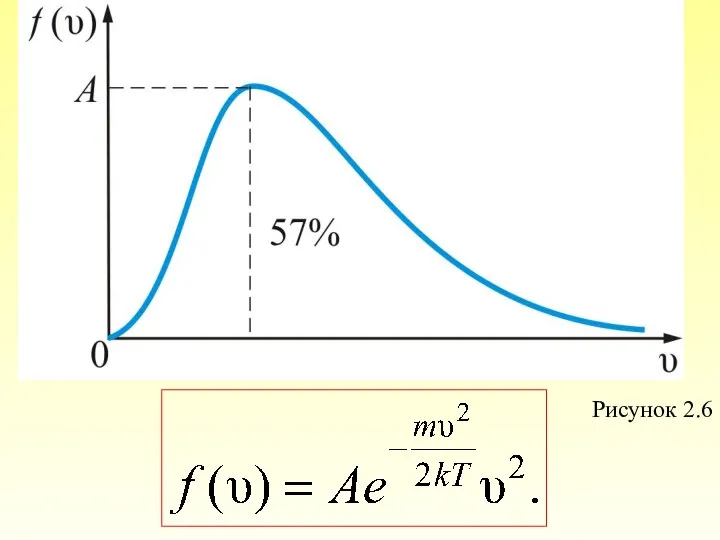
При получаем плотность вероятности, или функцию распределения молекул по скоростям:
(2.3.4)
Эта функция обозначает долю молекул единичного объёма газа, абсолютные скорости которых заключены в единичном интервале скоростей, включающем данную скорость.

Обозначим тогда, из (2.3.4) получим:
(2.3.5)
График этой функции показан на рис. 2.6.

Рисунок 2.6

Выводы:
- Вид распределения молекул газа по скоростям, для каждого газа зависит от рода газа (m) и от параметра состояния (Т). Давление P и объём газа V на распределение молекул не влияют.
- В показателе степени стоит отношение, кинетической энергии, соответствующей данной скорости υ к средней энергии теплового движения молекул при данной температуре:

Значит распределение Максвелла характеризует распределение молекул по значениям кинетической энергии (то есть показывает, какова вероятность при данной температуре иметь именно такое значение кинетической энергии).

Рассмотрим пределы применимости классического описания распределения частиц по скоростям. Для этого воспользуемся соотношением неопределенностей Гейзенберга. Согласно этому соотношению координаты и импульс частицы не могут одновременно иметь определенное значение. Классическое описание возможно, если выполнены условия:

Здесь – фундаментальная константа (постоянная Планка), определяющая масштаб квантовых (микроскопических процессов).
Таким образом, если частица находится в объеме , то в этом случае возможно описание ее движения на основе законов классической механики.

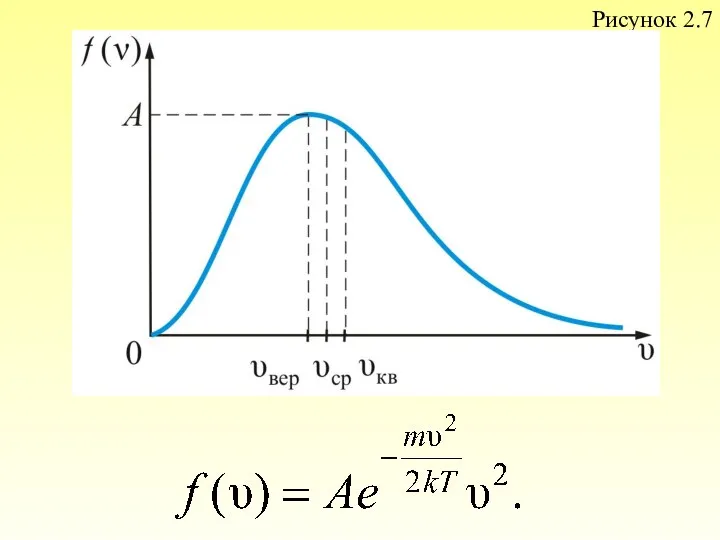
Наиболее вероятная, среднеквадратичная и
средняя арифметическая скорости молекул газа
Рассмотрим, как изменяется с абсолютной величиной скорости число частиц, приходящихся на единичный интервал скоростей, при единичной концентрации частиц.
График функции распределения Максвелла приведен на рис. 2.7.

Рисунок 2.7

Из графика видно, что при «малых» V, т.е. при , имеем ;затем достигает максимума А и далее экспоненциально спадает .

Величина скорости, на которую приходится максимум зависимости называют наиболее вероятной скоростью. Величину этой скорости найдем из условия равенства нулю производной

– наиболее вероятная скорость одной молекулы.
для одного моля газа:

Среднюю квадратичную скорость найдем используя соотношение : – для одной молекулы. (2.3.8)
– для одного моля газа. (2.3.9)

Средняя арифметическая скорость − υср
где – число молекул со скоростью от υ до . Если подставить сюда f(υ) и вычислить, то получим:
– для одной молекулы.
– для одного моля газа.

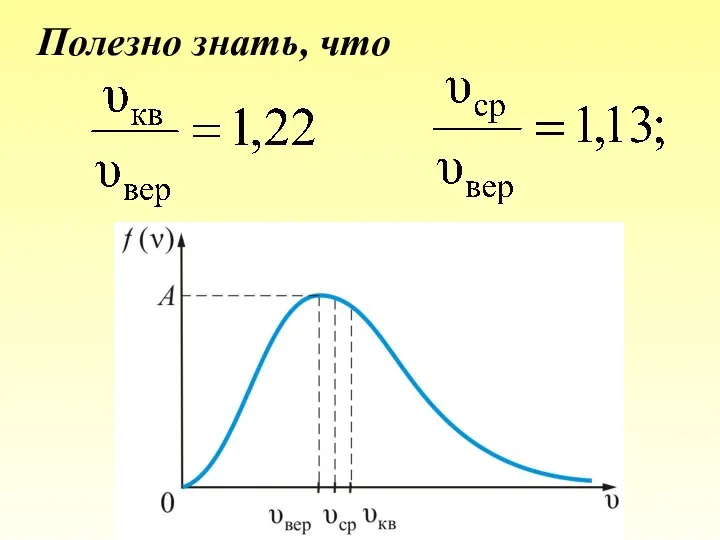
Полезно знать, что

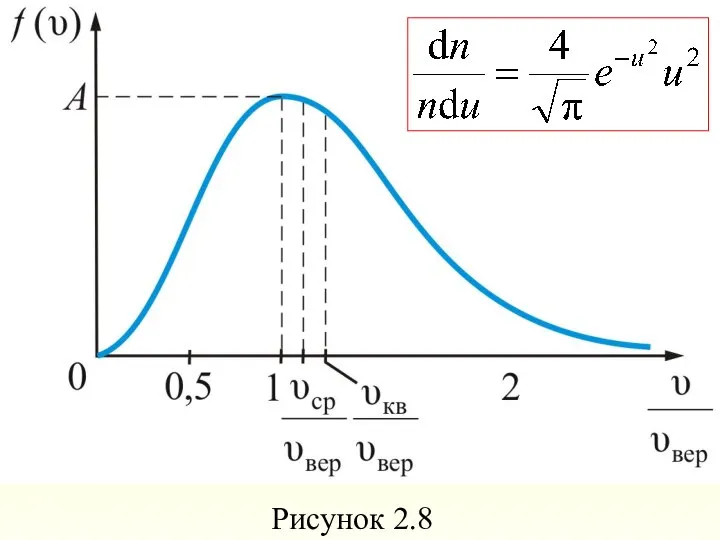
Формула Максвелла для относительных скоростей
Для решения многих задач удобно использовать формулу Максвелла, где скорость выражена в относительных единицах.
Относительную скорость обозначим через u:
(2.3.13)
где

Это уравнение универсальное.
В таком виде функция распределения не зависит ни от рода газа, ни от температуры (рис. 2.8).
Формула Максвелла для относитель-ных скоростей

Рисунок 2.8

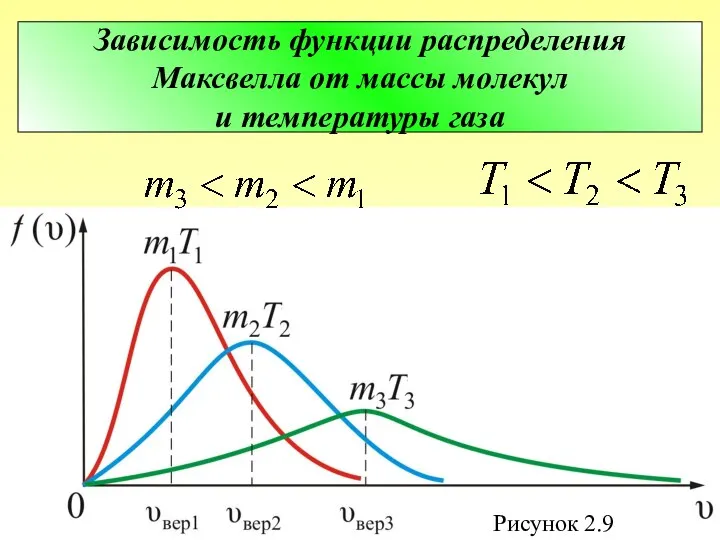
Зависимость функции распределения Максвелла от массы молекул
и температуры газа
Рисунок 2.9

Из рис. 2.9 можно проследить за изменением
при изменении m и T: (при ) или (при ). Площадь под кривой величина постоянная, равная единице ( ), поэтому важно знать как будет изменяться положение максимума кривой:
Максвелловский закон распределения по скоростям и все вытекающие следствия справедливы только для газа в равновесной системе. Закон статистический и выполняется тем лучше, чем больше число молекул.

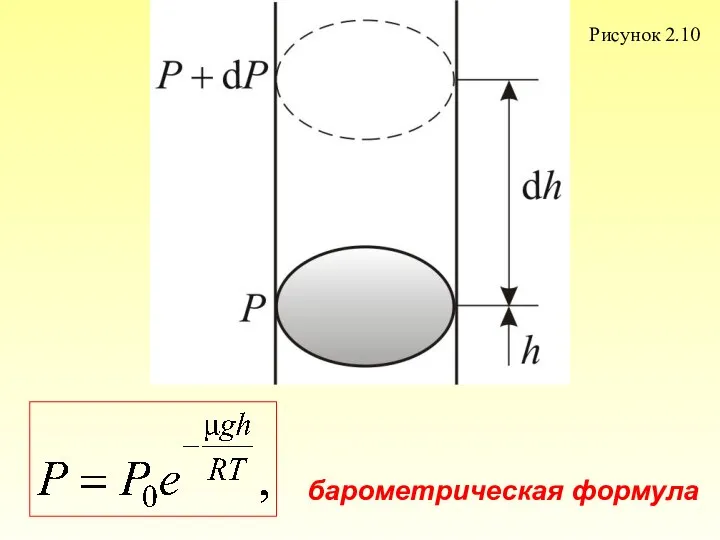
2.4. Барометрическая формула
Рассмотрим ещё один, очень важный закон.
Атмосферное давление на какой-либо высоте h обусловлено весом выше лежащих слоёв газа.
Пусть P – давление на высоте h, а – на высоте
(рисунок 2.10).

Рисунок 2.10
барометрическая формула

Причём , dР < 0, так как на большей высоте давление меньше. Разность давления равна весу газа, заключённого в объёме цилиндра с площадью основания равного единице и высотой dh, ρ − плотность газа на высоте h, медленно убывает с высотой.
Отсюда
(2.4.1)
где P0 – давление на высоте . Это барометрическая формула.

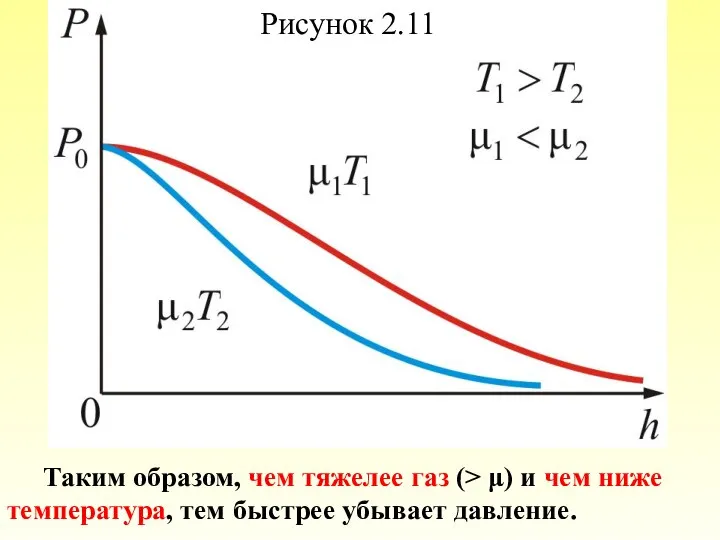
Из барометрической формулы следует, что P убывает с высотой тем быстрее, чем тяжелее газ (чем больше μ) и чем ниже температура (например, на больших высотах концентрация легких газов Не и Н2 гораздо больше чем у поверхности Земли). На рисунке 2.11 изображены две кривые, которые можно трактовать, либо как соответствующие разным μ (при одинаковой Т), либо как отвечающие разным Т, при одинаковых μ.

Рисунок 2.11
Таким образом, чем тяжелее газ (> μ) и чем ниже температура, тем быстрее убывает давление.

2.5. Распределение Больцмана
Распределение Больцмана определяет распределение частиц в силовом поле в условиях теплового равновесия.

Больцман Людвиг (1844 – 1906) – австрийский физик-
теоретик, один из основоположников классической
статистической физики. Основные работы в области кинетической теории газов, термодинамики и теории излучения. Вывел основное кинетическое уравнение газов, являющееся основой физической кинетики. Впервые применил к излучению принципы термодинамики.

Пусть идеальный газ находится в поле консервативных сил, в условиях теплового равновесия. При этом, концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия.
Число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения
тоже убывает.

Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.

Исходя из основного уравнения молекулярно-кинетической теории: , заменим P и P0 в барометрической формуле (2.4.1) на n и n0 и получим распределение Больцмана для молярной массы газа:
(2.5.1)
где n0 и n − число молекул в единичном объёме на высоте h = 0 и h, соответственно.

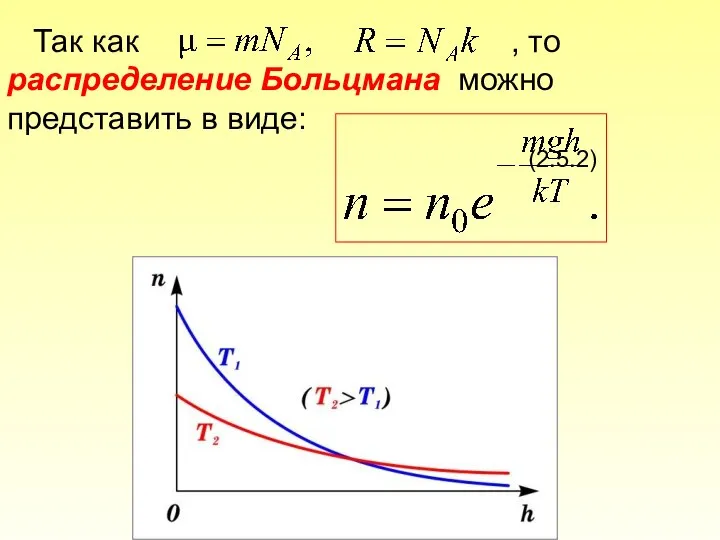
Так как , то распределение Больцмана можно представить в виде:
(2.5.2)

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При тепловое движение прекращается, все молекулы расположились бы на земной поверхности.
При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой.

Так как –потенциальная энергия, следовательно, распределение Больцмана характеризует распределение частиц по значениям потенциальной энергии:
(2.5.3)
– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n0 – число молекул в единице объёма в там, где .

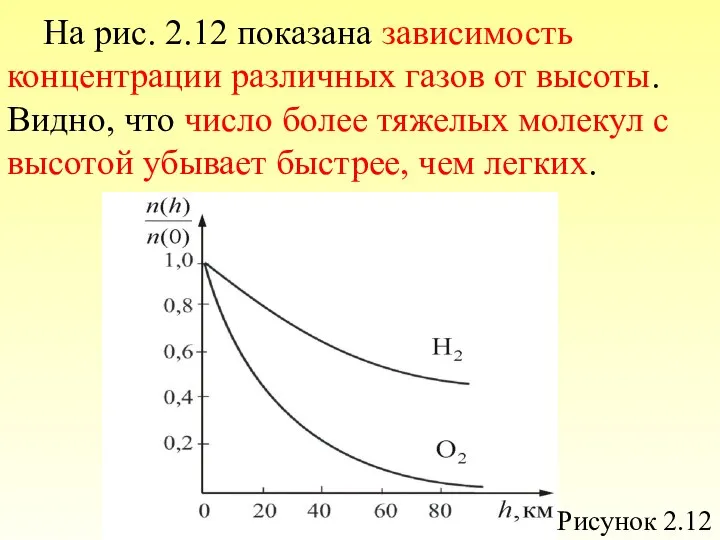
На рис. 2.12 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.
Рисунок 2.12

Из (2.5.3) можно получить, что отношение концентраций молекул в точках с U1 и U2 обладающих именно таким значением
(2.5.4)
Больцман доказал, что соотношение (2.5.3) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном поле, для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.

2.6. Закон распределения Максвелла-Больцмана
В п. 2.3 мы получили выражение для распределения молекул по скоростям (распределение Максвелла):
(2.6.1)

Из этого выражения легко найти распределение молекул газа по значениям кинетической энергии K. Для этого перейдём от переменной υ к переменной :
где dn(K) – число молекул, имеющих кинетическую энергию поступательного движения, заключённую в интервале от K до

Отсюда получим функцию распределения молекул по энергиям теплового движения:
(2.6.2)
Средняя кинетическая энергия молекулы идеального газа:
то есть получили результат, совпадающий с прежним результатом, полученным в п. 1.3.

Итак, закон Максвелла даёт распределение частиц по значениям кинетической энергии а закон Больцмана – распределение частиц по значениям потенциальной энергии. Оба распределения можно объединить в единый закон Максвелла-Больцмана, согласно которому, число молекул в единице объёма, скорости которых лежат в пределах от υ до
равно:
(2.6.3)

Обозначим – полная энергия. Тогда
(2.6.4)
Это и есть закон распределения Максвелла-Больцмана.
Здесь n0 – число молекул в единице объёма в той точке, где ; .

В последнем выражении, потенциальная и кинетическая энергии, а следовательно и полная энергия Е, могут принимать непрерывный ряд значений. Если же энергия частицы может принимать лишь дискретный ряд значений Е1, Е2 ... (как это имеет место, например, для внутренней энергии атома), то в этом случае распределение Больцмана имеет вид:
, (2.6.5)

где Ni – число частиц, находящихся в состоянии с энергией Еi, а А – коэффициент пропорциональности, который должен удовлетворять условию:
где N – полное число частиц в рассматриваемой системе.

Тогда, окончательное выражение распределения Масвелла-Больцмана для случая дискретных значений будет иметь вид: (2.6.6)

2.7. Распределение Бозе-Эйнштейна, Ферми-Дирака
Если у нас имеется термодинамическая система состоящая из N частиц, энергии которых могут принимать дискретные значения , то говорят о системе квантовых чисел.
Поведение такой системы описывается квантовой статистикой, в основе которой лежит принцип неразличимости тождественных частиц.

Основная задача этой статистики состоит в определении среднего числа частиц, находящихся в ячейке фазового пространства: «координаты – проекции импульса» (x, y, z и px, py, pz) частиц.
При этом имеют место два закона распределения частиц по энергиям (две статистики):

распределение Бозе-Эйнштейна:
; (2.7.1)
распределение Ферми-Дирака:
. (2.7.2)

Первая формула описывает квантовые частицы с целым спином (собственный момент количетсва движения). Их называют бозоны (например, фотоны).
Вторая формула описывает квантовые частицы с полуцелым спином. Их называют фермионы (например: электроны, протоны, нейтрино).