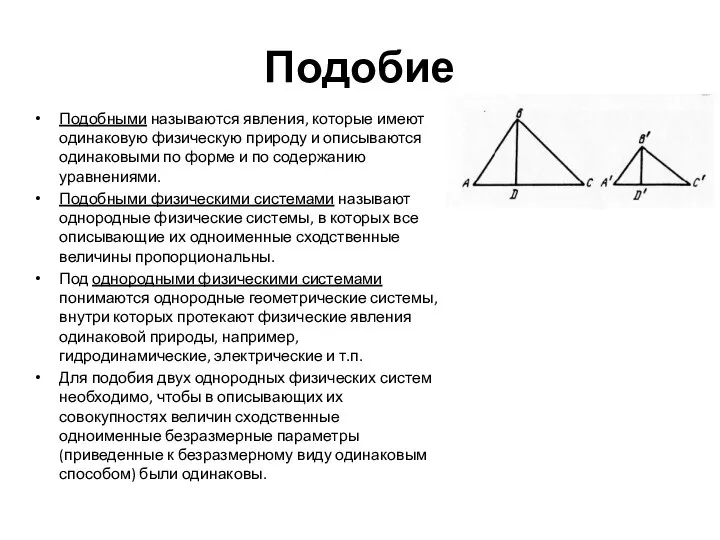
о соотношениях между эффектами и об условиях однозначности в них фактически не разделена, так как каждая из величин, входящих в такие зависимости, выражена в универсальных единицах, т.е. сопоставляется с общепринятыми эталонами (масштабами) .
Содержится информация двух видов:
1) об условиях однозначности, т.е. об области протекания рассматриваемого процесса;
2) о количественных соотношениях между интенсивностями существенных для процесса физических эффектов или величин
Особенностью безразмерных зависимостей является то, что при получении их вместо универсальных масштабов (единиц измерения) величин используются такие, которые являются существенными именно для рассматриваемых процессов. В результате универсальные масштабы (единицы измерения) фактически исключаются из безразмерных зависимостей, а следовательно, исключаются фактически сведения о размере области протекания конкретного процесса.
Остается только один вид информации — информация о количественных соотношениях между действующими физическими эффектами.












 Курс физики. Введение
Курс физики. Введение Расчет и выбор посадок подшипников качения на валы и в отверстия корпусов
Расчет и выбор посадок подшипников качения на валы и в отверстия корпусов Определение отношения удельных теплоемкостей газов методом адиабатического расширения
Определение отношения удельных теплоемкостей газов методом адиабатического расширения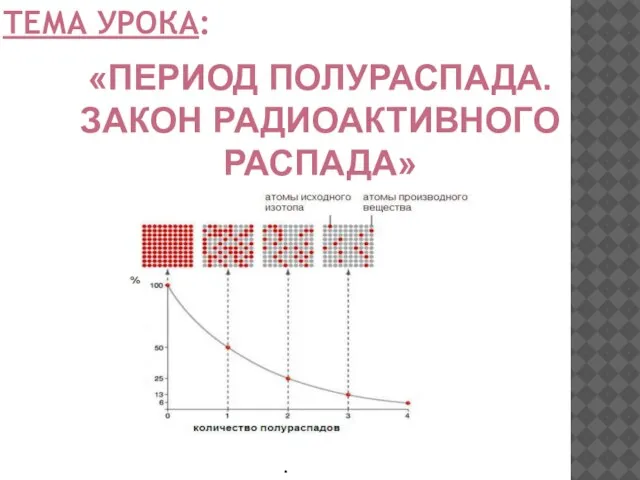 Закон радиоактивного распада
Закон радиоактивного распада Основы конструирования. Базовые навыки работы с наборами
Основы конструирования. Базовые навыки работы с наборами Презентация на тему Работа и энергия
Презентация на тему Работа и энергия  Основные понятия о точности и взаимозаменяемости
Основные понятия о точности и взаимозаменяемости Молекулярно-кинетическая теория. Термодинамика. Задачи
Молекулярно-кинетическая теория. Термодинамика. Задачи Электромагнитные волны
Электромагнитные волны Законы отражения и преломления света
Законы отражения и преломления света Методы определения и единицы измерения влажности воздуха
Методы определения и единицы измерения влажности воздуха Корреляционные лаги
Корреляционные лаги “Жарық техникасы және жарық көздері” пәні бойынша оқу-әдістемелік кешенін жасақтау
“Жарық техникасы және жарық көздері” пәні бойынша оқу-әдістемелік кешенін жасақтау Теоремы статики
Теоремы статики Радио- и СВЧ-волны в средствах связи
Радио- и СВЧ-волны в средствах связи Элементы квантовой физики
Элементы квантовой физики Модуль вектора магнитной индукции. Сила Ампера
Модуль вектора магнитной индукции. Сила Ампера Биология. Физика. Химия. Радиация. Естествознание, 10 класс
Биология. Физика. Химия. Радиация. Естествознание, 10 класс Ремонт генератора
Ремонт генератора Явление электромагнитной индукции
Явление электромагнитной индукции Работа при повороте тела. Кинетическая энергия вращающегося твердого тела
Работа при повороте тела. Кинетическая энергия вращающегося твердого тела Порядок заправки верхней и нижней нити
Порядок заправки верхней и нижней нити Друге суміщення руху робочих органів
Друге суміщення руху робочих органів Пользуйтесь энергосберегающими приборами
Пользуйтесь энергосберегающими приборами Закон сохранения энергии в механике
Закон сохранения энергии в механике Гидроудар. Изэнтропические соотношения в сжимаемых средах. Уравнение баланса. Число Маха и скоростной коэффициент
Гидроудар. Изэнтропические соотношения в сжимаемых средах. Уравнение баланса. Число Маха и скоростной коэффициент "Масса тела. Плотность вещества".
"Масса тела. Плотность вещества". Конвективтік жылуамасудың дербес есептері
Конвективтік жылуамасудың дербес есептері