Пространственная система сил

Студент должен:
иметь представление:
- о пространственных системах сил и их действии на тело.

Знать:
- момент силы относительно оси, свойства момента;
- аналитический способ определения равнодействующей;
-условия равновесия.

Уметь:
-выполнять разложение силы на три взаимно перпендикулярные оси;
-определять момент силы относительно оси;
-определять реакции в опорах и выполнить проверку.

Пространственная
система сил-
система сил, линии действия которых расположены в различных плоскостях.

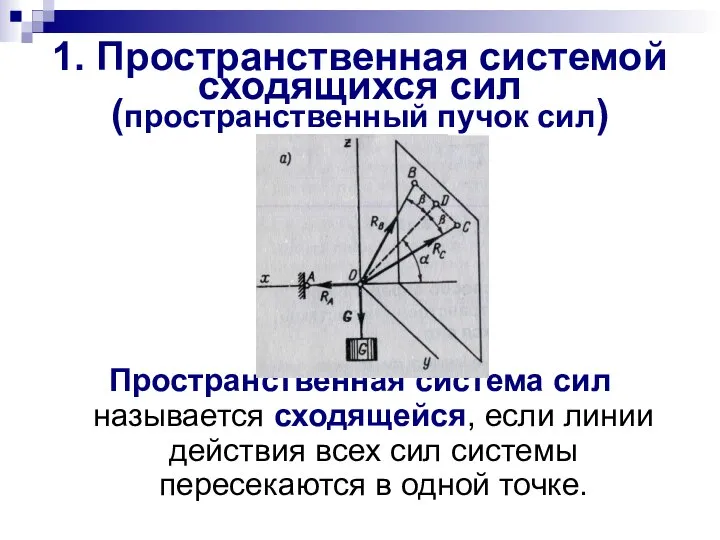
1. Пространственная системой сходящихся сил (пространственный пучок сил)
Пространственная система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Теорема о равнодействующей пространственной ССС.
Пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил системы.
F∑ =∑Fi

Способы определения равнодействующей силы пространственной системы сходящихся сил:
Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей неприемлемы.
Применяется только аналитический способ
( метод проекций).

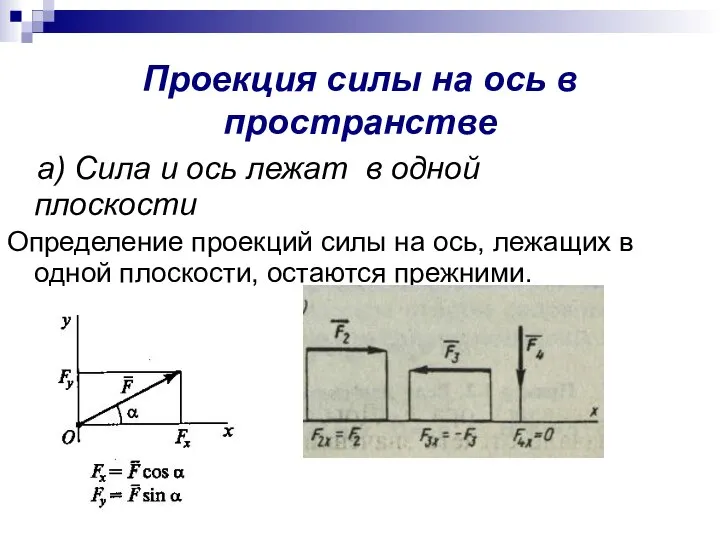
Проекция силы на ось в пространстве
а) Сила и ось лежат в одной плоскости
Определение проекций силы на ось, лежащих в одной плоскости, остаются прежними.

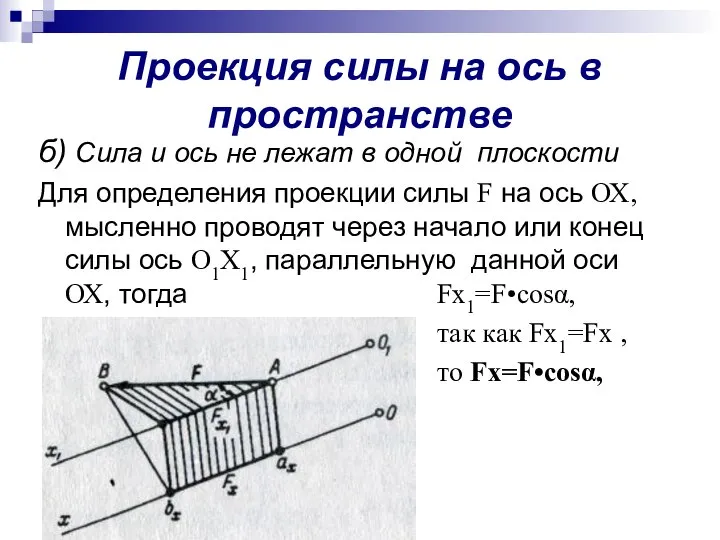
Проекция силы на ось в пространстве
б) Сила и ось не лежат в одной плоскости
Для определения проекции силы F на ось ОХ, мысленно проводят через начало или конец силы ось О1Х1, параллельную данной оси ОХ, тогда Fx1=F•cosα,
так как Fx1=Fx ,
то Fx=F•cosα,

Разложение силы по трём осям координат
Равнодействующая трёх взаимно перпендикулярных сил равна по модулю и направлена по диагонали параллелепипеда, построенного на этих силах.
F=Fx+Fy+Fz

Модуль и направление равнодействующей силы :
- модуль FƩ
FƩ=√Fx2+Fy2+Fz2 =√(∑Xi)2+(∑Yi)2+(∑Zi)2
- направление FƩ
Cos(FƩ,X)=Fx/FƩ=∑Xi/FƩ
Cos(FƩ,Y)=Fy/FƩ= ∑Yi/FƩ
Cos(FƩ,Z)=Fz/FƩ= ∑Zi/FƩ

Аналитическое условие равновесия пространственной ССС
Для равновесия пространственной ССС необходимо и достаточно, чтобы равнодействующая системы, а значит и её проекции на оси координат X,Y и Z были равны 0.
1)∑Fix = ∑Х = 0
FƩ = 0 2)∑Fiy = ∑У = 0
3) ∑Fiz = ∑Z = 0

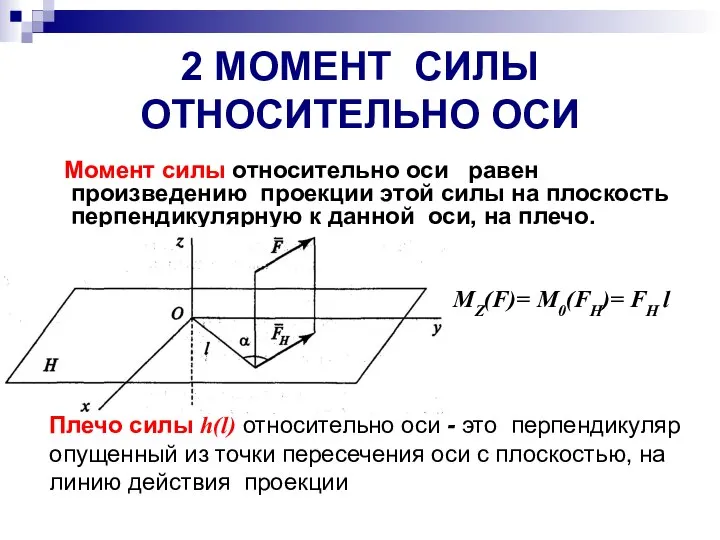
2 МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
Момент силы относительно оси равен произведению проекции этой силы на плоскость перпендикулярную к данной оси, на плечо.
МZ(F)= М0(FH)= FH l
Плечо силы h(l) относительно оси - это перпендикуляр опущенный из точки пересечения оси с плоскостью, на линию действия проекции

Правило знаков
Момент силы относительно оси будем считать положительным , если сила стремится вызвать вращение против часовой стрелки, момент силы считаем отрицательным, если она стремится вызвать вращение по часовой стрелке. При этом необходимо смотреть на плоскость перпендикулярно данной оси с её положительного конца.

Момент силы относительно оси равен нулю в 2 случаях:
1. Если линия действия силы перпендикулярна оси F1⊥Z , т.к. h(l) = 0
2. Если вектор силы параллелен оси
F2//Z , т.к. FH = 0

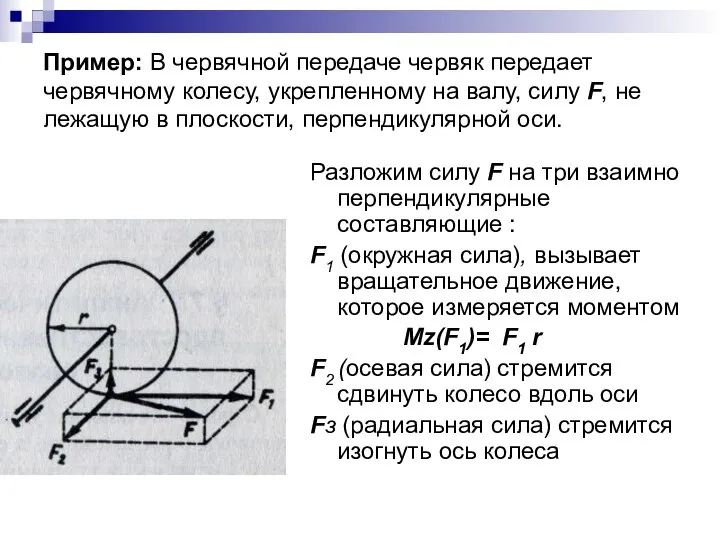
Пример: В червячной передаче червяк передает червячному колесу, укрепленному на валу, силу F, не лежащую в плоскости, перпендикулярной оси.
Разложим силу F на три взаимно перпендикулярные составляющие :
F1 (окружная сила), вызывает вращательное движение, которое измеряется моментом
Мz(F1)= F1 r
F2 (осевая сила) стремится сдвинуть колесо вдоль оси
Fз (радиальная сила) стремится изогнуть ось колеса

3. Пространственная система произвольно расположенных сил -
это система сил, линии действия, которых не лежат в одной плоскости и не пересекаются в одной точке

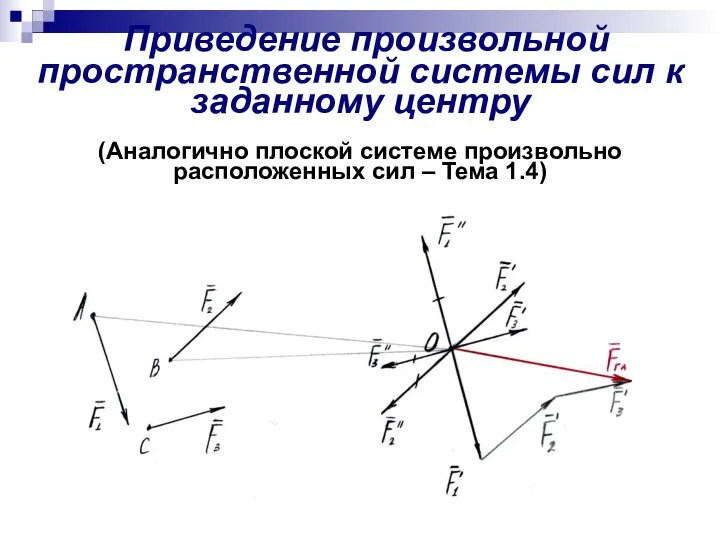
Приведение произвольной пространственной системы сил к заданному центру
(Аналогично плоской системе произвольно расположенных сил – Тема 1.4)

Приведение произвольной пространственной системы сил к заданному центру
Пространственная система произвольно расположенных сил в общем случае эквивалентна одной силе, приложенной в центре приведения и одной паре сил
Произвольная пространственная система сил приводится к главному вектору и главному моменту.

Модуль и направление главного вектора :
- модуль FГЛ
FГЛ=√Fx2+Fy2+Fz2 =√(∑Xi)2+(∑Yi)2+(∑Zi)2
- направление FГЛ
Cos(Fгл; x)= ∑Xi/ Fгл
Cos(Fгл; y)= ∑Yi/ Fгл
Cos(Fгл; z)= ∑Zi/ Fгл

Модуль главного момента :
Алгебраическая сумма моментов всех сил системы относительно каждой оси.
МГЛ = √ (∑МX(Fi))2+(∑МY(Fi))2+ (∑МZ(Fi))2

Аналитические условия равновесия пространственной системы
произвольно расположенных сил
Алгебраическая сумма проекций всех сил на три взаимно перпендикулярные оси координат должна быть равна нулю и алгебраическая сумма моментов всех сил, относительно тех же осей, должна быть равна нулю
1) ∑X=∑ Fi x =0 4) ∑Mx(Fi) =0 Fгл =0 2) ∑Y=∑ Fi y =0 Мгл =0 5)∑My(Fi) =0
3)∑Z=∑ Fi z =0 6)∑Mz(Fi) =0