Проведение прочностных расчетов машин и механизмов на предприятии

О себе
“мы предсказываем будущее” - книга о работе в программном пакете Ansys - инструменте численного моделирования физических процессов через решение дифференциальных уравнений дискретными методами математики

О Вас
интересно предсказывать будущее при помощи численного моделирования
хочется быть частью истории создания технологий термоядерного синтеза
умеете читать
умеете считать
способны к суждению

Задачи инженера-прочниста на предприятии

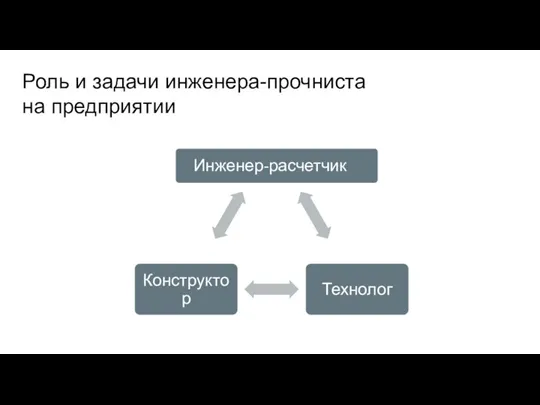
Роль и задачи инженера-прочниста на предприятии

Надежность
Надёжность — свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных условиях применения
Интуитивно надёжность объектов связывают с недопустимостью отказов в работе. Это есть понимание надёжности в «узком» смысле — свойство объекта сохранять работоспособное состояние в течение некоторого времени или некоторой наработки.
Прочность
Жесткость
Устойчивость
Усталость
Ресурс
Долговечность

Надежность
Про́чность (в физике и материаловедении) — свойство материала сопротивляться разрушению под действием напряжений, возникающих под воздействием внешних сил.
Свойство конструкции выполнять назначение, не разрушаясь в течение заданного времени.
Усто́йчивость — способность системы сохранять текущее состояние при влиянии внешних воздействий. Если текущее состояние при этом не сохраняется, то такое состояние называется неустойчивым.
Долгове́чность — свойство элемента или системы длительно сохранять работоспособность до наступления предельного состояния при определенных условиях эксплуатации.
Ресурс (техника) — объём работы или срок эксплуатации, на который рассчитывается машина, здание и т. п. После исчерпания ресурса безопасная работа устройства не гарантируется, ему требуется капитальный ремонт или замена.
Усталость материала — в материаловедении — процесс постепенного накопления повреждений под действием переменных (часто циклических) напряжений, приводящий к изменению свойств материала, образованию трещин, их развитию и разрушению материала за указанное время

Ваши задачи
Жесткость

Современные методы прочностных расчетов

Типы расчетов
Механика сплошной среды: От линейных статических задач
Гидрогазодинамика:
От однофазных потоков
Электромагнетизм:
От низкочастотных завихрений
Системы:
От совместного доступа к данным
До высокоскоростных взаимодействий
До многофазного горения
До расчетов высокочастотных полей
До многодисциплинарных расчетов

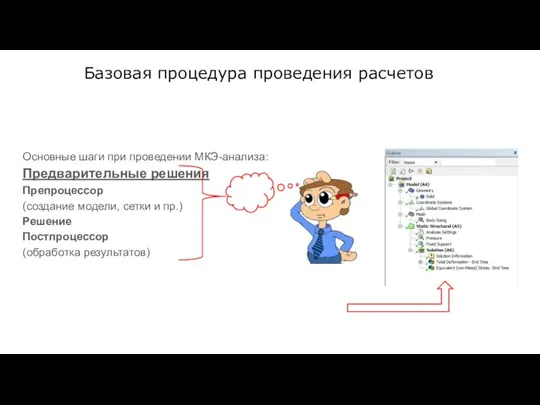
Базовая процедура проведения расчетов
Суть МКЭ-анализа определить отклик конструкции на некоторые нагрузки и граничные условия.
Важно помнить, что МКЭ решение это решение, полученное с применением ряда апроксимаций:
CAD геометрия это идеализация реальной конструкции.
CAE модель это конечноэлементное представление CAD геометрии.
Точность и польза полученных оценок зависит от многих факторов, один из которых густота сетки.

Базовая процедура проведения расчетов
Основные шаги при проведении МКЭ-анализа:
Предварительные решения
Препроцессор
(создание модели, сетки и пр.)
Решение
Постпроцессор
(обработка результатов)

Программное обеспечение для прочностных расчетов

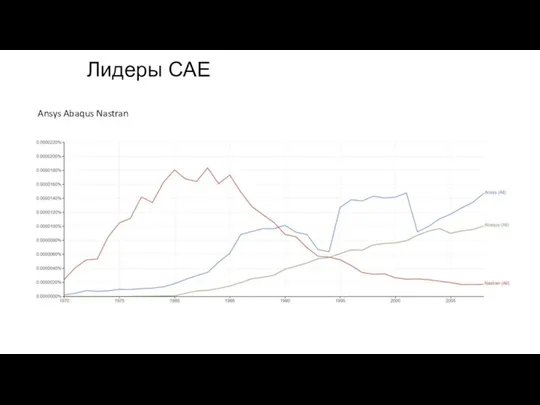
Лидеры CAE
Ansys Abaqus Nastran

Универсальная программная система конечно-элементного анализа ANSYS

Возможности расчетных модулей
Механика сплошной среды: От линейных статических задач
Гидрогазодинамика:
От однофазных потоков
Электромагнетизм:
От низкочастотных завихрений
Системы:
От совместного доступа к данным
До высокоскоростных взаимодействий
До многофазного горения
До расчетов высокочастотных полей
До многодисциплинарных расчетов

Обзор ANSYS Mechanical
В ANSYS Mechanical доступны следующие типы модулей:
Structural Static (Линейная и нелинейная статика)
Structural Dynamic
Modal (модальный анализ)
Harmonic (гармонический анализ)
Response Spectrum (спектральный отклик)
Random Vibration (случайные вибрации)
Transient (линейная и нелинейная динамика)
Rigid dynamics (динамика твердых тел)
Thermal (стационарный и нестационарный тепловой расчет)
Magnetostatic (расчет магнитных полей)
Electrical (расчет электрических полей)
Multiphysics (многодисциплинарный)

Препроцессинг

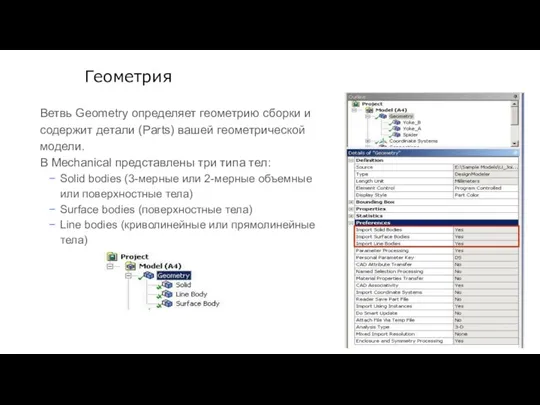
Геометрия
Ветвь Geometry определяет геометрию сборки и содержит детали (Parts) вашей геометрической модели.
В Mechanical представлены три типа тел:
Solid bodies (3-мерные или 2-мерные объемные или поверхностные тела)
Surface bodies (поверхностные тела)
Line bodies (криволинейные или прямолинейные тела)

Геометрия
Твердые тела (Solid bodies) могут быть 2-мерными или 3-хмерными:
По умолчанию 3-мерные тела разбиваются тетраэдрическими или гексаэдрическими конечными элементами высокого порядка с квадратичными функциями формы.
Каждый узел в 3-мерном элементе имеет 3 поступательных степени свободы (перемещения по 3 осям системы координат) для механических расчетов и одну температурную степень свободы (температура) для тепловых.

Плоские задачи
2-мерные твердые тела разбиваются по умолчанию треугольными или четырехугольными элементами высокого порядка с квадратичными функциями формы. Примечание: двумерность расчета устанавливается в настройках проекта до импорта геометрии.
Каждый узел двумерного элемента имеет 2 поступательные степени свободы (перемещения Ux и Uy) в механическом анализе и 1 температурную степень свободы в тепловом.
2-мерные сплошные тела используются для моделирования трех типов трехмерной геометрии, таких как: «Осесимметрия», «Плоское напряженное состояние», «Плоское деформированное состояние».

Балки и оболочки
Поверхностные тела:
Имеют 1 размер, который существенно меньше двух других (толщина стенки). Моделируются такие тела путем задания срединной поверхности и толщины.
Разбиваются на оболочечные конечные элементы, узлы которых имеют по 6 степеней свободы (Ux, Uy, Uz, ROTx, ROTy, ROTz).
Линейные тела:
Имеют 2 размера, которые существенно меньше третьего. Моделируются такие тела путем задания линии (2D/3D) и параметров поперечного сечения. Линейные тела разбиваются на балочные элементы, узлы которых имеют 6 степеней свободы (Ux, Uy, Uz, ROTx, ROTy, ROTz).

Конформная сетка
С точки зрения CAD геометрии тела (bodies) и детали (parts) – одно и то же. В CAD детали объединяются в сборки (Assemblies). Однако, в DesignModeler понятия сборки нет – несколько тел могут быть сгруппированы в многотельные детали (multibody parts).
Несмотря на то, что к каждому телу можно обратиться отдельно и задать свой материал, тела в многотельных деталях имеют общие поверхности, а узлы сеток конечных элементов на контактирующих поверхностях – общие.
(!) В этой ситуации не нужно определять контактное взаимодействие между телами, они действуют как одно целое с общей сеткой конечных элементов – конформной сеткой.
Пример:
На примыкающих поверхностях создаются общие узлы

Свойства материалов
Для проведения линейного статического прочностного расчета требуется определение модуля Юнга и коэффициента Пуассона :
Плотность требуется указать только в случае приложения любых инерционных нагрузок.
Коэффициент теплового расширения требуется задать при приложении температурных нагрузок.
Теплопроводность НЕ требуется при равномерно распределенных температурных условиях.
Пределы прочности нужны только в случае использования при обработке результатов инструмента Stress Tool.
Усталостные свойства необходимы если при постпроцессинге используется инструмент Fatigue Tool.
Требуется дополнительная лицензия на Fatigue Module.
Как было показано ранее материал детали назначается в окне «details» в Mechanical. Пользователь может назначить материал из списка доступных в проекте материалов.

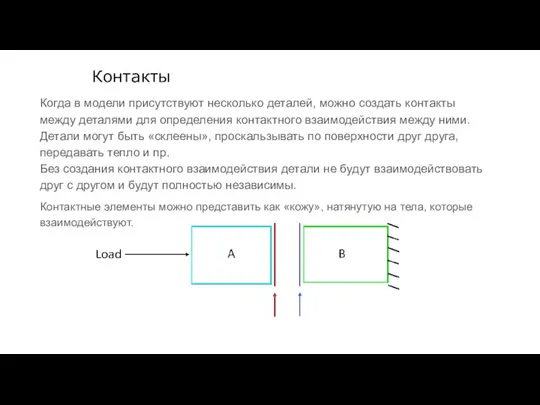
Контакты
Когда в модели присутствуют несколько деталей, можно создать контакты между деталями для определения контактного взаимодействия между ними. Детали могут быть «склеены», проскальзывать по поверхности друг друга, передавать тепло и пр.
Без создания контактного взаимодействия детали не будут взаимодействовать друг с другом и будут полностью независимы.
Контактные элементы можно представить как «кожу», натянутую на тела, которые взаимодействуют.

Контакт
Поверхностные контактные элементы в Mechanical можно представить как «кожу», натянутую на поверхности тел в сборке.
Именно эти элементы определяют поведение конструкции, когда происходит контакт некоторых ее частей (в т.ч. трение, связывание, теплоперенос и т.д.).
В Mechanical элементы контактных пар показаны различными цветами.

Точечные массы
Ветвь Geometry может содержать точечные массы (Point Mass), которые, например, могут быть идеализированным представлением части конструкции не моделируемой непосредственно:
Точечные массы подвержены воздействию инерционных нагрузок (например, “Acceleration,” “Standard Earth Gravity,” “Rotational Velocity”).

Контакты или опоры?
Контакты используются для определения взаимодействия между двумя моделируемыми телами (деталями) в сборке.
Опоры используются для моделирования взаимодействия между телом (деталью) сборки и немоделируемыми объектами (например, «земля», основание агрегата и т.д.)
Опоры определяют взаимодействие с «землей»/основанием
Контакты определяют взаимодействие между частями сборки

Типы элементов

Виды прочностных расчетов

Виды расчетов
Structural Static (Линейная и нелинейная статика)
Structural Dynamic
Modal (модальный анализ)
Harmonic (гармонический анализ)
Response Spectrum (спектральный отклик)
Random Vibration (случайные вибрации)
Transient (линейная и нелинейная динамика)
Rigid dynamics (динамика твердых тел)
Thermal (стационарный и нестационарный тепловой расчет)
Magnetostatic (расчет магнитных полей)
Electrical (расчет электрических полей)
Multiphysics (многодисциплинарный)

Расчет статической прочности

Основы линейного статического расчета
При линейном статическом прочностном расчете вектор перемещений узлов {x} определяется из матричного уравнения:
Допущения:
[K] – постоянная матрица
Применяется линейное упругое поведение материала
Используется теория малых перемещений
{F} – вектор приложенных нагрузок
Подразумевается отсутствие какой-либо зависимости сил от времени
Отсутствует всякое демпфирование в системе
Важно помнить эти допущения в отношении линейного статического расчета.

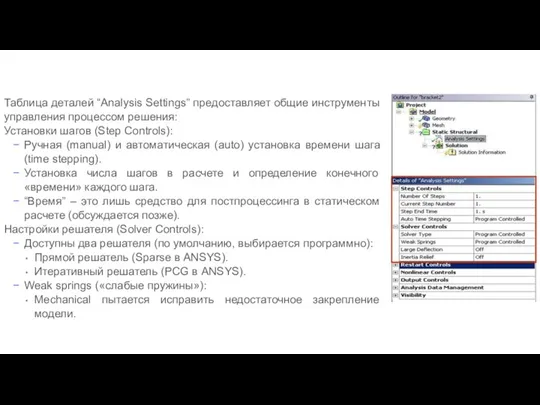
Установки расчета
Таблица деталей “Analysis Settings” предоставляет общие инструменты управления процессом решения:
Установки шагов (Step Controls):
Ручная (manual) и автоматическая (auto) установка времени шага (time stepping).
Установка числа шагов в расчете и определение конечного «времени» каждого шага.
“Время” – это лишь средство для постпроцессинга в статическом расчете (обсуждается позже).
Настройки решателя (Solver Controls):
Доступны два решателя (по умолчанию, выбирается программно):
Прямой решатель (Sparse в ANSYS).
Итеративный решатель (PCG в ANSYS).
Weak springs («слабые пружины»):
Mechanical пытается исправить недостаточное закрепление модели.

Нагрузки
Нагрузки и граничные условия понимаются в контексте степеней свободы (DOF) для используемых элементов.
Для нагрузок и граничных условий на твердые тела доступны три линейных DOF: x, y и z translations (для оболочечных и балочных тел добавляются три вращательных степени свободы rotx, roty и rotz).
Граничные условия, независимо от их названия и типа, всегда определяются для этих DOF.
Граничные условия могут быть приложены на элементы геометрии или к узлам (в зависимости от типа нагрузки).
Граничные условия, прикладываемые непосредственно к узлам, описаны во второй части этого курса.
Пример: “Frictionless Support”, приложенное к поверхности тела справа на рисунке, означает, что Z-координата ограничена, а все другие DOF свободны.

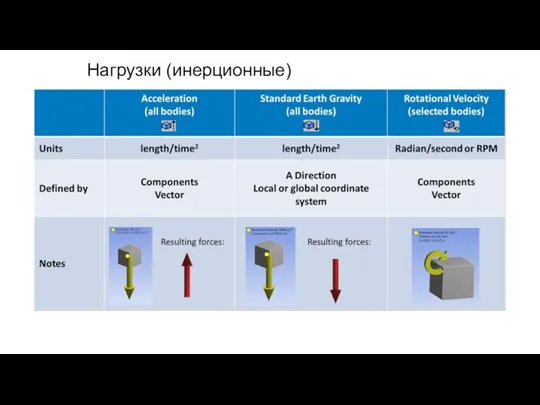
Нагрузки (инерционные)

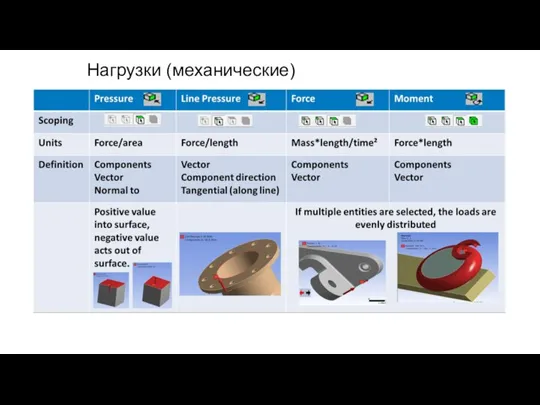
Нагрузки (механические)

Нагрузки
Удаленная сила :
Прикладывает смещенную силу на вершину, кромку, поверхность или узлы.
Пользователь указывает точку приложения силы (выбирая элемент геометрии или задавая координаты).
Может быть определена вектором или по координатам.
Прикладывает эквивалентную силу и момент на поверхность.
Пример: 10” балка с удаленной силой 1 lbf, приложенной на конце балки. Точка приложения силы расположена в 20” от заделки.
20”
F=1 lbf
Moment Reaction

Нагрузки
Предзатяжка болта:
Прикладывается нагрузка от предварительной затяжки болта на цилиндрическую твердотельную поверхность или балку, используя:
Усилия предварительной затяжки (сила)
Затяжка (длина)
Для приложения нагрузки к телу требуется локальная система координат (преднагружение по оси z).
При выборе поверхности используется осевое направление цилиндра

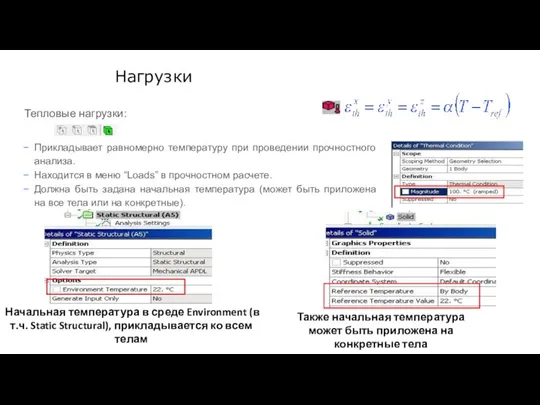
Нагрузки
Тепловые нагрузки:
Прикладывает равномерно температуру при проведении прочностного анализа.
Находится в меню “Loads” в прочностном расчете.
Должна быть задана начальная температура (может быть приложена на все тела или на конкретные).
Начальная температура в среде Environment (в т.ч. Static Structural), прикладывается ко всем телам
Также начальная температура может быть приложена на конкретные тела

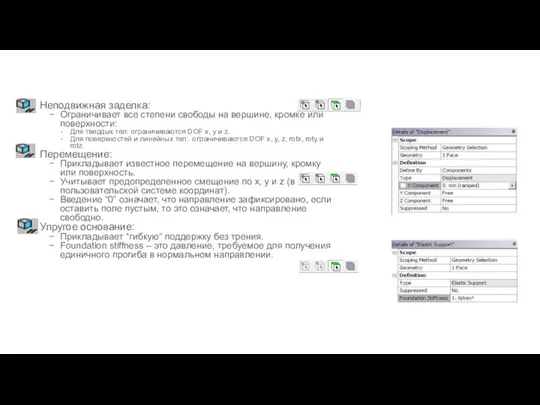
Граничные условия
Неподвижная заделка:
Ограничивает все степени свободы на вершине, кромке или поверхности:
Для твердых тел: ограничиваются DOF x, y и z.
Для поверхностей и линейных тел: ограничиваются DOF x, y, z, rotx, roty и rotz.
Перемещение:
Прикладывает известное перемещение на вершину, кромку или поверхность.
Учитывает предопределенное смещение по x, y и z (в пользовательской системе координат).
Введение “0” означает, что направление зафиксировано, если оставить поле пустым, то это означает, что направление свободно.
Упругое основание:
Прикладывает “гибкую” поддержку без трения.
Foundation stiffness – это давление, требуемое для получения единичного прогиба в нормальном направлении.

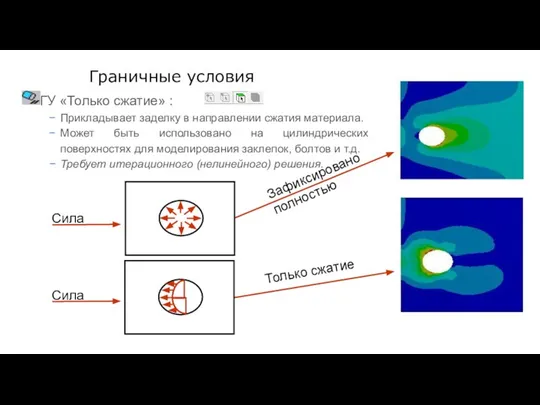
Граничные условия
ГУ «Только сжатие» :
Прикладывает заделку в направлении сжатия материала.
Может быть использовано на цилиндрических поверхностях для моделирования заклепок, болтов и т.д.
Требует итерационного (нелинейного) решения.
Зафиксировано
полностью
Только сжатие
Сила
Сила

KT
LINEAR
NON LINEAR
Линейное и нелинейное решение
В линейном анализе матричное уравнение [K]{x}={F} решается в одну итерацию. Это означает, что жесткость конструкции не изменяется во время решения, т.е. матрица [K] - константа.
В нелинейном решении жесткость может меняться в ходе решения, поэтому используется итерационный процесс для решения задачи. В статическом расчете ANSYS использует нелинейное решение автоматически, если в модели присутствует:
Нелинейное поведение материала: пластичность, ползучесть, прокладки, вязкоупругость, и др.
Нелинейный контакт типа Frictionless, Rough, Frictional.
Возможность больших перемещений.
Опора типа Compression-only.
Шарниры.
Преднатяжение резьбовых компонент.
Пружина типа Compression only или tension only.

Модальный анализ

Теория и допущения

Теория и допущения

Теория и допущения
Итак, при модальном анализе собственные частоты ωi и формы колебаний φi определяются из уравнения:
Допущения:
[K] и [M] – постоянные матрицы:
Принимается линейное упругое поведение материалов
Используется теория малых перемещений и все нелинейности исключаются
Матрица демпфирования [C] отсутствует в расчете
Всякое возмущение на конструкцию отсутствует, вектора нагрузок {F} в уравнении нет
Конструкция может быть как закрепленной, так и незакрепленной
Формы колебаний {φ} имеют относительные, а не абсолютные величины.

Результаты модального расчета
Результаты модального анализа:
Поскольку к модели не приложено никакого возмущения, значения прогибов каждой формы колебаний имеют относительный характер.
Формы колебаний определяются относительно массы компонентов модели.
То же самое касается для других результатов (напряжений, деформаций и т.д.).
Поскольку результаты модального расчета базируются на свойствах модели, а не на конкретном возмущении, их можно интерпретировать только как демонстрацию того, где будет максимум и минимум прогибов при колебаниях на данной частоте, но не как реальные значения этих величин.

Геометрия и свойства материалов
В модальном анализе может быть использована геометрия любого типа:
Твердые, поверхностные и линейные тела.
Можно подключать точечные массы: подключение точечной массы (point mass) добавляет массу конструкции без снижения жесткости, снижая тем самым собственные частоты (K/M)1/2.
Свойства материалов: требуется задание модуля Юнга, коэффициента Пуассона и плотности.
Прочностные и тепловые нагрузки не доступны при модальном анализе:
При полном или частичном отсутствии закреплений появляются нулевые собственные частоты означающие колебания конструкции как единого целого на частотах, равных или близких к 0 Гц.
Выбор граничных условий влияет на форму колебаний и их частоту. Внимательнее относитесь к закреплению модели.

При анализе собственных частот возможно задание контактных областей. Однако, поведение нелинейных типов контакта будет отличаться:
Все контакты будут действовать либо как связанные (bonded) или контакты без разделения (no separation):
При наличии зазора:
Нелинейные типы контактов станут свободными (никакого контакта).
Поведение контактов Bonded и no separation будет зависеть от установок размера области определения pinball.
Контакты

Модальный анализ с преднапряжением
Много примеров вибрации в преднапряженных конструкциях можно найти в музыкальных инструментах (струны гитары, барабанные установки и т.д.). Есть примеры и в инженерных расчетах, когда неучет предварительного напряжения может стать критическим.
Примечание: при предварительном растяжении собственные частоты конструкции увеличиваются, при предварительном сжатии – уменьшаются.

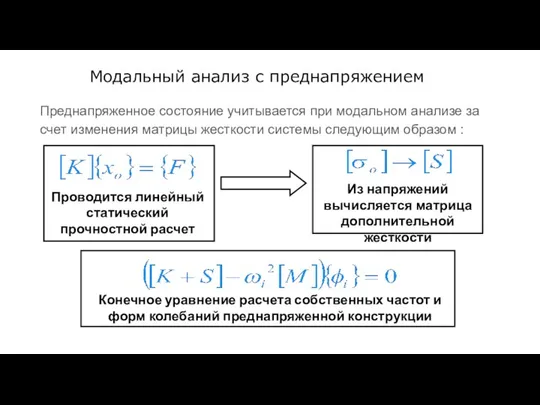
Модальный анализ с преднапряжением
Преднапряженное состояние учитывается при модальном анализе за счет изменения матрицы жесткости системы следующим образом :
Из напряжений вычисляется матрица дополнительной жесткости

Расчет усталостной прочности

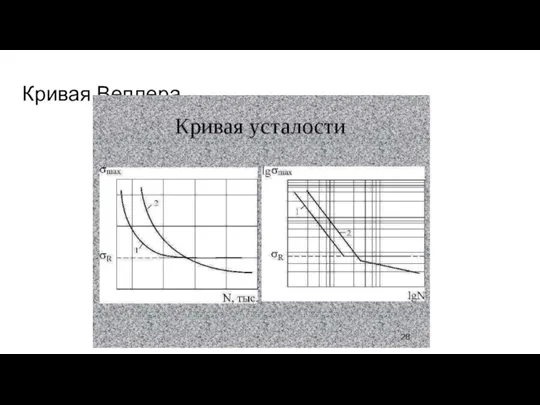
Кривая Веллера

Предел усталости

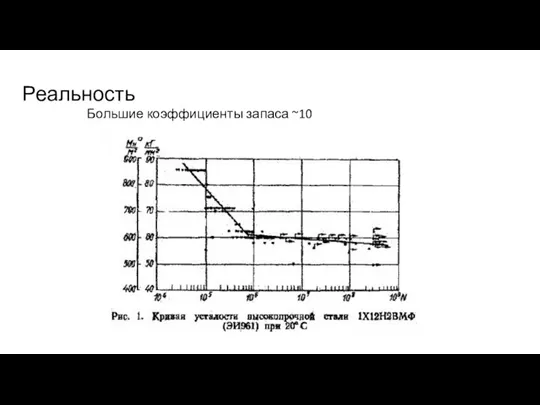
Реальность
Большие коэффициенты запаса ~10

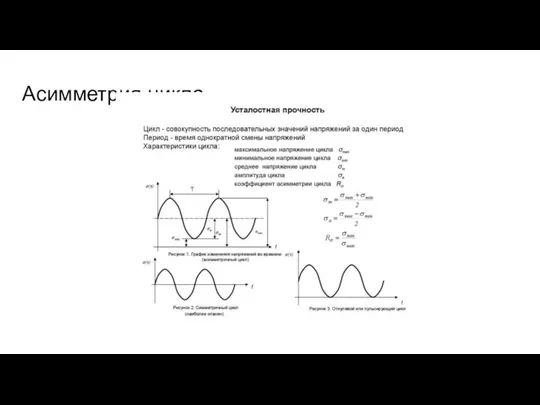
Асимметрия цикла

Правило Майнера

Правило Майнера

Тепловой и термомеханический расчет

Стационарный тепловой расчет
В стационарном тепловом расчете в Mechanical вектор узловых температур {T} определяется из матричного уравнения:
Допущения:
Все нестационарные явления исключаются при проведении стационарного расчета
Матрица [K] может быть постоянной или являться функцией температуры
Вектор {Q} может быть постоянным или являться функцией температуры
Заданные температуры являются граничными условиями {T} в системе (подобно заданным перемещениям в прочностном расчете).
Важно помнить эти допущения при проведении тепловых расчетов в ANSYS Mechanical.

Стационарный тепловой расчет
Температурно-прочностная аналогия

Контакты
По умолчанию применяется абсолютный тепловой контакт, означающий отсутствие падения температуры при теплопередаче от одной поверхности к другой.
Многочисленные “реальные” условия ведут к тому, что проводимость реального теплового контакта отличается от абсолютной:
Шероховатость поверхности
Отделка поверхности
Оксидные пленки
Смоченность поверхности жидкостями
Контактное давление
Поверхностная температура
Смазки
И т.д. . . . .

Граничные условия
Тепловой поток:
Тепловой поток может быть приложен к вершине, кромке или поверхности.
Имеет размерность Энергия/время.
Удельный тепловой поток :
Может быть приложен только к поверхностям (к кромкам при 2D-расчете).
Имеет размерность Энергия/время/площадь.
Внутренний источник тепла:
Может быть задан только для твердых тел.
Имеет размерность Энергия/время/объем.
Положительные значения тепловой нагрузки соответствуют подведению энергии к модели.

Граничные условия
Температура, Конвекция и Излучение:
Как минимум одно условие, содержащее температуру {T} должно присутствовать в модели, чтобы исключить тривиальность решения задачи (предотвратить температурный аналог недозакрепленности модели).
Температура:
Определение заданной температуры на вершинах, кромках, поверхностях или телах.
Конвекция:
Задается дополнительно
температура окружающей среды
Radiation:
Задается дополнительно
температура окружающей среды

Результаты теплового расчета
Для просмотра доступны различные результаты:
Температуры
Удельные тепловые потоки (Heat Flux)
Реактивные тепловые потоки (“Reaction” Heat Flow Rate)
Пользовательские результаты
В Mechanical результаты могут быть запрошены как до решения, так и после него.
Снова решать задачу не нужно, все возможные результаты уже сохранены в файл, нужно их запросить.

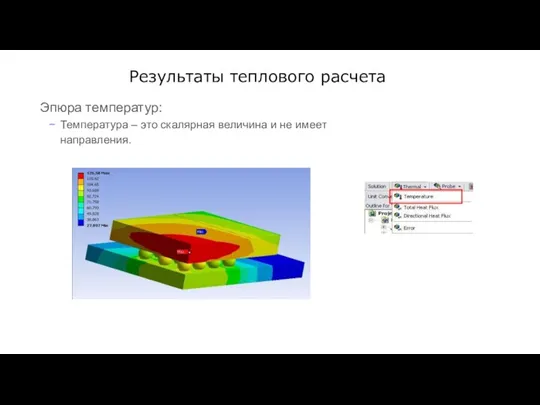
Результаты теплового расчета
Эпюра температур:
Температура – это скалярная величина и не имеет направления.

Результаты теплового расчета
Можно построить эпюры и векторные поля удельных тепловых потоков:
Удельный тепловой поток q определяется по формуле:
Можно построить общий “Total Heat Flux” и направленный “Directional Heat Flux” тепловые потоки
Амплитуду и направление можно изобразить векторами при переходе в векторный режим отображения результатов.

Оценка устойчивости

Множество конструкций предполагают оценку их устойчивости. При расчетах тонких труб под сжимающей нагрузкой, сосудов под вакуумом и других подобных конструкций нельзя не учитывать вопросы устойчивости.
Неустойчивость конструкции может быть глобальной (потеря устойчивости) или локальной (локальное течение или потеря устойчивости от сосредоточенной нагрузки).
Проблемы неустойчивости обычно приводят к трудностям сходимости и поэтому требуют применения специальных нелинейных подходов.
Понятие устойчивости

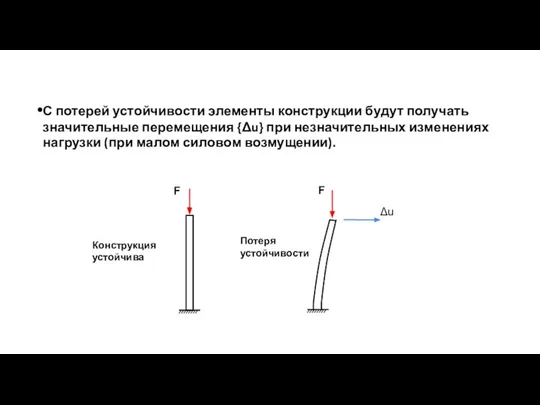
С потерей устойчивости элементы конструкции будут получать значительные перемещения {Δu} при незначительных изменениях нагрузки (при малом силовом возмущении).
Понятие устойчивости

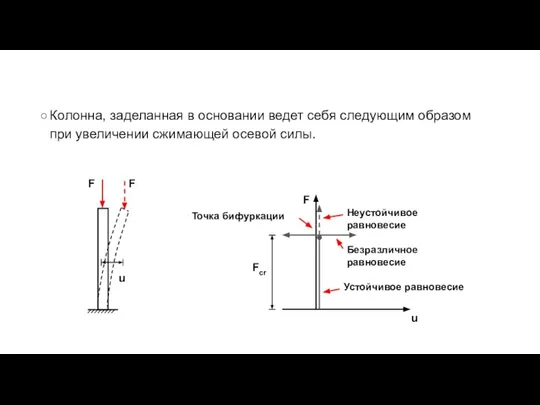
Колонна, заделанная в основании ведет себя следующим образом при увеличении сжимающей осевой силы.
Понятие устойчивости

Точка бифуркации
Это точка в истории нагружения после которой возможны две ветви развития.
В случае сжатой колонны при достижении критической силы (Fcr), колонна может изогнуться влево или вправо. Оба варианта (пути) развития возможны. В случае реальной конструкции существующие геометрические отклонения от идеала или незначительное дополнительное воздействие (P ≠ 0) будет определять направление изгиба.
Понятие устойчивости

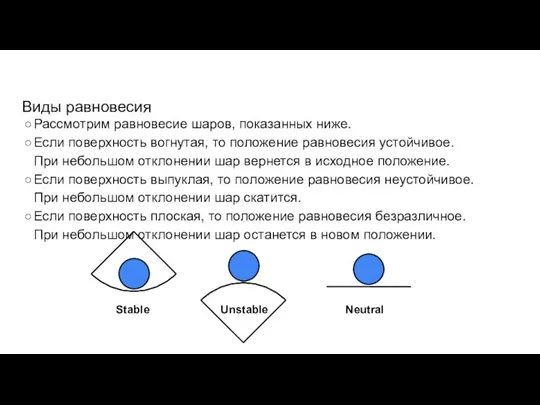
Виды равновесия
Рассмотрим равновесие шаров, показанных ниже.
Если поверхность вогнутая, то положение равновесия устойчивое. При небольшом отклонении шар вернется в исходное положение.
Если поверхность выпуклая, то положение равновесия неустойчивое. При небольшом отклонении шар скатится.
Если поверхность плоская, то положение равновесия безразличное. При небольшом отклонении шар останется в новом положении.
Понятие устойчивости

Критическая нагрузка
При силе F меньше критической силы Fcr колонна находится в состоянии устойчивого равновесия. Если приложить малую возмущающую силу (P ≠ 0), а потом убрать ее, колонна вернется в исходное положение.
При F > Fcr колонна находится в неустойчивом положении равновесия. Любая возмущающая сила вызовет мгновенный изгиб колонны, а при дальнейшем отсутствии возмущающей силы, колонна НЕ вернется в исходное положение.
При F = Fcr колонна находится в безразличном положении равновесия. Так определяется критическая нагрузка.
Понятие устойчивости

Предельная нагрузка
В реальных конструкциях критическая нагрузка почти никогда не достижима.
Обычно конструкция становится нестабильной еще до критической величины нагрузки.
Это происходит из-за нелинейного поведения и не идеальности конструкции.
Понятие устойчивости

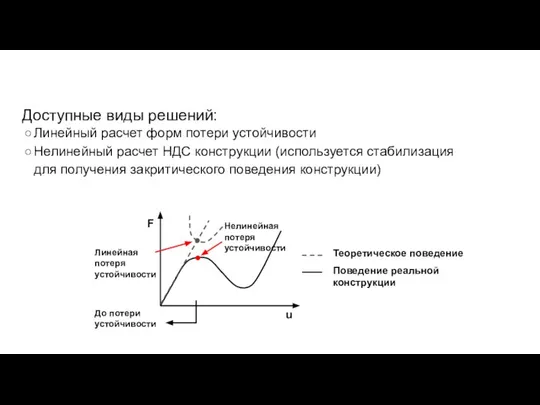
Доступные виды решений:
Линейный расчет форм потери устойчивости
Нелинейный расчет НДС конструкции (используется стабилизация для получения закритического поведения конструкции)
F
u
Теоретическое поведение
Поведение реальной конструкции
До потери устойчивости
Линейная потеря устойчивости
Нелинейная потеря устойчивости
Понятие устойчивости

Ниже показан пример нелинейной кривой прогибов в некоторой конструкции. На диаграмме показаны идеализированная кривая нагрузки, неидеализированная кривая и кривая из эксперимента.
Нелинейный анализ устойчивости

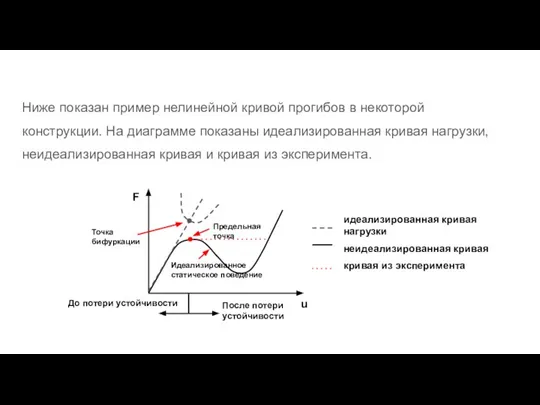
О линейном анализе устойчивости
Линейный анализ устойчивости или анализ устойчивости с помощью собственных значений (Eigenvalue or linear buckling analysis) предсказывает теоретическое значение нагрузок, вызывающих потерю устойчивости для идеальных упругих линейных моделей.
Этот метод соответствует подходу, описанному в курсах устойчивости упругих систем: например, собственное значение при расчете устойчивости колонны соответствует классическому решению Эйлера.
Однако, погрешности формы и нелинейности препятствуют для большинства действительно существующих конструкций осуществлению теоретической потери устойчивости.
Таким образом, исследование потери устойчивости при помощи собственных значений часто порождает неконсервативные результаты при неучете этих эффектов.
Несмотря на неконсервативность результатов, этот тип анализа весьма выгоден в смысле ресурсоемкости по сравнению с нелинейным анализом устойчивости.

О линейном анализе устойчивости
Для линейного расчета устойчивости основное уравнение, решаемое в задаче с целью определения множителя нагрузки λi и форм потери устойчивости ψi , имеет вид:
Допущения:
[K] и [S] – константы:
Принимается линейно-упругое поведение материала
Используется теория малых перемещений, и ВСЕ нелинейности исключаются
Важно помнить об этих допущениях при проведении линейного расчета устойчивости в ANSYS Mechanical.

Геометрия и свойства материалов
Любой тип геометрии, поддерживаемый ANSYS Mechanical может быть использован в анализе устойчивости:
Твердые тела
Поверхностные тела (с определением соответствующих толщин)
Линейные тела (с определением соответствующих сечений)
Для линейных тел доступны только результаты определения перемещений и вычисления форм потери устойчивости.
Несмотря на то, что точечные массы могут быть включены в модель, только инерционные нагрузки могут действовать на них, так что применяемость этой разновидности геометрии в анализе устойчивости может быть ограничена.
В качестве свойств материалов должны быть, как минимум, заданы модуль Юнга (Young’s Modulus) и коэффициент Пуассона (Poisson’s Ratio).

Нагрузки и опоры
Как минимум одна нагрузка, вызывающая потерю устойчивости, должна быть приложена к модели:
ВСЕ прочностные нагрузки будут умножены на множитель нагрузки (l) при определении критической нагрузки в точки бифуркации (см. ниже).
Граничные условия с опцией «только сжатие» (Compression-only) не рекомендуются.
Конструкция должна быть полностью закреплена для предотвращения перемещений в пространстве целиком.
F x l = Критическая нагрузка
При анализе на потерю устойчивости все приложенные нагрузки (F) масштабируются с коэффициентом (l) до достижения критической нагрузки, вызывающей потерю устойчивости.

Нагрузки и опоры
Следует особо отметить случаи наличия одновременно постоянных и пропорциональных нагрузок.
Можно итерационно изменять условия нагружения, подбирая переменные нагрузки, до тех пор пока множитель нагрузки не станет равным 1 или близким к 1.
Рассмотрим пример вертикального стержня с собственным весом WO под воздействием внешней силы A.
Решение может быть получено итерационно при подборе силы A до тех пор, пока λ не станет равным 1. Это будет гарантировать то, что собственный вес будет равен действительному, т.е. WO * λ = WO .

Обработка результатов
Интерпретация множителя нагрузки (λ):

Субмоделирование

О субмоделировании
Submodeling (субмоделирование) – конечно-элементная технология, позволяющая получить более точные результаты в отдельных областях модели. Эта технология позволяет рассмотреть области модели, предварительно сделав грубый расчет всей модели целиком, создать более подробную расчетную сетку и получить точные результаты в пределах рассматриваемой области. Технология доступна для прочностных и тепловых расчетов для твердотельной геометрии.

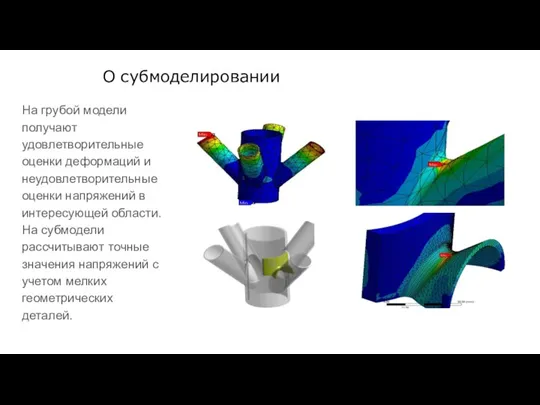
О субмоделировании
Процедура начинается с расчета на «грубой» сетке. Затем выбирается часть модели, представляющая интерес, и выполняется ее расчет на «хорошей» сетке.
Последняя модель носит название «субмодель». Она может содержать геометрические детали, которые не включены в исходную модель.

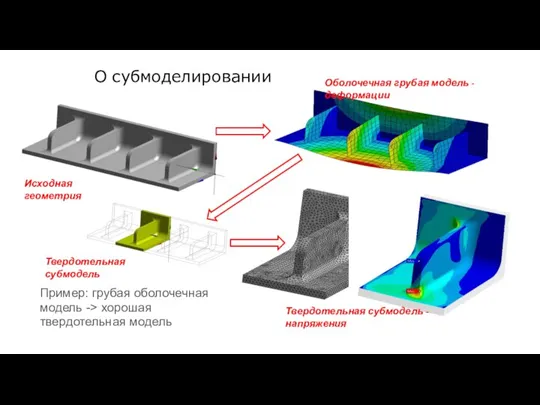
О субмоделировании
На грубой модели получают удовлетворительные оценки деформаций и неудовлетворительные оценки напряжений в интересующей области.
На субмодели рассчитывают точные значения напряжений с учетом мелких геометрических деталей.

О субмоделировании
Перемещения, посчитанные на грубой сетке на границе субмодели, передаются в саму субмодель.

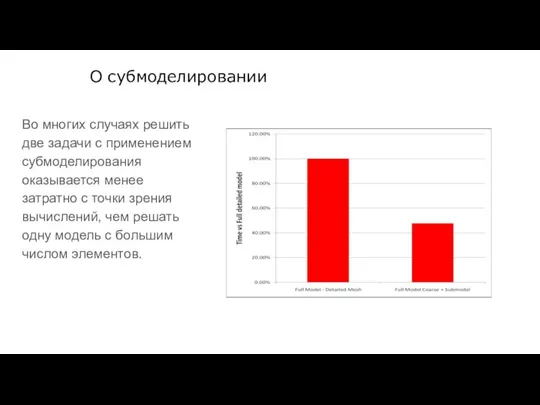
О субмоделировании
Во многих случаях решить две задачи с применением субмоделирования оказывается менее затратно с точки зрения вычислений, чем решать одну модель с большим числом элементов.

О субмоделировании
Исходная геометрия
Оболочечная грубая модель - деформации
Твердотельная субмодель - напряжения
Пример: грубая оболочечная модель -> хорошая твердотельная модель
Твердотельная субмодель

Порядок проведения расчетов

Типы решателей
Прямой
X=F*K-1
Итеративный
K*X1=F
K*X2=F
K*X3=F
…
KX=F

Временные и машинные ресурсы.
32 cores, RAM 256 GB

Параметрические исследования

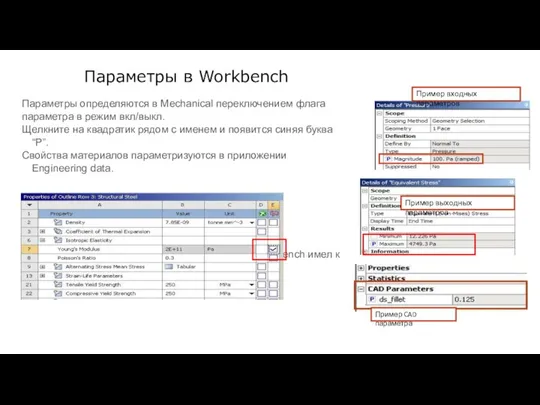
Параметры в Workbench
Параметры определяются в Mechanical переключением флага параметра в режим вкл/выкл.
Щелкните на квадратик рядом с именем и появится синяя буква “P”.
Свойства материалов параметризуются в приложении Engineering data.
CAD параметры надо также обозначать, чтобы Workbench имел к ним доступ (иначе они будут только для чтения).
Пример входных параметров
Пример CAD параметра

Параметры в Workbench
Workbench Mechanical использует приложение Parameter Workspace для управления параметрическими данными из расчетных и геометрических источников.
Здесь можно не только создать параметры и константы, но и управлять ими.
Двойной клик или щелчок ПКМ > Edit на объекте «Parameter Set» для входа в Parameter Workspace.

Параметры в Workbench
Информация о параметрах представлена в наборе таблиц:
Outline: перечисление всех входных, выходных и выводимых параметров.
Properties: приводит информацию для параметра, выделенного в таблице outline.
Таблица расчетных точек (Design Points): позволяет подготовить несколько конфигураций нескольких параметров для проведения расчетов
Outline
Таблица расчетных точек
Properties

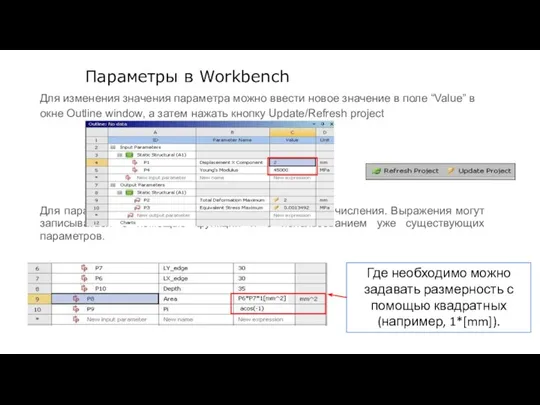
Параметры в Workbench
Для изменения значения параметра можно ввести новое значение в поле “Value” в окне Outline window, а затем нажать кнопку Update/Refresh project
Для параметров можно задавать выражения для их вычисления. Выражения могут записываться с помощью функций и с использованием уже существующих параметров.
Где необходимо можно задавать размерность с помощью квадратных (например, 1*[mm]).

Параметры в Workbench
Для ввода нескольких значений параметра используется таблица расчетных точек (Table of Design Points). Это позволяет прописать несколько сценариев изменения параметров в параметрических расчетах.
После заполнения таблицы расчетных точек нажмите на кнопку “Update All Design Points” для автоматического расчета всех точек по заданному сценарию. По умолчанию, каждый набор параметров переписывает существующий в Mechanical, протоколируя только значения выходных параметров. Если Вам нужно сохранить параметры конструкции в наборе, проверьте флажок “Retain” в нужной строчке таблицы.

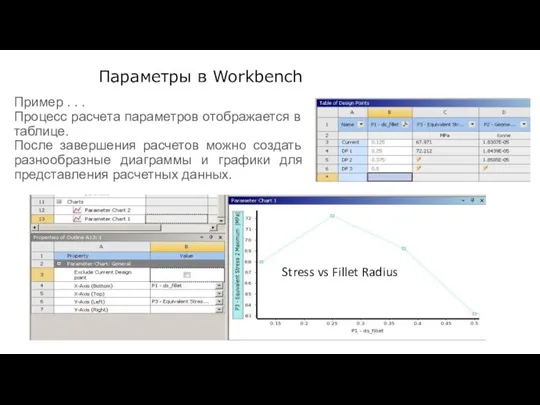
Параметры в Workbench
Пример . . .
Процесс расчета параметров отображается в таблице.
После завершения расчетов можно создать разнообразные диаграммы и графики для представления расчетных данных.
Stress vs Fillet Radius

Суперкомпьютеры, кластерные вычисления

Динамические расчеты

Определения и назначение
В динамическом расчете обычно исследуют следующие аспекты:
Свободные колебания
Собственные формы и частоты колебаний
Вынужденные колебания
Например, коленчатых валов и прочих вращающихся элементов машин и конструкции при гармоническом воздействии
Сейсмические/ударные нагрузки
Например, взрывы, землетрясения
Случайные колебания
Например, при взлете ракеты или колебания транспортных средств при движении
Переменные во времени нагрузки
Например, столкновения автомобилей, удар молота
Для каждого из этих аспектов есть отдельная расчетная система.

Рассмотрим следующие примеры:
Выхлопная система автомобиля может разрушиться, если ее собственные частоты совпадут с главными частотами двигателя. Как можно этого избежать?
Лопатка турбины при наличии напряжений (под центробежной нагрузкой) меняет свое динамическое поведение. Как можно это учесть?
Для определения динамических характеристик можно провести модальный расчет.
Типы динамических расчетов

При вращении роторов возникают установившиеся знакопеременные силы, действующие на подшипники и опоры. Эти силы вызывают перемещения и напряжения, зависящие от скорости вращения.
Вывод – нужно провести гармонический расчет для определения отклика конструкции при установившейся, гармонической нагрузке.
Типы динамических расчетов

Агрегаты космических кораблей и самолетов должны выдержать случайное нагружение в заданном диапазоне частот в течении заданного периода времени.
Решение – провести расчет при случайной вибрации для определения отклика агрегатов
Типы динамических расчетов

Небоскребы, сооружения ответственного назначения, мосты в сейсмоопасной зоне должны конструироваться так, чтобы выдерживать множественные коротковременные ударные нагрузки, характерные для сейсмики.
Для определения отклика конструкции на сейсмическое нагружение можно провести спектральный анализ.
Типы динамических расчетов

Типы динамических расчетов
Автомобильный бампер может устоять при невысокой скорости соударения, но разрушится при большой.
Теннисная ракетка должна быть сконструирована так, чтобы выдержать удар по мячу, будучи при этом достаточно гибкой.
Решение – провести переходной динамический расчет для определения отклика конструкции на изменяющиеся во времени нагрузки.

Выбор подходящего типа расчета зависит от типа входных данных и того, что нужно получить в результате.
Типы динамических расчетов

Общее уравнение движения
Принципы моделирования
Демпфирование
Основные понятия и термины

Общее уравнение движения
Общее линейное дифференциальное уравнение вынужденных колебаний в матричной форме имеет вид:
Обратите внимание на простое соотношение силового баланса:

Общее уравнение движения
Различные типы расчетов рассматривают частные случае этого уравнения.
Модальный
F(t) равно нулю; [C] обычно игнорируется.
Гармонический
F(t) и u(t) изменяются по гармоническому закону.
Спектральный
Входом является известный спектр величин на различных частотах в заданных направлениях.
При случайной вибрации
Входом является заданная спектральная плотность величин на различных частотах в заданных направлениях.
Нестационарный
Рассматривается полное уравнение в наиболее общем виде.

К геометрии и сетке в основном применяются те же требования, что и при статическом расчете.
Модель должна быть достаточно подробной, чтобы полностью отразить динамику конструкции.
В зонах, где интересуют напряжения, может понадобиться плотная сетка. Если Вам важны только перемещения либо частоты, может оказаться достаточной грубая сетка.
Принципы моделирования
Геометрия и сетка

Принципы моделирования Нелинейности
Нелинейности, такие как большие прогибы, нелинейный контакт, нелинейности материала и т.д., учитываются только в полном переходном расчете с включенной опцией учета больших прогибов (large deflection).
Все другие типы динамических расчетов линейны.
Начальное состояние всех нелинейных элементов расчета фиксируется в начальный момент и удерживается в процессе расчета, т.е. [K] = const.

Принципы моделирования
Свойства материала
Инерционные свойства [M]
Например, плотность, точечные массы
Требуется во всех динамических расчетах
Плотность массы задавайте в метрической системе
Плотность веса (если она нужна) задавайте в британской системе единиц
Свойства демпфирования [C]
Например, вязкое трение, демпфирование в материале (см. далее)
Требуется для гармонического расчета методом суперпозиции форм колебаний
Необязательно, но рекомендуется к определению во всех типах расчетов для корректности расчета
Упругие свойства (жесткость) [K]
Например, модуль Юнга, коэффициент Пуассона, модуль сдвига
Необходимы для всех расчетов деформируемых тел

Демпфирование – характеристика диссипации энергии в конструкции, приводящая к постепенному затуханию колебаний вплоть до полной их остановки.
Чаще всего энергия колебаний рассеивается в тепло или переходит в звуковые колебания
Количественно мера демпфирования определяется свойствами материала, скоростью колебаний и/или частотой.
Демпфирование
В ANSYS существует несколько видов потерь:
Вязкое трение (например, гидравлические амортизаторы, демпферы)
Трение в материале/гистерезисное демпфирование (внутреннее)
Сухое или кулоновское трение (например, при скольжении)
Численное демпфирование

Если мера демпфирования достаточно высока, то колебания конструкции или ее элементов прекращаются вплоть до апериодического движения.
Критическое затухание определяется как пороговое значение демпфирования, при котором колебательное движение переходит в апериодическое.
Коэффициентом демпфирования называется отношение демпфирования в системе к критическому затуханию
Демпфирование
k – жесткость, m – масса, ωn – собственная частота консервативной системы.

Собственная частота консервативной одномассовой системы (без трения)
Добавление к этой системе линейно-вязкого демпфирования, смещает собственную частоту:
Кулоновское трение не изменяет собственной частоты.
Демпфирование

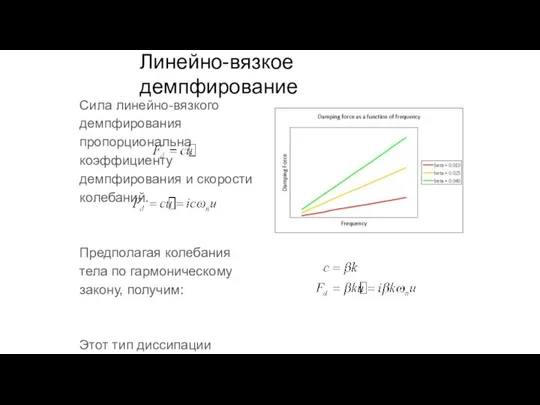
Сила линейно-вязкого демпфирования пропорциональна коэффициенту демпфирования и скорости колебаний.
Предполагая колебания тела по гармоническому закону, получим:
Этот тип диссипации характерен для систем с жидкостным демпфированием.
В расчетах конструкций для численного упрощения расчетов c часто заменяется на величину, пропорциональную жесткости с коэффициентом β.
Линейно-вязкое демпфирование

Потери присутствуют и в самих материалах по природе (энергия рассеивается за счет внутреннего трения), так что обычно оно учитывается при динамических расчетах.
Эксперименты доказывают, что гистерезисное демпфирование – частотно независимое.
Работа механизмов внутреннего трения достаточно сложна для понимания, так что для упрощения оно учитывается в расчетах множителем жесткости.
Трение в материале/гистерезисное демпфирование

Коэффициент демпфирования нельзя учесть в расчете типа transient, т.к. частотный отклик не рассчитывается.
Значение β может быть определено по известному значению ζ (коэффициента демпфирования) и частоты колебаний ω:
При вычислении β выбирайте самую мощную частоту с самым большим откликом.
Величину ζ в выражении
можно ввести в расчет как глобальную величину демпфирования (global damping value) или как демпфирование материала (material-dependent damping value).
Трение в материале/гистерезисное демпфирование

Кулоновское или сухое трение
Кулоновское трение появляется в системе при скольжении тела по сухой поверхности.
Сила сухого трения пропорциональна нормальной реакции.
μ – коэффициент сухого трения
m – масса тела
g – ускорение свободного падения
sgn(y) – функция знака:
При проведении линейного динамического расчета не учитывается. Учитывается при нелинейных transient расчетах.

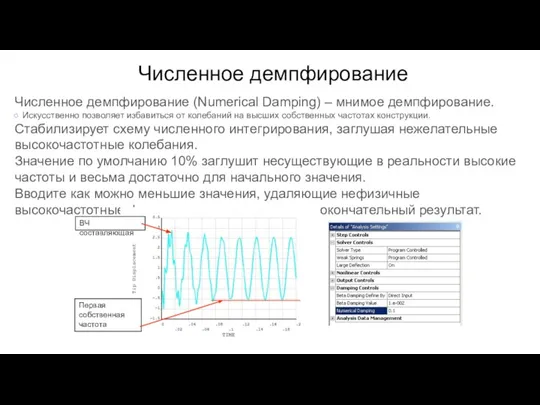
Численное демпфирование (Numerical Damping) – мнимое демпфирование.
Искусственно позволяет избавиться от колебаний на высших собственных частотах конструкции.
Стабилизирует схему численного интегрирования, заглушая нежелательные высокочастотные колебания.
Значение по умолчанию 10% заглушит несуществующие в реальности высокие частоты и весьма достаточно для начального значения.
Вводите как можно меньшие значения, удаляющие нефизичные высокочастотные формы, незначительно меняя окончательный результат.
ВЧ составляющая
Первая собственная частота
Численное демпфирование

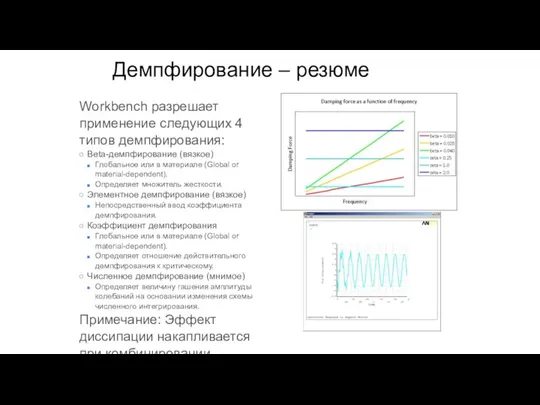
Workbench разрешает применение следующих 4 типов демпфирования:
Beta-демпфирование (вязкое)
Глобальное или в материале (Global or material-dependent).
Определяет множитель жесткости.
Элементное демпфирование (вязкое)
Непосредственный ввод коэффициента демпфирования.
Коэффициент демпфирования
Глобальное или в материале (Global or material-dependent).
Определяет отношение действительного демпфирования к критическому.
Численное демпфирование (мнимое)
Определяет величину гашения амплитуды колебаний на основании изменения схемы численного интегрирования.
Примечание: Эффект диссипации накапливается при комбинировании различных видов демпфирования.
Демпфирование – резюме

В различных случаях демпфирование может быть задано по разному:
ζ = Коэффициент линейно-вязкого трения или коэффициент демпфирования
η = Коэффициент потерь или Коэффициент конструкционного демпфирования
Q = Коэффициент добротности
Δ = Логарифмический декремент
D = Спектральное демпфирование
A = Коэффициент усиления
Преобразование одной величины в другую приведено в таблице (U = энергия деформации)
Демпфирование – резюме

Постпроцессинг

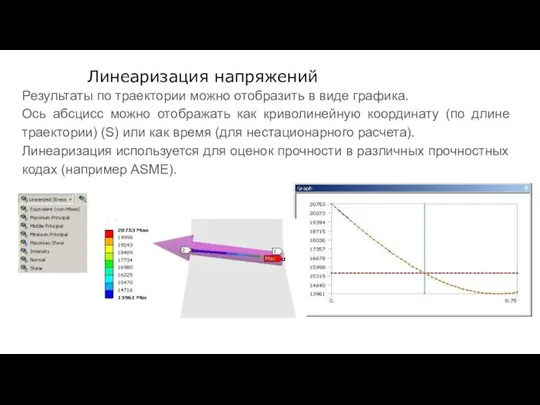
Линеаризация напряжений
Результаты по траектории можно отобразить в виде графика.
Ось абсцисс можно отображать как криволинейную координату (по длине траектории) (S) или как время (для нестационарного расчета).
Линеаризация используется для оценок прочности в различных прочностных кодах (например ASME).

Оценка погрешностей
Посредством инструмента оценки погрешности (например напряжения для статического расчета или тепловой поток для теплового расчета) можно определить области модели с высокой погрешностью расчета. Таким образом можно идентифицировать области требующие улучшения сетки.
Эпюра погрешностей используется для определения областей модели где потенциальная энергия на элементах сильно отличается.
Фактическое значение самой энергии не имеет большого значения.
Mesh Refinement

Сходимость
В большинстве случаев МКЭ-анализа если улучшить сетку то получатся более точные результаты. Требуется опыт чтобы оценить, насколько такого улучшения "достаточно". Mechanical имеет инструмент Convergence, который может помочь оценить качество сетки.
Получение оптимальной сетки требует:
Наличия критериев для определения, является ли сетка адекватной.
Сгущать сетку только там, где это необходимо.
Добавьте инструмент convergence к результату и установите значение в поле “allowable change”
Задайте максимальное число итераций

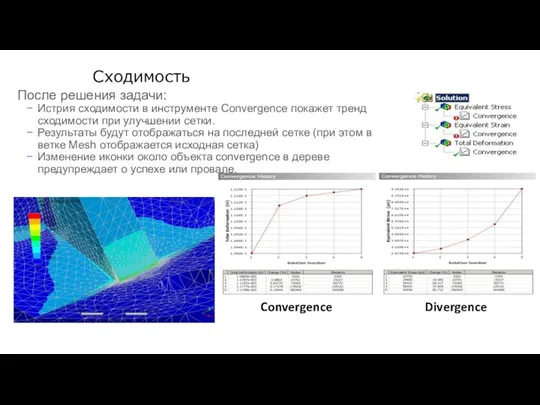
Сходимость
После решения задачи:
Истрия сходимости в инструменте Convergence покажет тренд сходимости при улучшении сетки.
Результаты будут отображаться на последней сетке (при этом в ветке Mesh отображается исходная сетка)
Изменение иконки около объекта convergence в дереве предупреждает о успехе или провале.
Convergence
Divergence

Сходимость
Инструмент Convergence не может быть использован если:
Модель содержит объект mesh connection.
В модели есть ссылки на другие ячейки анализа (как вверх так и вниз).
Нагрузки в модели получены посредством импорта.
Чтобы использовать Convergence, необходимо установить значение поля “Calculate Stress” на “Yes” в секции Output Controls деталей Analysis Settings.

Сингулярность напряжений
В статическом расчете есть несколько ситуаций которые приводят к сингулярности. Эти “искусственные” области повышенных напряжений могут привести к некорректным оценкам погрешностей и сходимости.
Если площадь 0

Сингулярность напряжений
Рассмотрим влияние сингулярности на оценку погрешности. Эта ситуация приведет к бесконечному сгущении сетки, причем безуспешно.
Чтобы решить эту проблему, мы должны либо удалить особенность (например, задать более реалистичные нагрузки и/или геометрию), или мы должны избегать оценок в проблемных областях.
.
Точечная нагрузка
Высокий градиент энергии

Сингулярность напряжений
Если область сингулярности не представляет интереса, то добавляйте инструмент convergence в области, где будет проводится оценка прочности и др.
Пример:
Возможное место сингулярности
Интересующая область

Сингулярность напряжений
Инструмент Convergence добавленный на полную модель
Особенности геометрии вызывают расхождение.
Инструмент Convergence добавлен только на интересующую область.
Обеспечен контроль над качеством сетки и адаптивным решением.
В интересующей области получены результаты с высокой точностью.

Нелинейные задачи

В 1600-х годах Роберт Гук установил простое линейное математическое соотношение между нагрузкой (F) и перемещением (u), известное как закон Гука: F = Ku,
где постоянная матрица K представляет собой жесткость.
Линейная конструкция подчиняется именно этому закону. Простейший пример – линейная пружина:
Линейные конструкции хорошо обсчитываются методом конечных элементов (МКЭ), который основан на законах линейной матричной алгебры.
Что такое нелинейное поведение?

Значительная часть конструкций НЕ имеют линейной взаимосвязи нагрузки и вызванных ею перемещений.
Отсюда график функции внешней нагрузки F от перемещения u для таких конструкций НЕ является прямой линией. Такие конструкции называют нелинейными.
Жесткость такой конструкции K не является постоянной; она является функцией приложенной нагрузки; KT это так называемая касательная жесткость - tangent stiffness).
Наиболее яркий пример – растяжение образца из нехрупкого металла:
F
u
KT
Что такое нелинейное поведение?

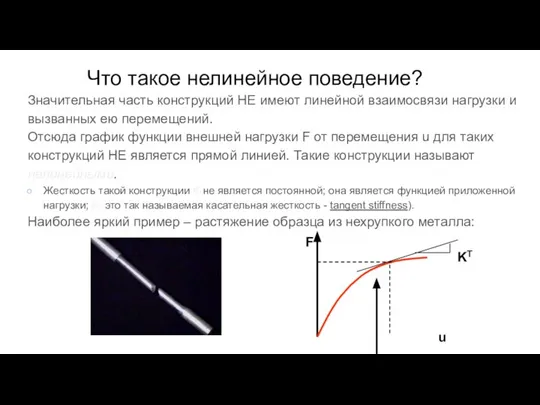
Что такое нелинейное поведение?
Поведение конструкции считается нелинейным, если нагрузка вызывает значительное изменение жесткости. Основные причины:
Возникновение деформаций за пределами упругости (пластичность)
Большие прогибы (подобно рыболовной удочке)
Изменяющийся статус элементов (например, контакт между телами, рождение/смерть элементов)
Что такое нелинейное поведение?

Нелинейное поведение конструкции проявляется в нескольких случаях, которые можно сгруппировать в 3 главные категории:
Наличие геометрических нелинейностей: больших деформаций (Large Strains), больших прогибов (Large Deflections), упрочнения материала (Stress Stiffening) и размягчения материала (Spin Softening);
Наличие нелинейностей материала (пластичности, гиперупругости, ползучести);
Наличие нелинейностей изменяющегося состояния (контакт).
Типы нелинейностей

И естественно, все три типа нелинейностей часто встречаются в пределах одной задачи.
Mechanical может легко комбинировать все типы нелинейных эффектов.
Расчет резинового уплотнения
Яркий пример одновременного учета геометрических нелинейностей (больших прогибов и деформаций), нелинейных свойств материала (резины) и нелинейностей изменяющегося состояния (контакта).
Типы нелинейностей

Как Mechanical решает задачу в условиях изменяющейся жесткости?
В нелинейных задачах отклик конструкции на внешнюю нагрузку не может быть определен системой линейных уравнений.
Тем не менее, нелинейная конструкция может быть подвергнута анализу с помощью серии итерационных линейных приближений с последовательной корректировкой жесткости и других величин.
ANSYS использует алгоритм итерационного процесса, называемый методом Ньютона-Рафсона (Newton-Raphson method). Каждая итерация называется равновесной (equilibrium iteration).
Полная процедура итерационного расчета методом Ньютона-Рафсона для одного приращения нагрузки. (Показаны 4 итерации)
Решение нелинейных задач

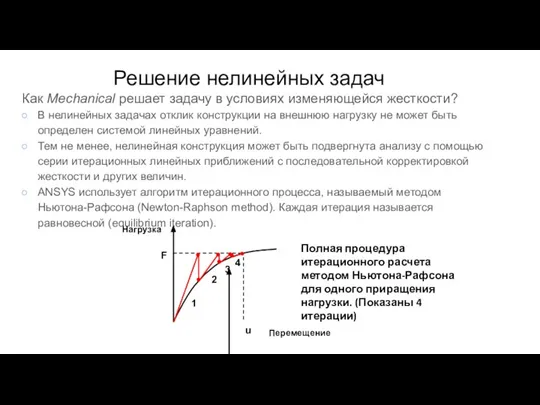
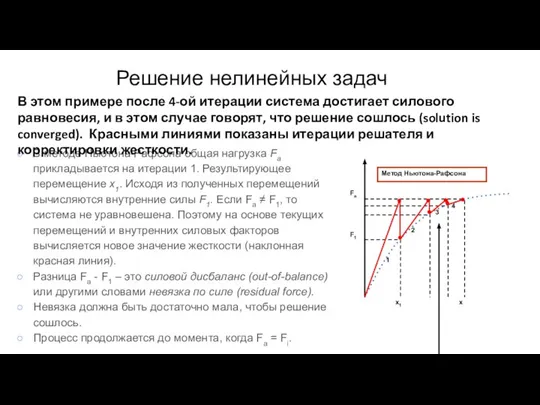
В методе Ньютона-Рафсона общая нагрузка Fa прикладывается на итерации 1. Результирующее перемещение x1. Исходя из полученных перемещений вычисляются внутренние силы F1. Если Fa ≠ F1, то система не уравновешена. Поэтому на основе текущих перемещений и внутренних силовых факторов вычисляется новое значение жесткости (наклонная красная линия).
Разница Fa - F1 – это силовой дисбаланс (out-of-balance) или другими словами невязка по силе (residual force).
Невязка должна быть достаточно мала, чтобы решение сошлось.
Процесс продолжается до момента, когда Fa = Fi.
В этом примере после 4-ой итерации система достигает силового равновесия, и в этом случае говорят, что решение сошлось (solution is converged). Красными линиями показаны итерации решателя и корректировки жесткости.
Решение нелинейных задач

Разница между внешней и внутренней нагрузкой {Fa} - {Fnr} называется невязкой (residual). Это мера силового дисбаланса конструкции.
Цель процесса – приращать перемещения до момента, пока невязка не станет достаточно малой или другими словами до наступления сходимости решения.
При достижении сходимости, конструкция уравновешена с заданной точностью.
{Fa}
{Fnr}
Fa
Fnr
u
{
Решение нелинейных задач

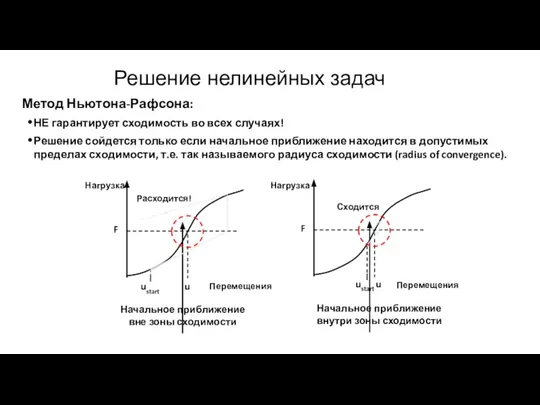
Метод Ньютона-Рафсона:
НЕ гарантирует сходимость во всех случаях!
Решение сойдется только если начальное приближение находится в допустимых пределах сходимости, т.е. так называемого радиуса сходимости (radius of convergence).
Решение нелинейных задач
Начальное приближение вне зоны сходимости
Начальное приближение внутри зоны сходимости

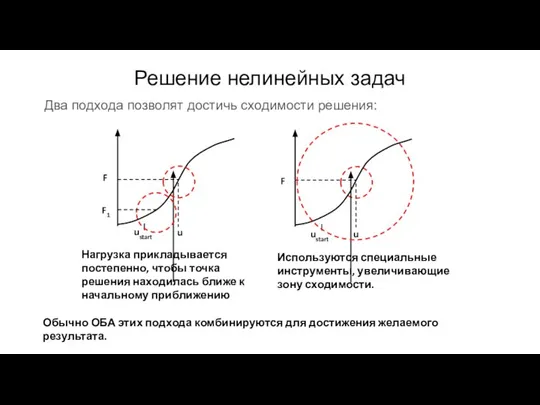
Два подхода позволят достичь сходимости решения:
Решение нелинейных задач
F
u
ustart
F1
Используются специальные инструменты, увеличивающие зону сходимости.
Обычно ОБА этих подхода комбинируются для достижения желаемого результата.

Общее замечание: внезапные изменения состояния конструкции всегда вызывают трудности при достижении сходимости.
Fa
xa
Fb
xb
Fa1
Fb2
Fb1
Решение нелинейных задач
Настройка нагружения в ANSYS
Шаги нагружения (Load steps) позволяют различить и разделить изменения в общей картине нагружения. На рисунке Fa и Fb это нагрузка на шагах.
Подшаги (Substeps) – это части общей нагрузки, приложенные постепенно.
Из-за необходимости определения нелинейного отклика и сложности этой процедуры часто необходимо прикладывать нагрузку постепенно.
Например, Fa1 составляет примерно 50% общей нагрузки Fa. После достижения сходимости для нагрузки Fa1 прикладывается полная нагрузка Fa. Fa имеет 2 подшага нагружения, а, например, Fb – 3 подшага.
Равновесные итерации – это откорректированные решения, полученные на каждом сошедшемся подшаге нагружения
На рисунке они показаны тонкими пунктирными линиями.

Обычно в нелинейных задачах именно достижение сходимости самый трудоемкий аспект решения.
Начальное приближение решения должно быть внутри радиуса сходимости.
Заранее радиус сходимости неизвестен.
Если решение сошлось, значит начальное приближение было выбрано правильно.
Если не сошлось – начальное приближение было вне радиуса сходимости.
Иногда потребуется действовать методом проб и ошибок.
Опыт решения задач поможет Вам уменьшить количество действий с непредсказуемым исходом.
Проблемы сходимости могут быть решены уменьшением шага, увеличением количества итераций при приложении нагрузки и др.
Решение нелинейных задач

Понятие пластичности

Вспомним законы упругости:
Перед тем, как заняться пластичностью, полезно вспомнить основные положения теории линейной упругости.
При абсолютно упругом поведении если возникающие в материале напряжения не превышают предел текучести, то материал полностью восстановит свою исходную форму при снятии нагрузки.
С точки зрения металлов это поведение вызвано растяжением без разрыва межмолекулярных связей.
Растяжение межмолекулярных связей полностью восстанавливается
Упругие деформации крайне малы.
Линейно упругое поведение материалов в наиболее общем виде описывается законом Гука, связывающим компоненты напряжений и деформаций:
Упругость и пластичность

Что такое пластичность?
Когда эластичный материал испытывает напряжения выше предела упругости, он течет, получая большие постоянные перемещения.
Пластичность описывает поведение материала за пределом текучести.
Учет пластичности важен при расчете операций формовки металлов.
Пластичность также важна как механизм поглощения энергии в реальных конструкциях и механизмах.
О материалах, разрушающихся при небольших пластических деформациях, говорят, что они хрупкие.
Эластичное поведение материала безопаснее хрупкого отклика.
Пластичность – наиболее часто используемая нелинейность материала в ANSYS.
Упругость и пластичность

Пластические деформации получаются из-за взаимного проскальзывания молекулярных пластов (дислокаций) из-за наличия сдвиговых напряжений. Это движение дислокаций описывает процесс смещения, перегруппировки атомов кристаллической решетки, при котором образуются новые межатомные связи с новыми «соседями».
В результате наблюдаются невосстанавливаемые пластические деформации, остающиеся в материале после снятия нагрузки.
Движение дислокаций при этом, в отличие от упругости, обычно не вызывает объемных деформаций (условие несжимаемости)
Упругость и пластичность

В общем случае в теле образуется многоосное напряженное состояние.
В большинстве же случаев параметры пластического поведения определяется на основе одноосных испытаний образцов.
При этом образуется одноосное напряженное состояние, из которого определяются следующие свойства материала:
Предел пропорциональности
Предел текучести
Пластическое упрочнение
Упругость и пластичность

Пределы пропорциональности и текучести
Большинство пластичных материалов ведут себя линейно при напряжениях меньше предела пропорциональности
Ниже предела пропорциональности напряжение линейно зависит от деформации.
При напряжениях ниже предела текучести материал ведет себя упруго.
Ниже предела текучести любая деформация исчезает при снятии нагрузки (нет остаточных деформаций).
Упругость и пластичность

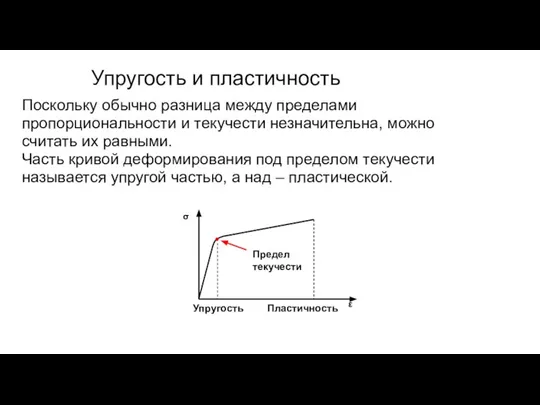
Поскольку обычно разница между пределами пропорциональности и текучести незначительна, можно считать их равными.
Часть кривой деформирования под пределом текучести называется упругой частью, а над – пластической.
Упругость и пластичность

Упрочнение
После преодоления предела пластичности поведение обычно характеризуется идеальной пластичностью или пластическим упрочнением.
Пластическое упрочнение – это поведение материала, при котором предел текучести возрастает вместе с увеличением напряжения.
Одноосное напряженное состояние
Упругость и пластичность

Пластичность, не зависящая от скорости
Если отклик материала не зависит от скорости нагружения или деформирования, имеем дело с пластичностью, не зависящей от скорости.
Пределы текучести обычно выше при более высоких скоростях деформации.
Большинство металлов испытывают именно эту разновидность пластичности при низких температурах (<1/4 или 1/3 температуры плавления) и при небольших скоростях деформации
Упругость и пластичность

Критерий текучести (Yield criterion)
Используется для соотнесения многоосного напряженного состояния с одноосным.
Для случая одноосного растяжения образца состояние текучести может быть сразу определено сравнением осевых напряжений с пределом текучести материала. Однако для случая многоосного напряженного состояния необходимо определить критерий текучести.
Критерий текучести – это скалярная величина, оценивающая напряженное состояние, которую можно непосредственно сравнить с пределом текучести для одноосного напряженного состояния.
Критерий текучести

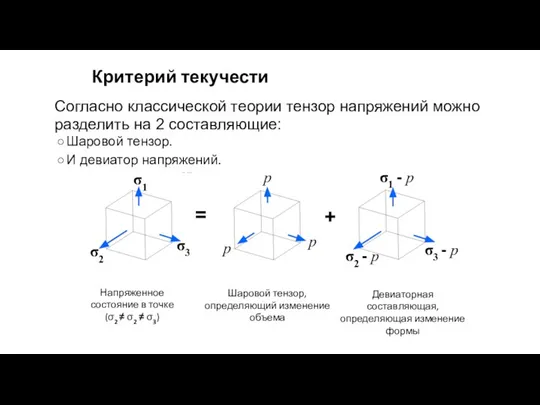
Согласно классической теории тензор напряжений можно разделить на 2 составляющие:
Шаровой тензор.
И девиатор напряжений.
Критерий текучести
Напряженное состояние в точке
(σ2 ≠ σ2 ≠ σ3)
Шаровой тензор, определяющий изменение объема
Девиаторная составляющая, определяющая изменение формы
p
σ2
σ3
σ1
p
σ2 - p
p
σ1 - p
σ3 - p
=
+

Наиболее общий критерий текучести – это критерий фон Мизеса (von Mises).
Течение начинается тогда, когда внутренняя энергия деформации (эквивалентные напряжения) превышают заданную величину.
Вводятся эквивалентные напряжения по фон Мизесу:
Здесь σ1, σ2 и σ3 – главные напряжения.
Течение начинается, когда эквивалентные напряжения превышают предел текучести материала
Критерий текучести

Критерий текучести фон Мизеса можно изобразить в пространстве осей главных напряжений:
Он представляет собой цилиндрическую поверхность, ориентированную относительно прямой σ1=σ2=σ3.
Она называется поверхностью текучести.
Если напряженное состояние определяется точкой внутри цилиндра, поведение материала – упругое, если на поверхности – пластическое.
Критерий текучести

Изменение пластических деформаций происходит согласно закону течения:
где dλ – множитель приращения деформации,
Q – пластический потенциал
Закон течения определяет то, как отдельные компоненты пластической деформации (εxpl, εypl и т.д.) изменяются в процессе течения.
Законы течения

Законы течения, в которых пластический потенциал равен критерию текучести, обычно подразумевают, что пластические деформации распространяются в направлении перпендикулярном к поверхности текучести.
Такие законы течения называются ассоциативными.
Все модели пластичности, реализованные в Workbench относятся к ассоциативным.
Законы течения, в которых пластический потенциал отличается от критерия текучести называются неассоциативными.
Законы течения

Закон упрочнения (Hardening rule)
На границе поверхности текучести происходит течение материала.
Напряженное состояние за пределами поверхности текучести невозможно.
Вместо этого при росте пластических деформаций происходит изменение поверхности текучести.
Как это происходит описывается законом упрочнения.
Закон упрочнения определяет как материал будет течь дальше, если нагружение продолжится или изменится направление нагрузки.
Законы упрочнения

Есть 2 главных закона упрочения, используемых ANSYS для описания характера поведения поверхности течения:
Кинематическое упрочнение (Kinematic hardening).
Поверхность течения сохраняет свой размер и перемещается в направлении течения.
Изотропное упрочнение (Isotropic hardening).
Поверхность течения равномерно расширяется при течении по всем направлениям.
Большинство металлов испытывают именно кинематическое упрочнение при циклическом нагружении в рамках малых деформаций.
Законы упрочнения

Кинематическое упрочнение
Соотношение между напряжениями и деформациями для линейного кинематического упрочнения представлено на рисунке:
Предел текучести при последующем сжатии образца меньше по модулю, чем аналогичная величина при начальном растяжении, но всегда между состояниями поддерживается разница 2σy. (Это явление называется эффектом Баушингера)
ε
σ2
σ1
2σy
σy
σ'
Initial Yield Surface
Subsequent Yield Surface
α
Законы упрочнения

Изначально изотропный материал перестает быть изотропным, как только начинает течь и испытывать кинематическое упрочнение.
Для очень большого класса задач модель кинематического упрочнения может стать непригодной именно из-за эффекта Баушингера.
Кинематическое упрочнение обычно используется при небольших деформациях в расчетах с циклической нагрузкой.
ε
σy
2σy
σ’
Законы упрочнения

Изотропное упрочнение
Соотношение между напряжениями и деформациями для изотропного упрочнения представлено на рисунке:
Равномерно расширяется в процессе течения. Термин «изотропный» относится к равномерному расширению поверхности течения и отличается от понятия изотропный критерий текучести.
ε
σ3
σ2
σ1
σ
2σ'
σy
σ'
Initial Yield Surface
Subsequent Yield Surface
Законы упрочнения

Обратите внимание, что предел текучести при последующем сжатии равен максимальному напряжению, полученному на фазе растяжения.
Изотропное упрочнение часто используется в расчетах с большими деформациями или пропорциональном (нециклическом) нагружении.
Законы упрочнения

Формы кривых (Curve shapes)
Модели пластичности в Workbench поддерживают два различных типа кривых:
Билинейная
(Bilinear)
Мультилинейная
(Multilinear)
Ввод данных о материале

Инженерные и истинные напряжения и деформации
Расчет задач пластичности при больших деформациях требует задания истинных напряжений (true stress) и логарифмических деформаций (log strain), тогда как для расчетов с малыми деформациям можно вводить инженерные значения значения.
Если данные эксперимента содержат только инженерные значения, то перед введением в ANSYS для задач с большими деформациями их необходимо конвертировать в истинные напряжения и логарифмические деформации.
True
Stress
Strain
Engineering
Ввод данных о материале