Содержание
- 2. ПОЛЯРИЗАЦИЯ СВЕТА
- 3. СВЕТОВОЙ ВЕКТОР. ЕСТЕСТВЕННЫЙ И ПОЛЯРИЗОВАННЫЙ СВЕТ
- 4. Согласно электромагнитной теории света Максвелла : СВЕТ – представляет собой электромагнитные волны распространяющиеся в среде с
- 5. Векторы , и образуют правовинтовую систему, век-торы и колеблются в одинаковых фазах, причем , мгновенные соотношения
- 6. ПОЛЯРИЗАЦИЯ Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы излучают свето-вые волны независимо друг от
- 7. ЕСТЕСТВЕННЫЙ СВЕТ – колебания све-тового вектора равновероятны по всем направлениям ЧАСТИЧНО ПОЛЯРИЗОВАННЫЙ СВЕТ – появляется (в
- 8. Плоскость , проходящая через направление колебаний светового вектора плоскополяризованной волны и на-правление распространения этой волны, называется
- 9. СТЕПЕНЬ ПОЛЯРИЗАЦИИ СТЕПЕНЬЮ ПОЛЯРИЗАЦИИ называется величина: Где: и – соответственно максимальная и мини-мальная интенсивности частично поляризованного
- 10. ПОЛЯРИЗАТОРЫ И АНАЛИЗАТОРЫ. ЗАКОН МАЛЮСА
- 11. Естественный свет можно преобразовать в плоскополяри-зованный с помощью ПОЛЯРИЗАТОРОВ, пропускающих колебания только определенного направления (напри-мер пропускающие
- 12. АНАЛИЗАТОРЫ Для определения характера и степени поляризации ис-пользуют АНАЛИЗАТОРЫ, в их роли могут выстутать те же
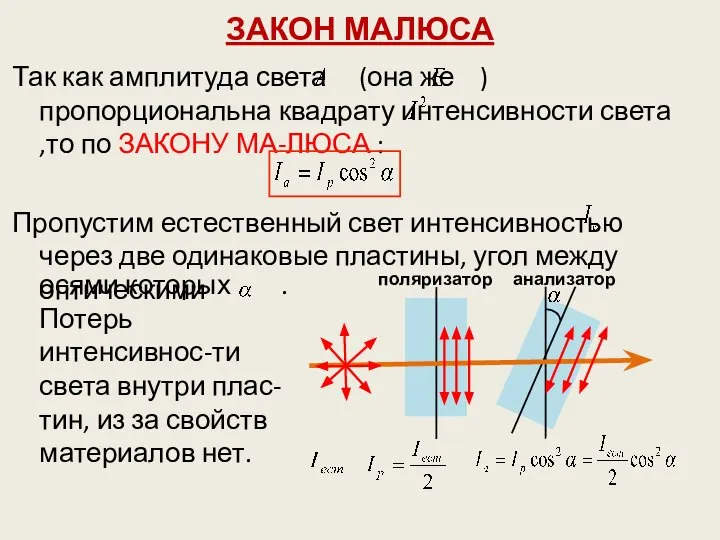
- 13. ЗАКОН МАЛЮСА Так как амплитуда света (она же ) пропорциональна квадрату интенсивности света ,то по ЗАКОНУ
- 14. При прохождении света через первую пласти-ну, служащую поляри-затором, естественный свет поляризуется, и совершает колебания в плоскости,
- 15. Если на пластину служащую анализатором падает естес-твенный свет, то она выступает в качестве поляриза-тора. Если у
- 16. ПОЛЯРИЗАЦИЯ СВЕТА ПРИ ОТРАЖЕНИИ И ПРЕЛОМЛЕНИИ СВЕТА НА ГРАНИЦЕ ДВУХ ДИЭЛЕКТРИКОВ
- 17. Если естественный свет падает на границу раздела двух диэлектриков, то часть его отражается, а часть прелом-ляется
- 18. Шотландский физик Д. Брюстер (1781-1868) вывел закон, согласно которому: При угле падения (угле Брюстера), оп-ределяемого соотношением:
- 19. Если свет падает на границу раздела двух сред под углом Брюстера, падающий, отраженный и преломленный лучи
- 20. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
- 21. Большинство кристаллов оптичес-ки анизотропно (не изотропно), иобладают свойством двойного лучепреломления, то есть раз- дваивания каждого падающего
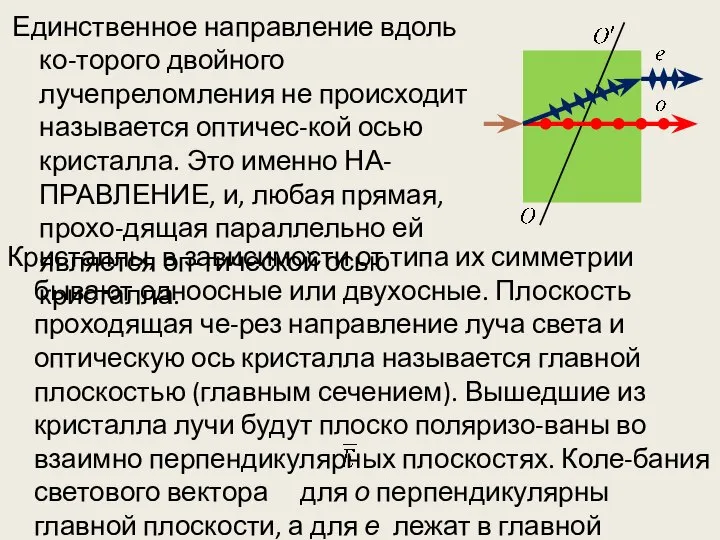
- 22. Единственное направление вдоль ко-торого двойного лучепреломления не происходит называется оптичес-кой осью кристалла. Это именно НА-ПРАВЛЕНИЕ, и,
- 23. СКОРОСТЬ РАСПРОСТРАНЕНИЯ СВЕТА В СРЕДЕ Неодинаковое преломление о и е, указывает на различ-ные для этих лучей
- 24. луча. Из этого следует, что о подчиняется закону пре-ломления, а для е в кристалле этот закон
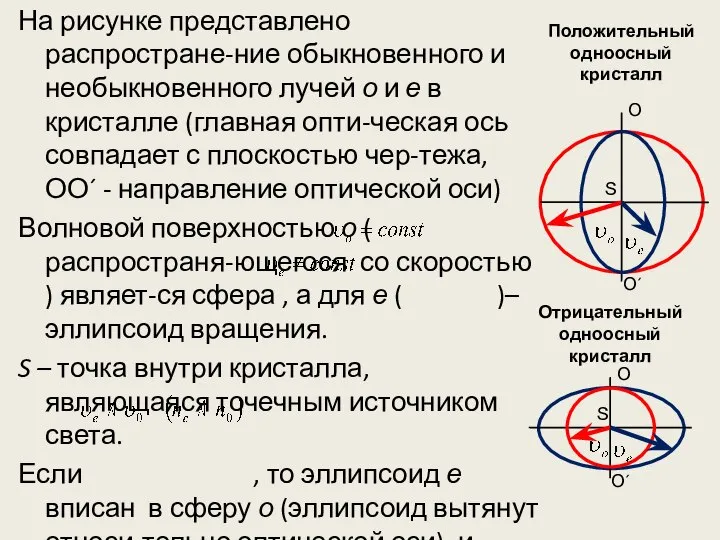
- 25. На рисунке представлено распростране-ние обыкновенного и необыкновенного лучей о и е в кристалле (главная опти-ческая ось
- 26. Наоборот, если , то эллипсоид описан вок-руг сферы (эллипсоид скоростей растянут в направле-нии, перпендикулярном оптической оси)
- 27. В основе работы поляризационных приспособлений, служащих для получения поляризованного света ле-жит явление двойного лучепреломления. Наиболее часто
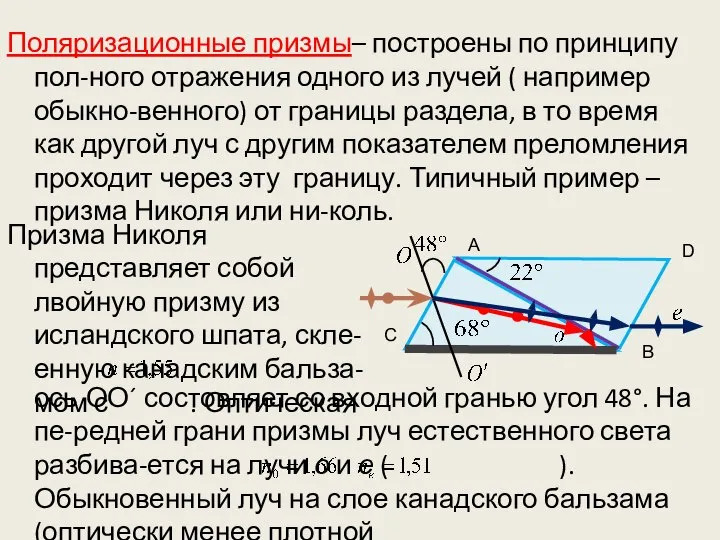
- 28. Поляризационные призмы– построены по принципу пол-ного отражения одного из лучей ( например обыкно-венного) от границы раздела,
- 29. среде) испытывает полное отражение, а затем погло-щается полностью зачернённой поверхностью CВ. Необыкновенный луч – выходит из
- 30. Двоякопреломляющие призмы обладают свойством ди-хроизма, то есть различного поглощения света, в зави-симости от ориентации электрического вектора
- 31. Поляроиды – тонкие пленки, обладающие ярко выраже-нным дихроизмом и преобразующие естественный свет в линейно поляризованный. Типичный
- 32. ИССКУСТВЕННАЯ ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
- 33. Двойное лучепреломление имеет место в естественных анизотропных средах. Однако, ещё в середине XIX в. Было обнаружено
- 34. Оптически изотропные вещества становятся оптически анизотропными под влиянием: Одностороннего сжатия или растяжения (фотоупру-гость)(для кристаллов кубической системы,
- 35. Мерой возникающей искуственной оптической деформа-ции служит разность показателей преломления обык-новенного и необыкновенного лучей в направлении перпендикулярном
- 36. ЭФФЕКТ КЕРРА Жидкий или твердый изотропный диэлектрик, помещен-ный в достаточно сильное однородное электрическое поле становится оптически
- 37. между электродами меняется анизотропия вещества, а значит и интенсивность света прошедшего через анализатор. На пути между
- 38. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ
- 39. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
- 40. ХАРАКТЕРИСТИКИ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 41. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ Нагретые до достаточно высоких температур тела светят-ся. Свечение обусловлено ТЕМПЕРАТУРНЫМ ТЕПЛО-ВЫМ ИЗЛУЧЕНИЕМ. Данное излучение
- 42. Если равновесие между телом и излучением по какой то причине нарушено , и тело излучает больше
- 43. ИЗЛУЧАТЕЛЬНОСТЬ ТЕЛА Количественной характеристикой теплового излучения служит СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГЕТИЧЕСКОЙ СВЕТИМОСТИ (ИЗЛУЧАТЕЛЬНОСТЬ) ТЕЛА. ИЗЛУЧАТЕЛЬНОСТЬ ТЕЛА –
- 44. Записанную формулу можно представить в виде функции длины волны: Так как , то Знак минус показывает
- 45. СПЕКТРАЛЬНАЯ ПОГЛОЩАТЕЛЬНАЯ СПОСОБНОСТЬ Способность тел поглощать падающее на них излучение характеризуется: СПЕКТРАЛЬНОЙ ПОГЛОЩАЮЩЕЙ СПОСОБНОСТЬЮ : Спектральная
- 46. частотами. Поэтому эти величины относят к опреде-ленным температурам и частотам (точнее к мак-симально узкому интервалу частот
- 47. АБСОЛЮТНО ЧЕРНОЕ ТЕЛО Тело, способное поглощать полностью, при любой темпе-ратуре всё падающее на него излучение называется:
- 48. СЕРОЕ ТЕЛО СЕРОЕ ТЕЛО – тело, поглощательная способность кото-рого меньше единицы, но одинаково для всех частот
- 49. ЗАКОН КИРХГОФА
- 50. Опираясь на второе начало термодинамики, и анализи-зруя условия равновесного излучения Кирхгоф устано-вил количественную связь между спектральной
- 51. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГЕТИЧЕСКОЙ СВЕТИМОСТИ ЧЕРНОГО ТЕЛА – УНИВЕРСАЛЬНАЯ ФУНКЦИЯ КИРХГОФА или спект-ральная плотность энергетической светимости черно-го
- 52. Из закона Кирхгофа следует что: любого тела, в любой области спектра, всегда меньше (при тех же
- 53. ЗАКОН СТЕФАНА-БОЛЬЦМАНА. ЗАКОН СМЕЩЕНИЯ ВИНА
- 54. ЗАКОН СТЕФАНА-БОЛЬЦМАНА Спектральная плотность энергетической светимости чер-ного тела является универсальной функцией, и на-хождение её явной зависимости
- 55. – постоянная Стефана-Больцмана Для серого тела закон Стефана-Больцмана имеет вид: – энергетическая светимость серого тела –
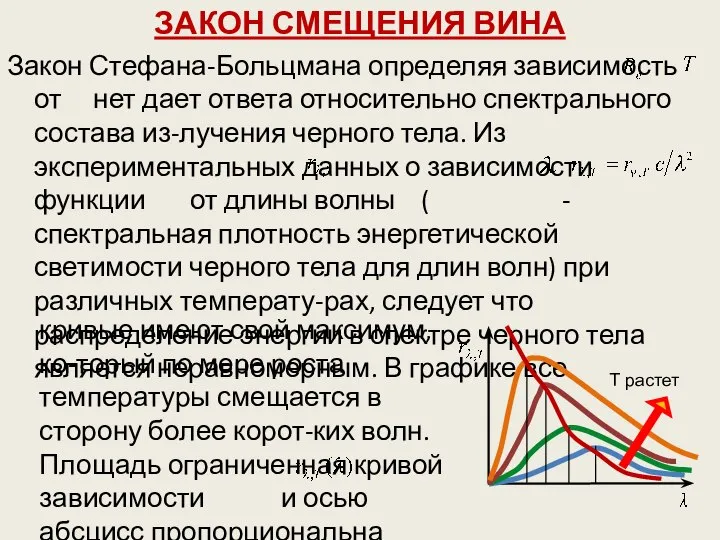
- 56. ЗАКОН СМЕЩЕНИЯ ВИНА кривые имеют свой максимум, ко-торый по мере роста температуры смещается в сторону более
- 57. тической светимости черного тела, и , по закону Стефана-Больцмана четвертой степени температуры. В.Вин установил зависимость длины
- 58. Закон смещения Вина показывает смещение положения максимума функции по мере возрастания темпера-туры в области коротких длин
- 59. ФОРМУЛА РЭЛЕЯ-ДЖИНСА. ФОРМУЛА ПЛАНКА. КВАНТЫ
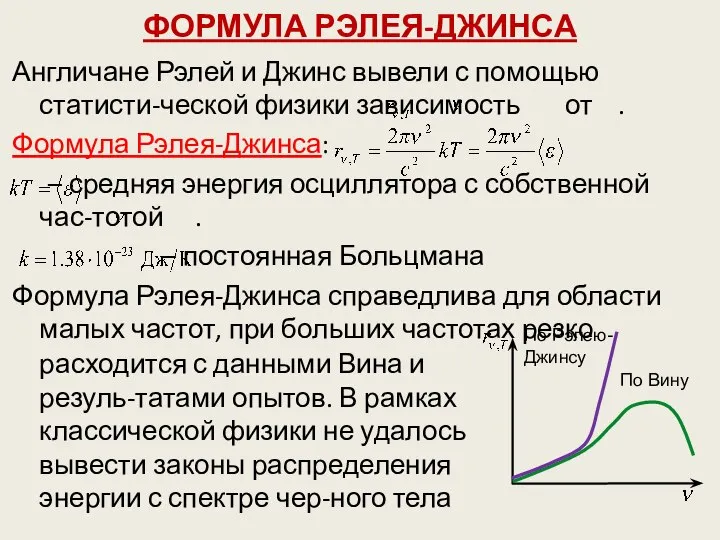
- 60. ФОРМУЛА РЭЛЕЯ-ДЖИНСА расходится с данными Вина и резуль-татами опытов. В рамках классической физики не удалось вывести
- 61. КВАНТОВАЯ ГИПОТЕЗА. ФОРМУЛА ПЛАНКА Правильное, соответствующее с опытными данными, выражение для спектральной плотности энергетичес-кой светимости было
- 62. Так ка излучение испускается порциями, то энергия ос-циллятора дискретна и кратна целому числу элемен-тарных значений энергии
- 63. Планк вывел формулу для универсальной функции Кирхго-фа: Данная формула согласуется с экспериментальными дан-ными по распределению энергий
- 64. ОПТИЧЕСКАЯ ПИРОМЕТРИЯ. ТЕПЛОВЫЕ ИСТОЧНИКИ СВЕТА
- 65. ОПТИЧЕСКАЯ ПИРОМЕТРИЯ Законы теплового излучения используются для измере-ния температуры раскаленных и недоступных для кон-тактного измерения температуры
- 66. РАДИАЦИОННАЯ ТЕМПЕРАТУРА РАДИАЦИОННАЯ ТЕМПЕРАТУРА – такая температура чер-ного тела, при котором его энергетическая светимость равна энергетической
- 67. ЦВЕТОВАЯ ТЕМПЕРАТУРА Для серых тел спектральная плотность энергетической светимости где . Значит распределе-ние энергии в спектре
- 68. ЯРКОСТНАЯ ТЕМПЕРАТУРА ЯРКОСТНАЯ ТЕМПЕРАТУРА – температура черного тела, при которой для определенной длины волны, его спек-тральная
- 69. В качестве яркостного пирометра обычно используется пирометр с исчезающей нитью накала. Нить накала подбирается так, что
- 71. Скачать презентацию






























































 Электромагниты. 8 класс
Электромагниты. 8 класс Презентация на тему Сила трения
Презентация на тему Сила трения  Введение в предмет Микросхемотехника
Введение в предмет Микросхемотехника Резисторы и Реостаты. Занятие 7
Резисторы и Реостаты. Занятие 7 Резонансные методы передачи электрической энергии
Резонансные методы передачи электрической энергии Закон Максвелла. Электромагнитное поле
Закон Максвелла. Электромагнитное поле Электризация тел
Электризация тел Как устроен строительный экскаватор и что такое гидравлический цилиндр?
Как устроен строительный экскаватор и что такое гидравлический цилиндр? Магнетизм. Структурно-логическая схема. Условные обозначения
Магнетизм. Структурно-логическая схема. Условные обозначения Работа по физике. Правду ли говорят
Работа по физике. Правду ли говорят Презентация на тему Влияние магнитных полей на живые организмы
Презентация на тему Влияние магнитных полей на живые организмы  Рулевое устройство
Рулевое устройство Фотометрия и светотехника. ВИК - простая форма обучения
Фотометрия и светотехника. ВИК - простая форма обучения Скин-фактор. Различные режимы притока. Уравнение притока
Скин-фактор. Различные режимы притока. Уравнение притока Дозиметрия. Период полураспада. Закон радиоактивного распада
Дозиметрия. Период полураспада. Закон радиоактивного распада Покоривший волны
Покоривший волны Расчет характеристик световой волны. Практическая работа №21
Расчет характеристик световой волны. Практическая работа №21 Поколения ядерных реакторов. Лекция 6
Поколения ядерных реакторов. Лекция 6 Мир вокруг нас
Мир вокруг нас Инструменты и приборы
Инструменты и приборы Механическая работа. Единицы работы
Механическая работа. Единицы работы Спектроскопические методы анализа
Спектроскопические методы анализа Решения задач по теме Плавление и отвердевание кристаллических тел
Решения задач по теме Плавление и отвердевание кристаллических тел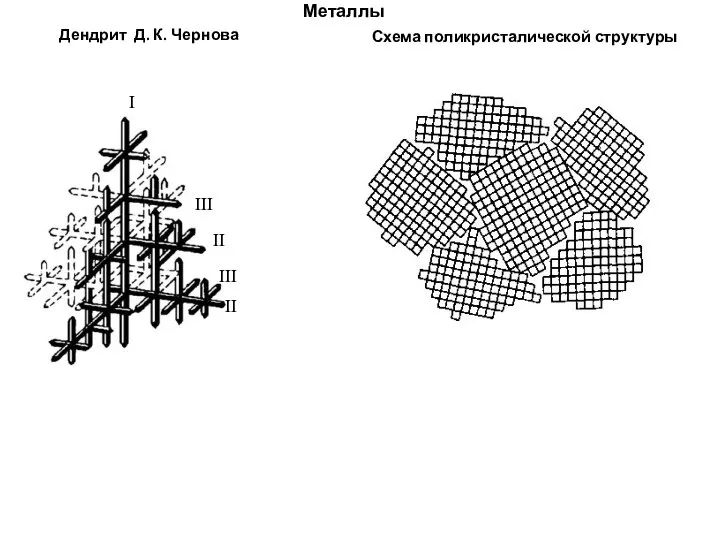 Металлы. Дендрит Д.К. Чернова
Металлы. Дендрит Д.К. Чернова Количество теплоты
Количество теплоты Методы инструментального выявления недостоверного учета электрической энергии
Методы инструментального выявления недостоверного учета электрической энергии Презентация на тему Оптические приборы
Презентация на тему Оптические приборы  Активация в ядерной физике. (Тема 2.8)
Активация в ядерной физике. (Тема 2.8)