Слайд 2Работа и кинетическая энергия

Слайд 3Работа и кинетическая энергия

Слайд 4Работа и кинетическая энергия
Рисунок поясняет выражение
Из рисунка видно, что элементарная работа

δА равна площади заштрихованной полоски, а работа А по перемещению из точки 1 в точку 2 – площади, ограниченной кривой, ординатами 1 и 2 и осью абсцисс.
При этом площадь фигуры над осью s берется со знаком плюс (она соответствует положительной работе), а площадь фигуры под осью абсцисс – со знаком минус
Слайд 5Работа и кинетическая энергия
Единицей работы в системе Си является джоуль (Дж).
Джоуль

есть работа силы в один ньютон на перемещении в один метр при условии, что направление силы совпадает с направлением перемещения.
Слайд 6Работа и кинетическая энергия

Слайд 7Работа и кинетическая энергия

Слайд 8Работа и кинетическая энергия

Слайд 9Работа и кинетическая энергия

Слайд 13Работа и кинетическая энергия
Если точки придут в движение, то каждая из сил

совершит положительную работу.
Будет положительной и работа обеих сил. Она пойдет на приращение кинетической энергии системы.
Следовательно, приращение кинетической энергии определяется работой не только внешних, но и внутренних сил.
Слайд 14Консервативные силы. Потенциальная энергия
Если в каждой точке пространства на помещенную туда частицу

действует сила, то говорят, что частица находится в поле сил.
Так, например, частица может находиться в поле
сил тяжести,
в поле упругих сил,
в поле сил сопротивления и т.д.
Слайд 15Консервативные силы. Потенциальная энергия
Существуют поля, в которых работа, совершаемая над частицей силами

поля, не зависит от пути, между точками 1 и 2.
Работа по замкнутому пути, естественно, в таких полях равна нулю.
Силы, обладающие такими свойствами, называются консервативными.
Слайд 16Консервативные силы. Потенциальная энергия
Все силы, не являющиеся консервативными, называют неконсервативными.
К их

числу относятся, например, силы трения и сопротивления среды.
Работа этих сил зависти от пути между начальным и конечным положением частицы и не равна нулю на любом замкнутом пути.
Слайд 17Консервативные силы. Потенциальная энергия
Если на систему частиц действуют только консервативные силы, то

можно для нее ввести понятие потенциальной энергии. Какое-либо произвольное положение системы условно примем за нулевое.
Работа, совершаемая консервативными силами из рассматриваемого положение в нулевое, называется потенциальной энергией системы
Работа консервативных сил не зависит от пути, поэтому потенциальная энергия системы U зависит только от ее координат.
Слайд 18Консервативные силы. Потенциальная энергия

Слайд 19Консервативные силы. Потенциальная энергия

Слайд 20Консервативные силы. Потенциальная энергия

Слайд 21Консервативные силы. Потенциальная энергия
Этот произвол не может отразиться на физических выводах, так

как ход физических явлений зависит не от абсолютных значений самой потенциальной энергии, а лишь от ее разности в различных состояниях.
Слайд 22Консервативные силы. Потенциальная энергия
Пусть система перешла из положения 1 в положение 2

по какому-нибудь пути 12 (рис. б).
Работу А12, совершенную консервативными силами при таком переходе, можно выразить через потенциальные энергии U1 и U2 в состояниях 1 и 2.
Слайд 23Консервативные силы. Потенциальная энергия
С этой целью вообразим, что переход осуществлен через нулевое

положение О, т.е. по пути 1О2.
Так как силы консервативны, то А12 = А1О2 = А1О + АО2 =А1О – А2О. По определению
Потенциальной энергии U1 = А1О +С, U2 = А2О +С, где С – одна и та же постоянная
Слайд 24Консервативные силы. Потенциальная энергия
Таким образом,
А12 = U1 – U2,
т.е. работа консервативных сил

равна убыли потенциальной энергии системы
Слайд 26Закон сохранения энергии
Сумма кинетической и потенциальной энергий системы называется ее полной энергией

Е. Таким образом Е1 = Е2, или
Е= К + U = const.
В системе с одними только консервативными силами полная энергия остается постоянной.
Слайд 27Закон сохранения энергии
Могут происходить только превращения из кинетической энергии в потенциальную и

обратно, но полный запас энергии системы измениться не может.
Это положение называется законом сохранения энергии в механике.
Слайд 28Потенциальная энергия и сила
Вычислим потенциальную энергию в некоторых простейших случаях.
а). Потенциальная энергия

тела в однородном поле тяжести.
Если материальная точка, находящаяся на высоте h, упадет на нулевой уровень, то сила тяжести совершит работу А = mgh.
Поэтому на высоте h материальная точка обладает потенциальной энергией U = mgh + C.
Слайд 29Потенциальная энергия и сила
За нулевой можно принять произвольный уровень, например, уровень пола,

уровень моря и т.д.
Постоянная С равна потенциальной энергии на нулевом уровне. Полагая ее равной нулю, получим
U = mgh
Слайд 30Потенциальная энергия и сила
б) Потенциальная энергия растянутой пружины.
Упругие силы, возникающие при

растяжении или сжатии пружины, консервативны.
Поэтому имеет смысл говорить о потенциальной энергии деформированной пружины.
Ее называют упругой энергией. Обозначим через x растяжение пружины, т.е. разность x = l – l0 длин пружин в деформированном и недеформированном состояниях.
Слайд 35Потенциальная энергия и сила
Как показывают приведенные примеры, зная зависимость сил от координат

можно путем интегрирования найти потенциальную энергию частицы.
Можно поставить и обратную задачу: вычислить действующие силы по заданной потенциальной энергии.
Эта задача решается с помощью дифференцирования
Слайд 37Абсолютно неупругий удар
Интересным примером, где имеет место потеря механической энергии под действием

диссипативных сил, является абсолютно неупругий удар.
Так называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно целое
Слайд 38Абсолютно неупругий удар
Скорость образовавшегося в результате столкновения тела можно найти, используя закон

сохранения импульса.
Пусть шары движутся вдоль прямой, соединяющей их центры, со скоростями v1 и v2 .
В этом случае говорят, что удар является центральным. Обозначим через v скорость образовавшегося тела
Слайд 41Абсолютно неупругий удар
Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря

кинетической энергии макроскопического движения, равная половине произведения приведенной массы на квадрат относительной скорости.
Слайд 44Абсолютно неупругий удар
Разрушительные эффекты при авариях, конечно, являются бедствием.
Но в некоторых

случаях, например при изучении превращений, претерпеваемых атомными ядрами и элементарными частицами во время столкновения, они являются целью исследования.
В таких случаях стремятся к тому, чтобы разрушительные эффекты усилить.
Слайд 51Абсолютно упругий удар
Получилось всего три уравнения для определения четырех неизвестных (скорости, помеченные

штрихами).
Чтобы написать недостающее уравнение, введем предположение, что при столкновении шаров не возникают тангенциальные силы.
Ввести такое предположение вынуждает нас закон сохранения энергии, уже использованный при написании наших уравнений.
Слайд 52Абсолютно упругий удар
Если бы при столкновении развивались тангенциальные силы трения скольжения, механическая

энергия не могла бы сохраняться. Поэтому, предполагая удар идеально упругим, мы должны считать сами шары идеально, гладкими.
При их столкновении тангенциальные силы не возникают.
Слайд 54Абсолютно упругий удар
При столкновении гладких идеально упругих шаров их тангенциальные скорости не

изменяются.
Нормальные же скорости изменяются так же, как и скорости при центральном ударе.
В частности, при столкновениях не изменяются состояния вращения шаров.
Если шары одинаковы, то при столкновении они обмениваются нормальными скоростями, тангенциальные скорости их остаются неизменными.
Слайд 55Задача
Частица массой m налетает на покоящуюся частицу со скоростью v1 и после

абсолютно упругого удара отлетает со скоростью v2 перпендикулярно к направлению своего первоначального движения. Найти массу частицы M.
































































 Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки Колебательное движение (9 класс)
Колебательное движение (9 класс) Юные астрофизики
Юные астрофизики АЭС_1663630896
АЭС_1663630896 Удивительный транспорт
Удивительный транспорт Опыты с водой: сильный газ и остуди пар
Опыты с водой: сильный газ и остуди пар Физика – это наука понимать природу…
Физика – это наука понимать природу… Виды соединения проводников. Работа тока
Виды соединения проводников. Работа тока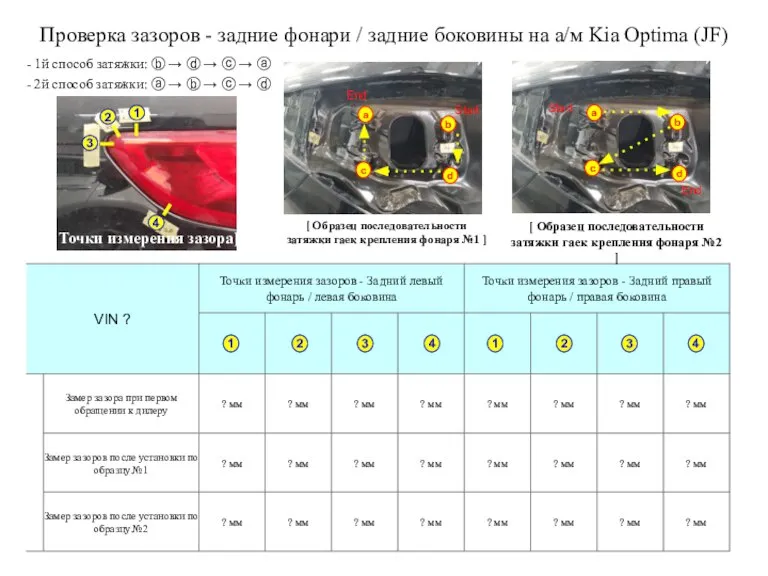 Проверка зазоров - задние фонари / задние боковины на а/м Kia Optima (JF)
Проверка зазоров - задние фонари / задние боковины на а/м Kia Optima (JF) Презентация на тему Вклад отечественной физики в Великую Победу
Презентация на тему Вклад отечественной физики в Великую Победу  Механические передачи и их применение
Механические передачи и их применение Определение высоты отскока шарика для настольного тенниса. Превращение и сохранение энергии. 7 класс
Определение высоты отскока шарика для настольного тенниса. Превращение и сохранение энергии. 7 класс Энтропия и развитие Вселенной
Энтропия и развитие Вселенной Давление твердых тел
Давление твердых тел Световые явления. 8 класс
Световые явления. 8 класс Электростатическое поле в диэлектрике. Лекция 3-2020
Электростатическое поле в диэлектрике. Лекция 3-2020 Модельный ряд двигателей ЗМЗ
Модельный ряд двигателей ЗМЗ Закон всемирного тяготения
Закон всемирного тяготения Стихотворение Ученье - свет, а не ученье - тьма
Стихотворение Ученье - свет, а не ученье - тьма Экспериментальные методы исследования частиц
Экспериментальные методы исследования частиц Путешествие в мир силы тяжести
Путешествие в мир силы тяжести L2_1_Mekhanicheskie_kharakteristiki_metallov
L2_1_Mekhanicheskie_kharakteristiki_metallov Оборудование понизительных подстанций
Оборудование понизительных подстанций Презентация на тему Радиоактивные превращения атомных ядер (9 класс)
Презентация на тему Радиоактивные превращения атомных ядер (9 класс)  Радиация
Радиация Определение скорости движения условной лодки по силе сопротивления при работе на тренажере
Определение скорости движения условной лодки по силе сопротивления при работе на тренажере Продукты питания в руках физикаa
Продукты питания в руках физикаa Формирование атома
Формирование атома