Содержание
- 2. А.С. Чуев - 2020 Мир каждый видит в облике ином, и каждый прав – так много
- 3. Математическое описание полей подробно изучить самостоятельно А.С. Чуев - 2020
- 4. А.С. Чуев - 2020
- 5. А.С. Чуев - 2020
- 6. Скалярное и векторное поле А.С. Чуев - 2020
- 7. Описание свойств векторных полей А.С. Чуев - 2020
- 8. А.С. Чуев - 2020 Понятие производной по направлению
- 9. А.С. Чуев - 2020
- 10. А.С. Чуев - 2020
- 11. Чуев: Дивергенция – это изменение вектора в своем собственном направлении (по модулю) Определения дивергенции. Второе считается
- 12. А.С. Чуев - 2020
- 13. А.С. Чуев - 2020
- 14. А.С. Чуев - 2020
- 15. А.С. Чуев - 2020 РОТОР И ЦИРКУЛЯЦИЯ
- 16. РОТОР И ЦИРКУЛЯЦИЯ Какой вектор первичен A или rotA? А.С. Чуев - 2020
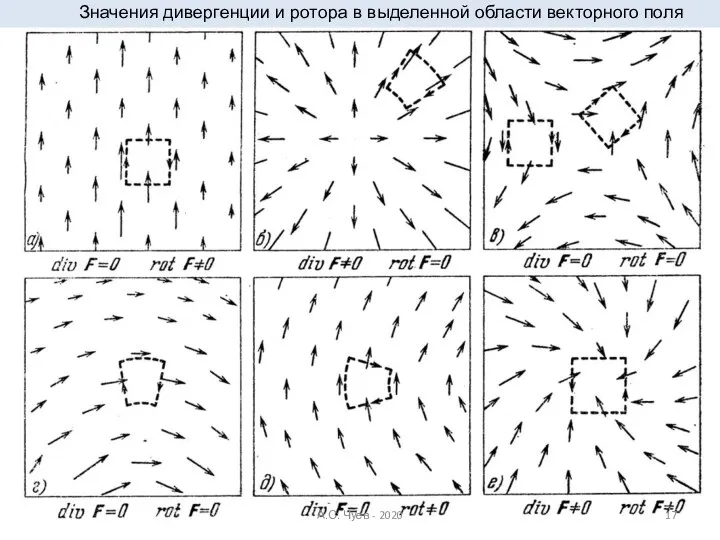
- 17. Значения дивергенции и ротора в выделенной области векторного поля А.С. Чуев - 2020
- 18. Работа в потенциальном поле по перемещению электрического заряда Работа электростатических сил не зависит от формы пути,
- 19. Интеграл от вектора по замкнутому контуру называется циркуляцией этого вектора. Работа по замкнутому контуру в потенциальном
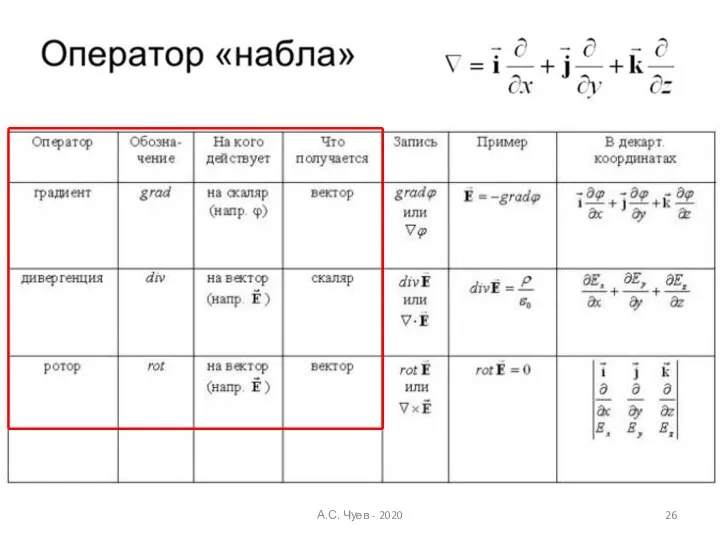
- 20. Напряженность в векторной форме: - оператор «набла» (оператор Гамильтона) Это вектор! А.С. Чуев - 2020
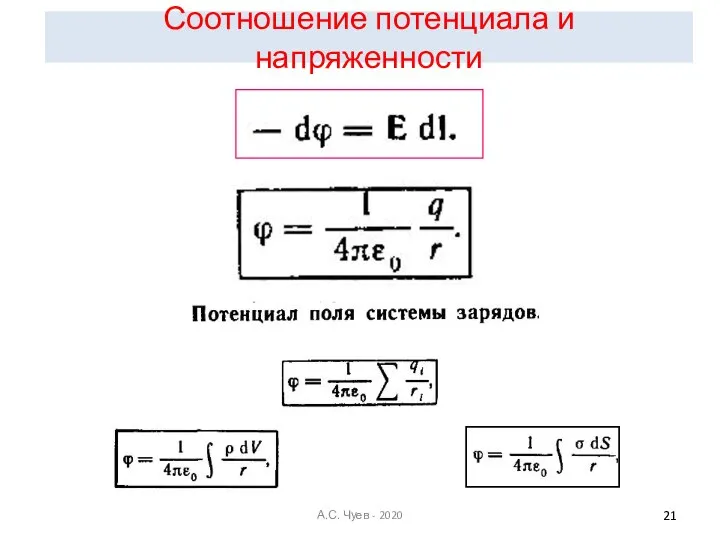
- 21. Соотношение потенциала и напряженности А.С. Чуев - 2020
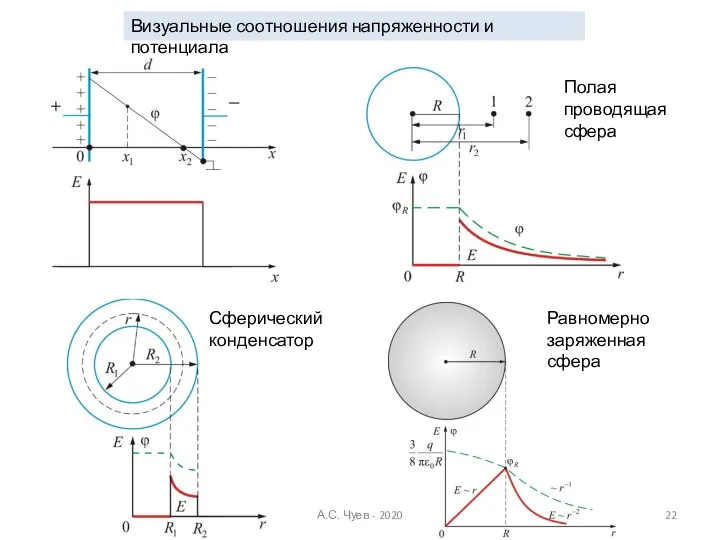
- 22. Визуальные соотношения напряженности и потенциала Полая проводящая сфера Равномерно заряженная сфера Сферический конденсатор А.С. Чуев -
- 23. Из учебника Савельева Другое определение дивергенции А.С. Чуев - 2020
- 24. А.С. Чуев - 2020
- 25. А.С. Чуев - 2020 Связь напряженности и потенциала Общая формула для дивергенции Дивергенция вектора Е
- 26. А.С. Чуев - 2020
- 27. Теорема Гаусса в дифференциальной форме (в вакууме). Уравнение Пуассона А.С. Чуев - 2020 Уравнение Пуассона
- 28. Уравнение Пуассона в иной форме записи Уравнение Лапласа: А.С. Чуев - 2020
- 29. А.С. Чуев - 2020 В потенциальном электрическом поле rotE = 0 В однородном электрическом поле grad
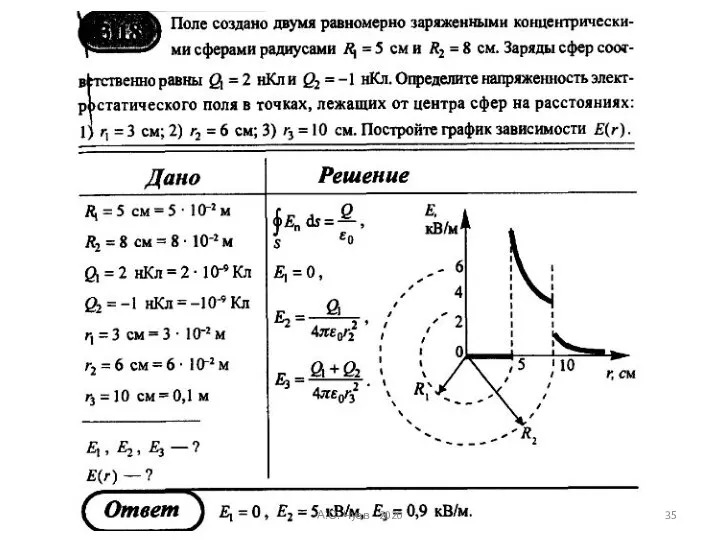
- 30. Примеры на теорему Гаусса А.С. Чуев - 2020
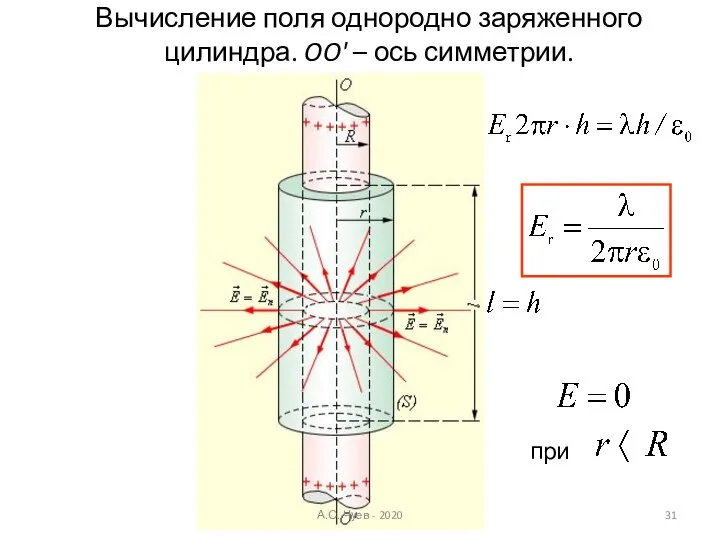
- 31. Вычисление поля однородно заряженного цилиндра. OO' – ось симметрии. при А.С. Чуев - 2020
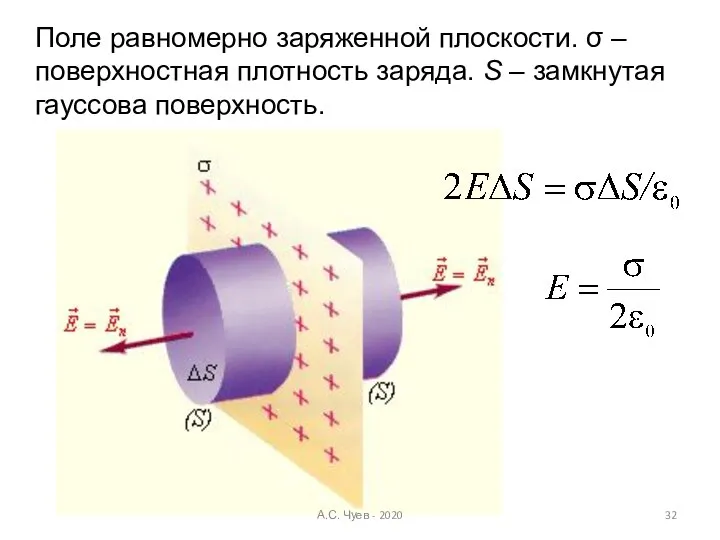
- 32. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность. А.С. Чуев
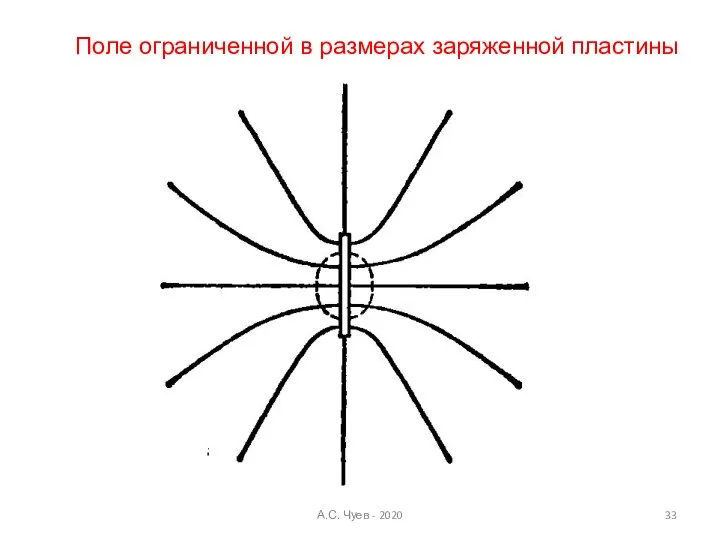
- 33. А.С. Чуев - 2020 Поле ограниченной в размерах заряженной пластины
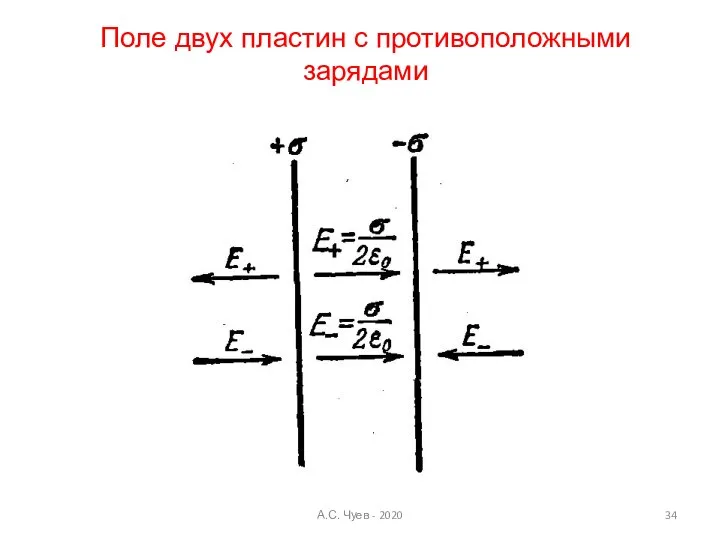
- 34. А.С. Чуев - 2020 Поле двух пластин с противоположными зарядами
- 35. А.С. Чуев - 2020
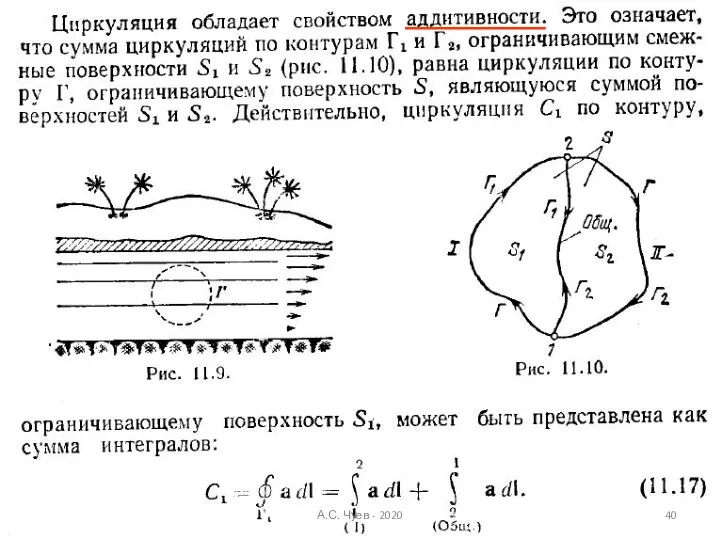
- 36. Подробнее о циркуляция вектора напряженности А.С. Чуев - 2020
- 37. Полезная информация о циркуляции вектора (из учебника Савельева) А.С. Чуев - 2020
- 38. А.С. Чуев - 2020
- 39. А.С. Чуев - 2020
- 40. А.С. Чуев - 2020
- 41. А.С. Чуев - 2020
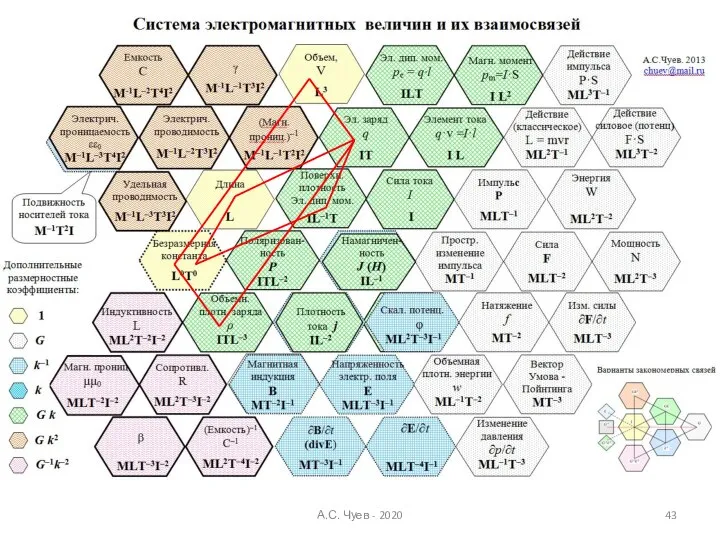
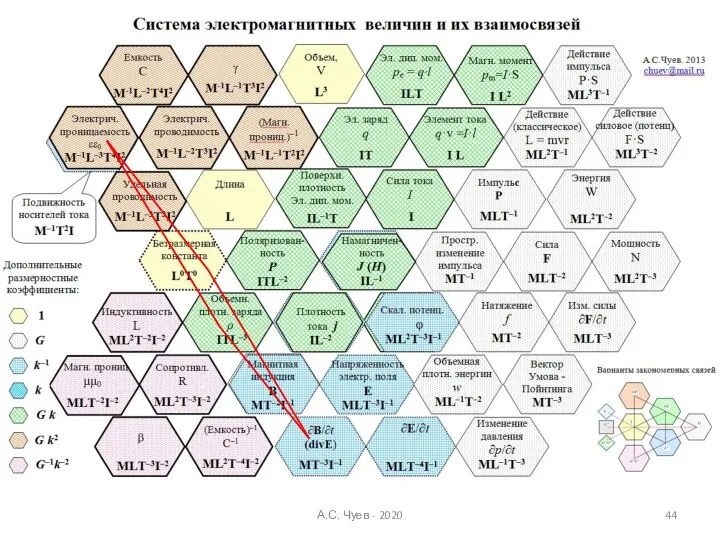
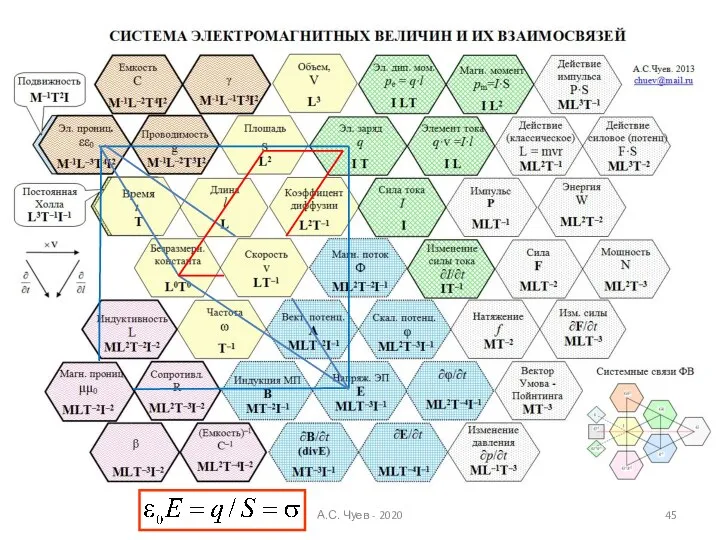
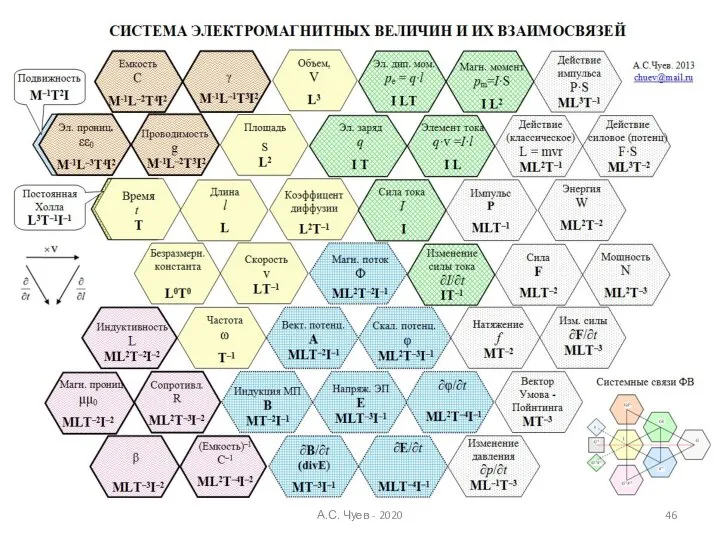
- 42. Примеры поиска закономерных соотношений ФВ А.С. Чуев - 2020
- 43. А.С. Чуев - 2020
- 44. А.С. Чуев - 2020
- 45. А.С. Чуев - 2020
- 46. А.С. Чуев - 2020
- 48. Скачать презентацию































 Физика пластической деформации кристаллов
Физика пластической деформации кристаллов Динамика. Лекция 8
Динамика. Лекция 8 Vztah mezi napětím a deformací fyzikální rovnice
Vztah mezi napětím a deformací fyzikální rovnice Электрическая цепь
Электрическая цепь Волновые свойства частиц
Волновые свойства частиц Закон Максвелла. Электромагнитное поле
Закон Максвелла. Электромагнитное поле Обобщающий урок по теме Электрический ток
Обобщающий урок по теме Электрический ток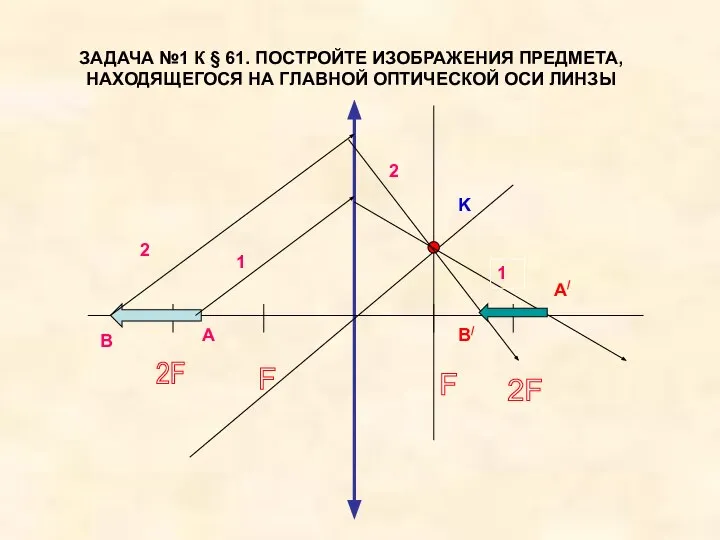 Построения в линзе
Построения в линзе Закон Всемирного тяготения
Закон Всемирного тяготения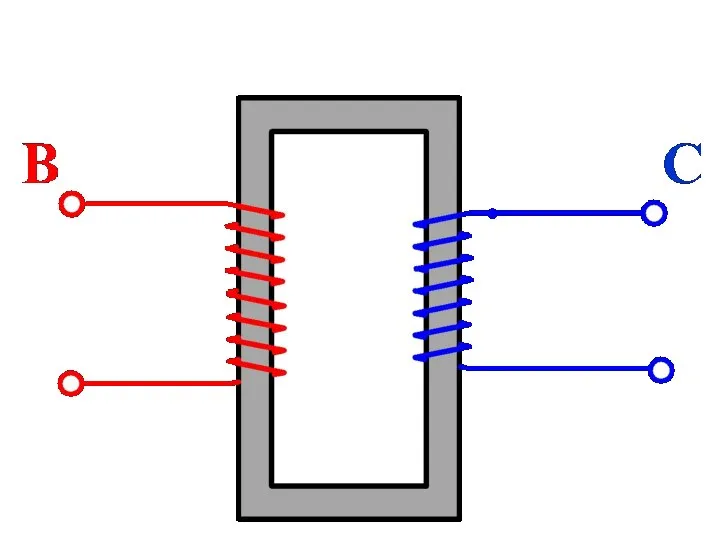 Автотрансформаторы
Автотрансформаторы Технология обработки на металлорежущих станках. Устройство делительных головок
Технология обработки на металлорежущих станках. Устройство делительных головок Урок 16 Підготовка до контрольної роботи
Урок 16 Підготовка до контрольної роботи Направление и пределы самопроизвольного протекания физико-химических процессов
Направление и пределы самопроизвольного протекания физико-химических процессов Трехфазные электрические цепи переменного тока
Трехфазные электрические цепи переменного тока Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа №1
Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа №1 Последовательное соединение проводников
Последовательное соединение проводников Урок 22. Повторение. Законы Ньютона. Решение задач
Урок 22. Повторение. Законы Ньютона. Решение задач Плотность вещества
Плотность вещества Атомная кузница кадров
Атомная кузница кадров Законы сохранения
Законы сохранения Квантовые технологии
Квантовые технологии Приводные муфты
Приводные муфты Радиоактивность. Открытие
Радиоактивность. Открытие Морской бой. Игра по физике
Морской бой. Игра по физике Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Сверхпроводимость материалов
Сверхпроводимость материалов Гидростатическое давление
Гидростатическое давление Презентация на тему Экономия использования энергетических ресурсов на земле
Презентация на тему Экономия использования энергетических ресурсов на земле