Содержание
- 2. ПРОДОЛЬНЫЙ ИЗГИБ. УСТОЙЧИВОСТЬ 2
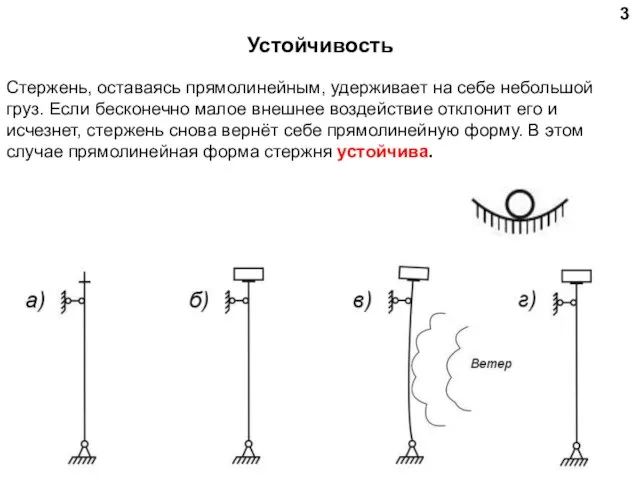
- 3. 3 Устойчивость Стержень, оставаясь прямолинейным, удерживает на себе небольшой груз. Если бесконечно малое внешнее воздействие отклонит
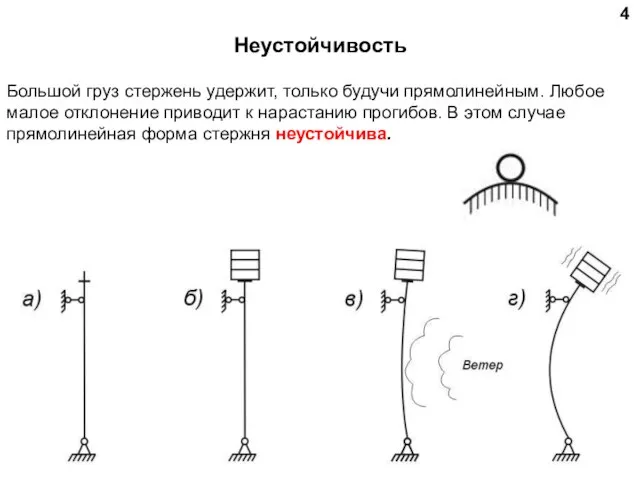
- 4. 4 Большой груз стержень удержит, только будучи прямолинейным. Любое малое отклонение приводит к нарастанию прогибов. В
- 5. 5 Состояние безразличного равновесия Между устойчивым и неустойчивым состояниями существует состояние безразличного равновесия: груз можно подобрать
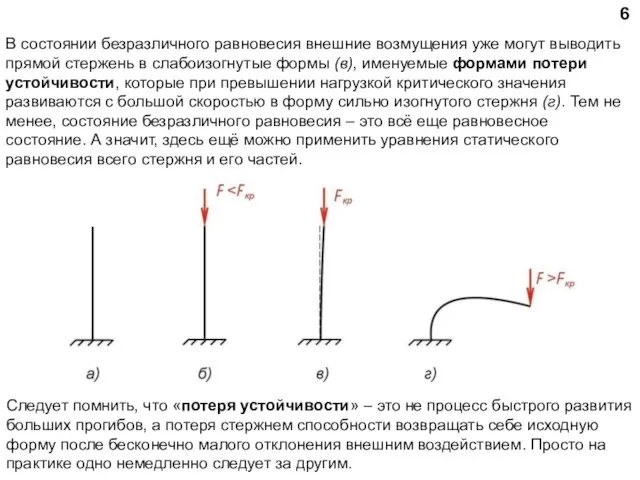
- 6. 6 В состоянии безразличного равновесия внешние возмущения уже могут выводить прямой стержень в слабоизогнутые формы (в),
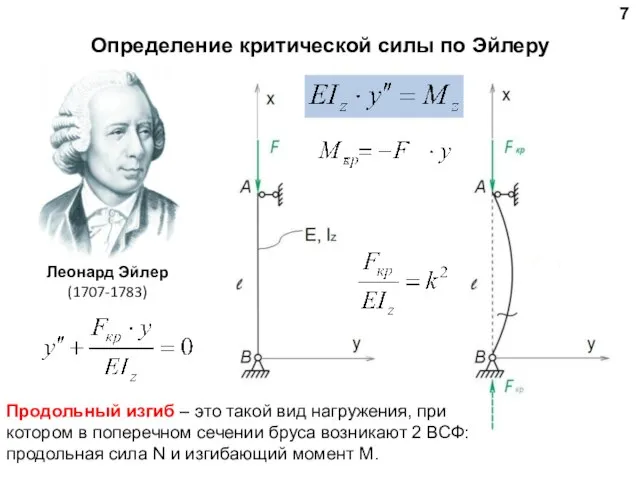
- 7. 7 Определение критической силы по Эйлеру Леонард Эйлер (1707-1783) Продольный изгиб – это такой вид нагружения,
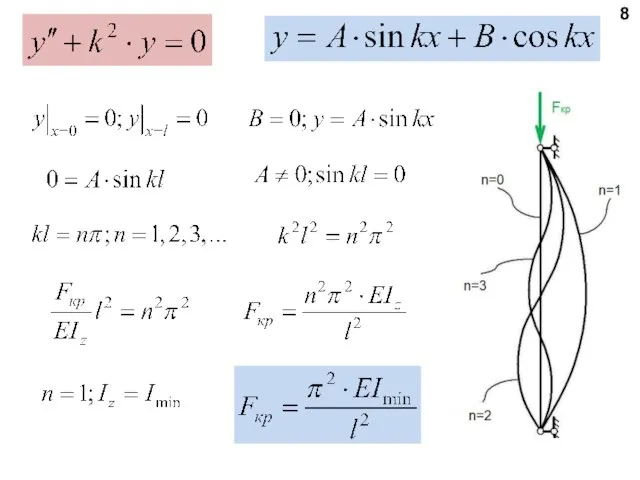
- 8. 8
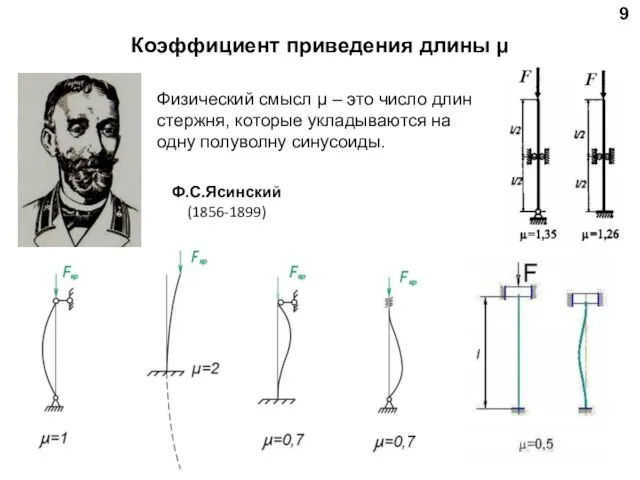
- 9. 9 Коэффициент приведения длины μ Физический смысл μ – это число длин стержня, которые укладываются на
- 10. 10 Поскольку формула Эйлера выводилась из приближенного дифференциального уравнения упругой линии балки, она является приближенной. Поскольку
- 11. 11 Формула Ясинского: Ст. 3: а = 310 МПа; b = 1,14 МПа. Сосна: а =
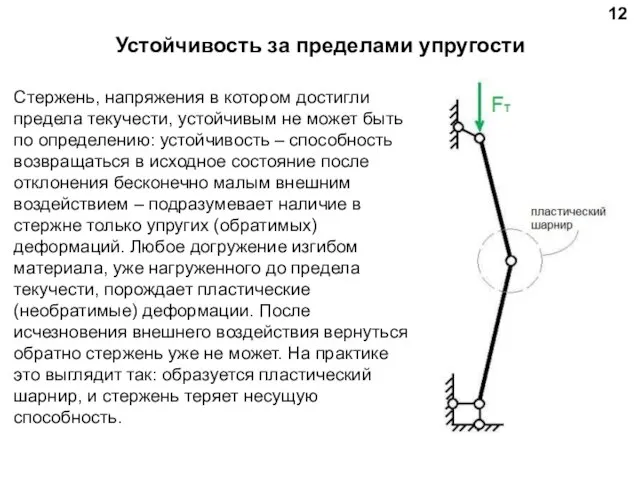
- 12. 12 Стержень, напряжения в котором достигли предела текучести, устойчивым не может быть по определению: устойчивость –
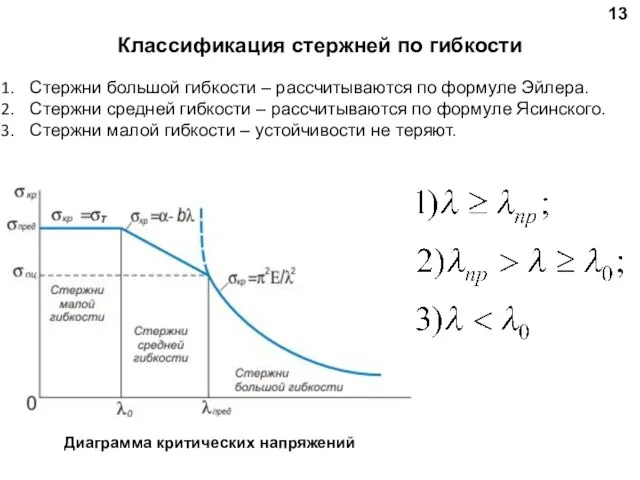
- 13. 13 Классификация стержней по гибкости Стержни большой гибкости – рассчитываются по формуле Эйлера. Стержни средней гибкости
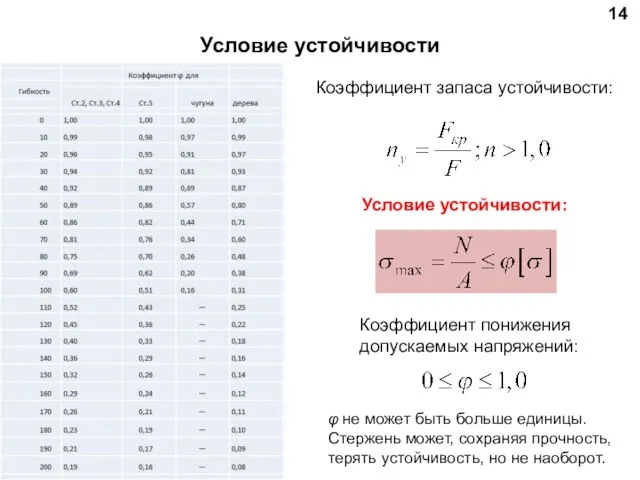
- 14. 14 φ не может быть больше единицы. Стержень может, сохраняя прочность, терять устойчивость, но не наоборот.
- 16. Скачать презентацию




 Эрнест Резерфорд
Эрнест Резерфорд История нанотехнологий. Лекция 2
История нанотехнологий. Лекция 2 Сила трения. Ответы к заданию №1
Сила трения. Ответы к заданию №1 Планета Воды
Планета Воды Теоретическая механика. Кинематика. Движение твердой среды
Теоретическая механика. Кинематика. Движение твердой среды Презентация на тему Законы постоянного тока
Презентация на тему Законы постоянного тока 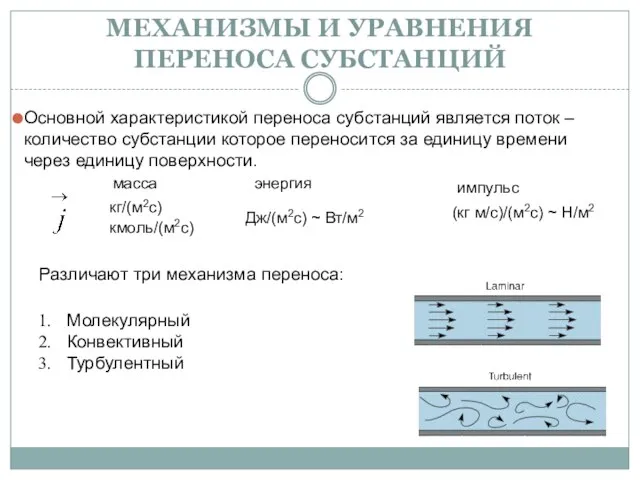 Механизмы и уравнения переноса субстанций
Механизмы и уравнения переноса субстанций Электричество и магнетизм (лекция 11)
Электричество и магнетизм (лекция 11) Закон Ома для участка цепи
Закон Ома для участка цепи Ядерная бомба
Ядерная бомба Теоретическая механика. Модуль 1. Раздел 3 – динамика точки
Теоретическая механика. Модуль 1. Раздел 3 – динамика точки Решение задач на движение частицы в магнитном поле
Решение задач на движение частицы в магнитном поле Фотоны. Давление света. Корпускулярно-волновой дуализм
Фотоны. Давление света. Корпускулярно-волновой дуализм Мощность. Единицы мощности
Мощность. Единицы мощности Решение задач репетиционного тестирования по физике, этап 1
Решение задач репетиционного тестирования по физике, этап 1 Физика и В.О.В
Физика и В.О.В Пользуйтесь энергосберегающими приборами
Пользуйтесь энергосберегающими приборами Презентация на тему Применение конденсаторов
Презентация на тему Применение конденсаторов  Пример построения наблюдателя для системы 3-го порядка
Пример построения наблюдателя для системы 3-го порядка Лекция_0_1
Лекция_0_1 Закон Ома и вычисление сопротивления. Решение задач
Закон Ома и вычисление сопротивления. Решение задач Связи. Реакции связей. Основные понятия
Связи. Реакции связей. Основные понятия Презентация на тему Влияние шума и музыки на здоровье человека
Презентация на тему Влияние шума и музыки на здоровье человека  Фотометрия Бугера, Ламберта, Бера
Фотометрия Бугера, Ламберта, Бера Физическая лихорадка. Методические указания
Физическая лихорадка. Методические указания Приходченко ФЕР-2032и
Приходченко ФЕР-2032и Георг Ом (1787-1854) немецкий физик
Георг Ом (1787-1854) немецкий физик Рівновага складеної системи сил
Рівновага складеної системи сил