Содержание
- 2. Статически неопределимый брус (стержень) Дан стержень, жестко закрепленный с двух концов и нагруженный силами Р1 и
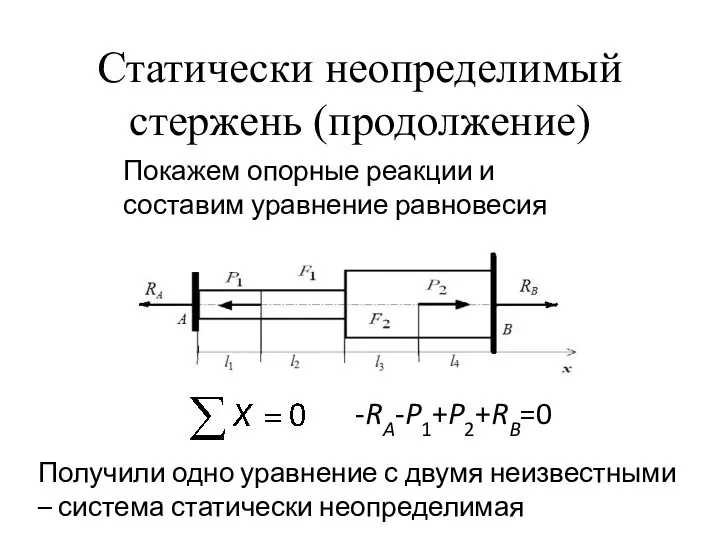
- 3. Статически неопределимый стержень (продолжение) Покажем опорные реакции и составим уравнение равновесия -RA-P1+P2+RB=0 Получили одно уравнение с
- 4. Раскрытие статической неопределимости Для раскрытия статической неопределимости осуществляется переход к статически определимому стержню, эквивалентному заданному, путем
- 5. Есть два подхода к записи уравнения перемещений UB=0. Первый рассматривает перемещение UB как сумму накопленных деформаций
- 6. Определение внутренних силовых факторов на каждом участке и запись уравнения перемещений
- 7. Второй подход к записи уравнения перемещений UB=0. Используется принцип независимости действия сил где
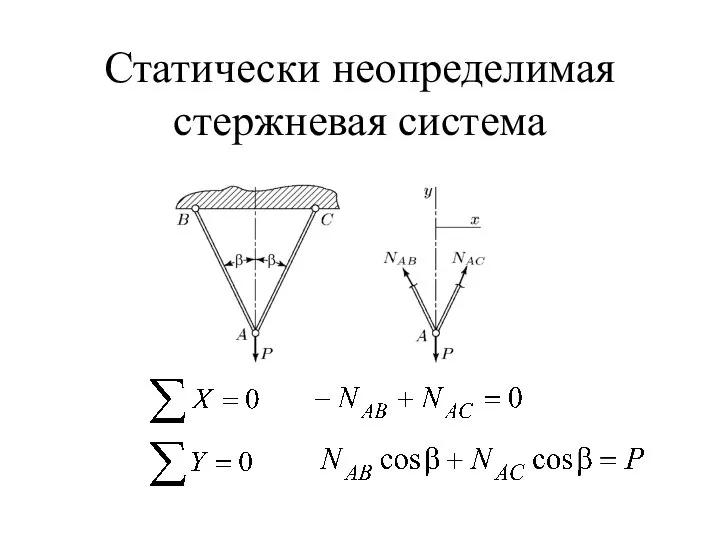
- 8. Статически неопределимая стержневая система ; .
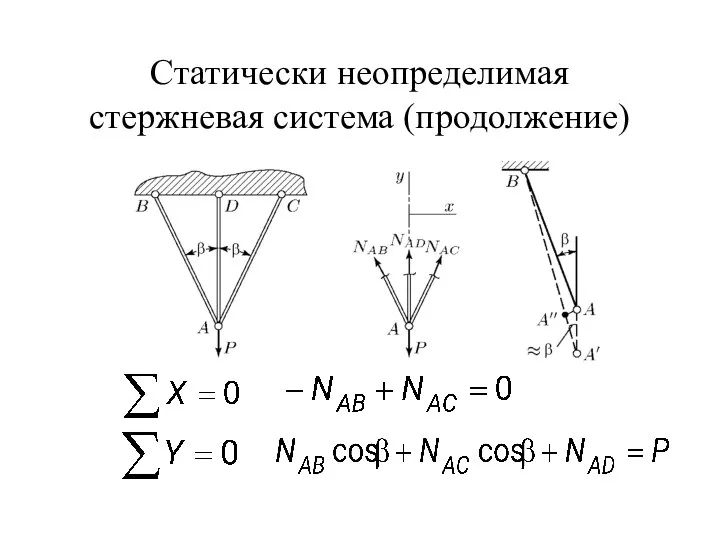
- 9. Статически неопределимая стержневая система (продолжение) .
- 10. Статически неопределимая стержневая система (продолжение 2) .
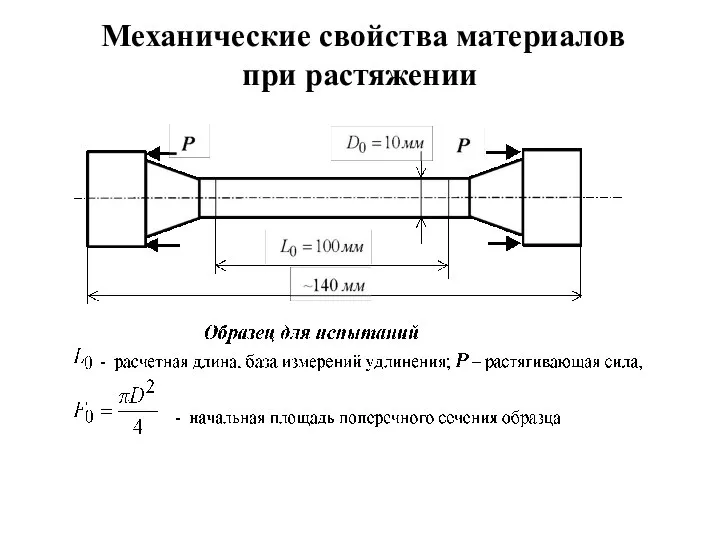
- 11. Механические свойства материалов при растяжении
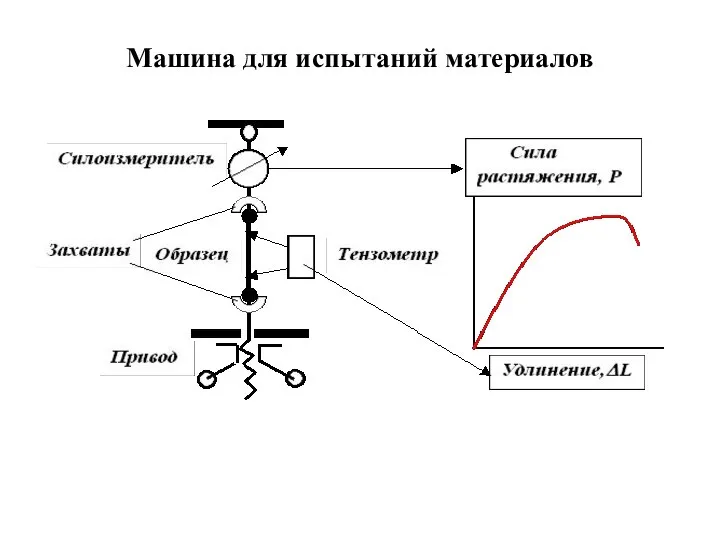
- 12. Машина для испытаний материалов
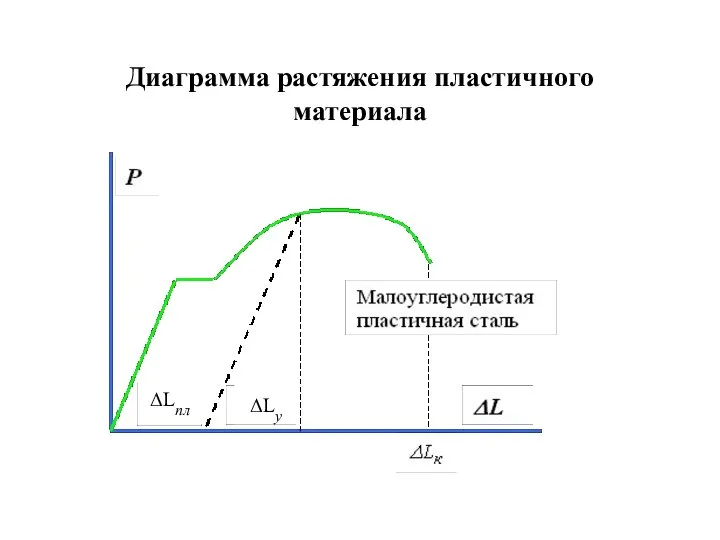
- 13. Диаграмма растяжения пластичного материала ΔLпл ΔLу
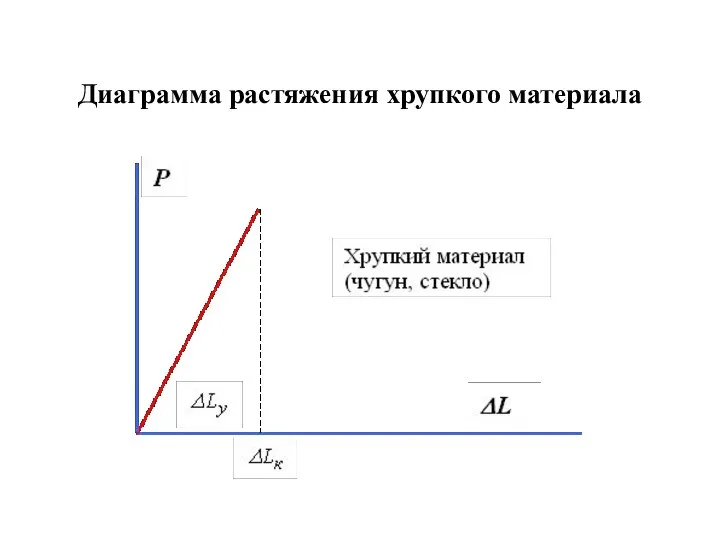
- 14. Диаграмма растяжения хрупкого материала
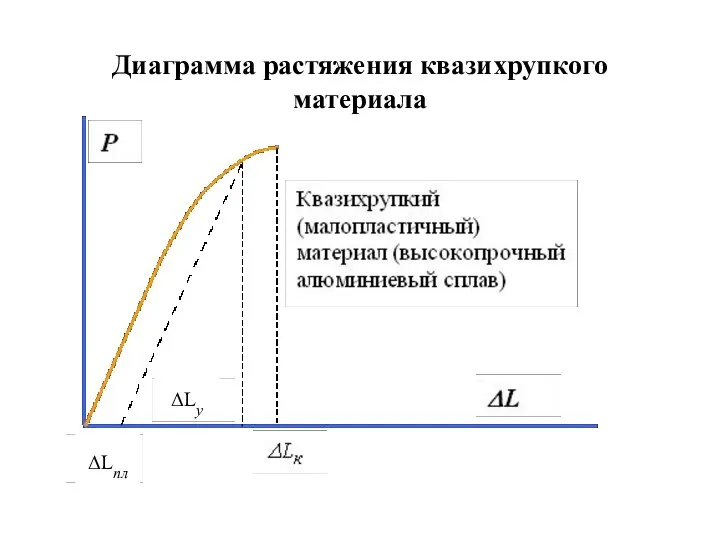
- 15. Диаграмма растяжения квазихрупкого материала ΔLпл ΔLу
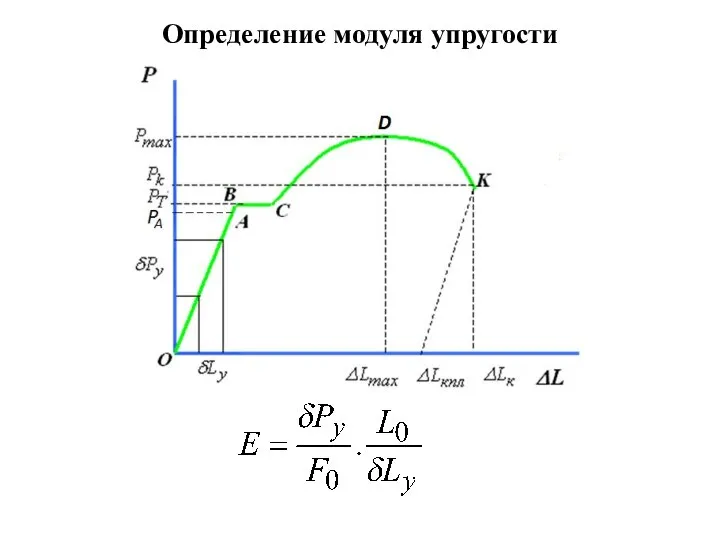
- 16. Определение модуля упругости
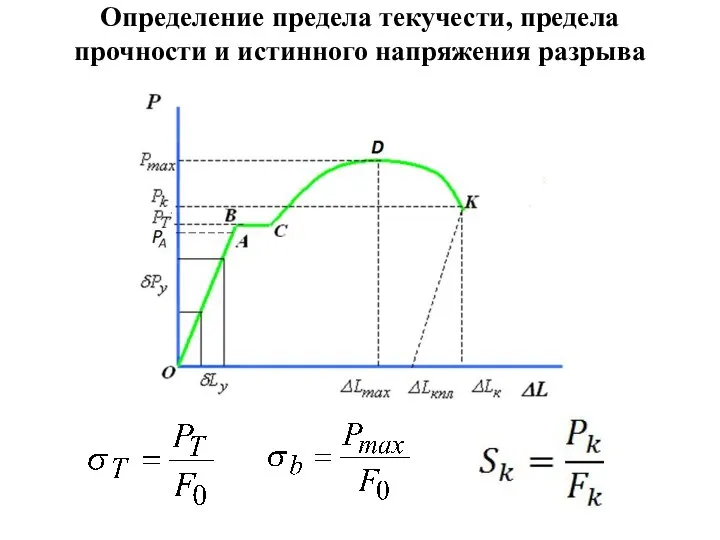
- 17. Определение предела текучести, предела прочности и истинного напряжения разрыва
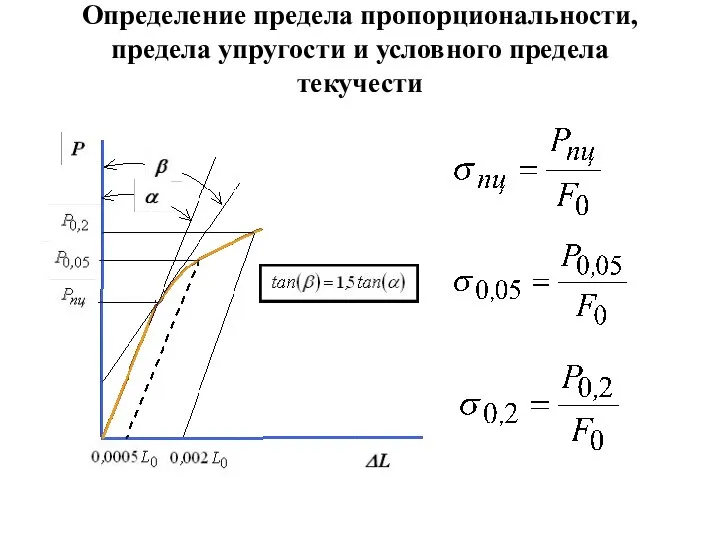
- 18. Определение предела пропорциональности, предела упругости и условного предела текучести
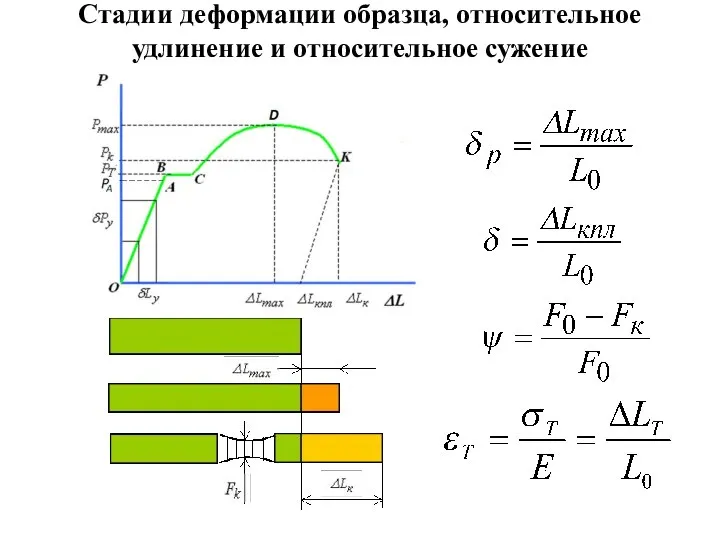
- 19. Стадии деформации образца, относительное удлинение и относительное сужение
- 20. Предельные характеристики материалов Предел текучести для пластичных материалов - σ Временное сопротивление или предел прочности для
- 21. Жесткость и податливость стержня
- 22. Испытание на сжатие Особенности испытания на сжатие Трудно обеспечить соосность нагружения Длинные образцы теряют устойчивость Чем
- 23. Механические характеристики, определяемые при испытании хрупких и пластичных материалов на сжатие по ГОСТ 25.503 ГОСТом предусматривается
- 24. Механические характеристики, определяемые при испытании хрупких и пластичных материалов на сжатие по ГОСТ 25.503 По результатам
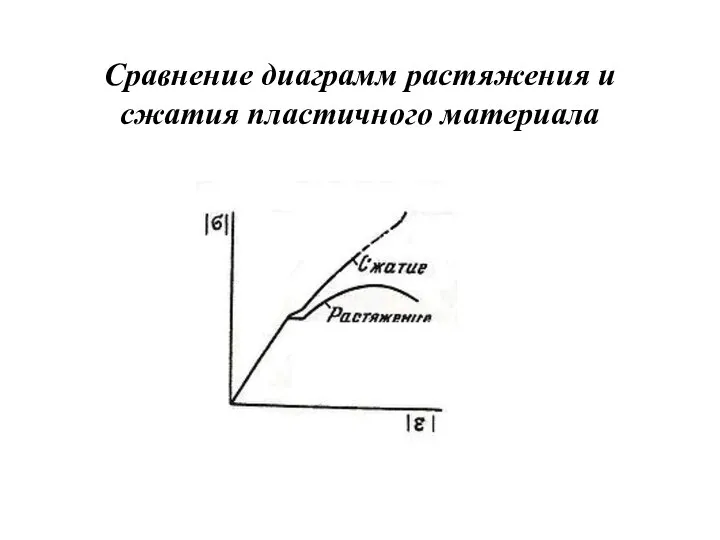
- 25. Сравнение диаграмм растяжения и сжатия пластичного материала
- 26. Сравнение диаграмм растяжения и сжатия пластичного материала При развитых пластических деформациях вид кривой сжатия существенно отличается
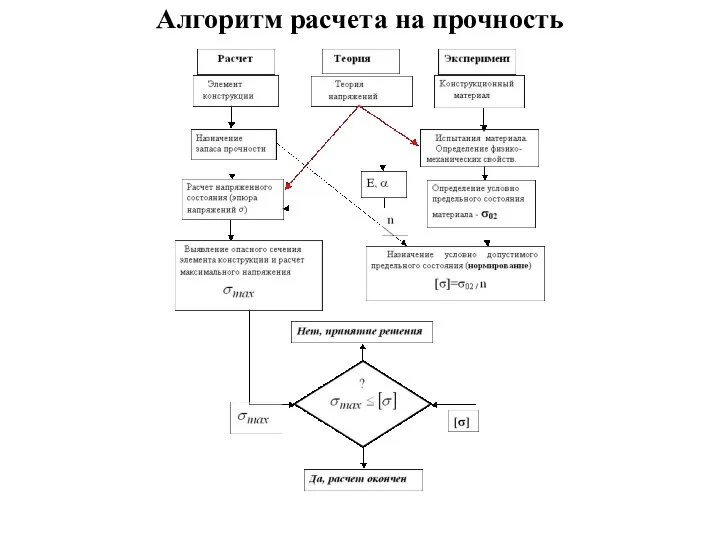
- 27. Алгоритм расчета на прочность
- 29. Скачать презентацию












 Калибровка средств измерений (Тема 3)
Калибровка средств измерений (Тема 3) Лабораторная работа №2 Измерение размеров малых тел
Лабораторная работа №2 Измерение размеров малых тел Презентация на тему Закон сохранения энергии в тепловых процессах
Презентация на тему Закон сохранения энергии в тепловых процессах  Управление электродвигателем в заданной последовательности
Управление электродвигателем в заданной последовательности Техническое обслуживание и ремонт заднего моста автомобиля ГАЗ 31105. Экзаменационная работа
Техническое обслуживание и ремонт заднего моста автомобиля ГАЗ 31105. Экзаменационная работа III Инженерная олимпиада им.Н.А.Зайцева
III Инженерная олимпиада им.Н.А.Зайцева Презентация на тему Активные фильтры
Презентация на тему Активные фильтры  Свет. Свойства света
Свет. Свойства света Физические свойства веществ при низких температурах. Свойства криогенных жидкостей
Физические свойства веществ при низких температурах. Свойства криогенных жидкостей Условия плавания тел
Условия плавания тел 1_kurs_2_nedelya (1)
1_kurs_2_nedelya (1) Основные понятия фотометрии
Основные понятия фотометрии Pr
Pr Работа сил тяжести и упругости. Потенциальная энергия
Работа сил тяжести и упругости. Потенциальная энергия Проект Прорыв – создание Опытно-демонстрационного энергокомплекса
Проект Прорыв – создание Опытно-демонстрационного энергокомплекса Силы в природе Выполнил ученик 7 «А» класса Лабутин Никита, руководитель учитель физики Братушка А.Д.
Силы в природе Выполнил ученик 7 «А» класса Лабутин Никита, руководитель учитель физики Братушка А.Д. Теоретическая механика
Теоретическая механика История открытия атома
История открытия атома Презентация на тему Энергосбережение в быту (8 класс)
Презентация на тему Энергосбережение в быту (8 класс)  Физика атомного ядра и элементарных частиц
Физика атомного ядра и элементарных частиц Физика – это наука о природе
Физика – это наука о природе Физический поезд в страну Давление. Урок – соревнование 7 класс
Физический поезд в страну Давление. Урок – соревнование 7 класс Презентация на тему Давление твёрдых тел
Презентация на тему Давление твёрдых тел  Циклирование фазы
Циклирование фазы Тепловые явления
Тепловые явления Единицы напряжения
Единицы напряжения Неньютоновская жидкость
Неньютоновская жидкость Где живет электричество? 8 класс
Где живет электричество? 8 класс