Слайд 4Распределение Максвелла
Закон распределения молекул по скоростям был получен в конце 19 века

Максвеллом.
При этом он сделал два предположения:
1. все направления скоростей равновероятны
2. рассчитанное с помощью закона распределения давление идеального газа должно соответствовать полученному из экспериментов уравнению.
Слайд 34Молекулярные пучки (потоки)
Надем поток молекул в вакуум через малое отверстие в стенке

сосуда. Если размер отверстия много меньше длины свободного пробега молекул, то столкновений в отверстии не будет, а концентрация молекул будет возмущена в области порядка размера отверстия.
Слайд 41Закон равнораспределения энергии по степеням свободы

Слайд 42Закон равнораспределения энергии по степеням свободы
Если молекула состоит из нескольких атомов, появляется

энергия связанная с её вращением и колебаниями атомов относительно равновесного положения. С этими движениями также будет связана соответствующая энергия.
Рассмотрим эту ситуацию на примере двухатомной молекулы
Слайд 43Закон равнораспределения энергии по степеням свободы
Момент инерции Iz =0 и энергия вращения

вокруг этой оси равна нулю. Можно показать, что средняя энергия связанная с вращениями по осям X и Y будет kT/2 на каждую ось. Для двухатомной молекулы , энергия вращения равна kT. Тот же самый результат мы получим для трехатомной линейной молекулы (молекула СО2)
Слайд 44Закон равнораспределения энергии по степеням свободы

Слайд 45Закон равнораспределения энергии по степеням свободы

Слайд 46Закон равнораспределения энергии по степеням свободы

Слайд 52Барометрическая формула
Для условий земной атмосферы h0 ≈ 10 км. Сооружаемые емкости имеют

значительно меньшие габариты, поэтому неоднородность распределения паров в них не наблюдается. Лишь при подъеме в горы или с помощью авиации обнаруживается влияние поля тяжести на распределение воздуха в атмосфере.
Слайд 54Барометрическая формула
Воздух представляет собой смесь газов, молекулы которых имеют различную массу. Состав

атмосферы должен резко изменяться с высотой. Относительная концентрация легких газов должна увеличиваться с высотой. Измерения состава воздуха на разных высотах не подтвердили этого вывода. Интенсивная конвекция в пределах тропосферы приводит к известному выравниванию состава воздуха по высоте. Общеизвестно также падение температуры с высотой.
Слайд 57Распределение Больцмана
Это распределение может использоваться для произвольного типа взаимодействия (то есть не

обязательно гравитационного) и для любого вида пространственной зависимости потенциальной энергии (то есть не обязательно приводящей к однородному внешнему полю).
Единственным ограничением является консервативный характер действующих сил – то есть это такие силы, для которых их работа при движению по замкнутому контуру равняется нулю. Только для таких сил можно ввести потенциальную энергию, которая зависит только от положения в пространстве.
Слайд 59Центрифугирование, разделение изотопов
Центрифугирование нашло широкое применение в химии и биологии как эффективный

способ разделения близких по молекулярному весу или плотности веществ. В системе отсчета, связанной с центрифугой, объект исследования находится в равновесии, и к нему можно применить распределение Больцмана.
Слайд 60Центрифугирование, разделение изотопов

Слайд 61Центрифугирование, разделение изотопов

Слайд 62Центрифугирование, разделение изотопов
Из формулы следует, что концентрация тяжелых частиц у боковой стенки

центрифуги относительно выше, что используется для разделения смесей. Сейчас особенно активно центрифугирование используется для разделения составляющих различных биологических препаратов. Также центрифугирование было использовано для обогащения урана. Уран состоит в основном из двух изотопов 238U (99,28 % природного содержания) и 235U (0,71 %). Cпособностью к ядерным реакциям деления обладает только изотоп 235U. Возникающая задача обогащения урана решалась путем его фторирования, с образованием газообразного соединения UF6, и последующего многократного центрифугирования























































 Механические передачи. Виды передач. Расчет передаточных отношений
Механические передачи. Виды передач. Расчет передаточных отношений Клепаные и сварные соединения
Клепаные и сварные соединения Презентация на тему Колебания
Презентация на тему Колебания  Кинематика точки. Лекция 5
Кинематика точки. Лекция 5 Расширение воздуха при нагревании
Расширение воздуха при нагревании Транспортные машины
Транспортные машины Физика звукоизоляции
Физика звукоизоляции Механика. Обобщающий урок. 10 класс
Механика. Обобщающий урок. 10 класс Бури. Скорость бури
Бури. Скорость бури Обслуживание машин Toyota
Обслуживание машин Toyota Классическая теория электропроводности. Законы постоянного тока. Лекция № 13
Классическая теория электропроводности. Законы постоянного тока. Лекция № 13 Презентация на тему Закон Паскаля
Презентация на тему Закон Паскаля  Решение задач по теме Основы термодинамики
Решение задач по теме Основы термодинамики Электромагнитное поле. История открытия. Компьютер как источник переменного электромагнитного поля
Электромагнитное поле. История открытия. Компьютер как источник переменного электромагнитного поля Бипризма Френеля
Бипризма Френеля Термодинамика. Внутренняя энергия
Термодинамика. Внутренняя энергия Электрический ток в газах
Электрический ток в газах Электрическое поле. Лекция № 1
Электрическое поле. Лекция № 1 Емкость
Емкость Наблюдение за состоянием колесных пар пассажирского вагона в пути следования
Наблюдение за состоянием колесных пар пассажирского вагона в пути следования Подготовка к СОР. Решение задач на расчет сопротивлений
Подготовка к СОР. Решение задач на расчет сопротивлений Магнит өрісінің. Дивергенция және Роторы
Магнит өрісінің. Дивергенция және Роторы Магнитное поле
Магнитное поле гидрав
гидрав Демонтаж приборов электрооборудования автомобиля
Демонтаж приборов электрооборудования автомобиля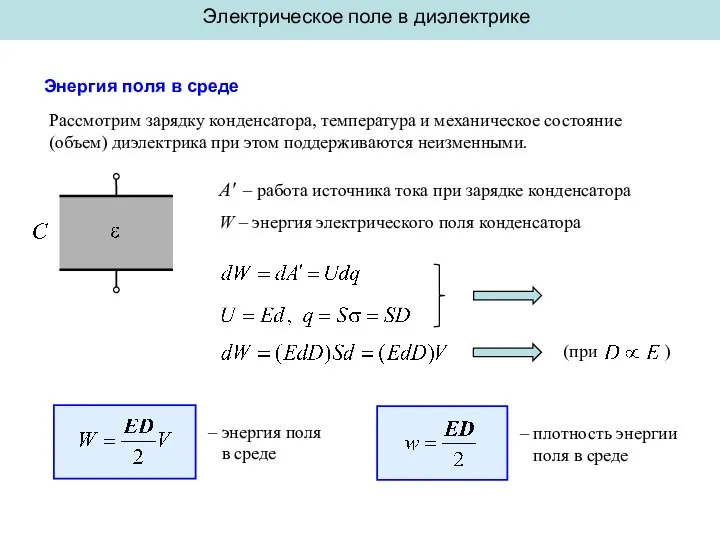 Энергия поля в среде
Энергия поля в среде Волновые свойства света
Волновые свойства света Критерии прочности при изгибе. Распространение критериев прочности на случай циклического нагружения
Критерии прочности при изгибе. Распространение критериев прочности на случай циклического нагружения