Содержание
- 2. 3.1.11-16, 20-21 Предшествующее ДЗ:
- 3. Вероятность того, что вектор скорости молекулы «попадает в кубик» dxdydz вблизи v вычисляется по правилу умножения
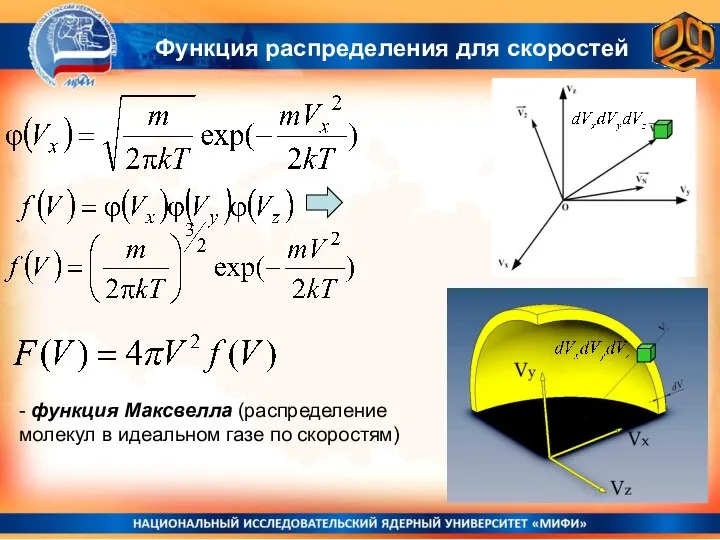
- 4. Функция распределения для скоростей ВАЖНО: Функция распределения по скоростям молекул зависит только от модуля (квадрата модуля)
- 5. Функция распределения для скоростей Условие нормировки: А = (a/2π)½ - интеграл Пуассона φ(vx2) = Аexp(-avx2/2); где
- 6. Функция распределения для скоростей Найдем среднее значение квадрата скорости молекулы: Этот интеграл тоже сводится к интегралу
- 7. Функция распределения для скоростей Из закона равнораспределения энергии по степеням свободы следует: φ(vx) = (2π )-½
- 8. Функция распределения для скоростей - функция Максвелла (распределение молекул в идеальном газе по скоростям)
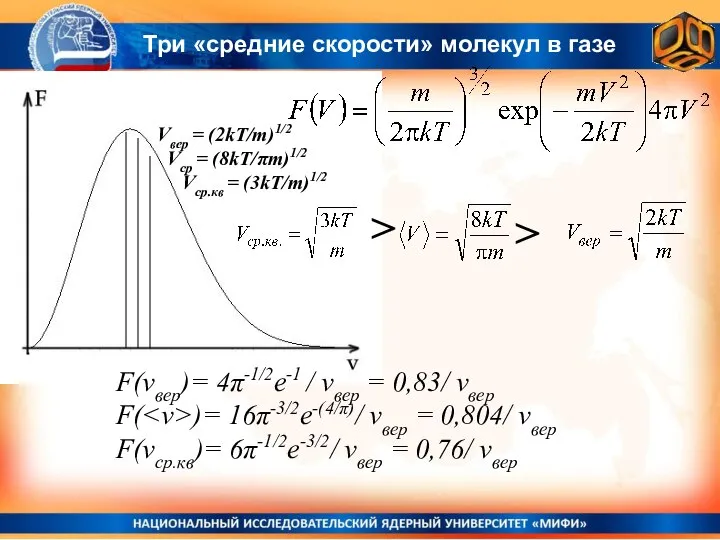
- 9. Функция Максвелла для разных температур и масс молекул Площадь под кривой ВСЕГДА равна единице
- 10. Vвер = (2kT/m)1/2 Vср = (8kT/πm)1/2 Vср.кв = (3kT/m)1/2 > F(vвер)= 4π-1/2е-1 / vвер = 0,83/
- 11. ПРИМЕР: Пример: Смесь азота и кислорода находится при температуре T = 300 K. Найти средние скорости
- 12. ПРИМЕР: Пример: Какая примерно доля молекул газа имеет скорости в интервале между cамой вероятной и средней
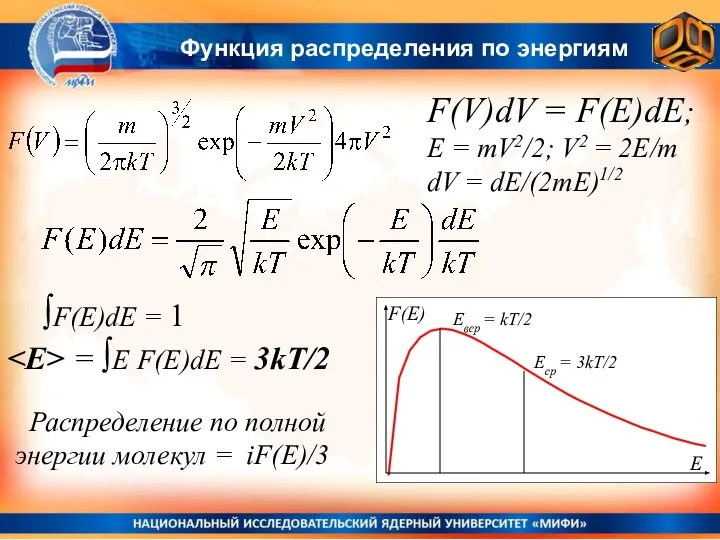
- 13. Функция распределения по энергиям F(V)dV = F(E)dE; E = mV2/2; V2 = 2E/m dV = dE/(2mE)1/2
- 14. Функция распределения для энергий Если учесть, что в гравитационном поле Земли молекулы обладают еще и потенциальной
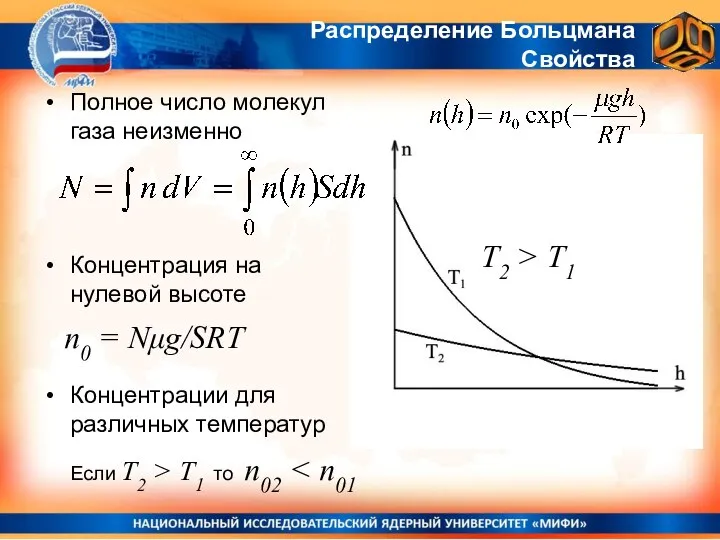
- 15. Полное число молекул газа неизменно Концентрация на нулевой высоте Концентрации для различных температур Распределение Больцмана Свойства
- 16. Распределение Больцмана Зависимость концентрации молекул в атмосфере от высоты - распределение Больцмана. p0 = n0kT =
- 17. Распределение Больцмана Зависимость концентрации молекул в атмосфере от высоты - распределение Больцмана. p0 = n0kT =
- 18. Парциальные давления в атмосфере p02(h)/pN2(h) = (21/78)exp((μN -μO)gh/RT) На высоте ~10км p02(h)/pN2(h) = 18/82 ПРИМЕР: p(h)
- 19. Парциальные давления в атмосфере ПРИМЕР: пылинки массой 10-18 г взвешены в воздухе при температуре 300 К.
- 20. Распределение Больцмана для дискретного энергетического спектра. Число частиц с энергией Е В случае дискретного спектра энергий,
- 21. Пример. Система состоящая из N молекул имеет температуру Т. Энергия частиц может принимать два значения Е1=kT
- 22. Определить поток частиц , вытекающих из поддерживаемого при постоянной температуре T сосуда через небольшое отверстие радиуса
- 23. 3.1.11-16, 20-21 Новое ДЗ: 3.2.1, 3--16, 20-21
- 25. Скачать презентацию


















 Движение молекул
Движение молекул Защита космонавтов, совершающих дальние космические перелёты, от радиации
Защита космонавтов, совершающих дальние космические перелёты, от радиации Вещества в электрическом поле
Вещества в электрическом поле Плоские дефекты, двумерные наноструктуры, большеугловые границы. Поликристаллическая структура
Плоские дефекты, двумерные наноструктуры, большеугловые границы. Поликристаллическая структура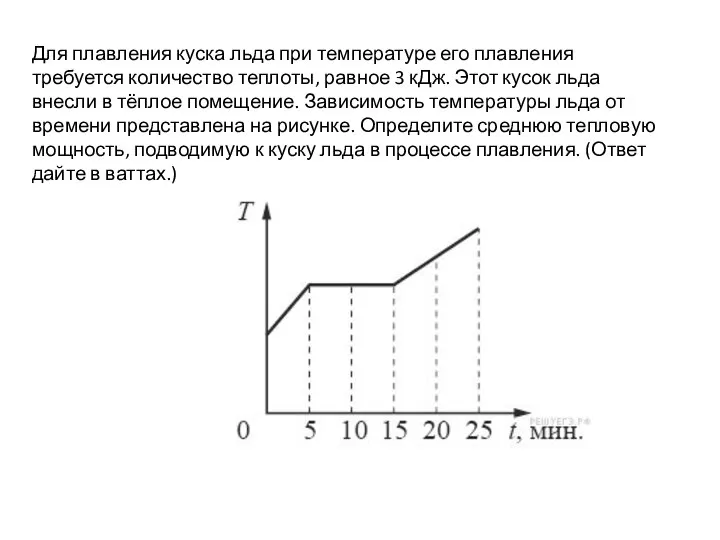 Определение тепловой мощности. ВПР, 9 класс
Определение тепловой мощности. ВПР, 9 класс РавноускДвиж.СвободПадение
РавноускДвиж.СвободПадение Последовательное соединение проводников. 8 класс
Последовательное соединение проводников. 8 класс Игровая технология в преподавании физики
Игровая технология в преподавании физики Экспериментальное исследование и расчет динамических режимов работы бытовой холодильной машины
Экспериментальное исследование и расчет динамических режимов работы бытовой холодильной машины Распределения вероятности. Нормальное распределение. Вероятностная энтропия. Лекция 07(10)
Распределения вероятности. Нормальное распределение. Вероятностная энтропия. Лекция 07(10) Электрические цепи переменного тока
Электрические цепи переменного тока Физика Лекция 2
Физика Лекция 2 Работа, мощность, энергия. Обобщающий урок
Работа, мощность, энергия. Обобщающий урок Схемный анализ ОЭП
Схемный анализ ОЭП Метаматериалы
Метаматериалы Использование данных лазерного сканирования для мониторинга состояния ВПП аэропорта
Использование данных лазерного сканирования для мониторинга состояния ВПП аэропорта Магнитная индукция
Магнитная индукция Физика атомного ядра. Радиоактивность. Приборы для регистрации элементарных частиц
Физика атомного ядра. Радиоактивность. Приборы для регистрации элементарных частиц Закон Бойля-Мариотта
Закон Бойля-Мариотта Закон Ома для участка цепи
Закон Ома для участка цепи Линзы. Построения в линзах. 11 класс
Линзы. Построения в линзах. 11 класс Физическая химия
Физическая химия График гармонического колебания
График гармонического колебания Плоский механизм. Задача 4
Плоский механизм. Задача 4 Излучение и все о нем
Излучение и все о нем Рация - переносное приёмо-передающее устройство
Рация - переносное приёмо-передающее устройство Электрические цели. Работа тока
Электрические цели. Работа тока Количество теплоты
Количество теплоты