Содержание
- 2. Цель: исследовать явление термодиффузии во флюиде Леннарда-Джонса методом молекулярной динамики, получить зависимости фактора термодиффузии бинарной системы
- 3. Метод молекулярной динамики (метод МД) — это метод, основанный на том, что временнáя эволюция системы взаимодействующих
- 4. Данный метод позволяет моделировать детальную микроскопическую картину внутренней подвижности систем, состоящих из молекул. В его основе
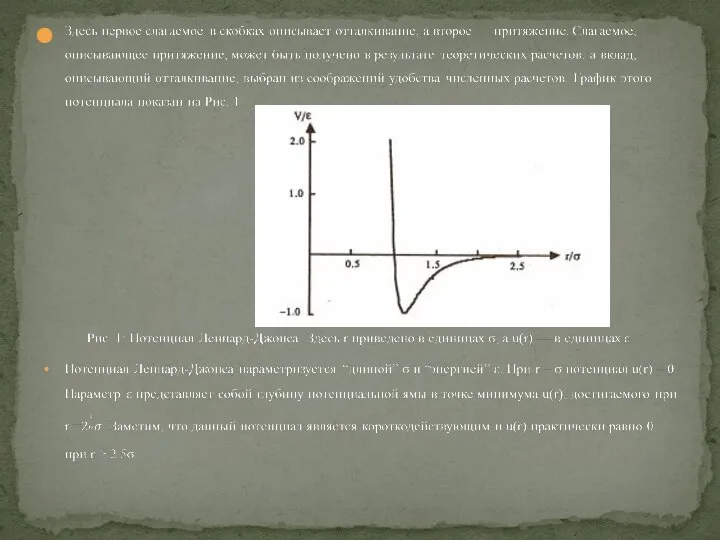
- 5. Потенциал межмолекулярного взаимодействия
- 7. ММД основывается на численном решении систем дифференциальных уравнений движения вида: Для численного решения необходимо представить уравнение
- 8. Как можно увидеть из (3), основная вычислительная нагрузка приходится на расчет результирующей силы парного взаимодействия, следовательно
- 9. При проведении МД-расчетов для свободных нанокластеров при умеренной температуре не возникает необходимости в ограничении моделируемого пространства.
- 10. Граничные условия определяют термодинамическое окружение системы, поэтому они составляют существенную часть молекулярно-динамических моделей. Наиболее важным методом
- 11. В реальных экспериментах температура системы поддерживается за счёт энергообмена с внешней средой. Детальный учёт взаимодействия молекулы
- 12. Этот метод имеет то преимущество, что интенсивность теплообмена может изменяться и адаптироваться под конкретные цели: для
- 13. Макроскопические свойства системы рассчитываются только после достижения системой стабильных статистических характеристик. Ниже приведены способы вычисления некоторых
- 14. Температура может быть вычислена через кинетическую энергию. Так как каждая вращательная степень свободы вносит вклад размера
- 15. В изолированной системе, содержащей смесь n компонентов с неоднородным первоначальным распределением концентраций, возникает процесс переноса массы
- 16. В бинарной смеси при постоянном давлении в отсутствии внешних сил полный диффузионный поток вещества равен ji
- 18. Скачать презентацию
Слайд 2Цель: исследовать явление термодиффузии во флюиде Леннарда-Джонса методом молекулярной динамики, получить зависимости
Цель: исследовать явление термодиффузии во флюиде Леннарда-Джонса методом молекулярной динамики, получить зависимости

Чтобы это осуществить, нужно решить несколько задач:
1. Исследовать необходимую литературу о методе молекулярной динамики и алгоритмах, которые он использует
2. Исследовать литературу о явлении термодиффузии, методах расчета и экспериментального определения фактора и коэффициента термодиффузии
3. Разработать алгоритмы, позволяющие вычислить фактор термодиффузии бинарной сиситемы частиц в рамках метода молекулярной динамики
4. Проверить работоспособность программы молекулярной динамики на примере системы, находящейся в термодинамическом равновесии.
5. Провести вычислительный эксперимент с помощью программы молекулярной динамики по исследованию явления термодиффузии многочастичной системы, проанализировать полученные результаты.
Цели и задачи проекта
Слайд 3Метод молекулярной динамики (метод МД) — это метод, основанный на том, что
Метод молекулярной динамики (метод МД) — это метод, основанный на том, что

О методе молекулярной динамики
Слайд 4Данный метод позволяет моделировать детальную микроскопическую картину внутренней подвижности систем, состоящих из
Данный метод позволяет моделировать детальную микроскопическую картину внутренней подвижности систем, состоящих из

Данный метод можно применять, если длина волны Де Бройля атома (частицы) много меньше, чем межатомное расстояние. Также классическая молекулярная динамика не применима для моделирования систем состоящих из легких атомов, таких как гелий или атомарный водород. При низких температурах квантовые эффекты становятся определяющими и для рассмотрения таких систем необходимо использовать квантовохимические методы. Необходимо, чтобы времена, на которых рассматривается поведение системы, были больше чем время релаксации исследуемых физических величин
Применение метода МД и его ограничения
Слайд 5Потенциал межмолекулярного взаимодействия
Потенциал межмолекулярного взаимодействия

Слайд 7ММД основывается на численном решении систем дифференциальных уравнений движения вида:
Для численного решения
ММД основывается на численном решении систем дифференциальных уравнений движения вида:
Для численного решения

Численное решение уравнений движения
Слайд 8Как можно увидеть из (3), основная вычислительная нагрузка приходится на расчет результирующей
Как можно увидеть из (3), основная вычислительная нагрузка приходится на расчет результирующей

Далее, разлагая (5) и (6) в ряд Тейлора, можно получить выражения для различных схем интегрирования, от простейших методов Эйлера и Эйлера-Кромера до алгоритма Верле и Бимана. Последние два алгоритма наиболее востребованы из за своей высокой точности.
Алгоритм Бимана обладает наибольшим порядком точности. Он может применяться в случаях, когда весомое значение имеют фазовые траектории отдельных частиц системы. Главным недостатком данной схемы является то, что она не обладает самостартуемостью, т.к. для вычисления состояния в последующий момент времени используются значения в предыдущий момент. Для решения данной проблемы первый шаг интегрирования обычно производят менее точными алгоритмами, например Эйлера-Кромера
Метод Верле, является компромиссом между точностью процедуры и скоростью её реализации. Этот метод является, пожалуй, одним из самых точных в классе методов интегрирования первого порядка
Слайд 9При проведении МД-расчетов для свободных нанокластеров при умеренной температуре не возникает необходимости
При проведении МД-расчетов для свободных нанокластеров при умеренной температуре не возникает необходимости

Простейшим вариантом такой границы является ящик с отражающими стенками. Всякий раз, когда частица в процессе моделирования достигает внутренней поверхности ящика, ее перпендикулярная компонента скорости меняет знак. При таком граничном условии сохраняются энергия и объем системы, а также остается постоянным число частиц. Иными словами, имеется в виду изолированная система. В другом варианте отражение может зависеть от импульса частицы. Если перпендикулярная компонента скорости частицы превышает некоторое значение, она может покинуть ящик и, таким образом, исключается из дальнейшего рассмотрения. Есть ещё более оптимальный вариант: ящик заменяется сферическим потенциальным барьером, который частица может преодолеть, только обладая достаточной кинетической энергией.
Граничные условия
Слайд 10Граничные условия определяют термодинамическое окружение системы, поэтому они составляют существенную часть молекулярно-динамических
Граничные условия определяют термодинамическое окружение системы, поэтому они составляют существенную часть молекулярно-динамических

Периодические граничные условия позволяют рассматривать сравнительно небольшой «кубик» пространства, в котором расположена изучаемая молекула. Молекулы внутри кубика со временем совершают конформационные движения и перемещаются в пространстве, причем могут пересечь границы кубика. Суть метода заключается в том, что пространство разбивается на одинаковые кубики и предполагается, что их содержимое одинаково, а границы соприкасаются. При пересечении молекулой границы одного кубика она оказывается в другом, но при этом в первый кубик с противоположной стороны попадает такая же молекула. При таком подходе достаточно смоделировать динамику лишь одного такого кубика. Естественно, его размер должен быть достаточно большим, чтобы исключить возможность краевых эффектов.
Слайд 11В реальных экспериментах температура системы поддерживается за счёт энергообмена с внешней средой.
В реальных экспериментах температура системы поддерживается за счёт энергообмена с внешней средой.

Алгоритм (термостат) Берендсена корректирует производную температуры по времени согласно уравнению
т.е. отклонения температуры (T-T0) экспоненциально убывают c временной постоянной равной τT . Поскольку температура определяется кинетической энергией, которая пропорциональна квадрату скорости частиц, то корректируется не сама температура, а скорость частиц. Для этого после определения скоростей частиц их значения умножаются на фактор λ :
Термостат Берендсена
Слайд 12Этот метод имеет то преимущество, что интенсивность теплообмена может изменяться и адаптироваться
Этот метод имеет то преимущество, что интенсивность теплообмена может изменяться и адаптироваться

Слайд 13Макроскопические свойства системы рассчитываются только после достижения системой стабильных статистических характеристик. Ниже
Макроскопические свойства системы рассчитываются только после достижения системой стабильных статистических характеристик. Ниже

Энергия. Потенциальная энергия системы ???? и кинетическая энергия системы ???? вычисляются как суммы, соответственно, потенциальных и кинетических энергий всех частиц:
где ? — число атомов в системе. В случае многоатомных жестких молекул к ???? добавляется кинетическая энергия вращательного движения
Полная энергия системы ? представляет собой сумму потенциальной и кинетической энергий
Расчет макроскопических свойств
Слайд 14Температура может быть вычислена через кинетическую энергию. Так как каждая вращательная степень
Температура может быть вычислена через кинетическую энергию. Так как каждая вращательная степень

где ?? — константа Больцмана, ? — число степеней свободы. При трехмерном моделировании простых веществ, атомы которых взаимодействуют при помощи потенциала Леннард—Джонса, ? = 3.
Давление может быть вычислено при помощи уравнения состояния, если оно имеется для рассматриваемой системы, или при помощи вириальной теоремы по следующей формуле
где ? — объем области, ⟨. . .⟩ — обозначает осреднение по времени.
Плотность. Локальная плотность может быть вычислена при помощи разбиения области на ячейки и определения распределения частиц по ячейкам. Тогда локальная плотность в некоторой ячейке объемом ? , содержащей ? частиц массой ?, определяется по следующей формуле
Слайд 15В изолированной системе, содержащей смесь n компонентов с неоднородным первоначальным распределением концентраций,
В изолированной системе, содержащей смесь n компонентов с неоднородным первоначальным распределением концентраций,

Виды молекулярной диффузии (по причине возникновения):
1. концентрационная – за счёт разности концентраций;
2. бародиффузия – за счёт разности парциальных давлений;
3. термодиффузия – за счёт разности температур (температурный градиент).
Термодиффузия (термическая, или тепловая, диффузия) - перенос компонент газовых смесей или растворов под влиянием градиента температуры. Если разность температур поддерживается постоянной, то вследствие термодиффузии в объёме смеси возникает градиент концентрации, что вызывает также и обычную диффузию. В стационарных условиях при отсутствии потока вещества термодиффузия уравновешивается с обычной диффузией. Термодиффузия в газах была теоретически предсказана английским учёным С. Чепменом и шведским учёным Д. Энскогом (1911—17) на основе кинетической теории газов и экспериментально обнаружена английскими учёными С. Чепменом и Ф. Дутсоном в 1917.
Термодиффузия
Слайд 16В бинарной смеси при постоянном давлении в отсутствии внешних сил полный диффузионный
В бинарной смеси при постоянном давлении в отсутствии внешних сил полный диффузионный

ji = – nD12 gradci – n (DT/T) grad Т,
где D12 — коэффициент диффузии, DT — коэффициент термодиффузии, n — число частиц смеси в единице объёма, ci = ni/n — концентрация частиц i-й компоненты (i = 1,2).
с и (с-1) – концентрации компонентов смеси двух газов соответственно
Это приближенное аналитическое выражение для фактора термодиффузии лишь для случая идеального газа. Величина αT идеального газа зависит от разности масс компонент и показателя степени n, отвечающего за отталкивание в выражении для потенциала взаимодействия
 Дистанционное пилотирование БЛА самолетного типа
Дистанционное пилотирование БЛА самолетного типа Применение механизма Кланна в робототехнике
Применение механизма Кланна в робототехнике Число электронных слоев в атоме
Число электронных слоев в атоме Методологические основы и структура научного познания. Лекция №1
Методологические основы и структура научного познания. Лекция №1 Сила упругости. Закон Гука. 7 класс
Сила упругости. Закон Гука. 7 класс Винайдення фотографий
Винайдення фотографий Замена прокладки ГБЦ на семействе автомобилей ВАЗ
Замена прокладки ГБЦ на семействе автомобилей ВАЗ Ядерный реактор
Ядерный реактор Презентация на тему Расчёт массы тела по его плотности
Презентация на тему Расчёт массы тела по его плотности  Переменный ток
Переменный ток Физика- это наука понимать природу. Архимедова сила
Физика- это наука понимать природу. Архимедова сила Обеспечение требуемой точности машины. Тема 4
Обеспечение требуемой точности машины. Тема 4 Теория электромагнитного поля
Теория электромагнитного поля Технические измерения
Технические измерения T-S диаграмма
T-S диаграмма Dīzeļlokomotīvju bremžu iekārtu shēmas
Dīzeļlokomotīvju bremžu iekārtu shēmas Внутренняя энергия
Внутренняя энергия Физические основы микроэлектроники. Радиоматериалы и радиокомпоненты
Физические основы микроэлектроники. Радиоматериалы и радиокомпоненты Исследовательская работа по физике Модель двигателя Стирлинга
Исследовательская работа по физике Модель двигателя Стирлинга Динамика. Законы Ньютона
Динамика. Законы Ньютона Кинематика
Кинематика Pезонанс прояви і застосування
Pезонанс прояви і застосування Движение твердой среды
Движение твердой среды Конденсаторы. Задачи на соответствия из 1 и 2 части ЕГЭ
Конденсаторы. Задачи на соответствия из 1 и 2 части ЕГЭ Презентация на тему Физика и познание мира
Презентация на тему Физика и познание мира  Тест. Механические колебания
Тест. Механические колебания Примеры теплопередач в природе, быту и технике
Примеры теплопередач в природе, быту и технике Законы Ньютона
Законы Ньютона