Технология компрессии изображений Smart Compression of Images

CONTENTS
Objectives
Smart Compression of Images Procedure
Example 1. Lossy Compression Mode
Third Step – the Core of General Algorithm
Segments Comparison
Example 2: Segments Comparison
Minimal Basic Subset of Segments Selection
Example 3: Minimal Basic Subset of Segments
Selection
Smart Compression of Colored Images
Main Features of Smart Compression
Experiment 1: Smart Compression and JPG Comparison
Experiment 2: probability of optimality for different segment sizes as a function of size of an image

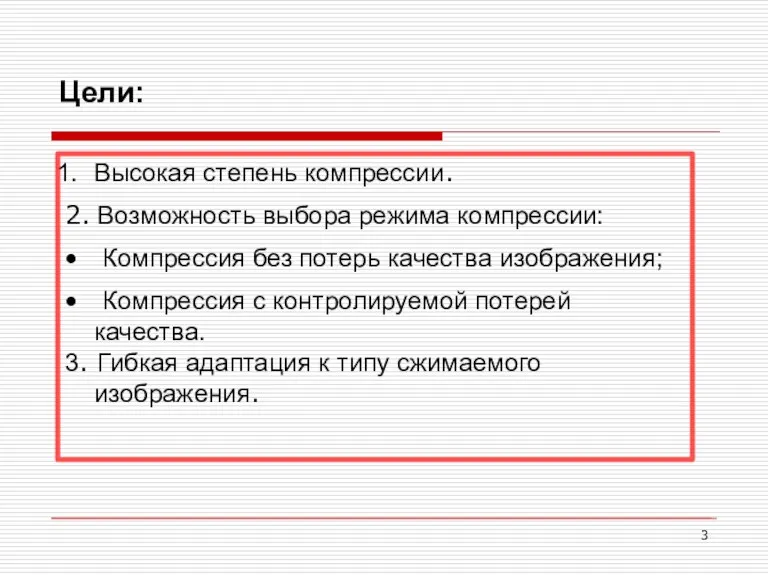
Цели:
Высокая степень компрессии.
2. Возможность выбора режима компрессии:
Компрессия без потерь качества изображения;
Компрессия с контролируемой потерей качества.
3. Гибкая адаптация к типу сжимаемого изображения.

Алгоритм «Smart Compression of Images»
Основной алгоритм компрессии вариабельными фрагментами
Выбор размеров квадратного фрагмента, на которые делится изображение, не анализировавшегося ранее. Если таковых нет – переход к шагу 7
Декомпозиция изображения на фрагменты.
Выделение минимального подмножества фрагментов, позволяющих восстановить исходное изображение с заданным уровнем искажений с помощью функций преобразования фрагментов.
Вычисление коэффициента компрессии “η”. Если он больше хранящегося в памяти, то переход к шагу 5, в противном случае – к шагу 6.
Прежнее значение коэффициента компрессии и соответствующий размер фрагмента забываются, а новые – запоминаются.
Выбранный на шаге 1 последней итерации фрагмент считаем анализировавшимся. Переход к шагу 1.
7. Конец алгоритма.

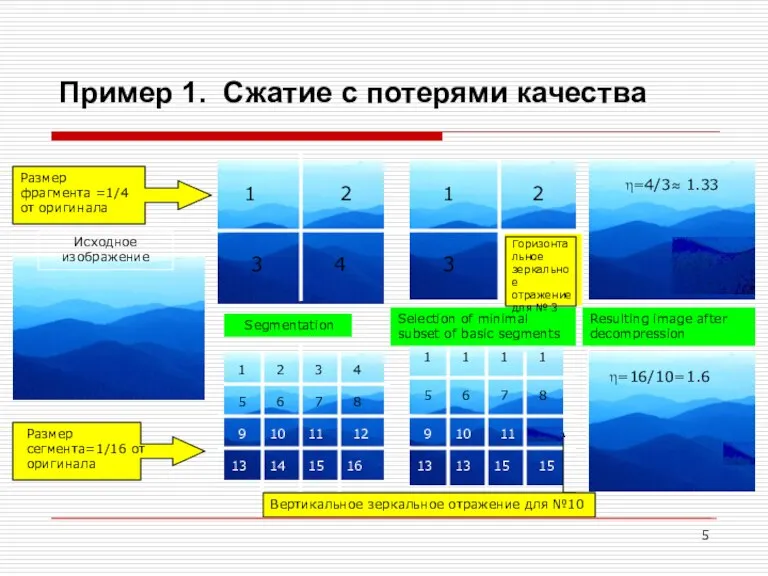
Пример 1. Сжатие с потерями качества
Размер фрагмента =1/4 от оригинала
Размер сегмента=1/16 от оригинала
Segmentation
Selection of minimal subset of basic segments
Resulting image after decompression
η=4/3≈ 1.33
η=16/10=1.6
1
2
3
4
Горизонтальное зеркальное отражение для № 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
1
1
13
15
Вертикальное зеркальное отражение для №10
1
5
6
7
8
9
10
11
13
15
1
2
3
Исходное изображение

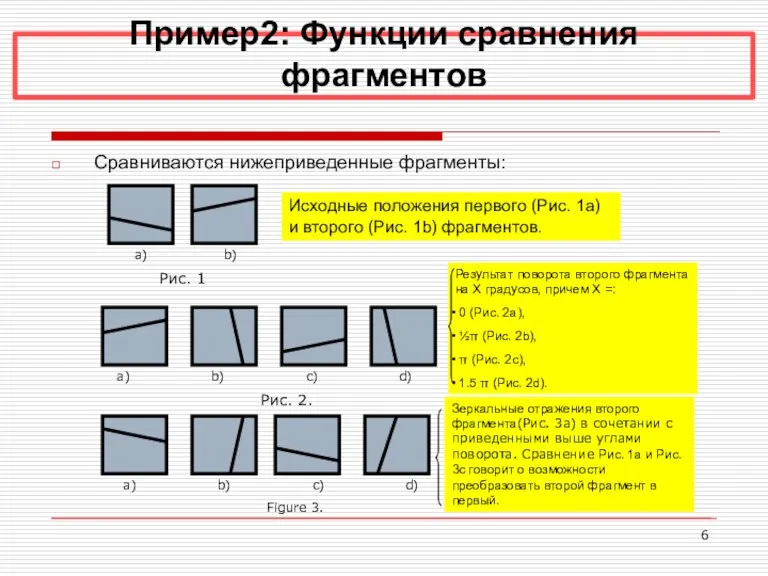
Пример2: Функции сравнения фрагментов
Сравниваются нижеприведенные фрагменты:
a) b)‏
Рис. 1
Исходные положения первого (Рис. 1a) и второго (Рис. 1b) фрагментов.
a) b) c) d)‏
Рис. 2.
Результат поворота второго фрагмента на Х градусов, причем Х =:
0 (Рис. 2a),
½π (Рис. 2b),
π (Рис. 2с),
1.5 π (Рис. 2d).
a) b) c) d)‏
Figure 3.
Зеркальные отражения второго фрагмента(Рис. 3a) в сочетании с приведенными выше углами поворота. Сравнение Рис. 1a и Рис. 3c говорит о возможности преобразовать второй фрагмент в первый.

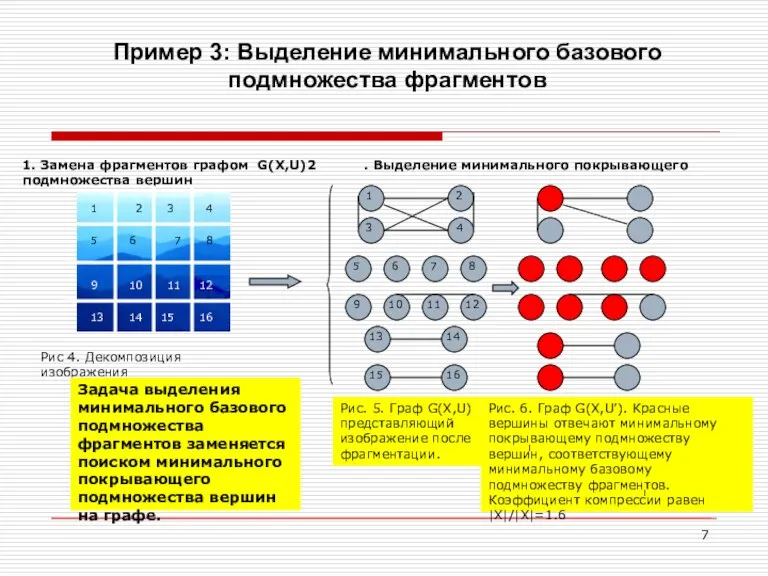
Пример 3: Выделение минимального базового подмножества фрагментов
1. Замена фрагментов графом G(X,U)‏ 2. Выделение минимального покрывающего подмножества вершин
1
2
3
4
5
6
7
8
9
10
11
12
15
14
13
16
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Рис 4. Декомпозиция изображения
Рис. 5. Граф G(X,U) представляющий изображение после фрагментации.
Рис. 6. Граф G(X,U’). Красные вершины отвечают минимальному покрывающему подмножеству вершин, соответствующему минимальному базовому подмножеству фрагментов. Коэффициент компрессии равен |X|/|X|=1.6
Задача выделения минимального базового подмножества фрагментов заменяется поиском минимального покрывающего подмножества вершин на графе.

Компрессия цветных изображений
Smart Compression использует разложение на три цвета, каждый из которых имеет градации яркости 0 – 256 each (Рис. 7).
Рис. 7.
Одним из способов использования вышеописанной технологии является компрессия каждой монохромной картинки отдельно..

Аналитические закономерности компрессии статичных изображений вариабельными фрагментами
Теорема 1. Оптимальное число квадратных фрагментов N, разбиение на которое позволяет получить максимальный коэффициент компрессии, в первом приближении равно:
где: Q – размер оригинального изображения;
D – объем информации о каждом фрагменте, хранимый в
памяти и достаточный для его восстановления;
k - коэффициент пропорциональности.

Минимизация времени компрессии в однородных вычислительных средах
Теорема 2.
Оптимальное число используемых однородных процессоров, минимизирующее время сравнения фрагментов изображения, равно:
Оптимальное число используемых однородных процессоров, минимизирующее время выделения минимального базового подмножества фрагментов изображения, равно:
где: Р – число процессоров однородной
вычислительной среды; k - коэффициент
пропорциональности; g – пропускная способность
канала связи (Кб/сек)
Теорема 3.