Содержание
- 2. План решения задач по динамике 1. Сделать рисунок, на котором обозначить направление координатных осей, ускорения и
- 3. Движение по наклонной плоскости ВАЖНО ПОМНИТЬ mg N F Fтр. Для тела, расположенного на наклонной плоскости
- 4. а β m1g m2g N1 N2 T T У У Х Х а а С каким
- 5. № 1: Два тела, связанные невесомой нерастяжимой нитью (см. рис.) тянут с силой 15 Н вправо
- 7. № 2. К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок без трения в оси,
- 9. № 3. Брусок массой 2 кг скользит по горизонтальной поверхности под действием груза массой 0,5 кг,
- 11. № 4. Груз массой 5 кг, связанный нерастяжимой нитью, перекинутой через неподвижный блок, с другим грузом
- 13. а У Х FN1 N2 m1g m2g T T Fтр. Fтр1.1 Человек массой m1 , упираясь
- 14. Шары массами m1 ,m2 ,m3 подвешены к потолку с помощью двух невесомых пружин и легкой нити.
- 16. Скачать презентацию
Слайд 2План решения задач по динамике
1. Сделать рисунок, на котором обозначить направление
План решения задач по динамике
1. Сделать рисунок, на котором обозначить направление

осей, ускорения и всех сил, приложенных к телу .
2. Для каждого тела записать в векторном виде уравнение второго закона Ньютона, перечислив в его правой части в любом порядке все силы, приложенные к телу
3. Записать полученные в п. 2 уравнения в проекции
на оси координат.
5. Найти численное значение неизвестной величины,
если этого требует условие задачи.
4. Из полученного уравнения (системы уравнений) выразить неизвестную величину.
Слайд 3Движение по наклонной плоскости
ВАЖНО ПОМНИТЬ
mg
N
F
Fтр.
Для тела, расположенного
Движение по наклонной плоскости
ВАЖНО ПОМНИТЬ
mg
N
F
Fтр.
Для тела, расположенного
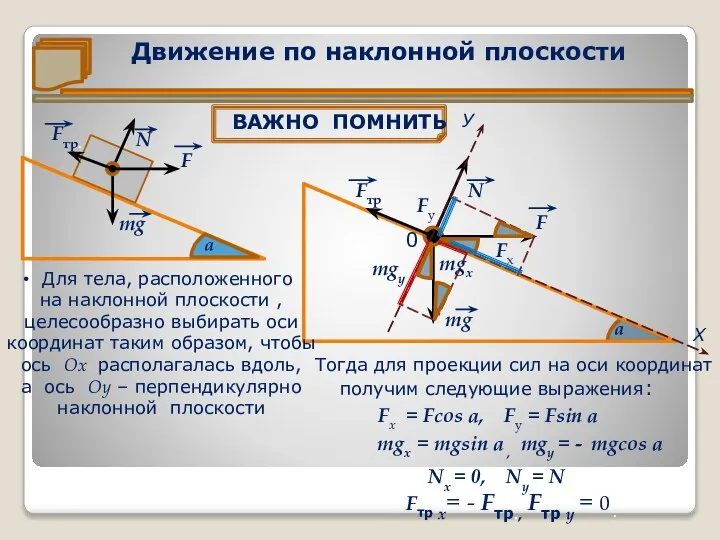
на наклонной плоскости ,
целесообразно выбирать оси
координат таким образом, чтобы
ось Ох располагалась вдоль,
а ось Оу – перпендикулярно
наклонной плоскости
а
Тогда для проекции сил на оси координат
получим следующие выражения:
Fх. = Fcos а, Fу = Fsin а
mgх. = mgsin а , mgу = - mgcos а
Nx = 0,
Ny = N
Fтр x= - Fтр., Fтр у = 0 .
Слайд 4а
β
m1g
m2g
N1
N2
T
T
У
У
Х
Х
а
а
С каким ускорением будут двигаться грузы массами 2
а
β
m1g
m2g
N1
N2
T
T
У
У
Х
Х
а
а
С каким ускорением будут двигаться грузы массами 2
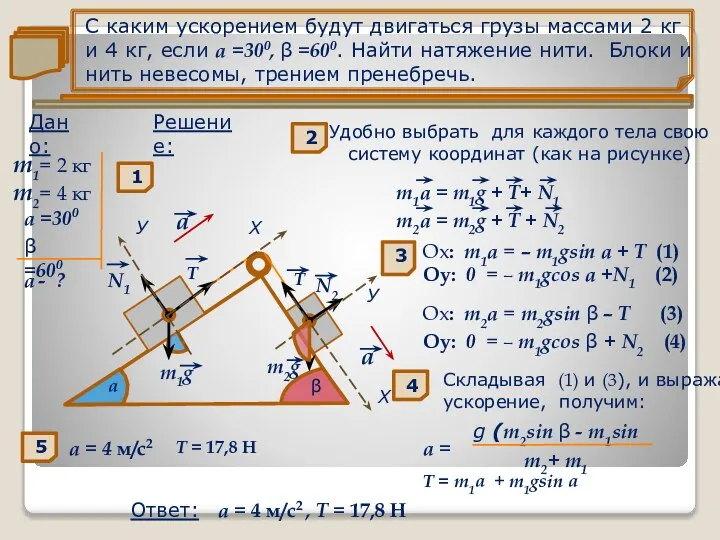
m1= 2 кг
m2= 4 кг
Дано:
а =300
β =600
а - ?
Решение:
1
2
Удобно выбрать для каждого тела свою
систему координат (как на рисунке)
m1a = m1g + Т+ N1
m2a = m2g + Т + N2
3
Оx: m1a = – m1gsin а + Т (1)
Оy: 0 = – m1gcos а +N1 (2)
Оx: m2a = m2gsin β – Т (3)
Оy: 0 = – m1gcos β + N2 (4)
4
Складывая (1) и (3), и выражая
ускорение, получим:
g (m2sin β - m1sin
a =
m2+ m1
Т = 17,8 H
T = m1a + m1gsin а
5
a = 4 м/с2
Ответ: а = 4 м/с2 , T = 17,8 H
Слайд 5№ 1: Два тела, связанные невесомой нерастяжимой нитью (см. рис.) тянут с
№ 1: Два тела, связанные невесомой нерастяжимой нитью (см. рис.) тянут с
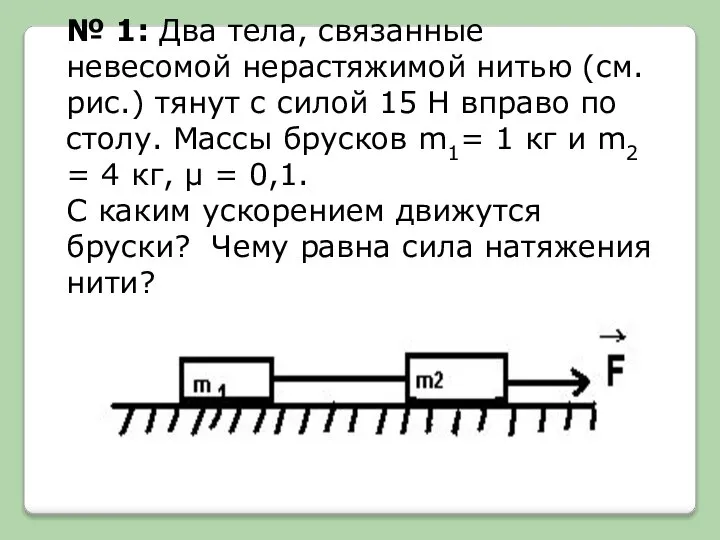
С каким ускорением движутся бруски? Чему равна сила натяжения нити?
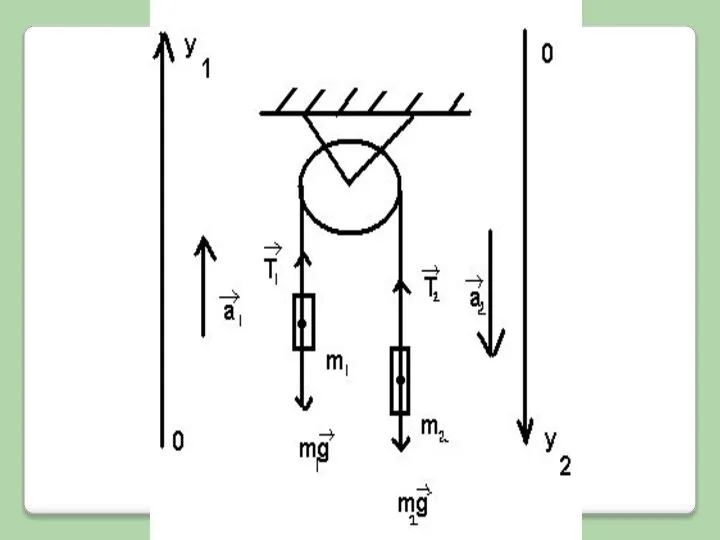
Слайд 7№ 2. К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок
№ 2. К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок

№ 2. К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок без трения в оси, подвешены грузы с массами m1= 1кг и m2= 2 кг. Каково ускорение, с которым движется второй груз?
Слайд 9
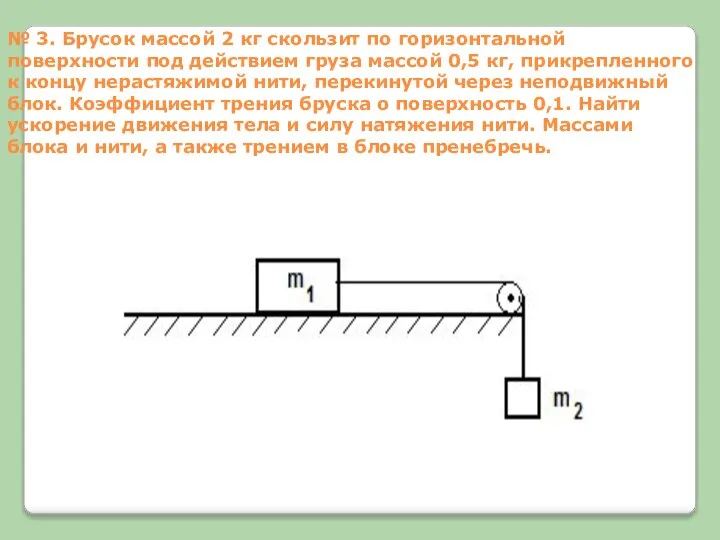
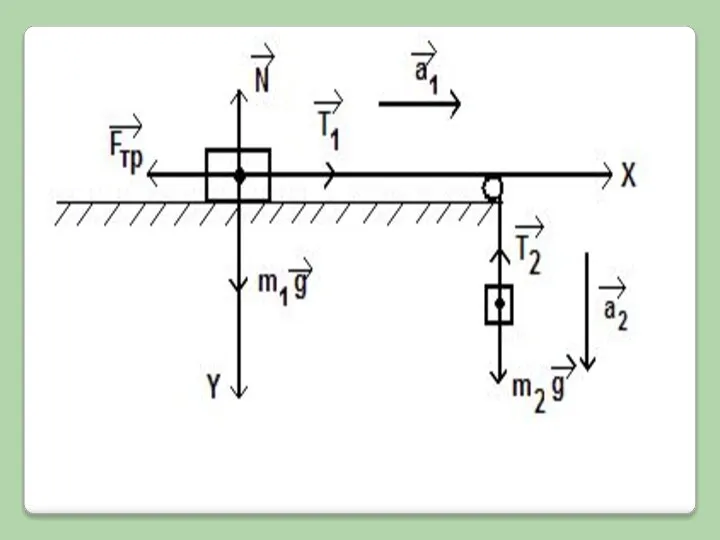
№ 3. Брусок массой 2 кг скользит по горизонтальной поверхности под действием
№ 3. Брусок массой 2 кг скользит по горизонтальной поверхности под действием
Слайд 11
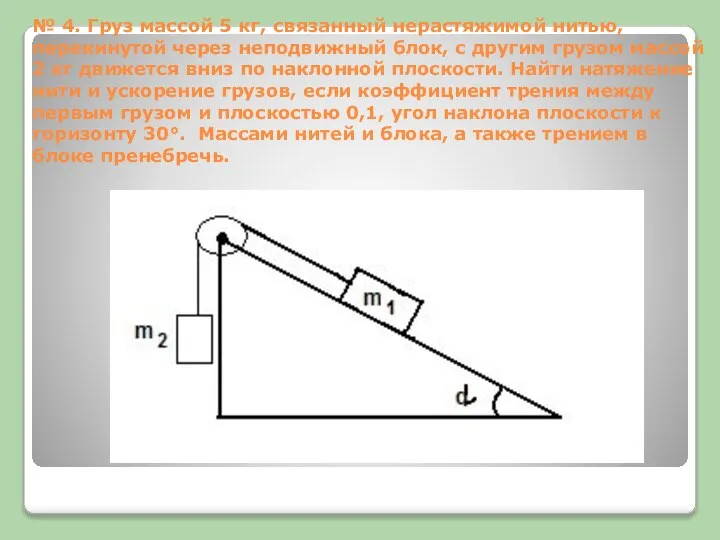
№ 4. Груз массой 5 кг, связанный нерастяжимой нитью, перекинутой через неподвижный
№ 4. Груз массой 5 кг, связанный нерастяжимой нитью, перекинутой через неподвижный
Слайд 13а
У
Х
FN1
N2
m1g
m2g
T
T
Fтр.
Fтр1.1
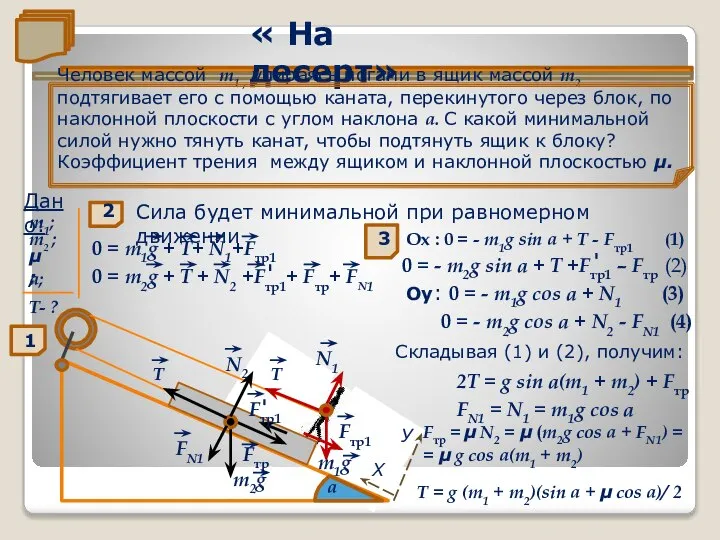
Человек массой m1 , упираясь ногами в ящик
а
У
Х
FN1
N2
m1g
m2g
T
T
Fтр.
Fтр1.1
Человек массой m1 , упираясь ногами в ящик
« На десерт»
1
Дано:
m1;
m2 ;
μ;
а;
T- ?
Сила будет минимальной при равномерном движении
2
0 = m1g + Т+ N1+Fтр1
0 = m2g + Т + N2 +Fтр1+ Fтр+ FN1
3
Ох : 0 = - m1g sin а + Т - Fтр1 (1)
0 = - m2g sin а + Т +Fтр1 – Fтр (2)
Оу: 0 = - m1g cos а + N1 (3)
0 = - m2g cos а + N2 - FN1 (4)
N1
FN1 = N1 = m1g cos а
Складывая (1) и (2), получим:
2Т = g sin а(m1 + m2) + Fтр
Fтр = μ N2 = μ (m2g cos а + FN1) =
= μ g cos а(m1 + m2)
Т = g (m1 + m2)(sin а + μ cos а)/ 2
Слайд 14Шары массами m1 ,m2 ,m3 подвешены к потолку с помощью двух невесомых
Шары массами m1 ,m2 ,m3 подвешены к потолку с помощью двух невесомых

m1g
T
T
m2g
Fупр1.
Fупр2.
Fупр2.
m3g
m1;
m2 ;
m3 ;
а-?
T-?
Дано:
Решение:
У
0
а
1. Для ясности можно провести «мысленный
эксперимент» – представить, что в середине
нити находится динамометр. Получается ,
что к нему прикрепили грузы массами m2 и m3. Естественно, его показания будут равны:
Т = g (m2 + m3 )
2. В момент пережигания нити на верхний шар
действуют только две силы : Fупр1. и m1g , которые
и сообщают шару ускорение.
m1a = m1g +Fупр1
Fупр1 = g (m1 + m 2 + m3 ) ( см. п.1 )
a = g (m2 + m3 ) / m1
Окончательно после преобразований получим:


 Распространение теплоты в однородных материалах. Теплопроводность однослойной и многослойной плоских стенок. (Занятие 9)
Распространение теплоты в однородных материалах. Теплопроводность однослойной и многослойной плоских стенок. (Занятие 9) Кең ауқымды вибратор
Кең ауқымды вибратор Импульс тела. Задачи
Импульс тела. Задачи Магнитное поле тока
Магнитное поле тока Устройство нанопинцет
Устройство нанопинцет Система питания инжекторного двигателя. Система распределенного впрыска LН-Getronic
Система питания инжекторного двигателя. Система распределенного впрыска LН-Getronic Тела вращения
Тела вращения Источники звука. Звуковые волны
Источники звука. Звуковые волны Обеспечение требуемой точности машины. Тема 4
Обеспечение требуемой точности машины. Тема 4 Молниезащита зданий и сооружений
Молниезащита зданий и сооружений Получение радиоактивных изотопов и их применение
Получение радиоактивных изотопов и их применение Равновесие системы сходящихся сил. Система параллельных сил и пар
Равновесие системы сходящихся сил. Система параллельных сил и пар Силы в природе
Силы в природе Электромагнитные взаимодействия ядер
Электромагнитные взаимодействия ядер Электростатическое взаимодействие. Движение электрических зарядов. Электромагнитное поле
Электростатическое взаимодействие. Движение электрических зарядов. Электромагнитное поле Окружающие нас тела называются физическими телами. Строение вещества. Молекула
Окружающие нас тела называются физическими телами. Строение вещества. Молекула Профильное обучение физике в процессе модернизации школьного образования
Профильное обучение физике в процессе модернизации школьного образования Электрический ток в металлах
Электрический ток в металлах Физические свойства наноматериалов
Физические свойства наноматериалов Координационная химия и солнечная энергетика
Координационная химия и солнечная энергетика Теоретическая механика. Модуль 1. Раздел 3 – динамика точки
Теоретическая механика. Модуль 1. Раздел 3 – динамика точки Расчёт электромагнитного поля (ЭМП)
Расчёт электромагнитного поля (ЭМП) Ученые-физики
Ученые-физики Lek_01_Elek_22
Lek_01_Elek_22 Магнитное поле
Магнитное поле Проверочные вопросы по теме Этапы работы над исследовательским проектом
Проверочные вопросы по теме Этапы работы над исследовательским проектом Конкурс презентаций Если б Гарри Поттером был я
Конкурс презентаций Если б Гарри Поттером был я Типы соединений потребителей тока
Типы соединений потребителей тока