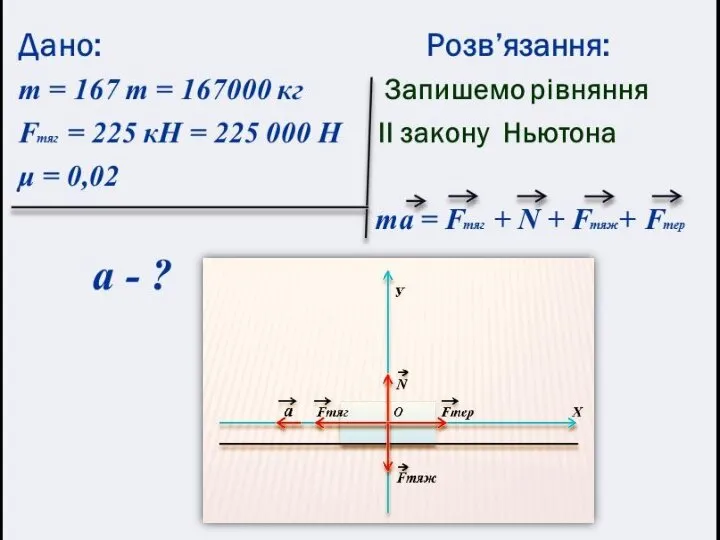
Слайд 2Визначте прискорення реактивного лайнера під час зльоту, якщо його маса 167 т,

сила тяги двигунів 225 кН, а коефіцієнт тертя коліс шасі об злітну смугу 0,02.
Слайд 4 F = Fтяг + N + Fтяж+ Fтер
Запишемо рівняння руху в

проекціях на вісь ОХ: - та = - Fтяг + Fтер
Запишемо рівняння руху в проекціях на вісь ОУ: 0 = N - Fтяж
Розв'яжемо систему з двох рівнянь:
- та = - Fтяг + Fтер
0 = N - Fтяж
Слайд 6На кінцях нитки, яка перекинута через нерухомий блок, підвішено гирі масою 11г

і 13г. Коли гирі відпустили, система почала рухатись з прискоренням 81,8 см/с². Визначте за цими даними прискорення вільного падіння.
Дано: Розв’язання:
m1 = 11г = 0,011кг Виконаємо рисунок
m2 = 13г = 0,013кг та покажемо всі сили,
а = 81,8 см/с² = 0,818м/с² які діють у системі:
g - ?
Слайд 7Запишемо рівняння руху у векторній формі для першого тіла:
m1 ·a= Fтяж,1
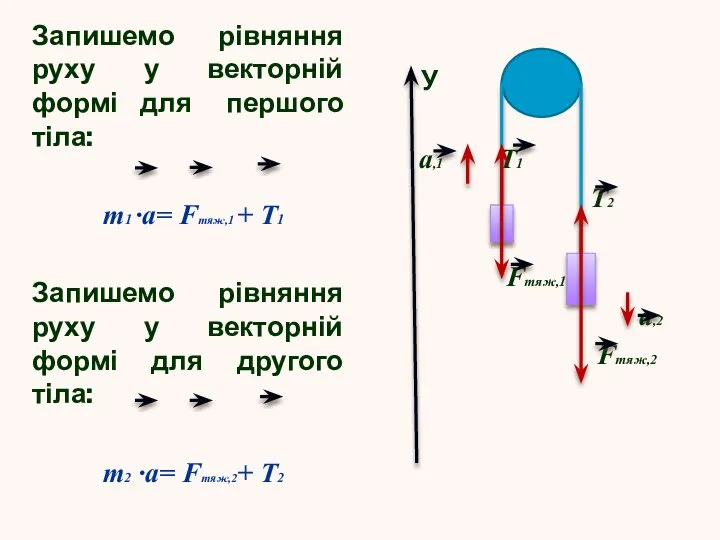
+ Т1
Запишемо рівняння руху у векторній формі для другого тіла:
m2 ·a= Fтяж,2+ Т2
У
а,1 Т1
Т2
Fтяж,1
а,2
Fтяж,2
Слайд 8Запишемо рівняння руху у проекції на вісь ОУ для першого тіла:
m1
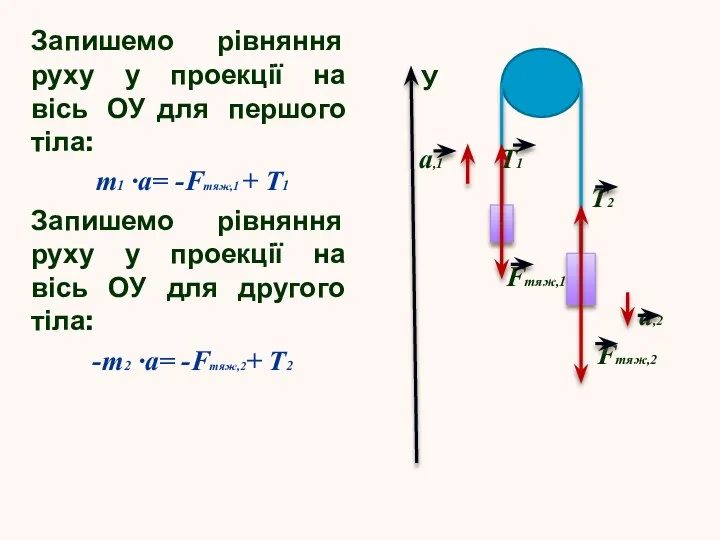
·a= -Fтяж,1 + Т1
Запишемо рівняння руху у проекції на вісь ОУ для другого тіла:
-m2 ·a= -Fтяж,2+ Т2
У
а,1 Т1
Т2
Fтяж,1
а,2
Fтяж,2
Слайд 9Гирі зв'язані нерозтяжною ниткою, тому їхні прискорення за модулем рівні, тобто:
| а1

| = | а1 | = а
Натяг нитки по обидві сторони блока однаковий, тоді:
|Т1 | = | Т2 | = Т
Врахуємо, що Fтяж = m·g розв'яжемо систему з двох рівнянь:
т1а = Т – m1·g,
-т2а = Т – m2·g







 Переходные процессы в электроэнергетических системах. Приведение магнитосвязанных цепей к одному уровню напряжения
Переходные процессы в электроэнергетических системах. Приведение магнитосвязанных цепей к одному уровню напряжения Расчет изгибаемых элементов по наклонным сечениям
Расчет изгибаемых элементов по наклонным сечениям Линзы. Ход лучей в линзах
Линзы. Ход лучей в линзах Решение задач БТ-21-1, ИСТ-21-1,2,3. Механика
Решение задач БТ-21-1, ИСТ-21-1,2,3. Механика Как измеряются разводы и чем
Как измеряются разводы и чем Косой изгиб. Построение эпюр нормальных напряжений по сечению при косом изгибе и внецентренном сжатии
Косой изгиб. Построение эпюр нормальных напряжений по сечению при косом изгибе и внецентренном сжатии Гармонические колебания. Амплитуда, период и частота колебательного движения
Гармонические колебания. Амплитуда, период и частота колебательного движения Циклы Карно
Циклы Карно Механические колебания и волны. Решение задач
Механические колебания и волны. Решение задач Ударная вязкость. Определение ударной вязкости
Ударная вязкость. Определение ударной вязкости Монтаж тамбура жилого дома краном КС-35714К3-10. Техническое обслуживание и ремонт карданной передачи УРАЛ
Монтаж тамбура жилого дома краном КС-35714К3-10. Техническое обслуживание и ремонт карданной передачи УРАЛ Гидродинамика
Гидродинамика Электростатика. Сила Кулона
Электростатика. Сила Кулона Термодинамика
Термодинамика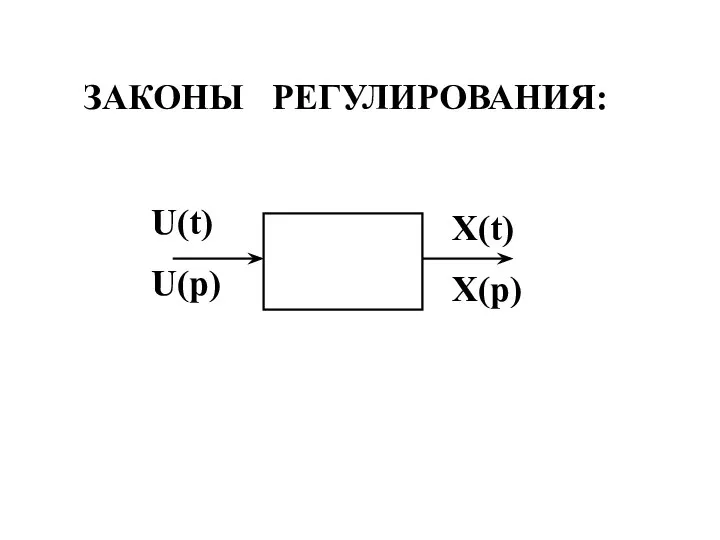 Законы регулирования
Законы регулирования Подготовка деталей к сборке
Подготовка деталей к сборке Презентация на тему Атмосферное давление: тест
Презентация на тему Атмосферное давление: тест  Генерирование электрической энергии. Трансформатор
Генерирование электрической энергии. Трансформатор Общий курс железных дорог. ОКЖД. Лекция 1
Общий курс железных дорог. ОКЖД. Лекция 1 Скорость витания
Скорость витания Изучение электрохимических свойств нанокристаллов
Изучение электрохимических свойств нанокристаллов Ситникова Надежда Александровна, Бормотова Ольга Владимировна, учителя физики БОУ СОШ № 10 МО Динской район
Ситникова Надежда Александровна, Бормотова Ольга Владимировна, учителя физики БОУ СОШ № 10 МО Динской район Криволинейное движение. Динамика
Криволинейное движение. Динамика Вес. Сила тяжести
Вес. Сила тяжести Удивительный транспорт. 3 класс
Удивительный транспорт. 3 класс Сверлильный станок
Сверлильный станок Презентация_по_МДК_02_01_Управление_коллективом_исполнителей_Виды
Презентация_по_МДК_02_01_Управление_коллективом_исполнителей_Виды Путешествие в страну физики. Урок-викторина, 7 класс
Путешествие в страну физики. Урок-викторина, 7 класс