Саха теңдеуі

Газды ең жоғары температураға дейін қыздыру арқылы плазма алуға болады. Ол кезде газ бөлшектері жоғары кинетикалық энергияға ие болып, бейтарап атомдармен соқтығысу нәтижесінде атом орбитасынан электронды жұлып шығарады. Сол кезде газ иондалып плазма пайда болады. Газдың иондалу дәрежесі температураға Т тәуелді, бірақ қалай деген сұрақ туындайды? Оның универсалды жауабын былай айтуға болады: қыздырылып иондалған газ термодинамикалық тепе-тең күйде деп болжайтын болсақ. Ол кезде статистикалық физика әдісін қолданып, ионизация процесін химиялық реакция ретінде қарастыруға болады. Енді сутегі атомының иондалуын қарастырайық.

Бастапқыда V көлемде Nа0 атом болсын. Ионизация нәтижесінде Nі ион және Nе электрон пайда болады. Nі=Nе;
Nа=Nа0-Nі қалған атом саны
Бір атомның ядросын(протон) қарастырайық. Егер оның айналасында байланысқан электрон болса, онда ол атом болады, ал кері жағдайда ол ион. Электрон энергия күйінде болуының ықтималдылығы

А- нормировтық константа
- электрон байланысқан күйде
- электрон еркін қозғалыста
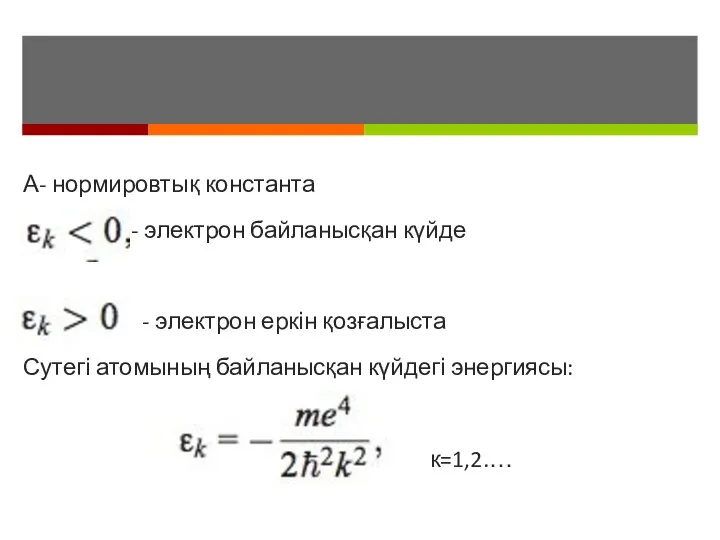
Сутегі атомының байланысқан күйдегі энергиясы:
к=1,2.…

Ең төмен деңгейді қолданамыз, к=1. Ол кезде
Электрон мынадай энергияға ие:
Немесе үздіксіз спектр қабылдайды.
I – шамасы сутегі атомының иондалу потенциалы деп аталады.

А-ны табу үшін электронның қандай да бір энергияға ие болуының толық ықтималдылығы бірге тең болсын:
Осыдан

Энергияны интегралға ауыстыру
арқылы біз квазиклассикалық жуықтауды қолданамыз, яғни электронның әрбір энергиялық күйіне фазалық кеңістіктегі қарапайым ұяшықтар сәйкес келеді. Үздіксіз спектрдің көп бөлігінде бұл энергия аз болып қалады. Онда еркін электронның энергиясы тең, бұл бізге интегралды
оңай шешуге мүмкіндік береді :

плазманың толық көлемінің еркін электрон санына қатынасына тең
Сонымен қатар де Бройль толқын ұзындығын енгіземіз:
Осыдан нормировтық константамыз келесі түрде болады:

қарастырып отырған протон бейтарап атомның ядросы болып табылады, яғни оған жақын жерде байланысқан электрон болуының ықтималдығы
Ал атом иондалуының ықтималдығы

Олардың қатынасы плазмадағы ион мен электрон тығыздықтарының қатынасын береді
Осыдан біз ион,электрон, атомның тығыздықтарын плазма температурасы арқылы өрнектейтін Саха формуласын аламыз:

Әрбір электронда, ионда және атомда ішкі еркіндік дәрежесі болады. Мысалы: электронның жоғары немесе төмен бағытталған спині болады. Ішкі еркіндік дәрежесінің болуы еркін электрондардың энергия деңгейін өзгертпейді және бір энергиялық деңгейде бірмезгілде екі электрон болуы мүмкін.. Осыған байланысты электронның статсалмағын енгіземіз ge. ge=2 болғандықтан деп біз электрон тығыздығын екі есе төмендеттік. Статсалмаққа ион мен атомда ие.

Плазманың иондалу дәрежесі :
–ядро тығыздығы