Содержание
- 2. Основные понятия Истинное значение физической величины ― идеальным образом характеризующее рассматриваемое свойство данного объекта как в
- 3. Лекция 2. Основные понятия теории погрешностей Погрешность средства измерений ― разность между показанием средства измерения и
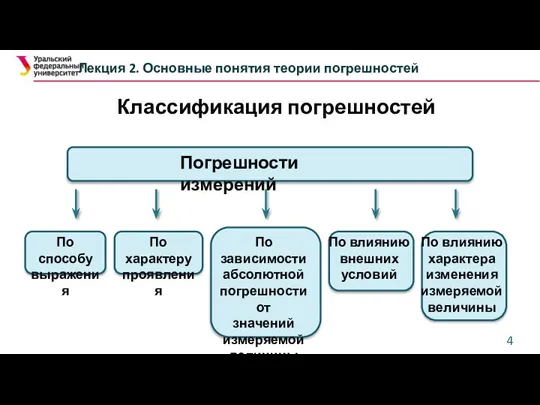
- 4. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей Погрешности измерений По способу выражения По характеру проявления
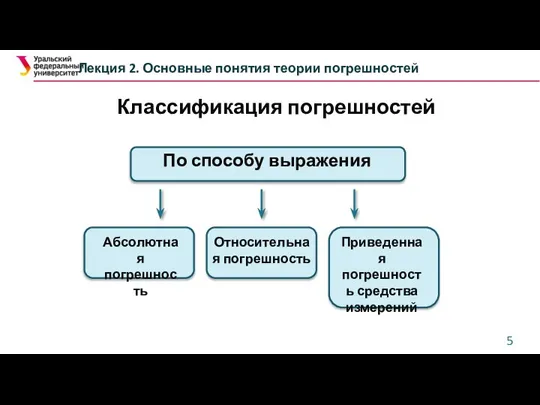
- 5. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По способу выражения Абсолютная погрешность Приведенная погрешность средства
- 6. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей Абсолютная погрешность ― разница между результатом измерения X
- 7. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей Приведенная погрешность средства измерений ― относительная погрешность, в
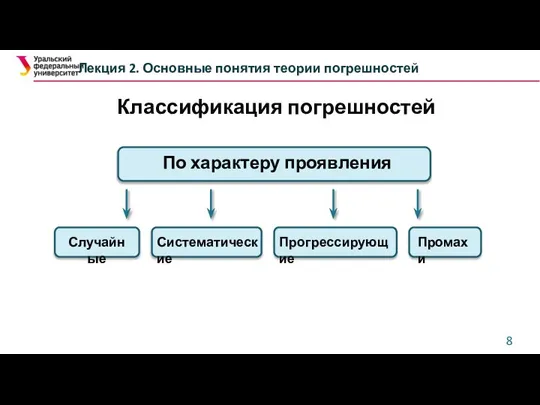
- 8. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По характеру проявления Случайные Систематические Прогрессирующие Промахи
- 9. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По характеру проявления Случайная погрешность – составляющая погрешности
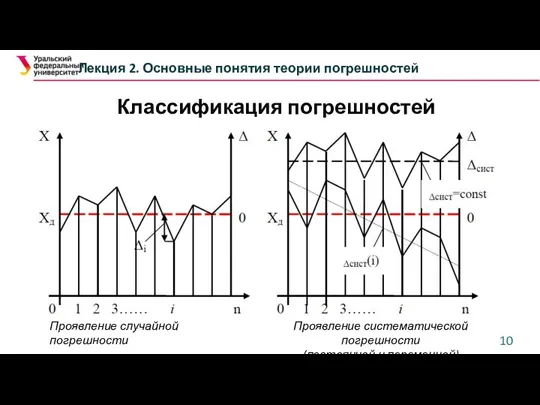
- 10. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По характеру проявления Проявление случайной погрешности Проявление систематической
- 11. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По характеру проявления Прогрессирующая (дрейфовая) погрешность – это
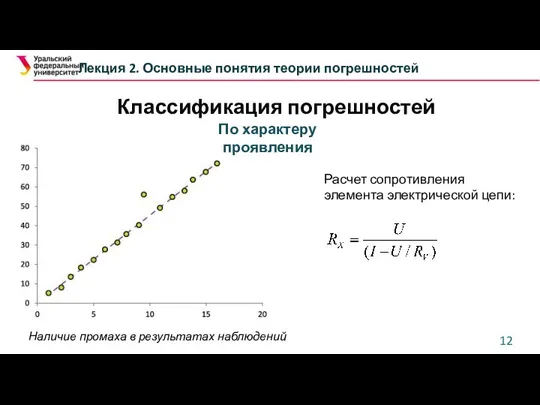
- 12. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По характеру проявления http://www.ngpedia.ru/id271377p2.html Наличие промаха в результатах
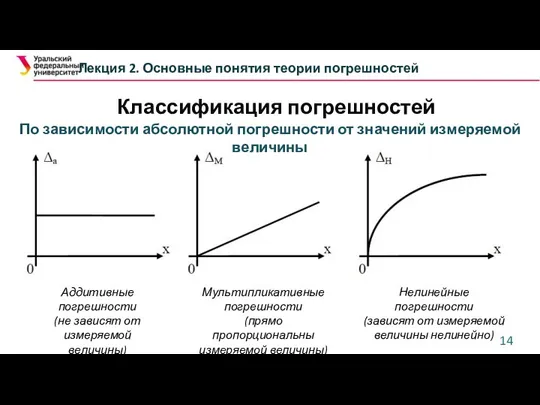
- 13. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По зависимости абсолютной погрешности от значений измеряемой величины
- 14. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По зависимости абсолютной погрешности от значений измеряемой величины
- 15. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей http://www.ngpedia.ru/id271377p2.html
- 16. Обозначение классов точности Лицевая панель амперметра класса точности 1,5 с равномерной шкалой Лекция 2. Основные понятия
- 17. Обозначение классов точности Лицевая панель ампервольтметра класса точности 0,02/0,01 с равномерной шкалой Лекция 2. Основные понятия
- 18. Обозначение классов точности Лицевая панель мегаомметра класса точности 2,5 Лекция 2. Основные понятия теории погрешностей Классификация
- 19. Обозначение классов точности Лицевая панель фазометра класса точности 1,0 с существенно неравномерной шкалой Лекция 2. Основные
- 20. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По влиянию внешних условий Основные погрешности Дополнительные погрешности
- 21. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По влиянию внешних условий http://www.ngpedia.ru/id271377p2.html Основная погрешность средства
- 22. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По влиянию внешних условий http://www.ngpedia.ru/id271377p2.html Нормальные условия, как
- 23. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей По влиянию внешних условий http://www.ngpedia.ru/id271377p2.html – дополнительная погрешность,
- 24. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей В зависимости от влияния характера изменения измеряемых величин
- 25. Классификация погрешностей Лекция 2. Основные понятия теории погрешностей В зависимости от влияния характера изменения измеряемых величин
- 26. Правила представления результатов измерений Лекция 2. Основные понятия теории погрешностей Значащие цифры данного числа – все
- 27. Правила представления результатов измерений Лекция 2. Основные понятия теории погрешностей Значащие цифры приближенного числа называются верными,
- 28. Лекция 2. Основные понятия теории погрешностей 1. В случае, если первая из отбрасываемых цифр (считая слева
- 29. Лекция 2. Основные понятия теории погрешностей 2. В случае, если первая из отбрасываемых цифр (считая слева
- 30. Лекция 2. Основные понятия теории погрешностей 3. В случае, если первая из отбрасываемых цифр равна 5
- 31. Лекция 2. Основные понятия теории погрешностей 4. При записи результата измерения на первом этапе округляются погрешности
- 32. Лекция 2. Основные понятия теории погрешностей 5. Далее округляется само числовое значение ФВ, причем ее количество
- 33. Лекция 2. Основные понятия теории погрешностей 6. Если при округлении погрешности указан порядок, т.е. 10n, то
- 34. Правила представления результатов измерений Лекция 2. Основные понятия теории погрешностей Возведение в степень и извлечение корня
- 35. Примеры заданий Лекция 2. Основные понятия теории погрешностей 1. Число 83,26 найдено с относительной погрешностью 0,3%.
- 36. Примеры заданий Лекция 2. Основные понятия теории погрешностей 1. Число 83,26 найдено с относительной погрешностью 0,3%.
- 37. Лекция 2. Основные понятия теории погрешностей 2. Найти абсолютные и относительные погрешности числа е = 2,71828182…,
- 38. Лекция 2. Основные понятия теории погрешностей 2. Найти абсолютные и относительные погрешности числа е = 2,71828182…,
- 39. Лекция 2. Основные понятия теории погрешностей 3. Округлить число x = 4,45575250 до шести, пяти и
- 40. Лекция 2. Основные понятия теории погрешностей 3. Округлить число x = 4,45575250 до шести, пяти и
- 41. Лекция 2. Основные понятия теории погрешностей 4. Вычислить верные значащие цифры чисел. http://genphys.phys.msu.ru/rus/ofp/CanYouRound.pdf Примеры заданий Х
- 42. Лекция 2. Основные понятия теории погрешностей 4. Вычислить верные значащие цифры чисел. http://genphys.phys.msu.ru/rus/ofp/CanYouRound.pdf Х = 0,004507
- 43. Лекция 2. Основные понятия теории погрешностей 5. Получено значение физической величины 2,32540874 с погрешностью 0,162875. Записать
- 44. Лекция 2. Основные понятия теории погрешностей 5. Получено значение физической величины 2,32540874 с погрешностью 0,162875. Записать
- 45. Оценка погрешностей при косвенных измерениях Лекция 2. Основные понятия теории погрешностей http://genphys.phys.msu.ru/rus/ofp/CanYouRound.pdf Пусть представляющая интерес величина
- 46. Оценка погрешностей при косвенных измерениях Лекция 2. Основные понятия теории погрешностей http://genphys.phys.msu.ru/rus/ofp/CanYouRound.pdf Рассмотрим частные производные функции
- 47. Оценка погрешностей при косвенных измерениях Лекция 2. Основные понятия теории погрешностей http://genphys.phys.msu.ru/rus/ofp/CanYouRound.pdf Формулы расчета погрешностей для
- 48. Оценка погрешностей при косвенных измерениях Лекция 2. Основные понятия теории погрешностей http://genphys.phys.msu.ru/rus/ofp/CanYouRound.pdf Формулы расчета погрешностей для
- 49. Лекция 2. Основные понятия теории погрешностей 1. Размеры прямоугольника составляют а=3,3±0,1 см и b=5,2±0,1 см. Найти
- 50. Лекция 2. Основные понятия теории погрешностей 1. Размеры прямоугольника составляют а=3,3±0,1 см и b=5,2±0,1 см. Найти
- 51. Лекция 2. Основные понятия теории погрешностей 2. Дан цилиндр массой m=60,01±0,01 г, диаметром d=25,010±0,005 мм и
- 53. Скачать презентацию












































 Законы сохранения в механике. Решение задач
Законы сохранения в механике. Решение задач Особенности конструкции элементов системы неавтоматического управления
Особенности конструкции элементов системы неавтоматического управления Расчёт массы и объёма тела по его плотности. 7 класс
Расчёт массы и объёма тела по его плотности. 7 класс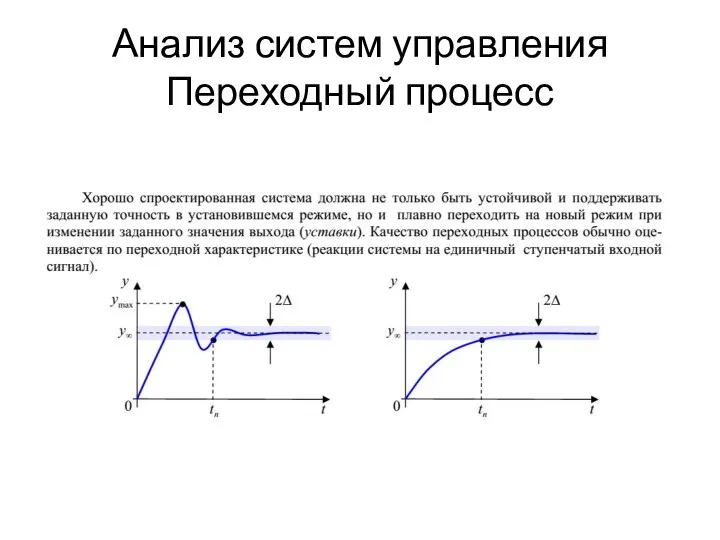 Анализ систем управления. Переходный процесс. ТАУ 5
Анализ систем управления. Переходный процесс. ТАУ 5 Как устроен атом
Как устроен атом В.А. Грибов. Я сдам ЕГЭ. Физика
В.А. Грибов. Я сдам ЕГЭ. Физика Порівняння роботи рухомого складу за різними видами тяги
Порівняння роботи рухомого складу за різними видами тяги Определение массы небесных тел
Определение массы небесных тел Презентация на тему Трение в природе и технике
Презентация на тему Трение в природе и технике 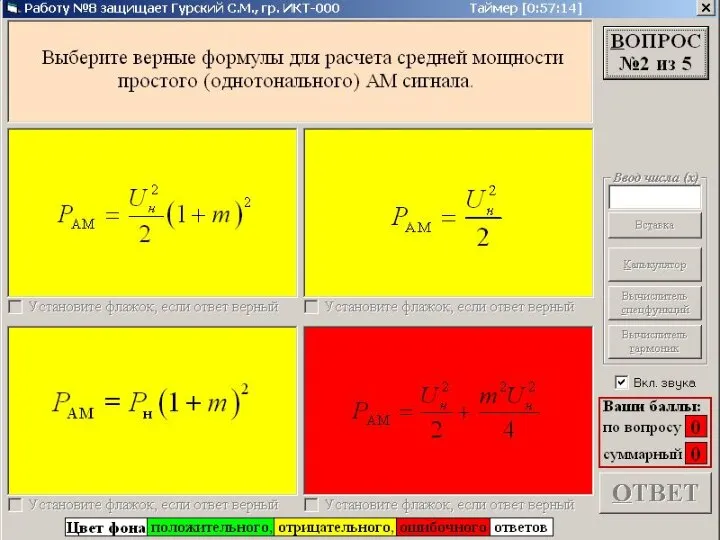 АМ БМ ОМ - математические модели сигналов. Тест
АМ БМ ОМ - математические модели сигналов. Тест Презентация на тему Сила упругости. Закон Гука. Вес тела
Презентация на тему Сила упругости. Закон Гука. Вес тела  Теорема Гаусса
Теорема Гаусса Реконструкция установки производства фталевого ангидрида
Реконструкция установки производства фталевого ангидрида Airbus 320 A. C.T. (Airbus Competence Training)
Airbus 320 A. C.T. (Airbus Competence Training) Электромагнитные излучения
Электромагнитные излучения Последовательное соединение
Последовательное соединение Парадоксы квантовой механики. Вселенная как она есть: Бог, время, человек
Парадоксы квантовой механики. Вселенная как она есть: Бог, время, человек Исследовательская работа на тему: Изучение плотности веществ
Исследовательская работа на тему: Изучение плотности веществ Простые механизмы
Простые механизмы Спектрометрия ультрафиолетовой и видимой части спектра
Спектрометрия ультрафиолетовой и видимой части спектра Сила тяжести. Сила упругости. Вес тела
Сила тяжести. Сила упругости. Вес тела Магнитное поле электрического тока
Магнитное поле электрического тока Бином Ньютона. 11 класс
Бином Ньютона. 11 класс Удельная теплоемкость
Удельная теплоемкость LT-система физических единиц
LT-система физических единиц Характеристики катера Амур-М
Характеристики катера Амур-М Цепная передача
Цепная передача Динамика судна. Общие понятия гидромеханики
Динамика судна. Общие понятия гидромеханики