Содержание
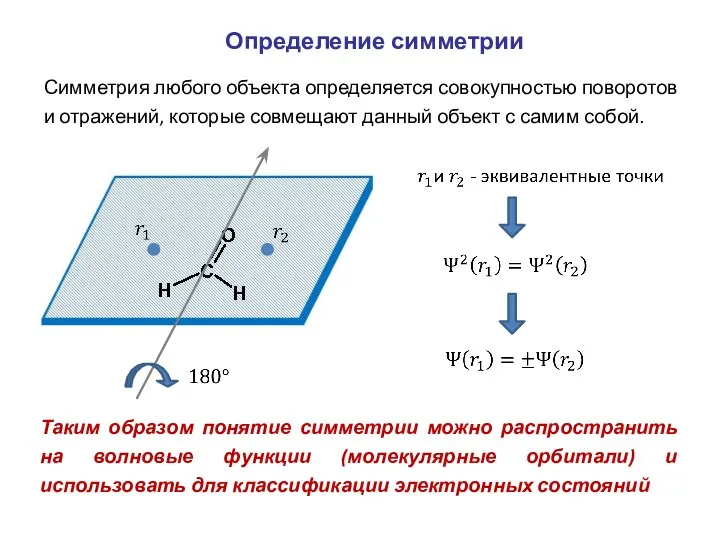
- 2. Определение симметрии Симметрия любого объекта определяется совокупностью поворотов и отражений, которые совмещают данный объект с самим
- 3. Определение симметрии Количественно симметрия характеризуется: Элементами симметрии Операциями симметрии Операции симметрии - это действие над объектом
- 4. Элементы и операции симметрии
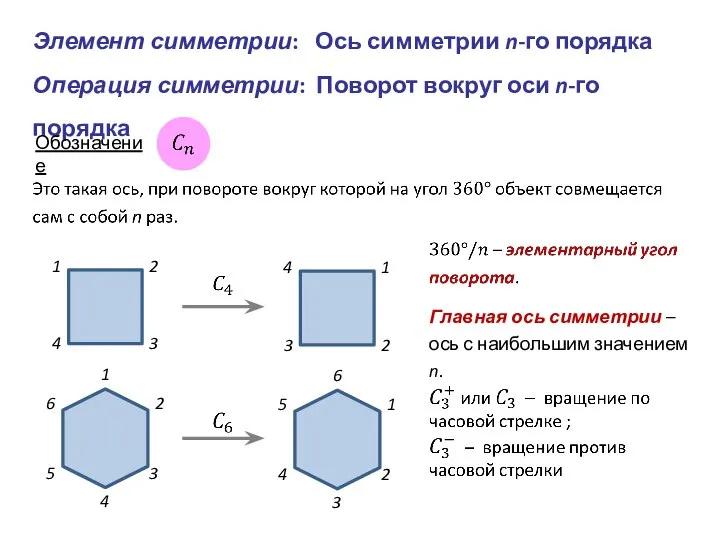
- 5. Элемент симметрии: Ось симметрии n-го порядка Операция симметрии: Поворот вокруг оси n-го порядка Обозначение 1 2
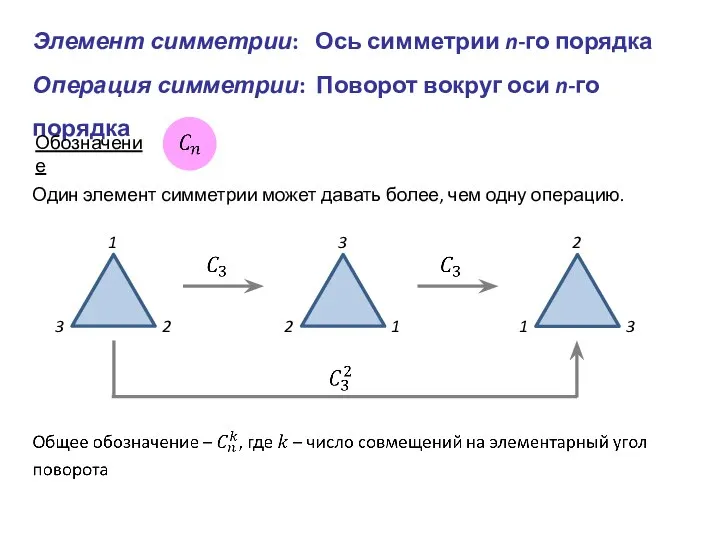
- 6. Элемент симметрии: Ось симметрии n-го порядка Операция симметрии: Поворот вокруг оси n-го порядка Обозначение Один элемент
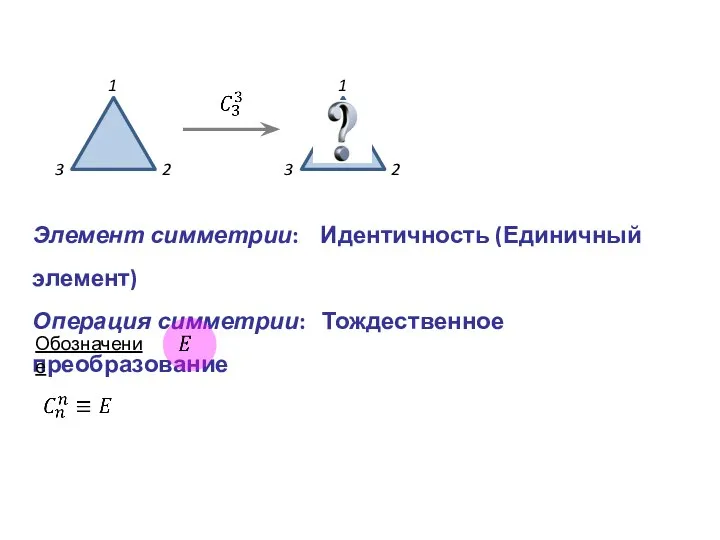
- 7. Элемент симметрии: Идентичность (Единичный элемент) Операция симметрии: Тождественное преобразование Обозначение 1 2 3 1 2 3
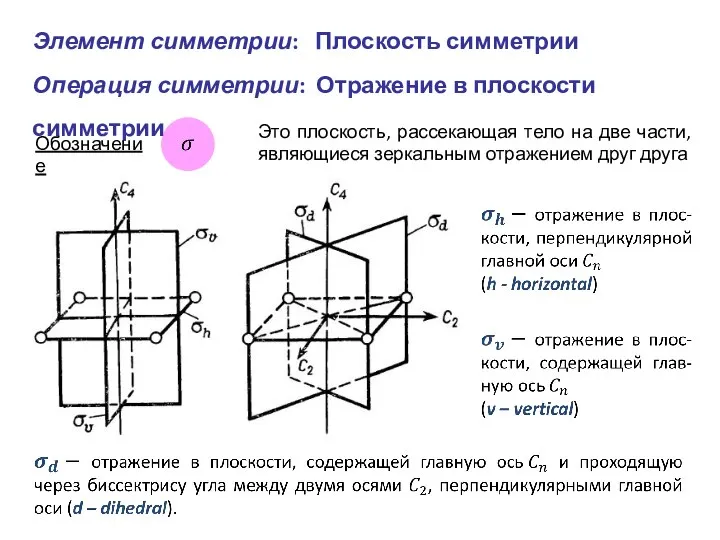
- 8. Элемент симметрии: Плоскость симметрии Операция симметрии: Отражение в плоскости симметрии Обозначение Это плоскость, рассекающая тело на
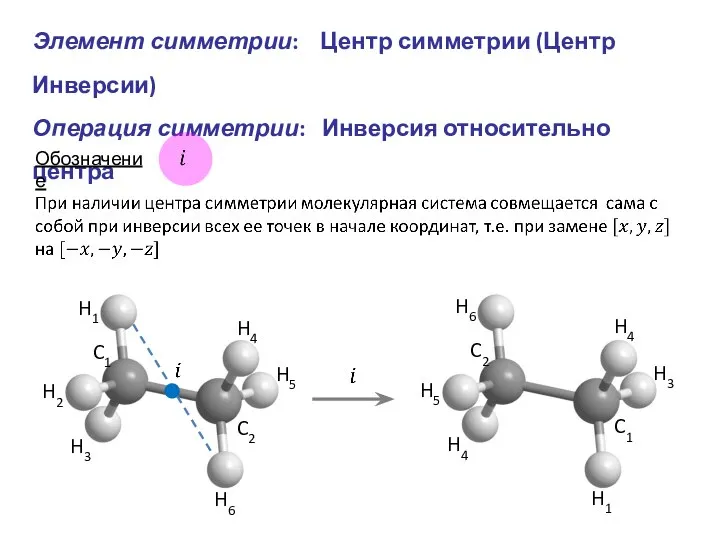
- 9. Элемент симметрии: Центр симметрии (Центр Инверсии) Операция симметрии: Инверсия относительно центра Обозначение H1 C2 H3 H2
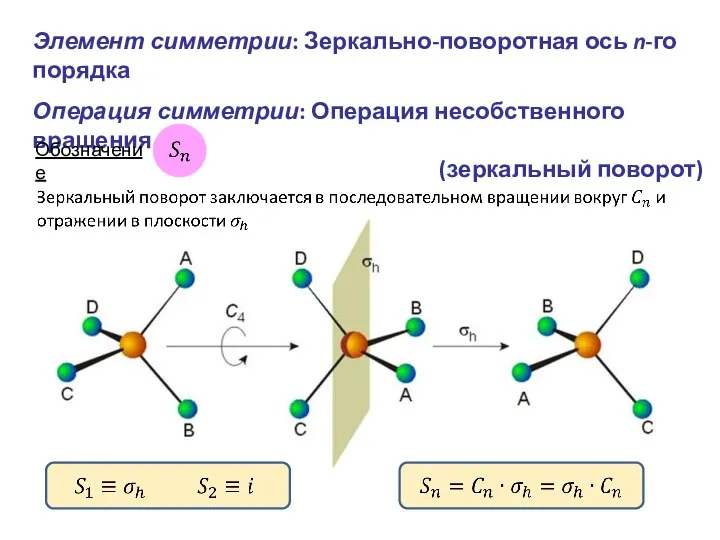
- 10. Элемент симметрии: Зеркально-поворотная ось n-го порядка Операция симметрии: Операция несобственного вращения (зеркальный поворот) Обозначение
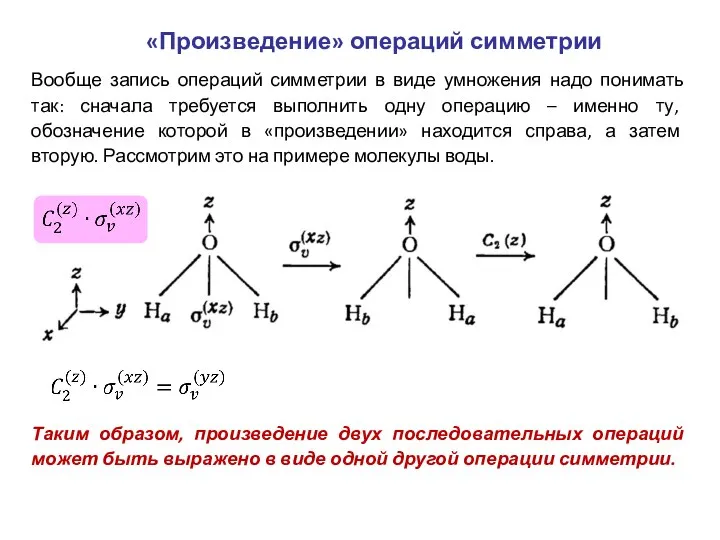
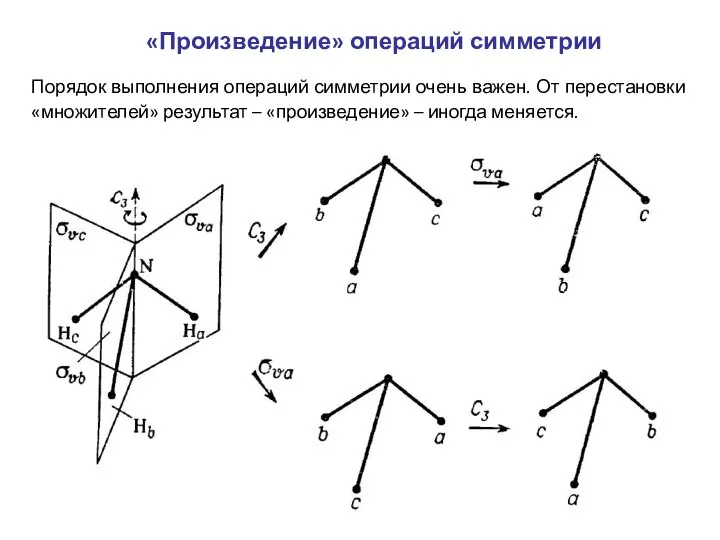
- 11. «Произведение» операций симметрии Вообще запись операций симметрии в виде умножения надо понимать так: сначала требуется выполнить
- 12. «Произведение» операций симметрии Порядок выполнения операций симметрии очень важен. От перестановки «множителей» результат – «произведение» –
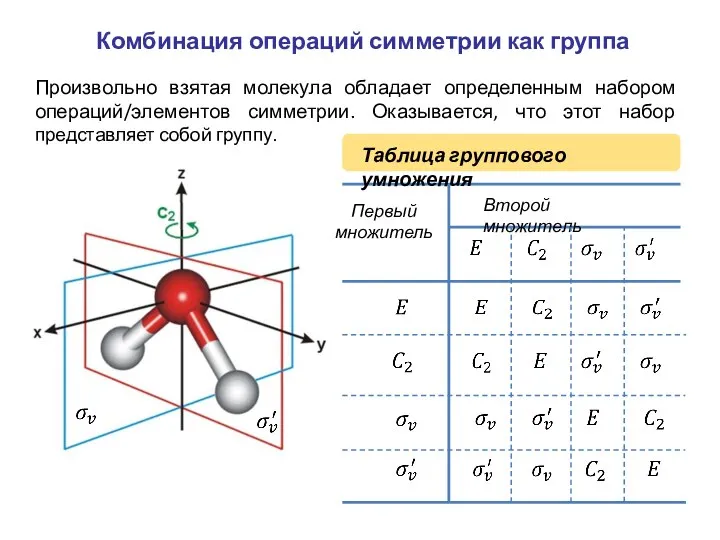
- 13. Комбинация операций симметрии как группа Произвольно взятая молекула обладает определенным набором операций/элементов симметрии. Оказывается, что этот
- 14. Математическое представление операций симметрии
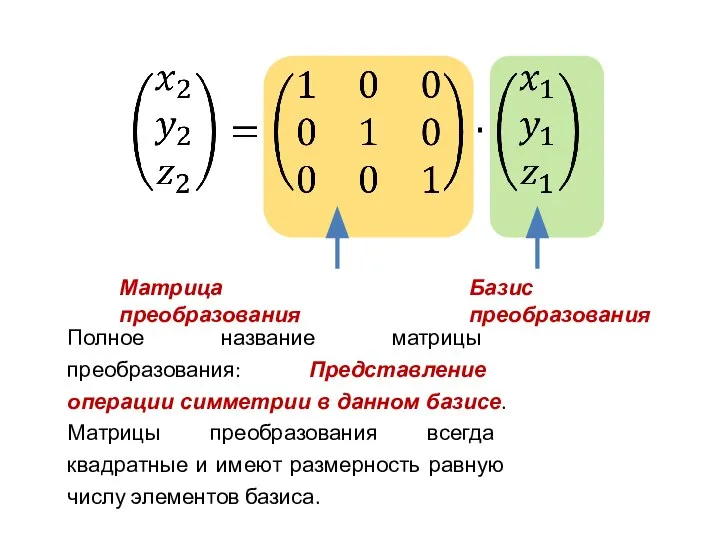
- 16. Матрица преобразования Базис преобразования Полное название матрицы преобразования: Представление операции симметрии в данном базисе. Матрицы преобразования
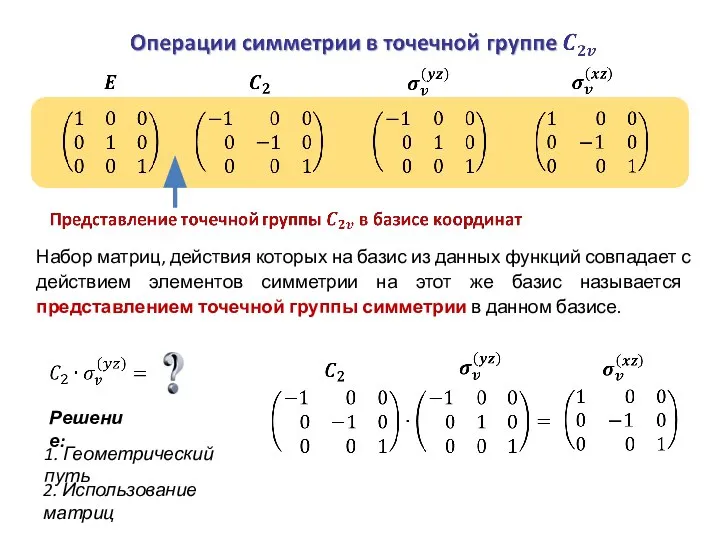
- 20. Набор матриц, действия которых на базис из данных функций совпадает с действием элементов симметрии на этот
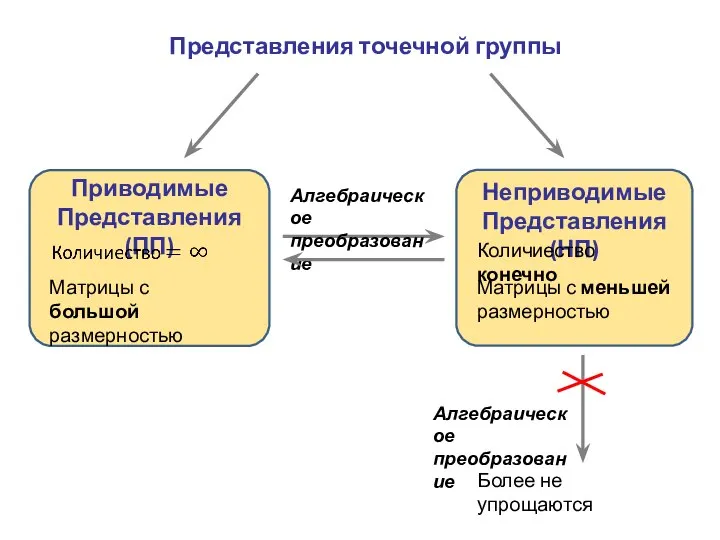
- 24. Представления точечной группы Приводимые Представления (ПП) Неприводимые Представления (НП) Матрицы с большой размерностью Алгебраическое преобразование Количиество
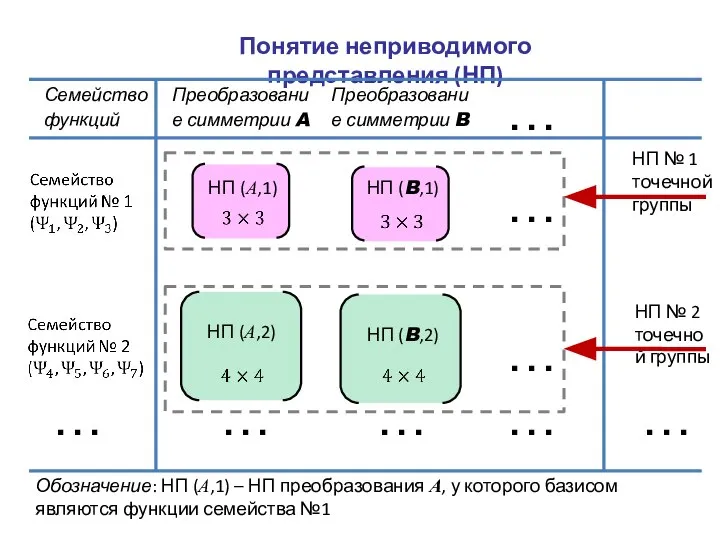
- 25. Понятие неприводимого представления (НП) Преобразование симметрии A ... ... ... ... ... ...
- 26. Коэффициенты равные нулю Понятие неприводимого представления (НП)
- 27. Преобразование симметрии A Преобразование симметрии B Семейство функций Понятие неприводимого представления (НП) … … … …
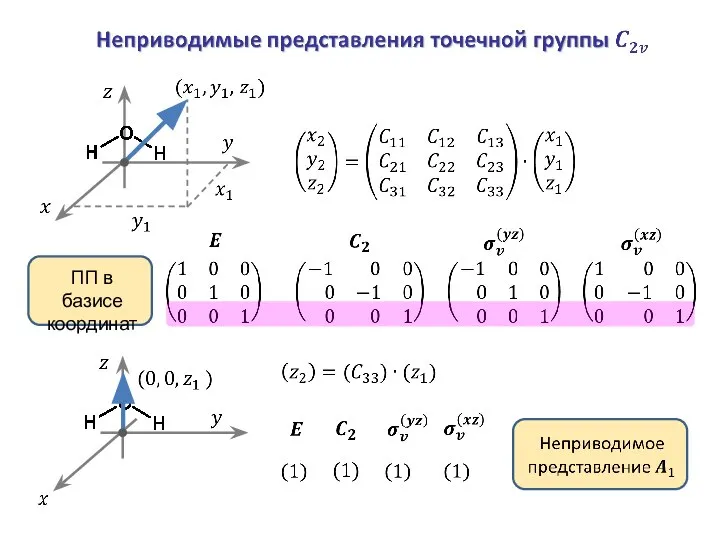
- 28. ПП в базисе координат
- 29. ПП в базисе координат
- 30. ПП в базисе координат
- 31. Неприводимые представления некоторых точечных групп симметрии
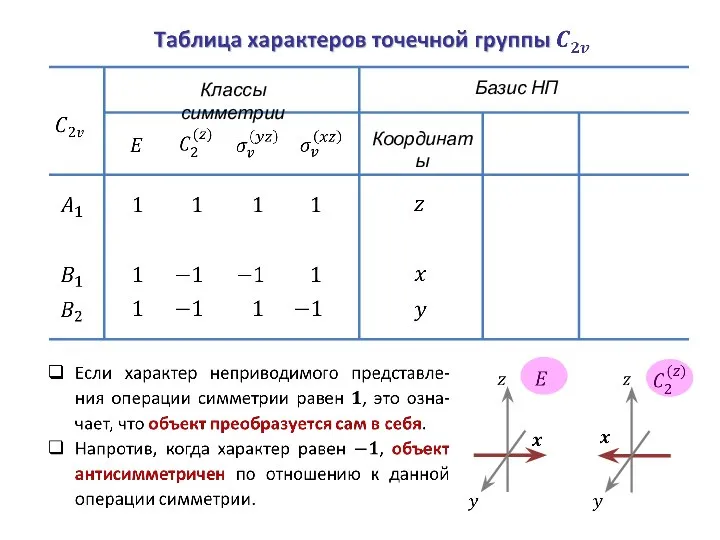
- 32. Таблицы характеров неприводимых представлений
- 33. Это сумма ее диагональных элементов. Характер матрицы
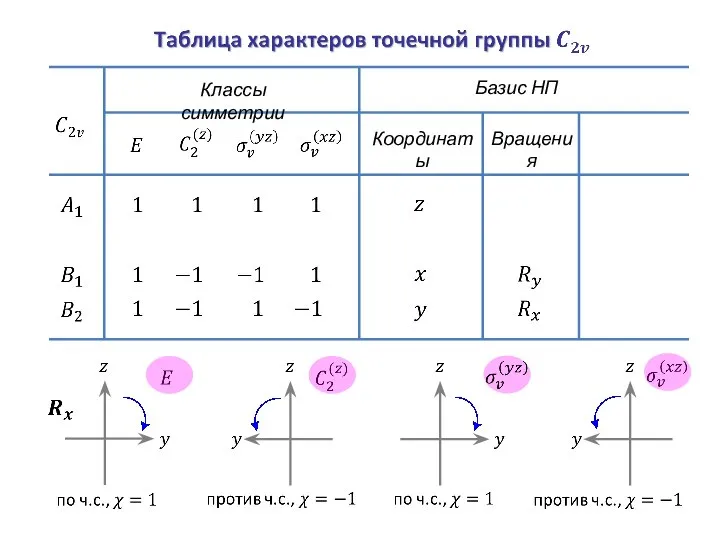
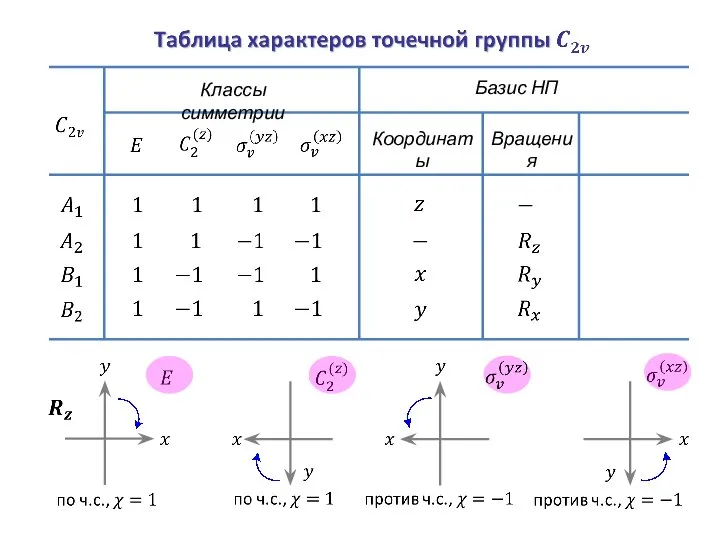
- 34. Классы симметрии Базис НП Координаты
- 35. Классы симметрии Базис НП Координаты Вращения
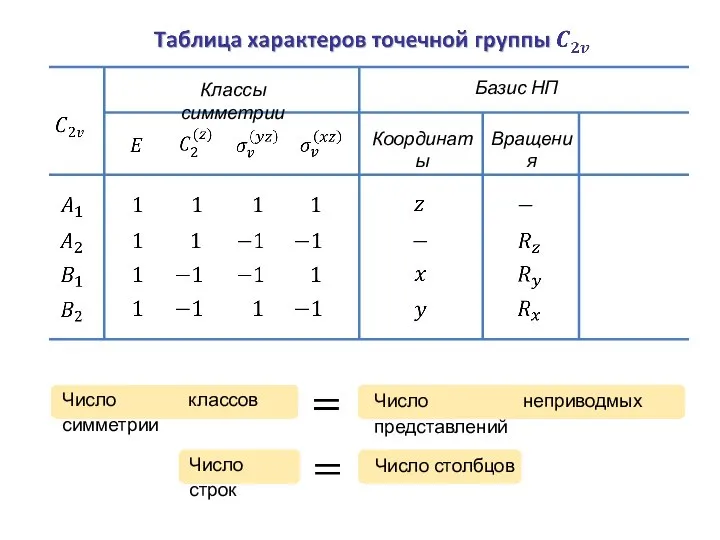
- 36. Классы симметрии Базис НП Координаты Вращения Число классов симметрии Число неприводмых представлений Число строк Число столбцов
- 37. Классы симметрии Базис НП Координаты Вращения
- 38. Функции Классы симметрии Базис НП Координаты Вращения
- 40. Поэтому любая молекулярная орбиталь молекулы обязательно будет соответствовать одному из неприводимых представлений точечной группы, к которой
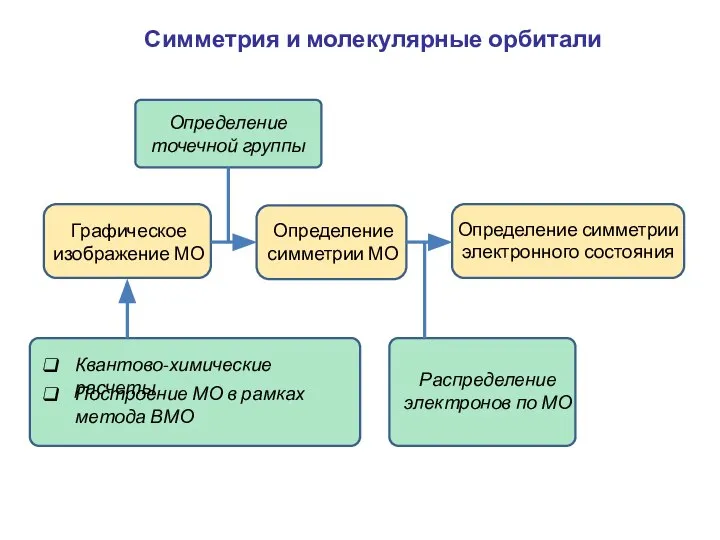
- 41. Симметрия и молекулярные орбитали Графическое изображение МО Квантово-химические расчеты Построение МО в рамках метода ВМО Определение
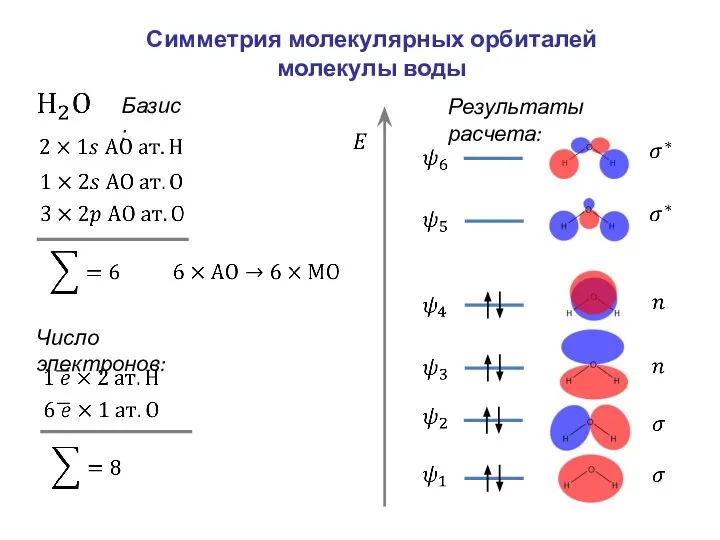
- 42. Симметрия молекулярных орбиталей молекулы воды Базис: Результаты расчета: Число электронов:
- 43. Симметрия молекулярных орбиталей молекулы воды НП МО
- 44. Определение симметрии состояний молекулы воды. Прямое произведение представлений Прямое произведение НП:
- 45. Определение симметрии состояний молекулы воды. Прямое произведение представлений Прямое произведение НП:
- 46. Обозначения неприводимых представлений по Малликену
- 47. Обозначения неприводимых представлений по Малликену
- 48. Электронные конфигурации и электронные состояния
- 49. Электронная конфигурация – распределение электронов по орбиталям в системе Электронное состояние – те свойства системы, которые
- 50. Спин электрона
- 51. Спиновые характеристики многоэлектронной системы Для данной электронной конфигурации:
- 52. Система с замкнутой электронной оболочкой Система с незамкнутой электронной оболочкой (радикал, ион-радикал) Синглетное состояние (обозначается S)
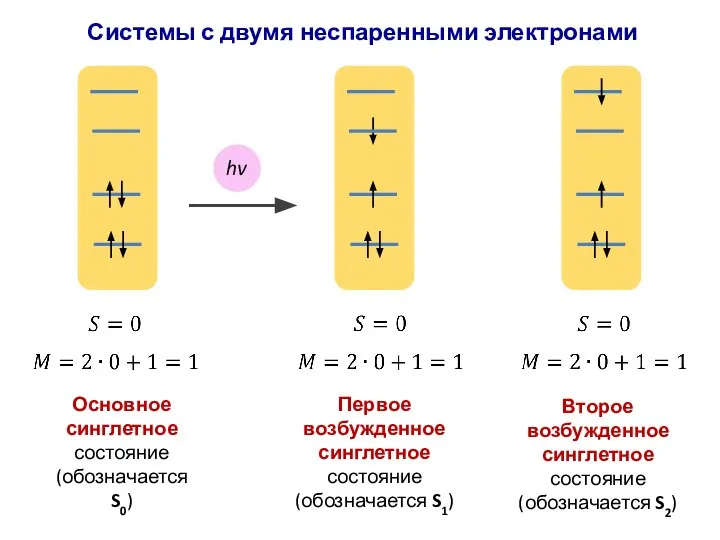
- 53. Основное синглетное состояние (обозначается S0) hv Первое возбужденное синглетное состояние (обозначается S1) Системы с двумя неспаренными
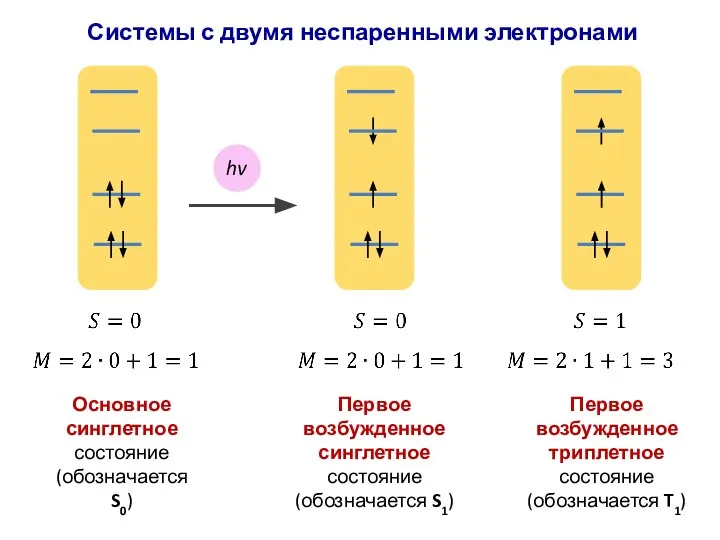
- 54. Основное синглетное состояние (обозначается S0) hv Первое возбужденное синглетное состояние (обозначается S1) Первое возбужденное триплетное состояние
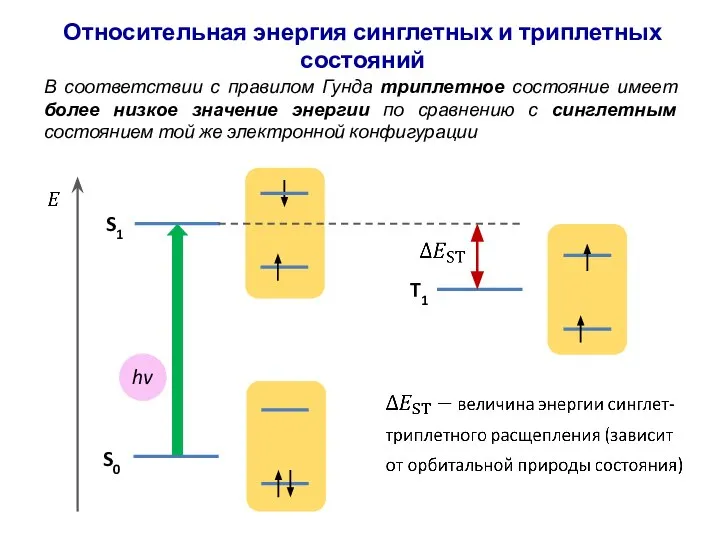
- 55. В соответствии с правилом Гунда триплетное состояние имеет более низкое значение энергии по сравнению с синглетным
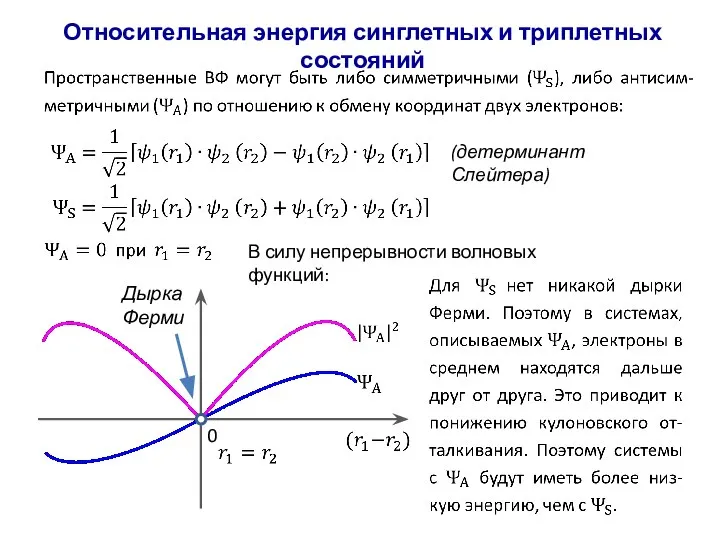
- 56. Относительная энергия синглетных и триплетных состояний В силу непрерывности волновых функций: 0 Дырка Ферми (детерминант Слейтера)
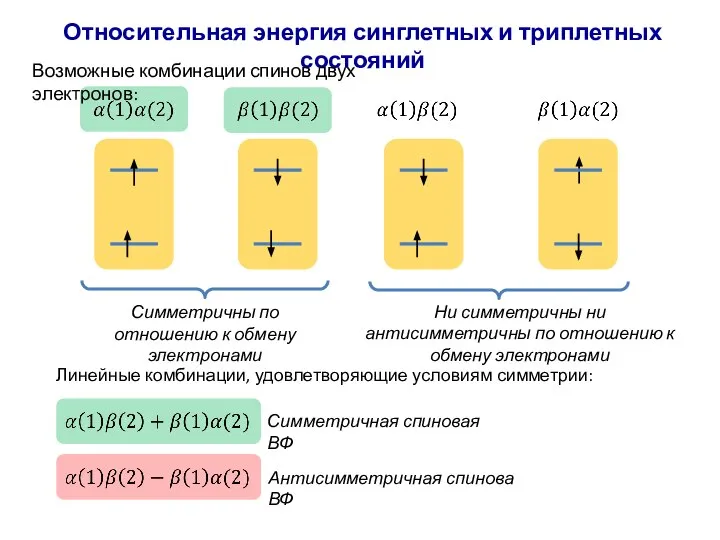
- 57. Относительная энергия синглетных и триплетных состояний Возможные комбинации спинов двух электронов: Симметричны по отношению к обмену
- 58. Относительная энергия синглетных и триплетных состояний Триплетная спиновая ВФ (симметричная) Синглетная спиновая ВФ (антисимметрияная) Поэтому у
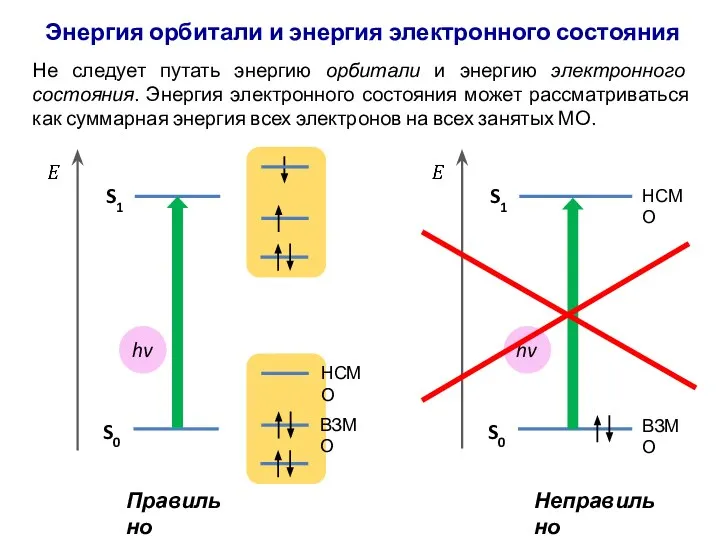
- 59. Энергия орбитали и энергия электронного состояния Не следует путать энергию орбитали и энергию электронного состояния. Энергия
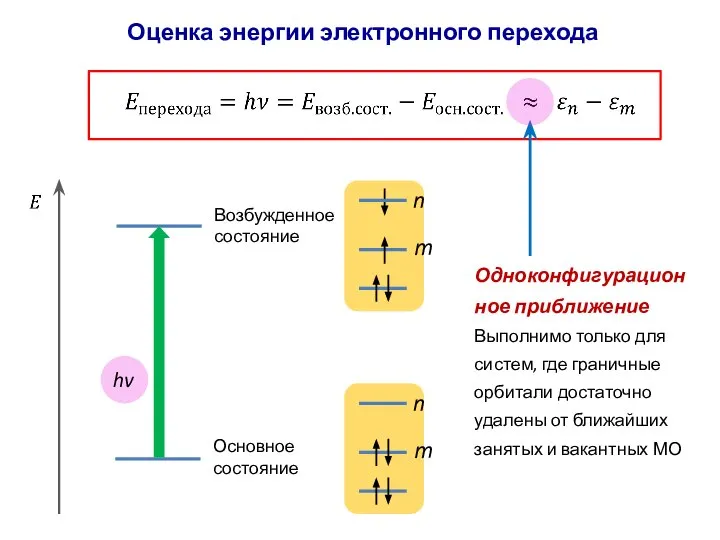
- 60. Оценка энергии электронного перехода hv m n Основное состояние Возбужденное состояние Одноконфигурационное приближение Выполнимо только для
- 61. Вероятность, поляризация и правила отбора электронных переходов
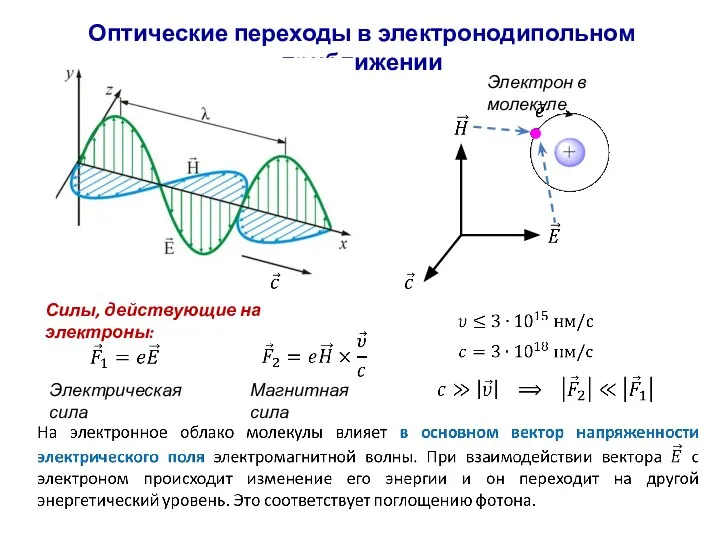
- 62. Оптические переходы в электронодипольном приближении Силы, действующие на электроны: Электрон в молекуле Электрическая сила Магнитная сила
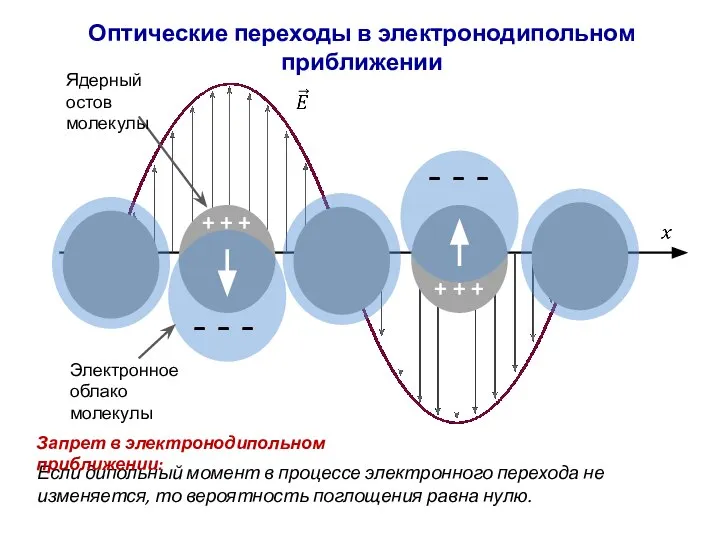
- 63. Оптические переходы в электронодипольном приближении - - - - - - + + + + +
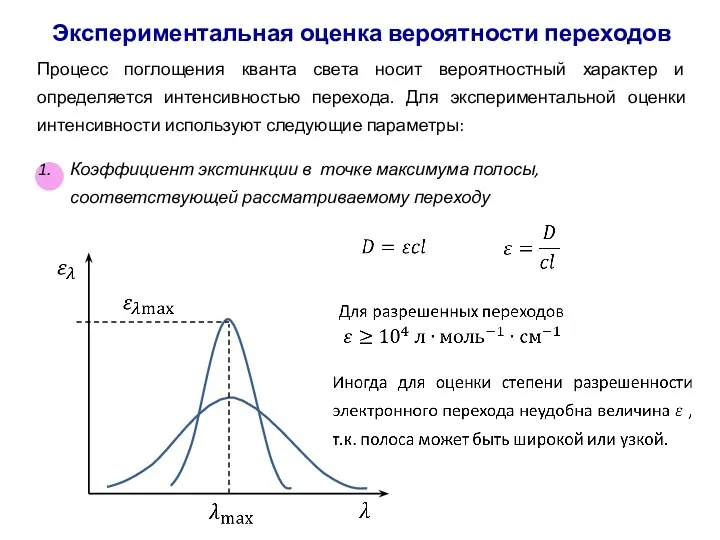
- 64. Процесс поглощения кванта света носит вероятностный характер и определяется интенсивностью перехода. Для экспериментальной оценки интенсивности используют
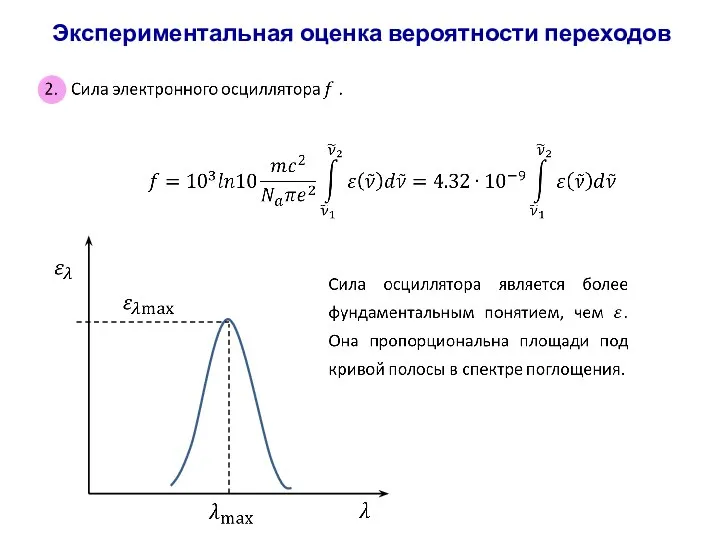
- 65. Экспериментальная оценка вероятности переходов
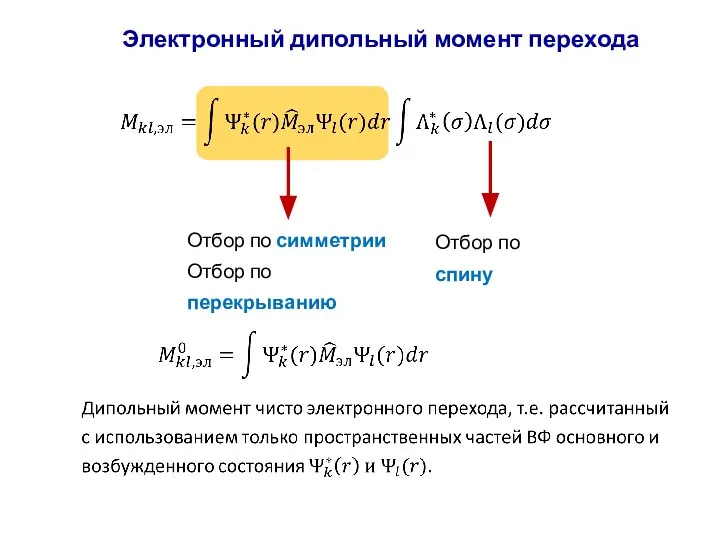
- 66. Интеграл момента перехода (дипольный момент перехода) Матричный элемент момента перехода Дипольный момент молекулы в основном электронном
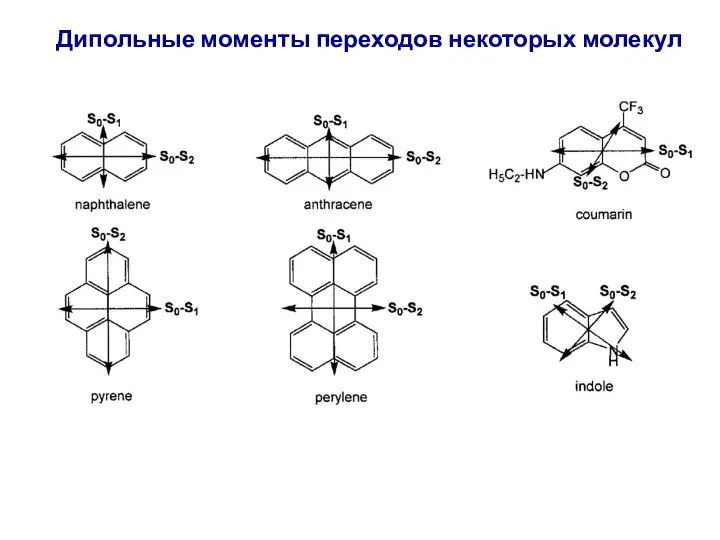
- 67. Дипольные моменты переходов некоторых молекул
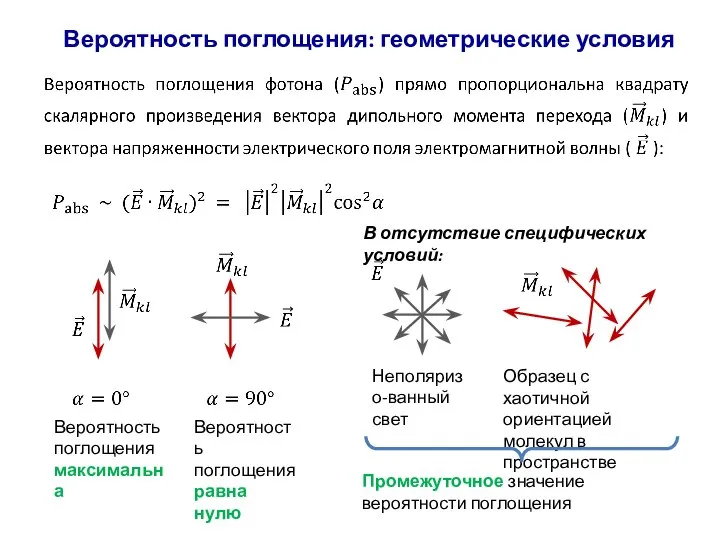
- 68. Вероятность поглощения: геометрические условия Неполяризо-ванный свет Образец с хаотичной ориентацией молекул в пространстве Вероятность поглощения максимальна
- 69. Правила отбора для электронно-колебательных переходов (Приближение Борна-Оппенгеймера)
- 70. Важное свойство электронных волновых функций Таким образом, электронные волновые функции ортонормированы Ядерные волновые функции ортонормированными не
- 71. Правила отбора для электронно-колебательных переходов (Приближение Борна-Оппенгеймера)
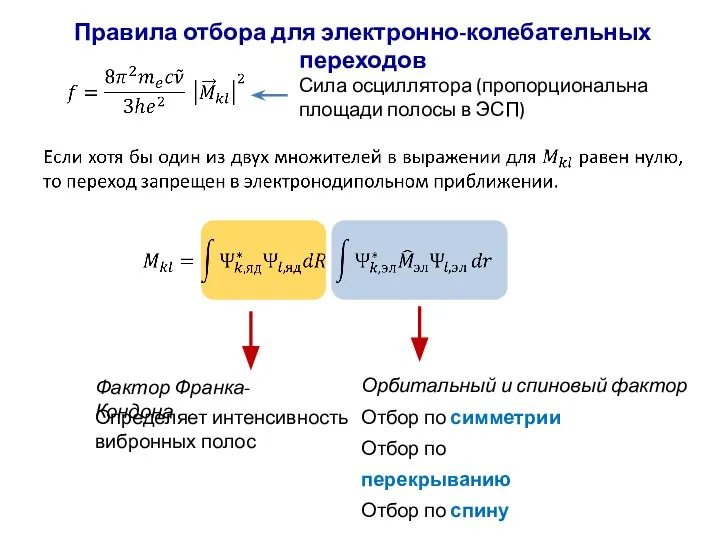
- 72. Правила отбора для электронно-колебательных переходов Фактор Франка-Кондона Отбор по симметрии Отбор по перекрыванию Отбор по спину
- 73. Отбор по спину Спиновые волновые функции предполагаются ортонормированными:
- 74. Отбор по спину Отбор по спину
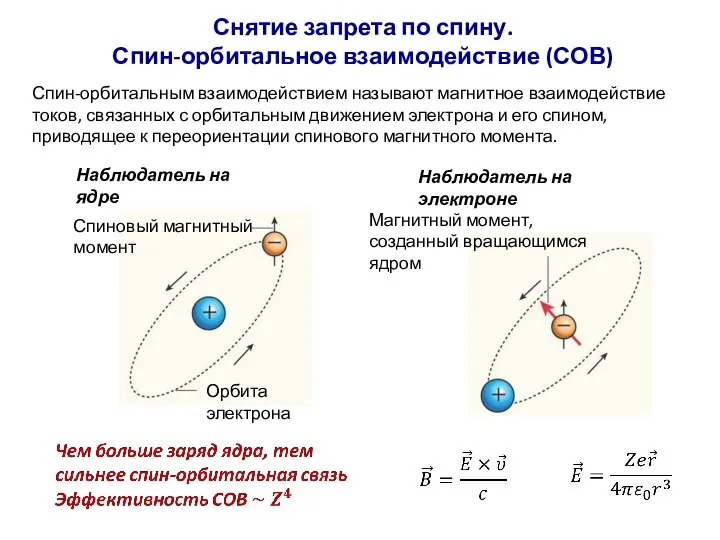
- 75. Снятие запрета по спину. Спин-орбитальное взаимодействие (СОВ) Спиновый магнитный момент Орбита электрона Наблюдатель на ядре Спин-орбитальным
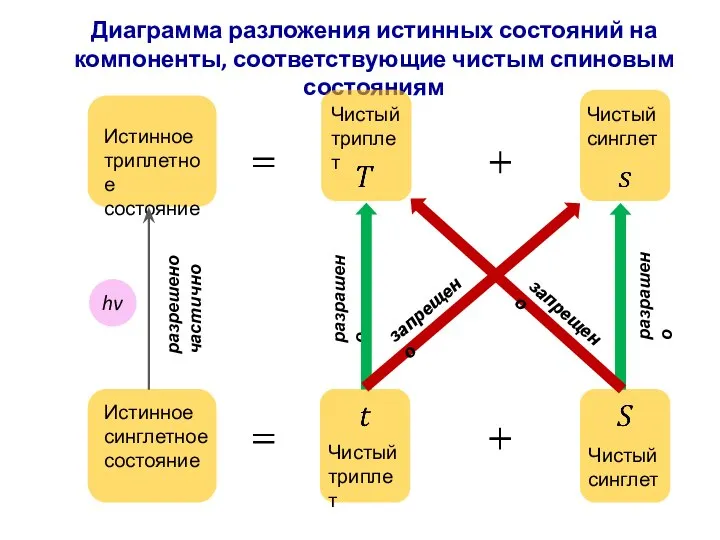
- 76. Диаграмма разложения истинных состояний на компоненты, соответствующие чистым спиновым состояниям
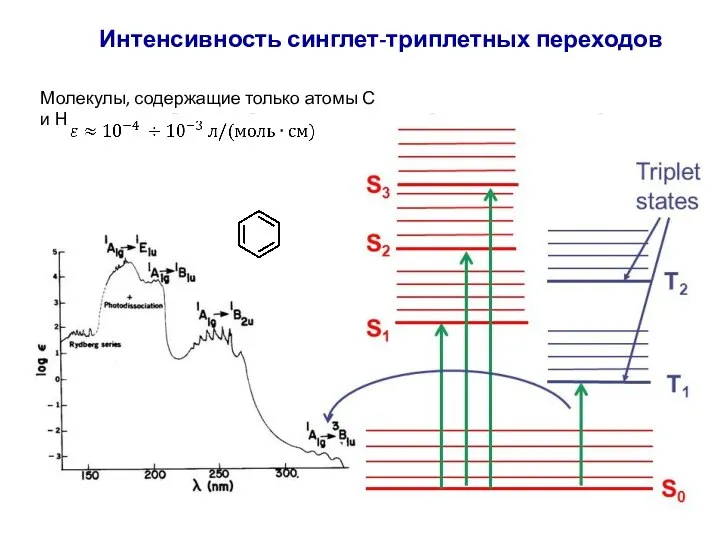
- 77. Интенсивность синглет-триплетных переходов Молекулы, содержащие только атомы С и Н
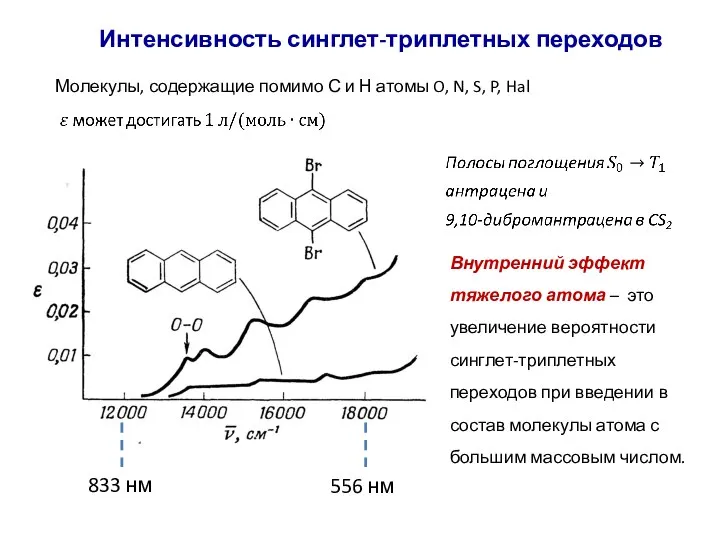
- 78. Молекулы, содержащие помимо С и Н атомы O, N, S, P, Hal 833 нм Интенсивность синглет-триплетных
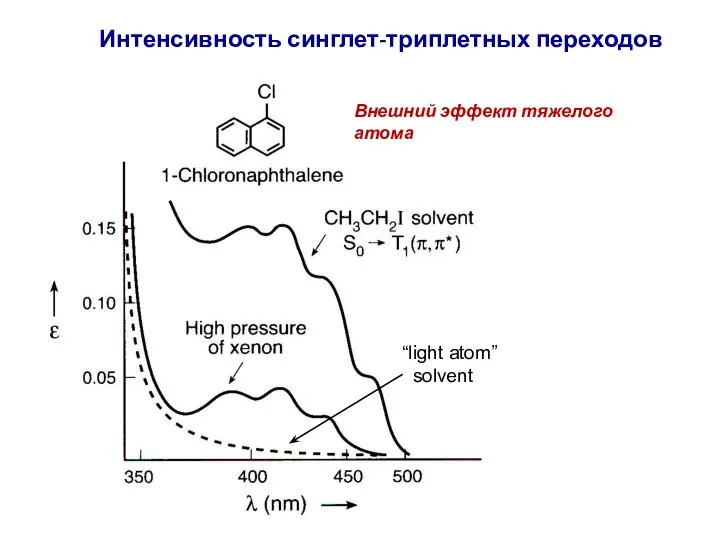
- 79. Интенсивность синглет-триплетных переходов “light atom” solvent Внешний эффект тяжелого атома
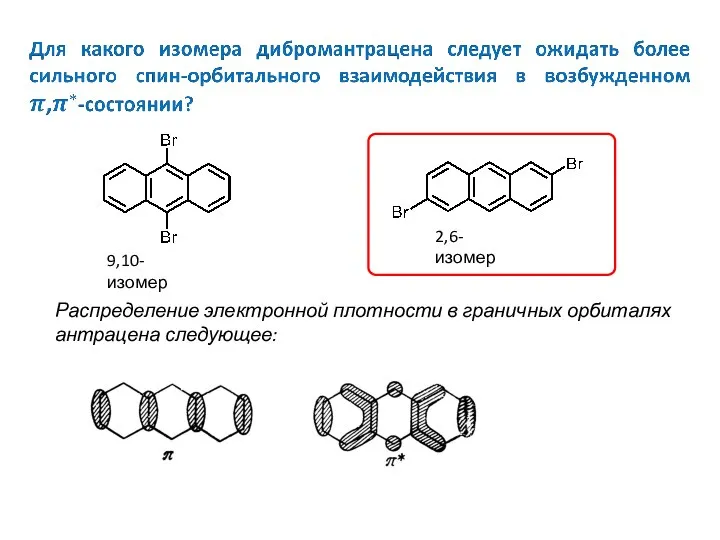
- 80. 9,10-изомер 2,6-изомер Распределение электронной плотности в граничных орбиталях антрацена следующее:
- 81. Электронный дипольный момент перехода Отбор по симметрии Отбор по перекрыванию Отбор по спину
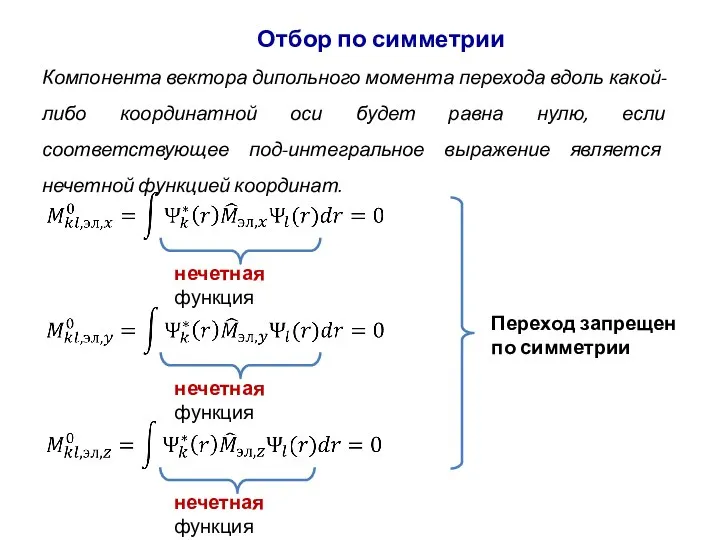
- 84. Отбор по симметрии Компонента вектора дипольного момента перехода вдоль какой-либо координатной оси будет равна нулю, если
- 85. Приближение Борна-Оппенгеймера (Б-О) выполняется, то есть: Снятие запрета по симметрии Отбор по симметрии Отбор по перекрыванию
- 86. Вибронное взаимодействие Вибронным взаимодействием называют смешивание электронных состояний вследствие взаимосвязи движения ядер молекулы с движением электронов.
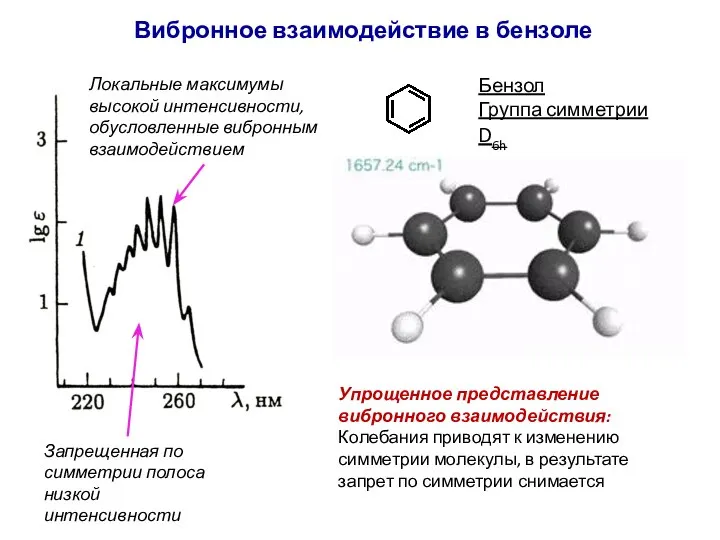
- 87. Вибронное взаимодействие в бензоле Бензол Группа симметрии D6h Запрещенная по симметрии полоса низкой интенсивности Локальные максимумы
- 89. Скачать презентацию










































 Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения Физика со смешариками
Физика со смешариками Роль звуковых колебаний в окружающем мире
Роль звуковых колебаний в окружающем мире Изменение изотопного состава. Выгорание топлива
Изменение изотопного состава. Выгорание топлива Дефект массы
Дефект массы Сокращение времени проектирования движительно-рулевых колонок и подруливающих устройств в ЦПС
Сокращение времени проектирования движительно-рулевых колонок и подруливающих устройств в ЦПС Двигатель внутреннего сгорания
Двигатель внутреннего сгорания Работа и энергия
Работа и энергия Модели атомов. Опыты Резерфорда
Модели атомов. Опыты Резерфорда Кинематика материальной точки
Кинематика материальной точки Взаимодействие ионизирующего излучения с веществом
Взаимодействие ионизирующего излучения с веществом Решение задач на расчет полного сопротивления цепи
Решение задач на расчет полного сопротивления цепи Полупроводники. Собственная проводимость полупроводников
Полупроводники. Собственная проводимость полупроводников Скорость. Равномерное прямолинейное движение
Скорость. Равномерное прямолинейное движение Метрология. Случайные погрешности: статистические методы оценивания
Метрология. Случайные погрешности: статистические методы оценивания Мощность. Единицы мощности
Мощность. Единицы мощности Secret Portkey
Secret Portkey Повторение физики за 8 класс. Тест
Повторение физики за 8 класс. Тест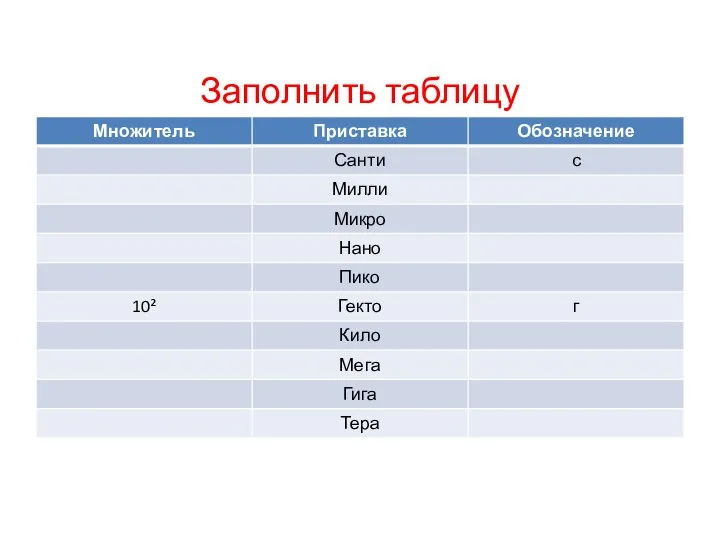 Технические измерения
Технические измерения Сила трения. Сила упругости
Сила трения. Сила упругости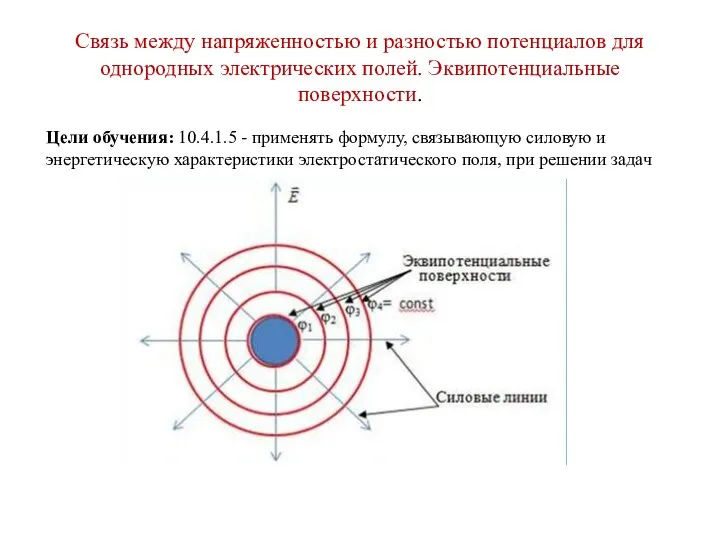 Эквипотенциальные поверхности
Эквипотенциальные поверхности Поршневой компрессор. Лабораторная работа
Поршневой компрессор. Лабораторная работа Основные физические явления, используемые в работе ТСО. Тема 3
Основные физические явления, используемые в работе ТСО. Тема 3 Самостоятельная работа 66 урок
Самостоятельная работа 66 урок Подход Лагранжа
Подход Лагранжа Динамика движения материальной точки по окружности. Тяготение
Динамика движения материальной точки по окружности. Тяготение Гидравлический домкрат в быту
Гидравлический домкрат в быту Тонкослойная хроматография
Тонкослойная хроматография