Содержание
Слайд 2Теорема о трех силах – Если тело, под действием трех непараллельных сил
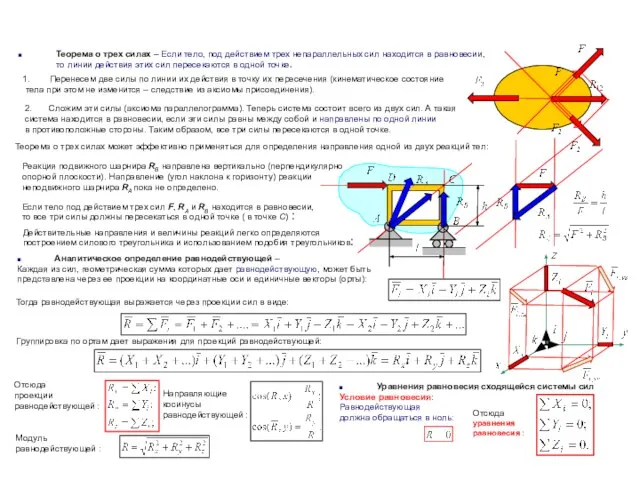
то линии действия этих сил пересекаются в одной точке.
Перенесем две силы по линии их действия в точку их пересечения (кинематическое состояние
тела при этом не изменится – следствие из аксиомы присоединения).
2. Сложим эти силы (аксиома параллелограмма). Теперь система состоит всего из двух сил. А такая
система находится в равновесии, если эти силы равны между собой и направлены по одной линии
в противоположные стороны. Таким образом, все три силы пересекаются в одной точке.
Теорема о трех силах может эффективно применяться для определения направления одной из двух реакций тел:
Реакция подвижного шарнира RB направлена вертикально (перпендикулярно
опорной плоскости). Направление (угол наклона к горизонту) реакции
неподвижного шарнира RA пока не определено.
Если тело под действием трех сил F, RA и RB находится в равновесии,
то все три силы должны пересекаться в одной точке ( в точке С) :
Действительные направления и величины реакций легко определяются
построением силового треугольника и использованием подобия треугольников:
Аналитическое определение равнодействующей –
Каждая из сил, геометрическая сумма которых дает равнодействующую, может быть
представлена через ее проекции на координатные оси и единичные векторы (орты):
Тогда равнодействующая выражается через проекции сил в виде:
Группировка по ортам дает выражения для проекций равнодействующей:
Отсюда
проекции
равнодействующей :
Модуль
равнодействующей :
Направляющие
косинусы
равнодействующей :
Уравнения равновесия сходящейся системы сил
Условие равновесия:
Равнодействующая
должна обращаться в ноль:
Отсюда
уравнения
равновесия :
Слайд 3Задача 1
Задача 1

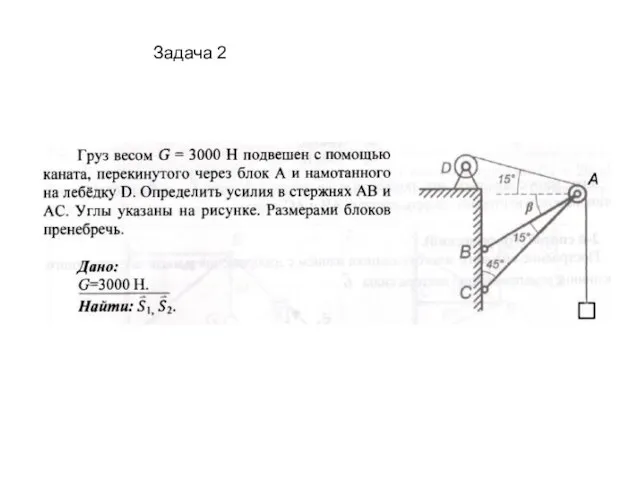
Слайд 4Задача 2
Задача 2
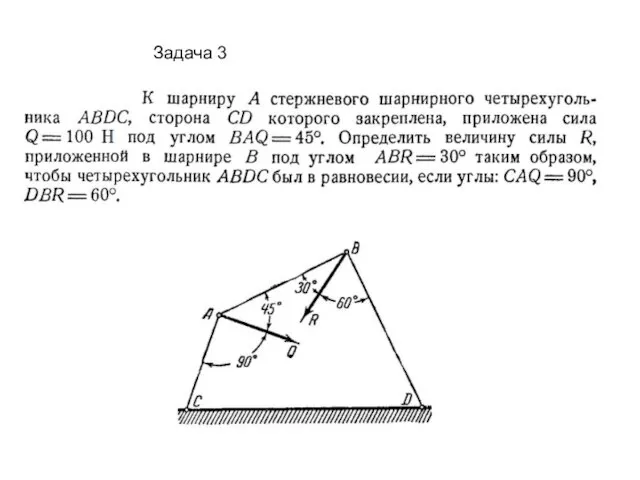
Слайд 5Задача 3
Задача 3
 Растяжение и сжатие
Растяжение и сжатие Порівняння роботи рухомого складу за різними видами тяги
Порівняння роботи рухомого складу за різними видами тяги Презентация на тему Электронно-лучевая трубка (10 класс)
Презентация на тему Электронно-лучевая трубка (10 класс)  Методическое пособие Мотошины, Колеса Даром
Методическое пособие Мотошины, Колеса Даром Электромагнитное излучение
Электромагнитное излучение Спор Альберта Эйнштейна и Нильса Бора
Спор Альберта Эйнштейна и Нильса Бора Теоретические основы электротехники. Трехфазные электрические цепи
Теоретические основы электротехники. Трехфазные электрические цепи Активация в ядерной физике. (Тема 2.8)
Активация в ядерной физике. (Тема 2.8) Импульс. Закон сохранения импульса
Импульс. Закон сохранения импульса Теплоносители и их свойства. Реальные газы. Уравнения состояний. Тройная точка воды. (Тема 5)
Теплоносители и их свойства. Реальные газы. Уравнения состояний. Тройная точка воды. (Тема 5) Фотоны. Период формирования
Фотоны. Период формирования Тритий
Тритий Применение электромагнитной индукции
Применение электромагнитной индукции Ядерный (атомный) реактор
Ядерный (атомный) реактор Презентация на тему Плотность тела
Презентация на тему Плотность тела  Кинематика_ _Лекция 1_ (1)
Кинематика_ _Лекция 1_ (1) Качественные методы исследования нелинейных систем. Устойчивость положения равновесия динамических систем
Качественные методы исследования нелинейных систем. Устойчивость положения равновесия динамических систем Динамика
Динамика Графит и алмаз. Кристаллы
Графит и алмаз. Кристаллы Оптика. Лекция 3.2
Оптика. Лекция 3.2 Верификация на Нововоронежской АЭС акустической модели реактора ВВЭР
Верификация на Нововоронежской АЭС акустической модели реактора ВВЭР Нагревание проводников электрическим током. Закон Джоуля-Ленца
Нагревание проводников электрическим током. Закон Джоуля-Ленца ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР
ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР Погрешности измерения. 7 класс
Погрешности измерения. 7 класс Закон сохранения момента импульса
Закон сохранения момента импульса Устройство механической коробки передач
Устройство механической коробки передач Задание по физике в формате ОГЭ
Задание по физике в формате ОГЭ Использование электромагнитов
Использование электромагнитов