Складний опір. Тема 1.8

2
1. Загальний випадок навантаження стержня. Внутрішні сили і напруження
Рис. 1
Розглянемо прямий стержень, який навантажений зрівноваженою системою зовнішніх сил (рис. 1, а). На підставі методу перерізів для визначення внутрішніх сил встановлено, що загалом у перерізі можуть виникати: повздовжня сила, поперечні сили, крутний момент та згинальні моменти (рис. 1, б). Для визначення цих шести внутрішніх сил складають для частини стержня, яку розглядають, шість рівнянь статики (табл. 1). Із кожною з внутрішніх сил пов’язані напруження, які визначають за формулами табл. 1.
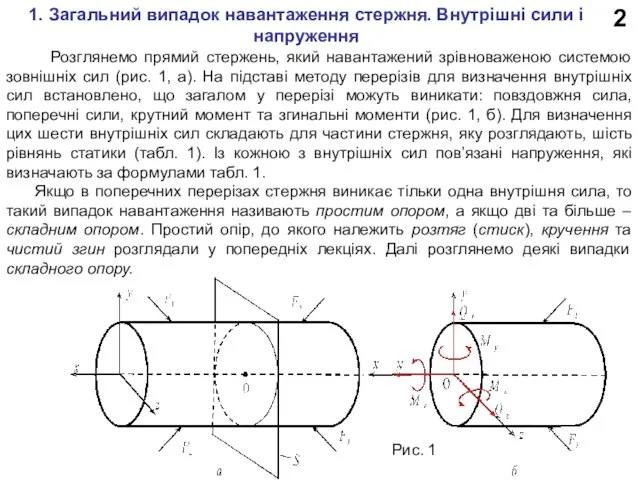
Якщо в поперечних перерізах стержня виникає тільки одна внутрішня сила, то такий випадок навантаження називають простим опором, а якщо дві та більше – складним опором. Простий опір, до якого належить розтяг (стиск), кручення та чистий згин розглядали у попередніх лекціях. Далі розглянемо деякі випадки складного опору.

2
Таблиця 1
Поперечна сила Q z
Згинальний момент My
Згинальний момент Mz

4
Випадки складного опору
1. Косий згин балки. У перерізах виникають моменти M y, M z та поперечні сили Q y, Q z. При розрахунках на міцність впливом поперечних сил найчастіше нехтують.
2. Позацентровий розтяг (стиск). У перерізах виникають: повздовжня сила N та згинальні моменти M y, M z .
3. Сумісний згин і кручення. У перерізах виникають крутний момент MK і згинальні моменти (або один з них) M y, M z .
За малих переміщень і деформацій стержнів напруження та деформації (переміщення) у разі складного опору визначають на основі принципу незалежності дії сил, як алгебраїчну суму відповідних напружень і геометричну суму деформацій, зумовлених кожною внутрішньою силою зокрема. Отже, в загальному випадку складного опору:
Якщо знехтувати малими дотичними напруженнями від поперечних сил, тоді

5
2. Косий згин
Рис. 2
Косий згин зумовлений навантаженням, рівнодійна якого проходить через центр поперечного перерізу під певним кутом до його головних центральних осей (рис. 2).
Навантаження можна розкласти на складові у напрямку осей y, z. Тому косий згин подають як суму двох прямих згинів – у вертикальній та горизонтальній площинах.
У довільному перерізі балки виникають згинальні моменти та поперечні сили. Напруження у довільній точці перерізу A (y, z) перерізу визначають, як суму напружень від згинальних моментів (1). Геометричне місце точок, в яких σ=0, називають нейтральною лінією. Це – пряма лінія, що проходить через центр ваги перерізу і нахилена до горизонтальної осі z під кутом α, який визначають зі співвідношення (2).

6
Максимальних значень нормальні напруження досягають в точках, найбільш віддалених від нейтральної лінії
Косий згин
або
Умова міцності при косому згині
При підборі розмірів перерізів використовують вираз
у якому відношення осьових моментів опору задають.

7
3. Позацентровий розтяг (стиск) стержня великої жорсткості
Позацентровий розтяг (стиск) зумовлений навантаженням, рівнодійна якого F паралельна до осі стержня (рис. 3, а) та прикладена в точці з координатами
У цьому випадку в перерізах стержня виникають поздовжня сила та згинальні моменти. Нормальне напруження в точці B (y, z) перерізу визначають за залежністю (5):
Рис. 3
де квадрати радіусів інерції перерізу:
У формулі (6) за позацентрового розтягу залишають знак “+“, за стиску – знак “– “.

8
Лінію, на якій нормальні напруження дорівнюють нулю, називають нейтральною лінією. Це – пряма лінія (рис. 3, б), що відсікає на осях відрізки:
Позацентровий розтяг (стиск)
Залежно від координат точки прикладання сили F нейтральна лінія може проходити поза перерізом, дотикатися до нього або перетинати його. В останньому випадку в перерізі виникають напруження і розтягу, і стиску. Найбільшого значення напруження набувають у точках, що розміщені якнайдалі від нейтральної лінії.
Для стиснутих позацентрово стержнів, виготовлених з крихких матеріалів, небажана поява в точках перерізу напружень розтягу, оскільки тоді можливе виникнення тріщин. Для уникнення цих напружень, позацентрову силу слід прикладати в межах ядра перерізу. Ядро перерізу – це область довкола центра ваги перерізу, в якій всяка позацентрово прикладена сила породжує по всьому перерізі напруження того ж знаку, що і прикладена сила. Координати точок контуру ядра перерізу визначають з умов
де відстані, що відтинає нейтральна лінія на осях (рис. 3, б), коли ця лінія дотикається до контуру поперечного перерізу стержня. Умови міцності для матеріалу, що неоднаково працює на розтяг і стиск :

9
4. Сумісний згин з крученням
Рис. 4
Сумісний згин з крученням має місце тоді, коли в стержні виникають водночас згинальні і крутний момент. З наявністю цих моментів пов’язані напруження нормальні та дотичні напруження. Матеріал стержня перебуває у плоскому напруженому стані (рис. 4, а) з головними напруженнями
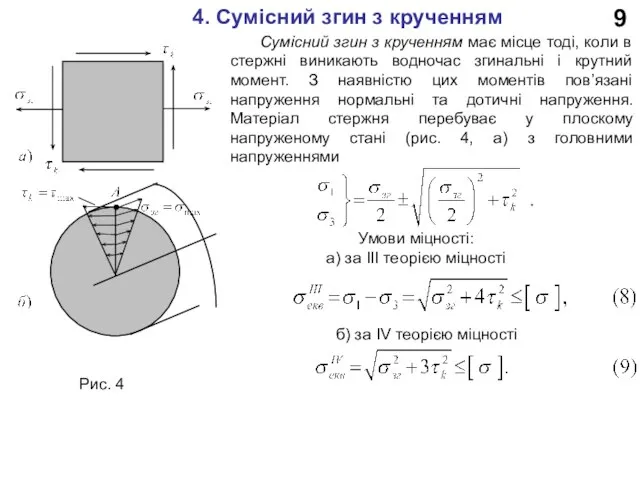
Умови міцності:
а) за III теорією міцності
б) за IV теорією міцності