Стандартная атмосфера. Лекция 4

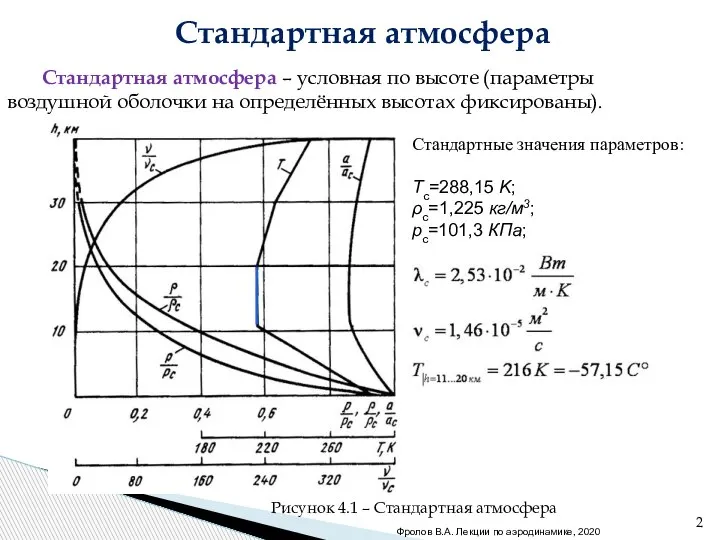
Стандартная атмосфера
.
Стандартная атмосфера – условная по высоте (параметры воздушной оболочки на определённых высотах фиксированы).
Стандартные значения параметров:
Tc=288,15 K;
ρc=1,225 кг/м3;
pc=101,3 КПа;
Фролов В.А. Лекции по аэродинамике, 2020
Рисунок 4.1 – Стандартная атмосфера

Кинематика жидкости. Ускорение
Кинематика жидкости – раздел механики, который рассматривает поле скорости, ускорения и не рассматривает силовое воздействие между телом и средой.
(4.1)
(4.2)
(4.3)
(4.4)
Фролов В.А. Лекции по аэродинамике, 2020

Кинематика жидкости. Ускорение
.
Скалярное произведение двух векторов:
- локальное (субстанциональное) ускорение
- конвективное ускорение
(4.5)
(4.6)
(4.7)
(4.8)
Фролов В.А. Лекции по аэродинамике, 2020

Кинематика жидкости. Частные производные
(4.9)
(4.10)
(4.11)
(4.12)
(4.13)
(4.14)
(4.15)
(4.16)
Фролов В.А. Лекции по аэродинамике, 2020

Частные производные температуры, энтальпии и энтропии
(4.17)
Фролов В.А. Лекции по аэродинамике, 2020

Линия тока
.
Рисунок 4.2 – Линия тока
Кривая в пространстве, в каждой точке которой в данный момент времени вектор скорости совпадает с касательной в этой точке называется линией тока.
Фролов В.А. Лекции по аэродинамике, 2020

Фролов В.А. Лекции по аэродинамике, 2020
Дифференциальное уравнение линии тока

Дифференциальное уравнение линии тока:
Траектория это след частицы в пространстве.
Если рассматривать установившееся (стационарное) течение, линия тока и траектория совпадают. Обратное не выполняется.
Уравнение линии тока и траектории
Система дифференциальных уравнений траектории:
(4.18)
(4.19)
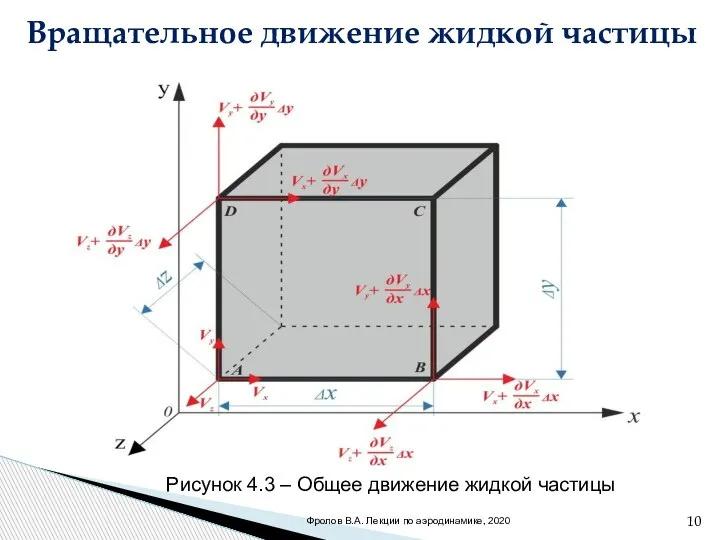
Фролов В.А. Лекции по аэродинамике, 2020

Вращательное движение жидкой частицы
.
Рисунок 4.3 – Общее движение жидкой частицы
Фролов В.А. Лекции по аэродинамике, 2020

Вращательное движение жидкой частицы
.
Будем полагать вектор скорости непрерывной функцией координат и времени.
Непрерывная функция является дифференцируемой функцией.
Дифференцируемая функцией может быть разложена в ряд Тейлора.
Фролов В.А. Лекции по аэродинамике, 2020

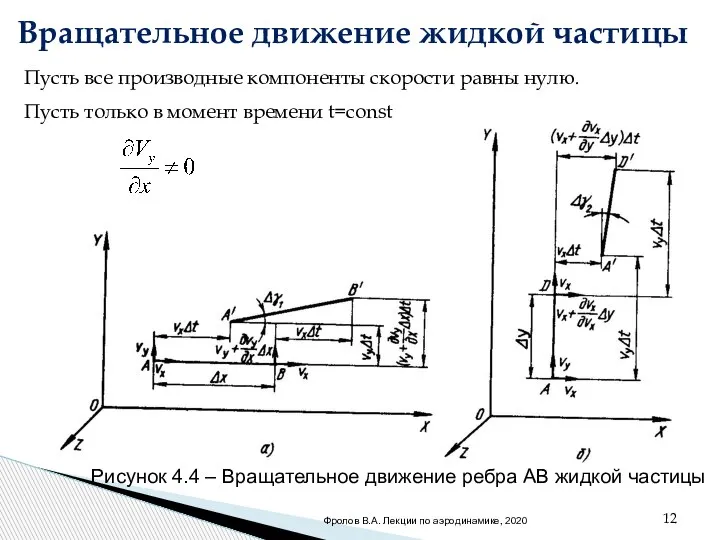
Вращательное движение жидкой частицы
.
Пусть все производные компоненты скорости равны нулю.
Пусть только в момент времени t=const
Рисунок 4.4 – Вращательное движение ребра АВ жидкой частицы
Фролов В.А. Лекции по аэродинамике, 2020

.
(4.20)
(4.21)
(4.22)
Вращательное движение жидкой частицы
Фролов В.А. Лекции по аэродинамике, 2020
Правило знаков: вращение против часовой стрелки «+», а по часовой – «-»

.
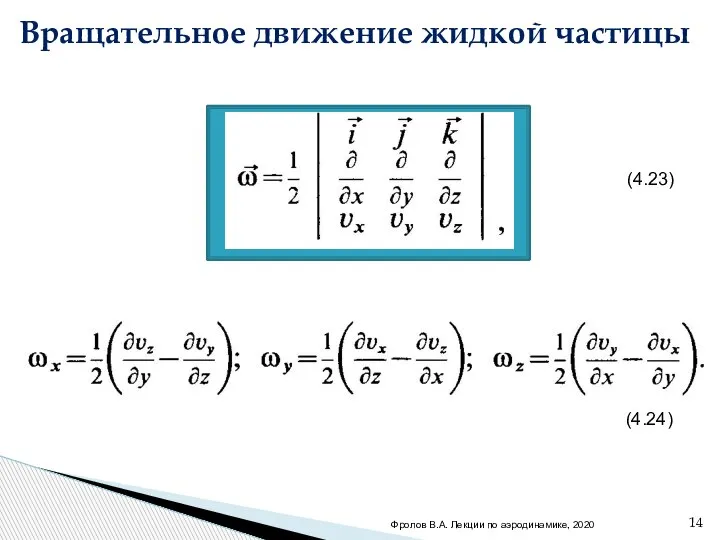
(4.23)
(4.24)
Вращательное движение жидкой частицы
Фролов В.А. Лекции по аэродинамике, 2020

Деформационное движение жидкой частицы
.
Рисунок 4.5 – Деформационное движение ребра АВ жидкой частицы
(4.25)
(4.26)
(4.27)
Фролов В.А. Лекции по аэродинамике, 2020

Деформация скашивания при движении жидкой частицы
.
Тензор скоростей деформаций
(4.28)
(4.29)
(4.30)
Фролов В.А. Лекции по аэродинамике, 2020

Уравнение неразрывности
.
Относительное изменение объёма по времени равно
(4.31)
(4.32)
(4.33)
(4.34)
(4.35)
Фролов В.А. Лекции по аэродинамике, 2020

Уравнение неразрывности
.
(4.36)
(4.37)
Фролов В.А. Лекции по аэродинамике, 2020