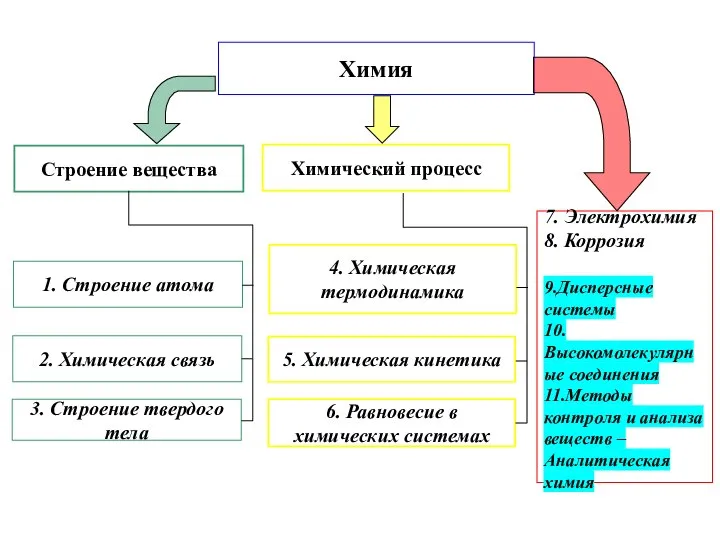
Содержание
- 2. Химия 1. Строение атома 2. Химическая связь 3. Строение твердого тела 4. Химическая термодинамика 5. Химическая
- 4. I. Строение атома 3 этапа развития учения о строении атома 1 – Натурфилософские представления об атомном
- 5. Физические модели строения атома Эрнест Резерфорд - планетарная модель атома (1911 г.) Атом - сложная частица,
- 6. Корпускулярно-волновой дуализм свойств материи [проблема природы лучистой энергии - эл.магн.излучения(ЭМИ)] Электромагнитное излучение Волна: λ - длина
- 7. (дуализм-общее свойство материи, а не только ЭМИ) - гипотеза-постулат о связи импульса P любого движущегося материальн.объекта
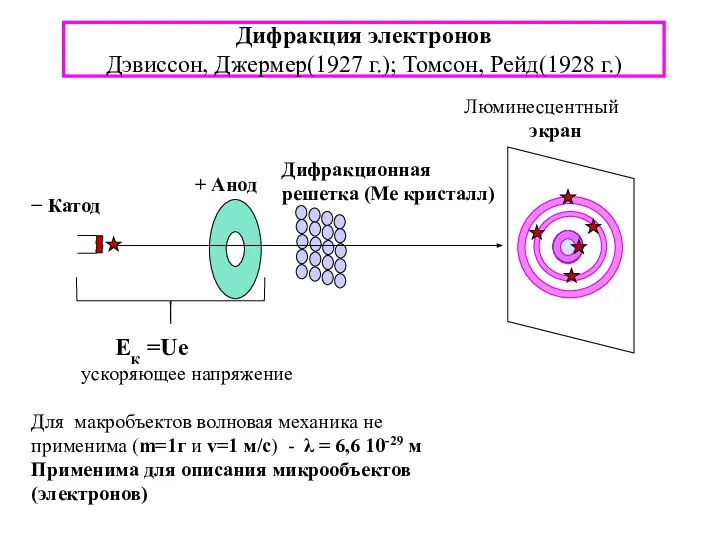
- 8. Дифракция электронов Дэвиссон, Джермер(1927 г.); Томсон, Рейд(1928 г.) + Анод
- 9. Принцип неопределенности [для микрочастиц(электрона)] Вернер Гейзенберг постулировал этот принцип в 1927 г. для одномерного пространства в
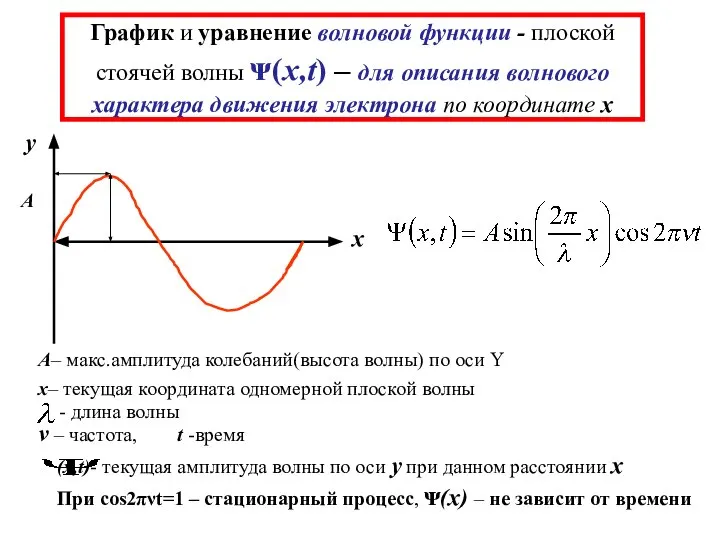
- 10. График и уравнение волновой функции - плоской стоячей волны ᴪ(x,t) – для описания волнового характера движения
- 11. Уравнение Шредингера 1. Уравнение отображает волновой характер движения электрона в 3-х мерном пространстве с координатами (x,y,z)
- 12. λ → m, Ek = mv 2 / 2 = m 2 v 2 / 2m
- 13. Физический смысл волновой функции Ψ(x,y,z) - пси функция - волновая функция Макс Борн, 1926 г. волновая
- 14. Электрон в одномерном потенциальном ящике(яме). Решение ур. Шредингера. Потенциальная яма (ящик) - область пространства, вне которой
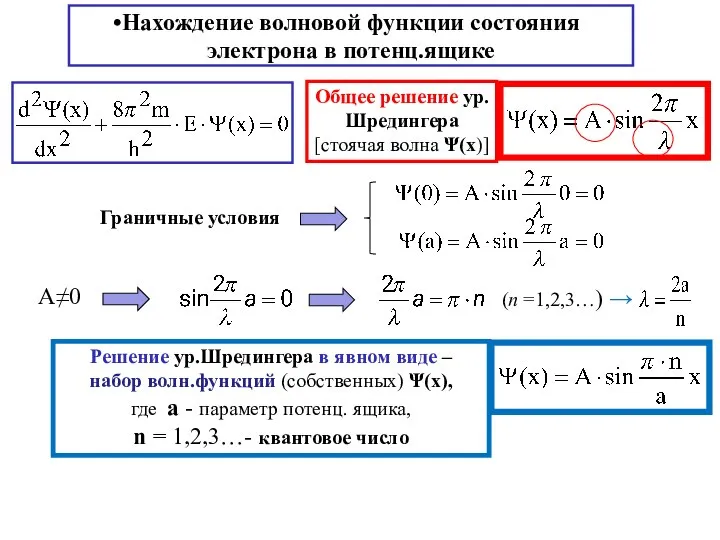
- 15. Нахождение волновой функции состояния электрона в потенц.ящике Решение ур.Шредингера в явном виде – набор волн.функций (собственных)
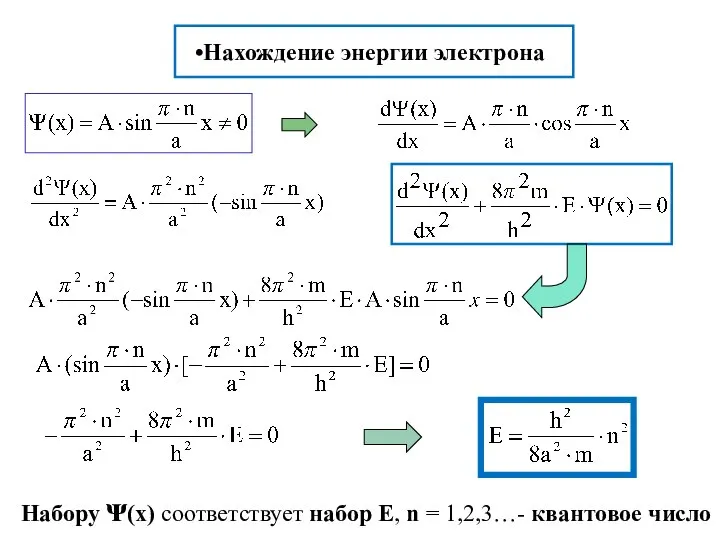
- 16. Нахождение энергии электрона Набору ᴪ(x) соответствует набор Е, n = 1,2,3…- квантовое число
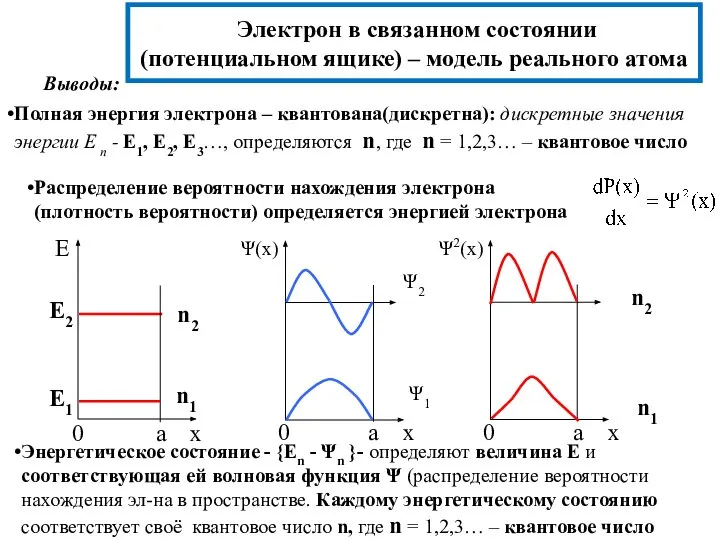
- 17. Электрон в связанном состоянии (потенциальном ящике) – модель реального атома Выводы: Полная энергия электрона – квантована(дискретна):
- 18. Электрон в трехмерном потенциальном ящике Решение: электрон описывается где a,b,c – параметры потенц.ящика; nx, ny, nz(1,2,3,4…
- 19. Вырожденные энергетические состояния Одно значение энергии – при нескольких наборах квантовых чисел (несколько наборов волновых функций).
- 20. Квантово-механическая модель атома. Основное состояние атома водорода [k=1/4πε0] - константа в з-не Кулона x = r⋅sinϑ⋅cosϕ
- 21. Решение уравнения Шредингера для основного состояния атома водорода
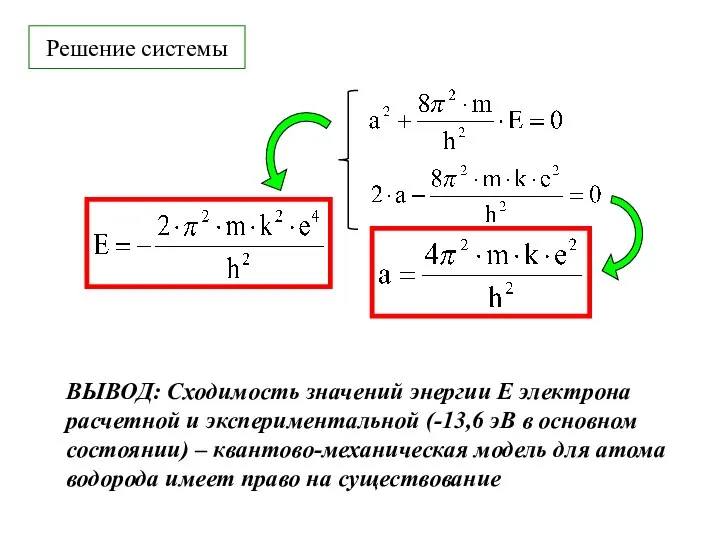
- 22. Решение системы ВЫВОД: Сходимость значений энергии Е электрона расчетной и экспериментальной (-13,6 эВ в основном состоянии)
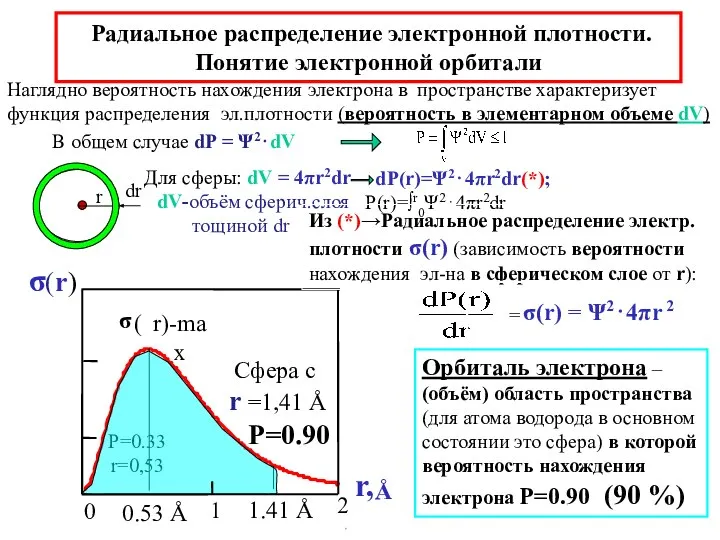
- 23. Радиальное распределение электронной плотности. Понятие электронной орбитали 1.41 Å Для сферы: dV = 4πr2dr dV-объём сферич.слоя
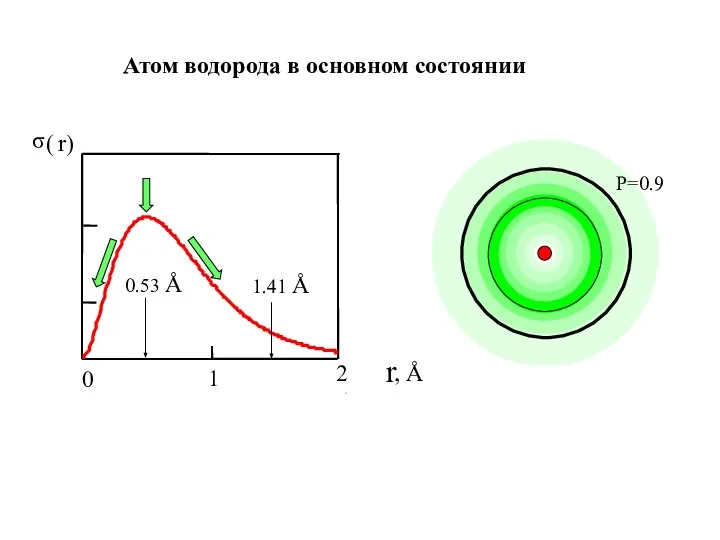
- 24. Атом водорода в основном состоянии
- 25. Возбужденные состояния атома водорода –более сложный вид волновых функций, чем Ψ(r) Общий вид таких волновых функций
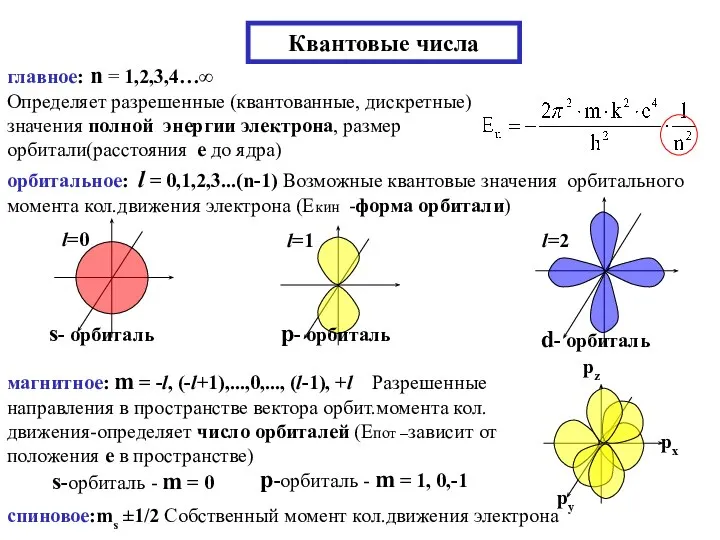
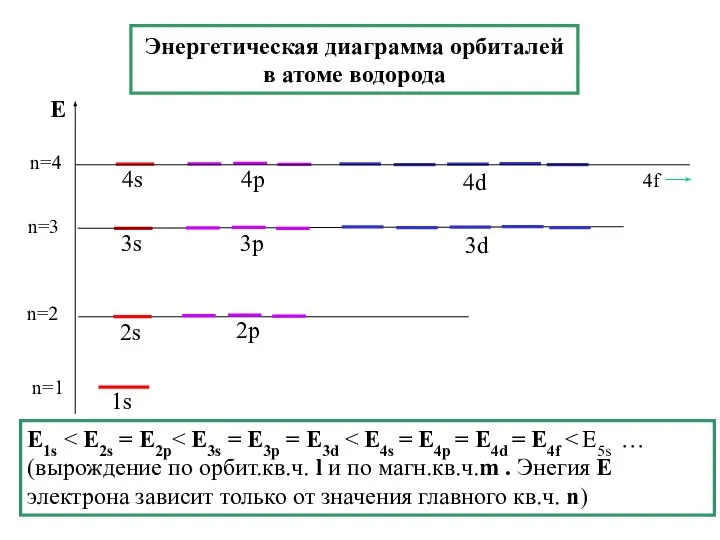
- 26. Квантовые числа главное: n = 1,2,3,4…∞ Определяет разрешенные (квантованные, дискретные) значения полной энергии электрона, размер орбитали(расстояния
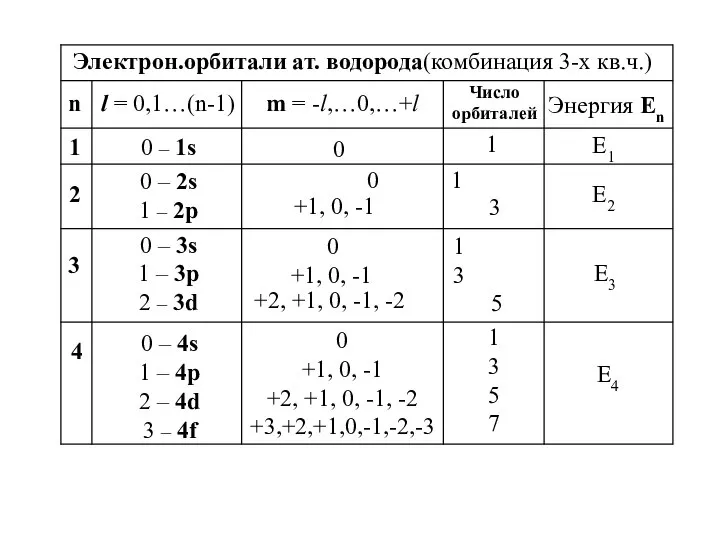
- 27. n l = 0,1…(n-1) m = -l,…0,…+l Число орбиталей Энергия Еn 1 E2 2 1 0
- 28. Энергетическая диаграмма орбиталей в атоме водорода n=1 E1s
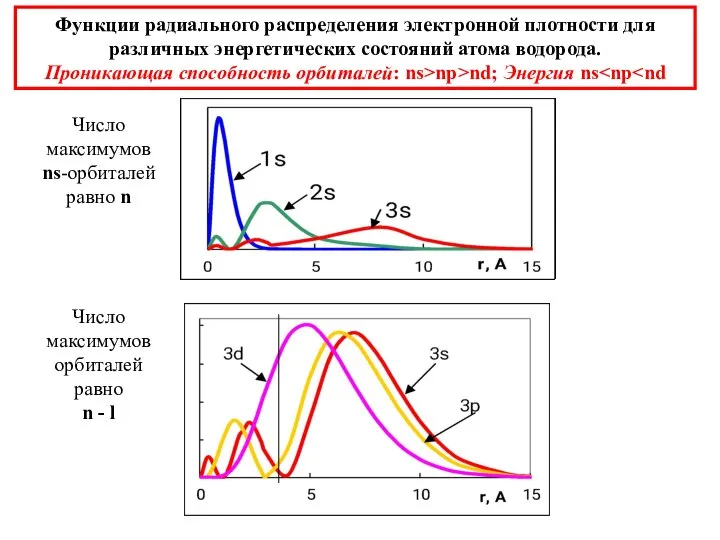
- 29. Функции радиального распределения электронной плотности для различных энергетических состояний атома водорода. Проникающая способность орбиталей: ns>np>nd; Энергия
- 30. 1.7 Многоэлектронный атом (одноэлектронное приближение - водородоподобная система, описание многоэлектронного атома похоже на описание атома водорода).
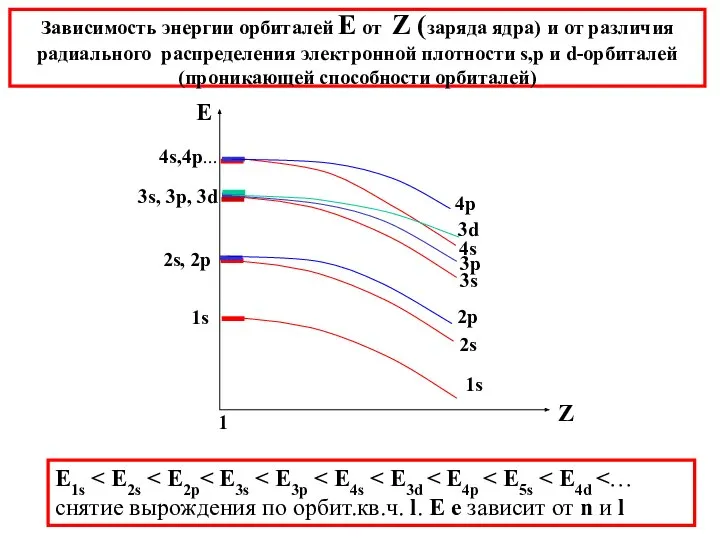
- 31. Зависимость энергии орбиталей Е от Z (заряда ядра) и от различия радиального распределения электронной плотности s,p
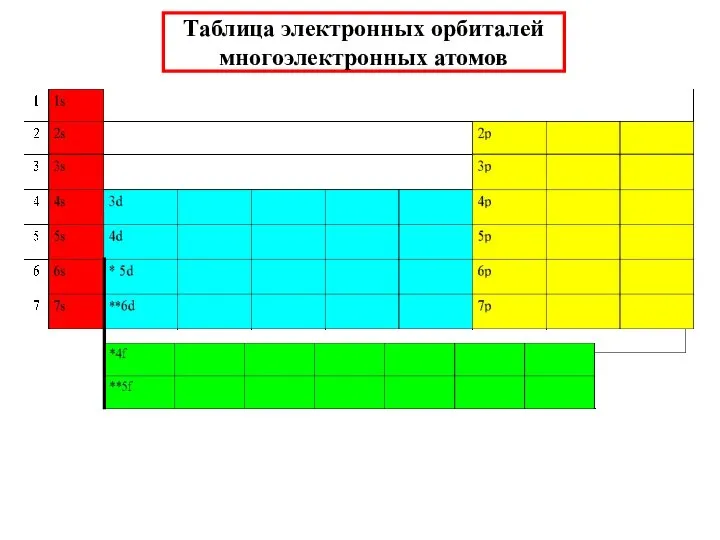
- 32. Таблица электронных орбиталей многоэлектронных атомов
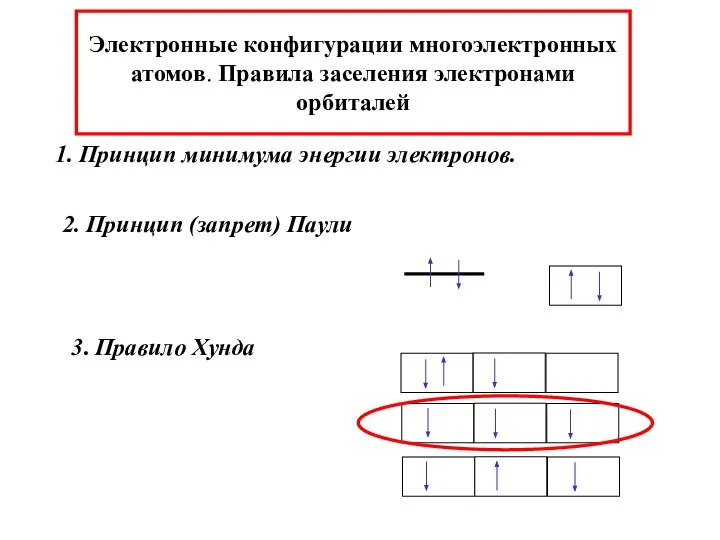
- 33. Электронные конфигурации многоэлектронных атомов. Правила заселения электронами орбиталей 1. Принцип минимума энергии электронов. 2. Принцип (запрет)
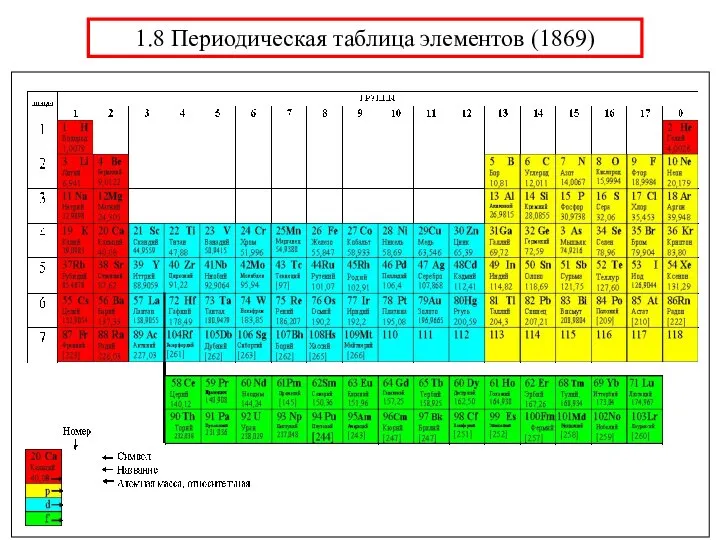
- 34. 1.8 Периодическая таблица элементов (1869)
- 35. Физико-химические характеристики атома Ковалентный радиус ( RA = rсв /2) и радиус иона
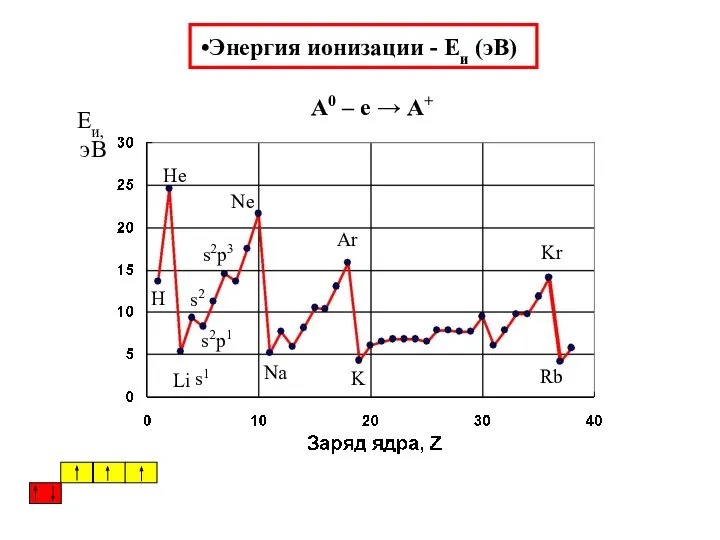
- 36. Энергия ионизации - Eи (эВ) А0 – е → А+ s1 s2 s2p1 s2p3
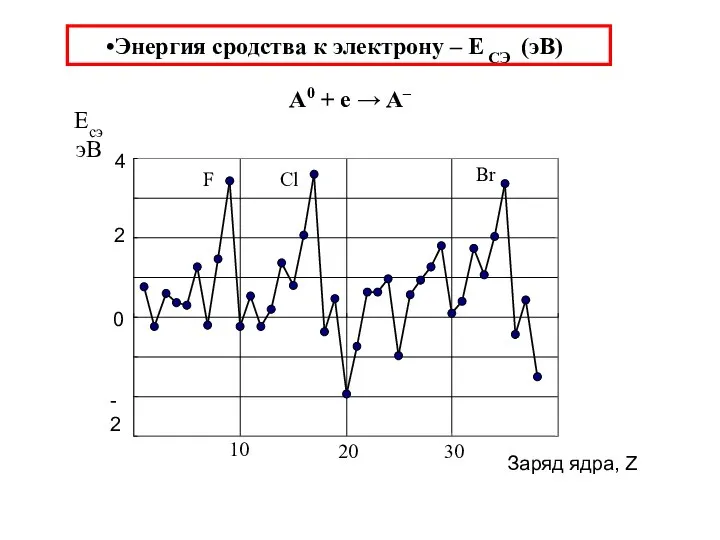
- 37. Энергия сродства к электрону – Е СЭ (эВ) A0 + e → A–
- 39. Скачать презентацию


![Корпускулярно-волновой дуализм свойств материи [проблема природы лучистой энергии - эл.магн.излучения(ЭМИ)] Электромагнитное излучение](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959820/slide-5.jpg)

![Принцип неопределенности [для микрочастиц(электрона)] Вернер Гейзенберг постулировал этот принцип в 1927 г.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959820/slide-8.jpg)






![Квантово-механическая модель атома. Основное состояние атома водорода [k=1/4πε0] - константа в з-не](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959820/slide-19.jpg)




 Электрокинетические явления
Электрокинетические явления Теоретический чертеж. Координатные оси
Теоретический чертеж. Координатные оси Основные понятия, определения и законы электромеханики
Основные понятия, определения и законы электромеханики Телескопи. Типи телескопів за розташуванням
Телескопи. Типи телескопів за розташуванням M_P_Rezistivnye_M (1)
M_P_Rezistivnye_M (1) Презентация Механика Лекция 1
Презентация Механика Лекция 1 Резистор. Функциональное назначение резистра
Резистор. Функциональное назначение резистра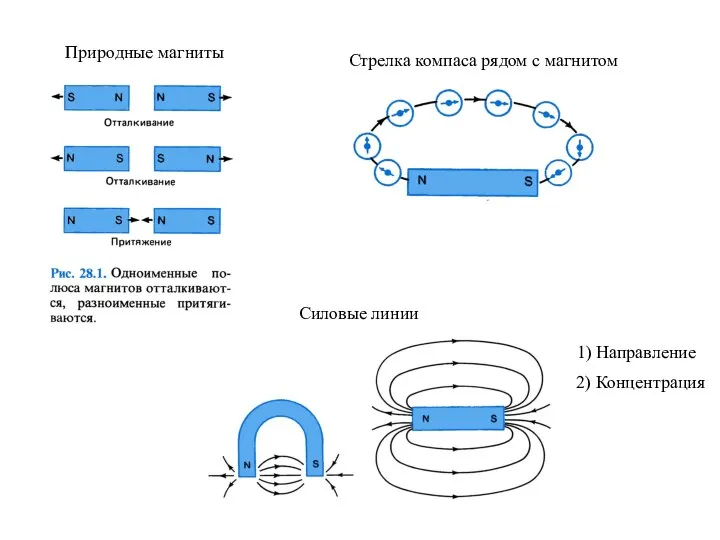 Природные магниты
Природные магниты L2_1_Mekhanicheskie_kharakteristiki_metallov
L2_1_Mekhanicheskie_kharakteristiki_metallov Реостаты
Реостаты Оптимизация методики разделения лечебного препарата Clopidogrel Hydrogen Sulfate с сопутствующей примесью (А)
Оптимизация методики разделения лечебного препарата Clopidogrel Hydrogen Sulfate с сопутствующей примесью (А) Интерактивная игра по физике Эрудит. Для учащихся 7 класса
Интерактивная игра по физике Эрудит. Для учащихся 7 класса Изменения агрегатных состояний вещества. Физический диктант
Изменения агрегатных состояний вещества. Физический диктант Решение задач на расчёт КПД теплового двигателя. 8 класс
Решение задач на расчёт КПД теплового двигателя. 8 класс Методы обзора пространства и измерения координат
Методы обзора пространства и измерения координат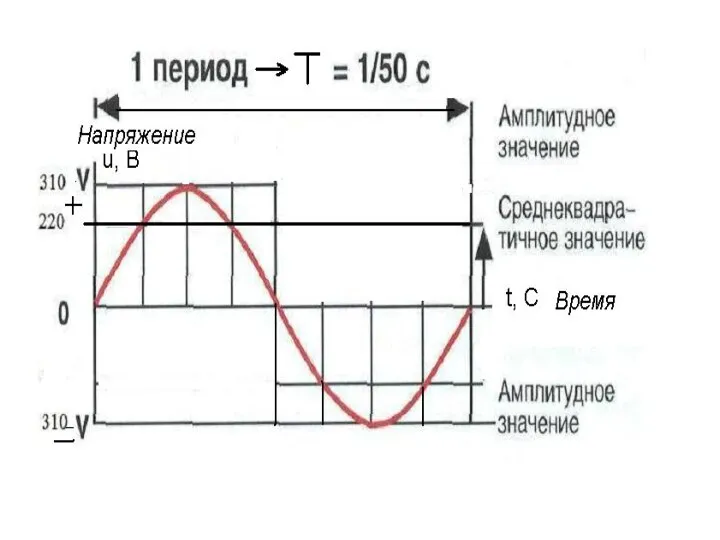 Действующее и среднее значение синусоидального тока
Действующее и среднее значение синусоидального тока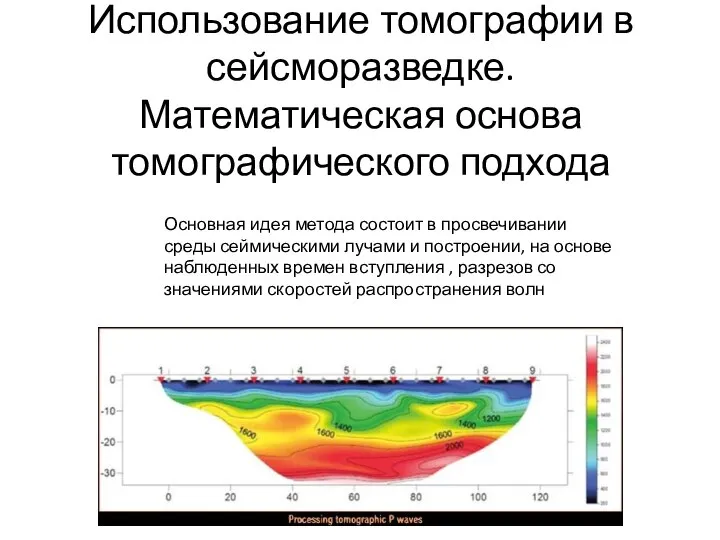 Использование томографии в сейсморазведке. Математическая основа томографического подхода
Использование томографии в сейсморазведке. Математическая основа томографического подхода Закон Ома для участка цепи
Закон Ома для участка цепи Давление газа
Давление газа Основные положения технической термодинамики
Основные положения технической термодинамики Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю
Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю Физика на рыбалке
Физика на рыбалке Инерция в жизни человека
Инерция в жизни человека Движение жидкостей и газов. Закон Бернулли
Движение жидкостей и газов. Закон Бернулли Динамика. Законы механики Ньютона
Динамика. Законы механики Ньютона Переменный ток
Переменный ток В мире звуков
В мире звуков Реактивное движение
Реактивное движение