Теорема Гаусса-Остроградского. Поток вектора напряжённости электростатического поля. Электрические поля

Карл Фридрих Гаусс (1777-1855) — немецкий математик, астроном, геодезист и физик. Считается одним из величайших математиков всех времён, «королём математиков». Лауреат медали Копли (1838), иностранный член Шведской (1821) и Российской (1824) Академий наук, английского Королевского общества.
Карл Гаусс родился 30 апреля 1777 года в Брауншвейге, ныне Германия. Еще при жизни он был удостоен почетного титула «принц математиков». Он был единственным сыном бедных родителей. Школьные учителя были так поражены его математическими и лингвистическими способностями, что обратились к герцогу Брауншвейгскому с просьбой о поддержке, и герцог дал деньги на продолжение обучения в школе и в Геттингенском университете (в 1795-98). Степень доктора Гаусс получил в 1799 в университете Хельмштедта.

Закон Кулона- основной закон электростатики.
Из него следует основная теорема электростатики – теорема Гаусса.
Введем новую величину – поток напряженности электрического поля. Выбираем в поле элемент площадью ∆S такой малый, чтобы напряженность поля была во всех точках одинакова.

Расчёт электрических полей значительно упрощается если использовать теорему Гаусса, определяющую поток вектора напряжённости электрического поля.

ΔΦ = EΔS cos α = EnΔS
Φ - поток вектора напряженности электрического поля.
Теорема Гаусса для вектора напряжённости.

Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля
через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
Внимание! Знак ∑ - означает сумму!

Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать
Задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R.
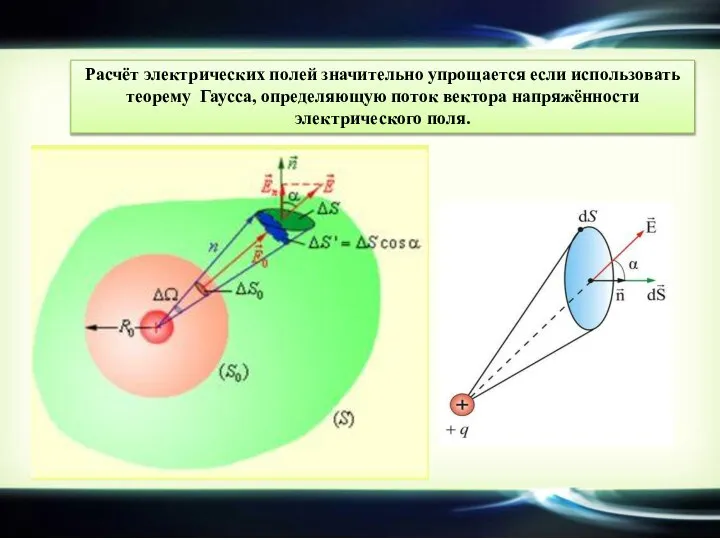
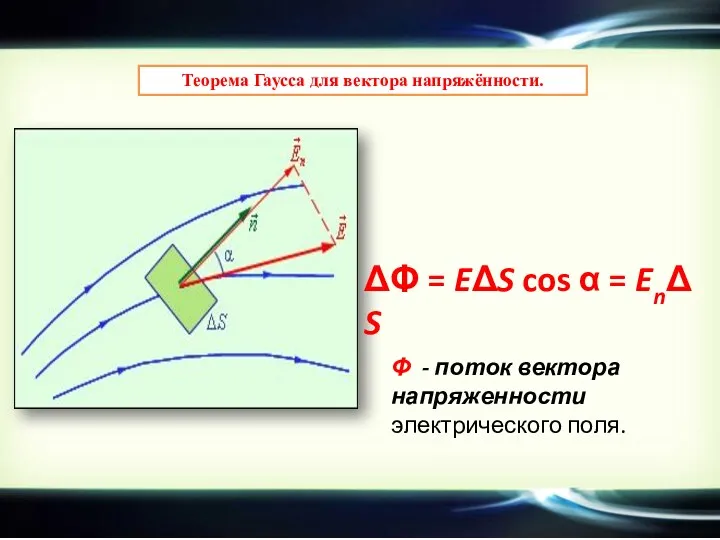
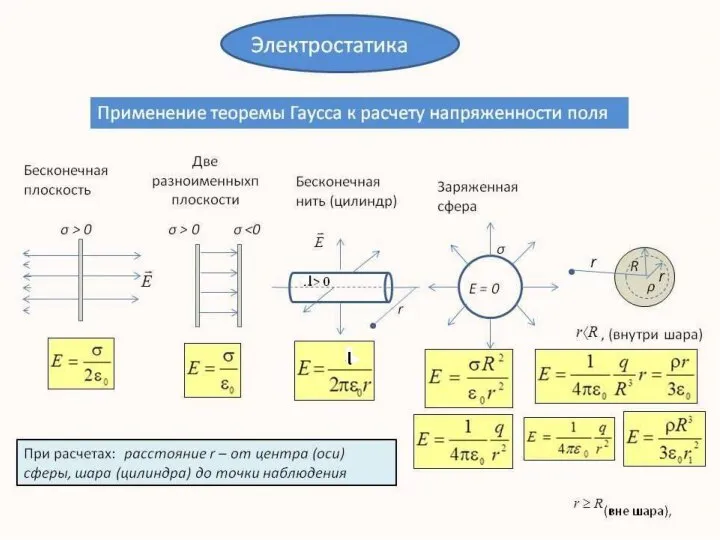
Эта задача имеет осевую симметрию. Из соображений симметрии, электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов
При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю.
где τ – заряд единицы длины цилиндра. Отсюда