Классификация связей в динамике

Рассмотреть классификацию связей в динамике, познакомиться с принципом возможных перемещений и научиться с помощью этого принципа решать задачи статики.
ПЛАН ЛЕКЦИИ
Классификация связей;
Принцип возможных перемещений;
Решение задач;
Заключение.
ЦЕЛЬ ЛЕКЦИИ
2

В статике:
Связи - то, что не даёт перемещаться
Действие связей описывается реакциями.
В аналитической механике:
Связи - любого вида ограничения, которые налагаются на положение и скорость движущихся тел (точек).
Действие связи описывается уравнениями (или неравенствами), которые определяют ограничения на движение тел.
СВЯЗИ
Классификация связей

Односторонние (неудерживающие, освобождающие) - связи, которые задаются неравенством:
КЛАССИФИКАЦИЯ СВЯЗЕЙ
Классификация связей

Двусторонние (удерживающие, неосвобождающие) – связи, которые задаются уравнением:
КЛАССИФИКАЦИЯ СВЯЗЕЙ
Классификация связей

Стационарные связи - связи, уравнения которых не содержат времени в явном виде:
КЛАССИФИКАЦИЯ СВЯЗЕЙ
Классификация связей

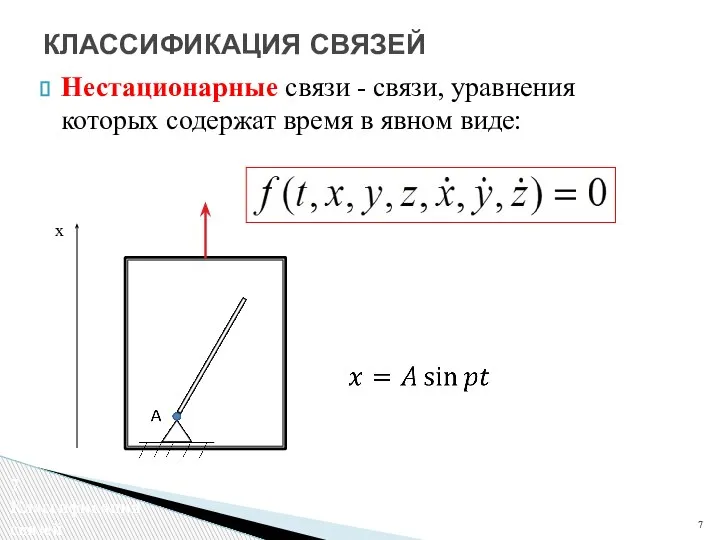
Нестационарные связи - связи, уравнения которых содержат время в явном виде:
КЛАССИФИКАЦИЯ СВЯЗЕЙ
x
Классификация связей

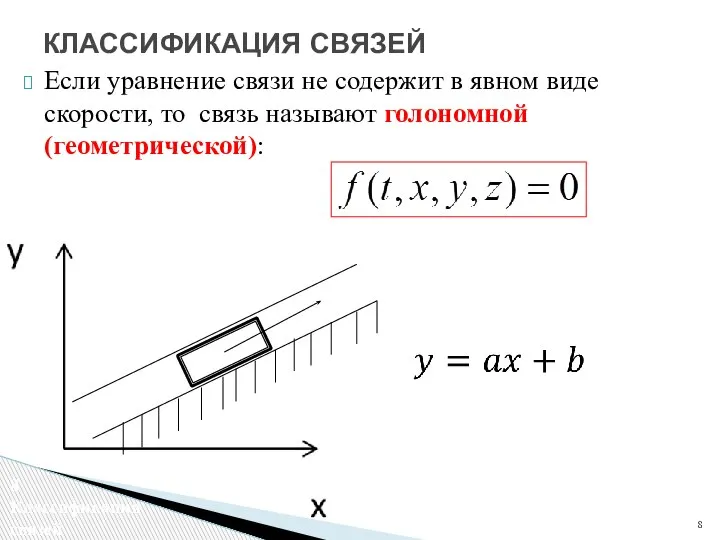
Если уравнение связи не содержит в явном виде скорости, то связь называют голономной (геометрической):
КЛАССИФИКАЦИЯ СВЯЗЕЙ
Классификация связей

Если уравнение связи содержит в явном виде скорость, то связь называют неголономной:
КЛАССИФИКАЦИЯ СВЯЗЕЙ
A
Классификация связей

ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Принцип
возможных перемещений

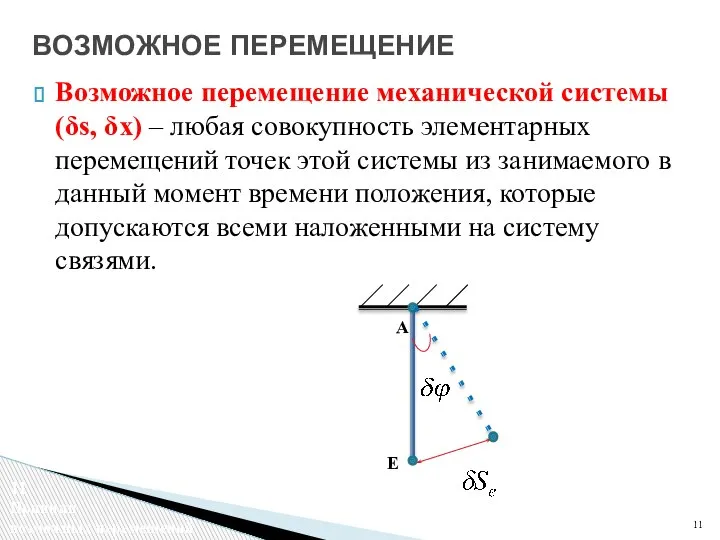
Возможное перемещение механической системы (δs, δx) – любая совокупность элементарных перемещений точек этой системы из занимаемого в данный момент времени положения, которые допускаются всеми наложенными на систему связями.
ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ
А
Е
Принцип
возможных перемещений

Возможные перемещения характеризуются тем, что они:
могут и не происходить (они воображаемые);
бесконечно малые;
происходят с сохранением всех наложенных на систему связей;
не связаны с реальным времененм (δt = 0).
Для стационарных связей действительное перемещение dr можно представить как набор возможных
ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ
Принцип
возможных перемещений

Возможная работа – это элементарная работа, которую действующая на материальную точку сила могла бы совершить на перемещении, совпадающем с возможным перемещением этой точки:
Связи, сумма возможных работ реакций которых на любом возможном перемещении равна нулю, называются идеальными связями :
ВОЗМОЖНАЯ РАБОТА
Принцип
возможных перемещений

Устанавливает общее условие равновесия механической системы в целом
При идеальных связях позволяет исключить из рассмотрения все неизвестные реакции связей
Выполняется в инерциальных системах отсчета
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Принцип
возможных перемещений

ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на неё активных сил при любом возможном перемещении системы была равна нулю.
Принцип
возможных перемещений

Необходимость:
Пусть механическая система находится под действием внешних активных сил,
главный вектор которых:
На неё наложены голономные,
стационарные связи:
Тогда, поскольку каждая из точек системы находится в равновесии:
Просуммируем по всем точкам системы:
По определению идеальных связей:
Принцип
возможных перемещений

Достаточность:
Пусть механическая система с идеальными связями, удовлетворяющая неравенству
совершает действительное перемещение
Тогда: dT =
При стационарных связях действительные перемещения совпадают с какими-либо возможными перемещениями:
Но это противоречит условию:
Когда приложенные силы к системе удовлетворяют этому условию, система из состояния покоя выйти не может, следовательно, это условие является достаточным условием равновесия системы.
Принцип
возможных перемещений

Пример: Найти величину силы Р, удерживающей тяжелые гладкие призмы с массами m1 m2 в состоянии равновесия. Угол скоса призм равен α .
РЕШЕНИЕ ЗАДАЧ
Решение задач

Принцип возможных перемещений позволяет решать самые разнообразные задачи на равновесие механических систем – находить неизвестные активные силы, определять реакции связей, находить положения равновесия механической системы под действием приложенной системы сил.
Решение задач