Слайд 2Поток вектора напряженности – скалярное произведение вектора напряженности на вектор площади
единичный вектор,
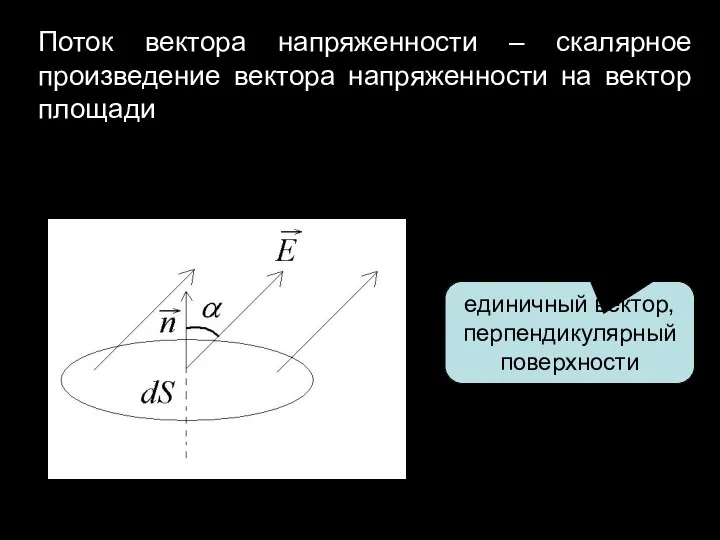
перпендикулярный поверхности
Слайд 3Рассмотрим точечный заряд. Окружим заряд сферой радиусом r.
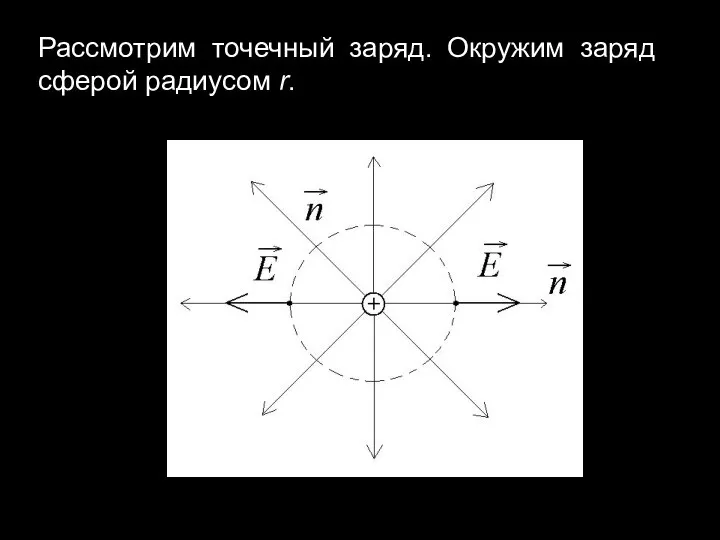
Слайд 4Поток вектора напряженности сквозь поверхность сферы равен

Слайд 5Таким образом, суммарный поток сквозь замкнутую поверхность определяется зарядом, охватываемым замкнутой поверхностью.

Слайд 6Если поверхность охватывает множество зарядов, то согласно принципу суперпозиции:

Слайд 7Суммарный поток сквозь замкнутую поверхность определяется зарядами, охватываемыми замкнутой поверхностью.

Слайд 8Теорема Гаусса в интегральной форме:
поток вектора напряженности электрического поля сквозь замкнутую

поверхность равен алгебраической сумме зарядов охватываемых этой поверхностью, делённой на ε0.
Слайд 9Поскольку суммарный заряд может быть найден интегрированием по объему
то теорема Гаусса принимает

вид:
Слайд 10Пример 1. Определение поля бесконечной нити, заряженной с линейной плотностью τ.
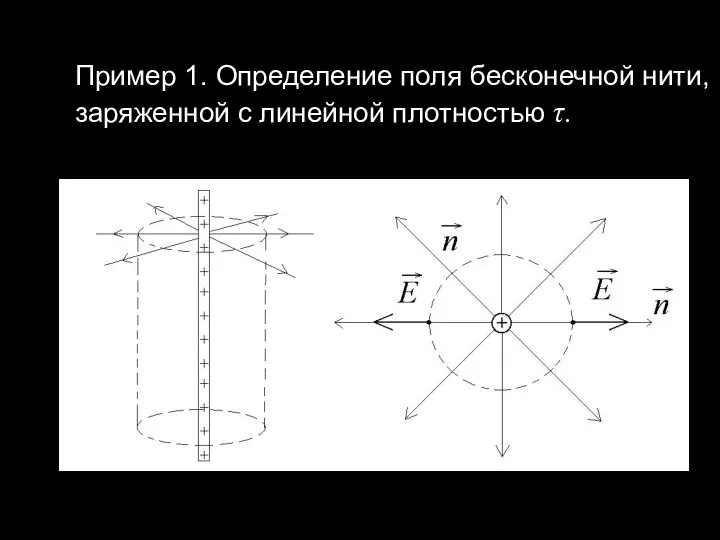
Слайд 11В качестве поверхности выберем поверхность цилиндра. Поток через поверхность, определяется только потоком

через боковую поверхность:
Слайд 12Пример 2. Найти напряженность поля двух концентрических заряженных сфер.

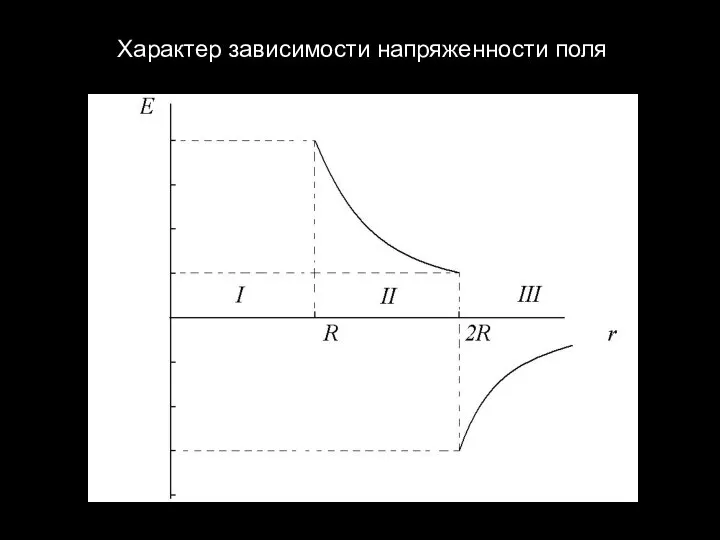
Слайд 13Поле двух концентрических сфер в трех областях.

Слайд 15Характер зависимости напряженности поля
Слайд 16Пример 3. Рассмотрим поле двух коаксиальных цилиндров.

















 Источники питания. Батареи. Аккумуляторы
Источники питания. Батареи. Аккумуляторы Стандарт для определения состояния шарнира стойки стабилизатора
Стандарт для определения состояния шарнира стойки стабилизатора Семинар по физике для 83 и 84 групп
Семинар по физике для 83 и 84 групп Физика в загадках. Своя игра
Физика в загадках. Своя игра Решение задач Разные виды движения
Решение задач Разные виды движения Работа газа и пара при расширении. Двигатель внутреннего сгорания. КПД
Работа газа и пара при расширении. Двигатель внутреннего сгорания. КПД Близкодействие и дальнодействие. Электрическое поле
Близкодействие и дальнодействие. Электрическое поле Что изучает физика?
Что изучает физика? Вимушені коливання. Резонанс (Лекція 4)
Вимушені коливання. Резонанс (Лекція 4) Презентация на тему Физические величины
Презентация на тему Физические величины  Практическое занятие. Расчет тока КЗ
Практическое занятие. Расчет тока КЗ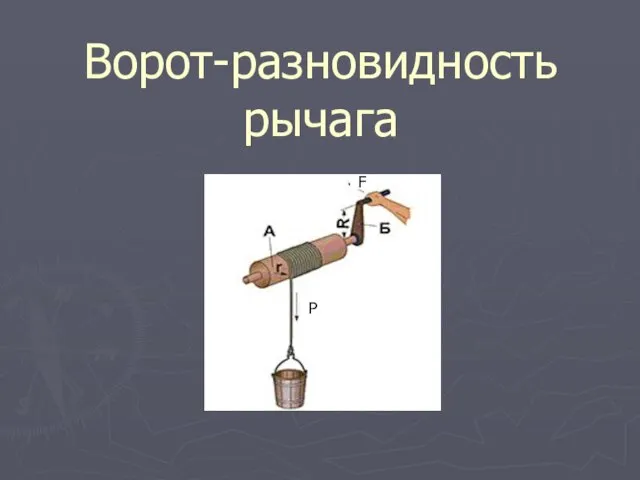 Ворот-разновидность рычага
Ворот-разновидность рычага Определение технического состояния системы питания карбюраторных и инжекторных( бензиновых двигателей)
Определение технического состояния системы питания карбюраторных и инжекторных( бензиновых двигателей) Измерительная система определения теплофизических свойств твердых и сыпучих материалов на базе прибора ИТ – 3
Измерительная система определения теплофизических свойств твердых и сыпучих материалов на базе прибора ИТ – 3 Метод конденсации в среде инертного газа
Метод конденсации в среде инертного газа Внутренняя энергия идеального газа и степени свободы
Внутренняя энергия идеального газа и степени свободы Презентация на тему Золотое правило механики (7 класс)
Презентация на тему Золотое правило механики (7 класс)  Радиоактивность. Ядерные реакции
Радиоактивность. Ядерные реакции Тематический состав ВсОШ по физике для 9-ого класса
Тематический состав ВсОШ по физике для 9-ого класса Механические колебания и волны. Звук. Решение заданий ОГЭ
Механические колебания и волны. Звук. Решение заданий ОГЭ Оптическая дифракционная решетка
Оптическая дифракционная решетка Смазка для подшипников
Смазка для подшипников Статистика неисправностей холодильников
Статистика неисправностей холодильников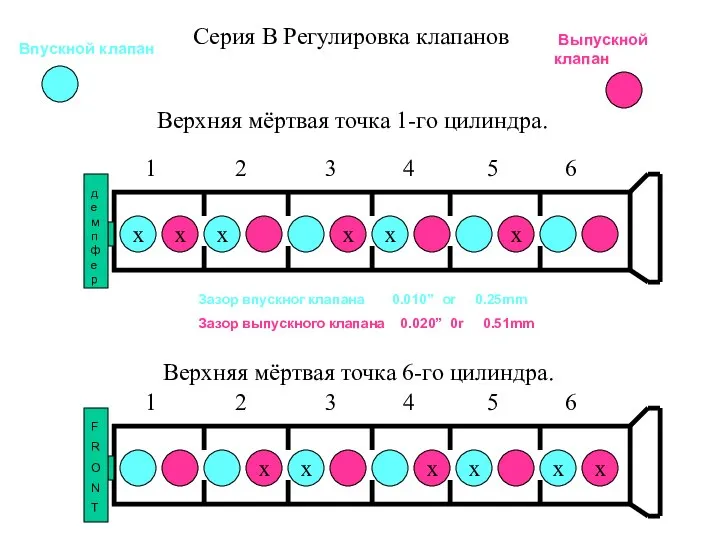 Регулировка клапанов цилиндра
Регулировка клапанов цилиндра Опыты дома
Опыты дома Научные открытия и изобретения. Водяной двигатель
Научные открытия и изобретения. Водяной двигатель 3-й закон Ньютона
3-й закон Ньютона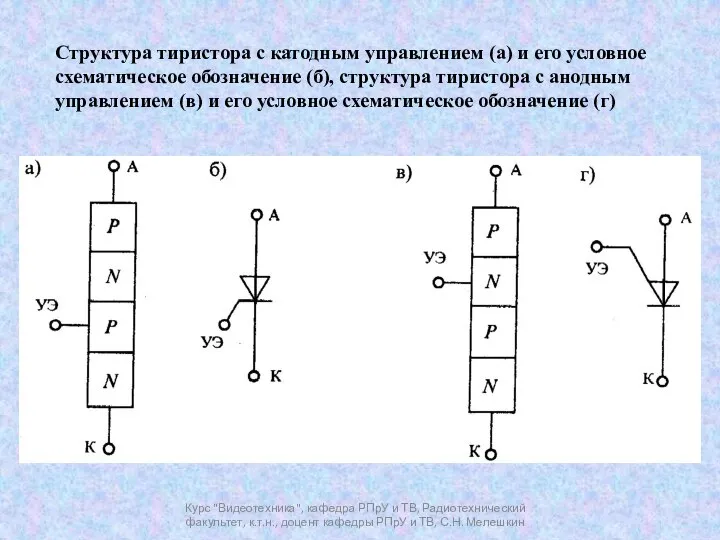 Тиристор
Тиристор