Содержание
- 2. Литература Учебники 1. Тарг С.М. Краткий курс теоретической механики. 2. Яблонский А.А. Курс теоретической механики. Часть
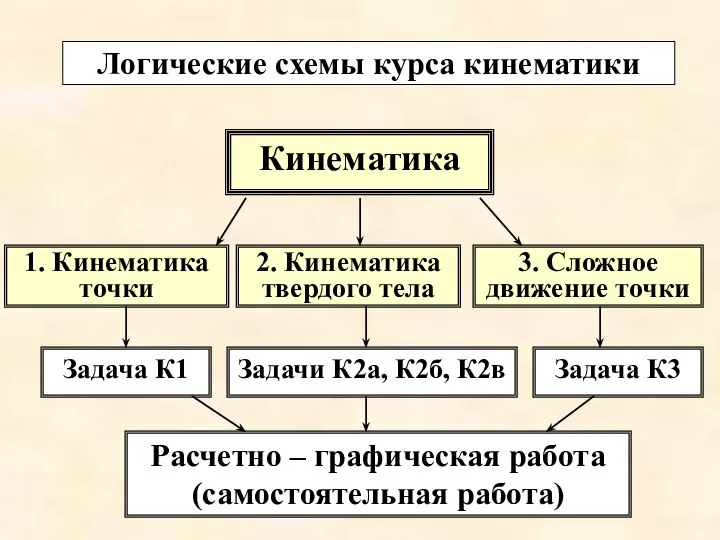
- 3. Логические схемы курса кинематики Кинематика 1. Кинематика точки 2. Кинематика твердого тела 3. Сложное движение точки
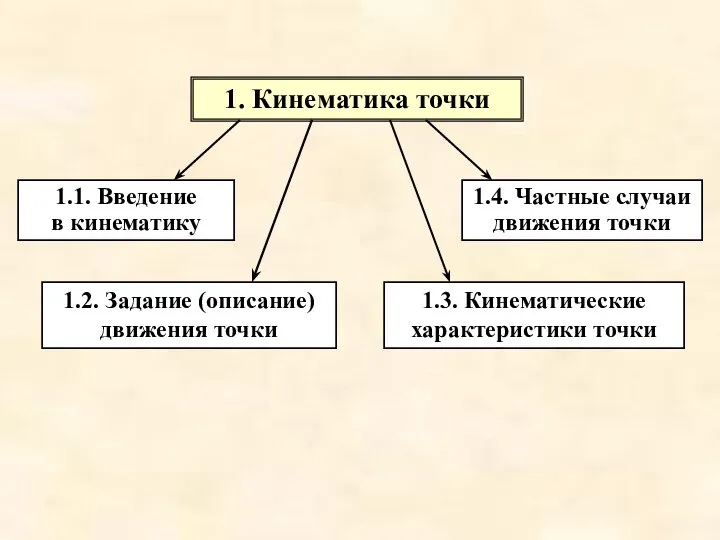
- 4. 1. Кинематика точки 1.1. Введение в кинематику 1.2. Задание (описание) движения точки 1.3. Кинематические характеристики точки
- 5. 1.1. Введение в кинематику Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без
- 6. Основные определения кинематики Пространство Пространство в механике рассматривается как трехмерное евклидово. Все измерения в нем производятся
- 7. Для определения положения движущегося тела (или точки) в разные моменты времени вводят систему отсчета (систему координат),
- 8. Свойство времени, принятого в механике Время в механике считается универсальным, т. е. протекающим одинаково во всех
- 9. Время t – скалярная, непрерывно изменяющаяся, величина. В кинематике - независимая переменная (аргумент). Характеристики универсального времени
- 10. Промежутком времени △t называется разность между какими – нибудь последовательными моментами времени: △ t = t2
- 11. Способы задания движения точки Движение точки называется прямолинейным, если ее траекторией является прямая линия, а если
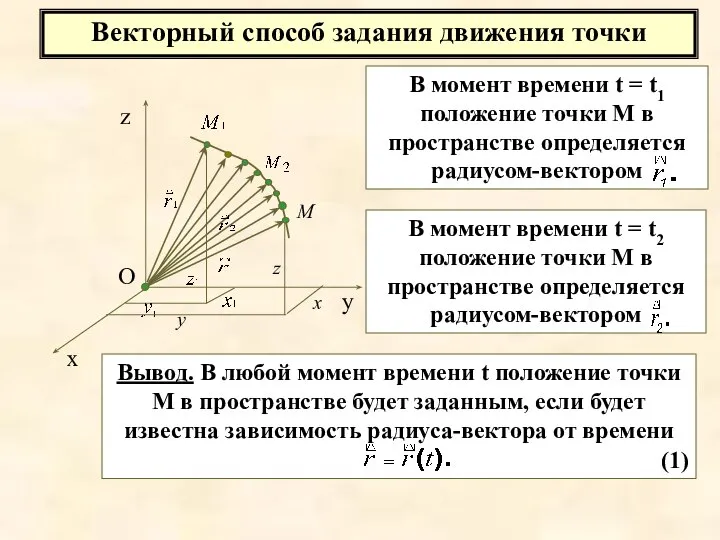
- 12. Векторный способ задания движения точки В момент времени t = t1 положение точки М в пространстве
- 13. Опр. Геометрическое место концов вектора , т. е. годограф этого вектора, определяет траекторию движущейся точки. Вывод.
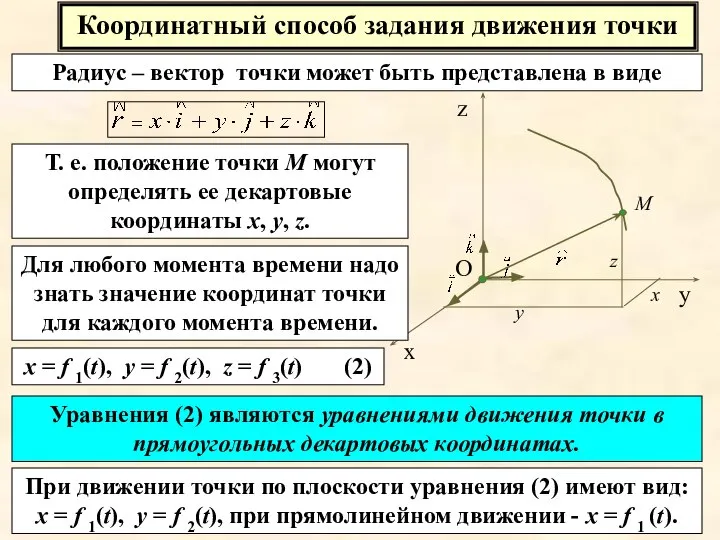
- 14. Координатный способ задания движения точки Радиус – вектор точки может быть представлена в виде Т. е.
- 16. Скачать презентацию









 Теоретические основы электротехники. Трехфазные электрические цепи
Теоретические основы электротехники. Трехфазные электрические цепи Значение закона сохранения импульса
Значение закона сохранения импульса Задача на преломление луча в плоскопараллельной пластине
Задача на преломление луча в плоскопараллельной пластине Длина волны. Связь длины волны со скоростью ее распространения и периодом. Уравнение волны
Длина волны. Связь длины волны со скоростью ее распространения и периодом. Уравнение волны Проект воздухоразделительной установки №7 в условиях АО Уральская Сталь
Проект воздухоразделительной установки №7 в условиях АО Уральская Сталь Постоянные магниты. Магнитное поле постоянных магнитов
Постоянные магниты. Магнитное поле постоянных магнитов Механическое движение. Равномерное движение
Механическое движение. Равномерное движение Физика. 10 класс
Физика. 10 класс 1435976
1435976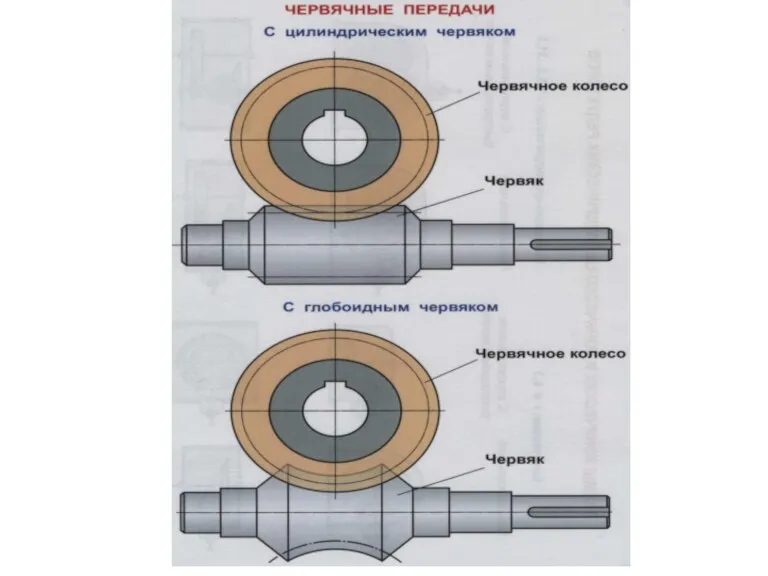 Червячные передачи
Червячные передачи Движение твердой среды
Движение твердой среды Применение метода стабилизации связей к задачам неголономной механики
Применение метода стабилизации связей к задачам неголономной механики Динамическая метеорология. Термический ветер
Динамическая метеорология. Термический ветер Ремонт электрических машин всех типов
Ремонт электрических машин всех типов Сила Лоренца. Действие магнитного поля на движущуюся заряженную частицу
Сила Лоренца. Действие магнитного поля на движущуюся заряженную частицу Элементы машиноведения. Составные части машин
Элементы машиноведения. Составные части машин Расчет пролетного строения. Расчет плиты балластного корыта. Расчет главной балки.Лекция №7
Расчет пролетного строения. Расчет плиты балластного корыта. Расчет главной балки.Лекция №7 Нагревание проводников электрическим током. Закон Джоуля-Ленца
Нагревание проводников электрическим током. Закон Джоуля-Ленца Тест. Вес тела. Связь между массой тела и силой тяжести
Тест. Вес тела. Связь между массой тела и силой тяжести Пляшущий мяч
Пляшущий мяч Электростатика
Электростатика Соединение проводников
Соединение проводников Средства измерений и контроля с оптическим и оптико-механическим преобразованием
Средства измерений и контроля с оптическим и оптико-механическим преобразованием Решение задач по теме Основы термодинамики
Решение задач по теме Основы термодинамики Демонстрационный материал по физике для 9-го класса
Демонстрационный материал по физике для 9-го класса Лекция 3. Действующее и среднее значение переменного тока или напряжения
Лекция 3. Действующее и среднее значение переменного тока или напряжения Дисперсия световых волн
Дисперсия световых волн Деформация, механические свойства и разрушение металлов (Лекция 4)
Деформация, механические свойства и разрушение металлов (Лекция 4)