Содержание
- 2. Литература ОСНОВНАЯ 1. Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: Учеб./ Е.А. Волков, Э.И.
- 3. Структура курса Цепи с сосредоточенными параметрами (2 семестр 2 курса). Лекции, практические занятия, контрольные задания, тесты,
- 4. Лекция 1. Введение. Основная задача ТЦ- изучение методов анализа и синтеза электрических цепей. Задача анализа -
- 5. Электрическая цепь - совокупность элементов и устройств, образующих путь или пути для электрического тока
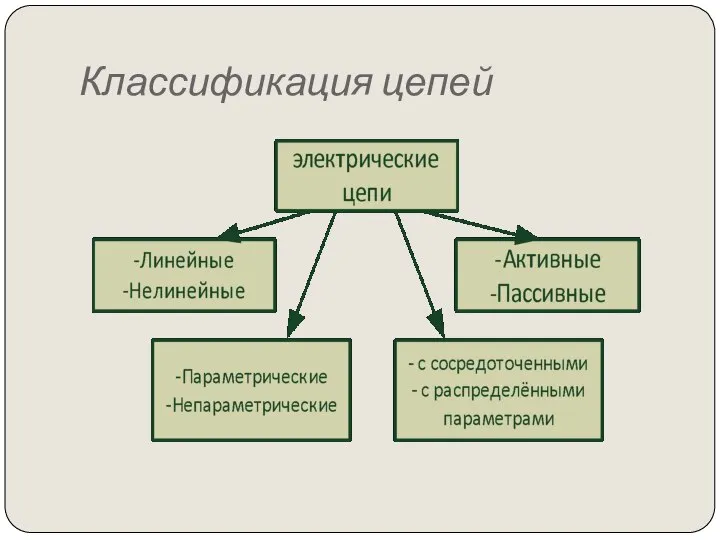
- 6. Классификация цепей
- 7. Линейные цепи Цепи, составленные из линейных элементов. Связь между Э, U, I выражается линейными уравнениями (
- 8. Нелинейные цепи Цепи в которые входят пассивные элементы, электрическое сопротивление которых существенно зависит от тока или
- 9. Примечание И к линейным и к нелинейным цепям применимы законы Кирхгофа, которые имеют общий характер. Но
- 10. Активными называются цепи, содержащие источники электрической энергии. Параметрическими - электрические цепи, в которых хотя бы один
- 11. Цепи с сосредоточенными параметрами
- 12. Цепи с распределённым параметрами –цепи, в которых ЭМ поле и потери равномерно или неравномерно распределены вдоль
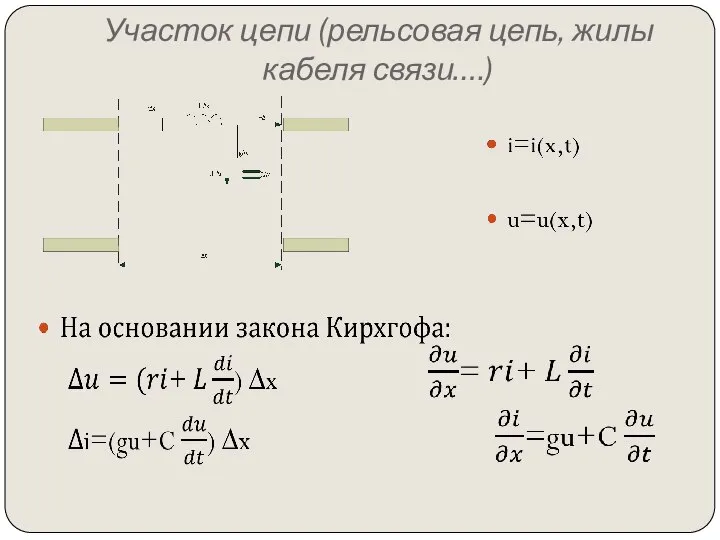
- 13. Участок цепи (рельсовая цепь, жилы кабеля связи….)
- 14. Классификация цепей по типу дифференциального уравнения не является единственным признаком. В зависимости от топологических особенностей электрические
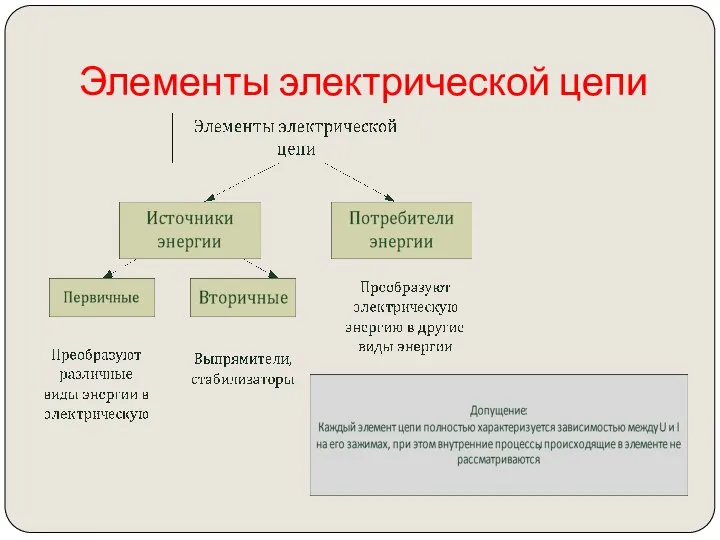
- 15. Элементы электрической цепи
- 16. Элементы электрической цепи Активные –способны поставлять энергию в цепь. Пассивные –способны накапливать и расходовать энергию. Идеальные
- 17. Идеальный активный элемент: независимый источник напряжения (э.д.с. или u(t), Rвн=0) независимый источник тока (I, i(t), Rвн=∞)
- 18. Реальная линейная цепь включает в себя резисторы, конденсаторы, катушки индуктивности, трансформаторы, диоды, транзисторы, операционные усилители, источники
- 19. Каждый из процессов в цепях связывают с определенным элементом: например, превращение энергии в тепло связано с
- 20. Идеальный резистивный элемент
- 21. Схема замещения резистора основная функция резистора – превращение электрической энергии в тепло он имеет выводы, которыми
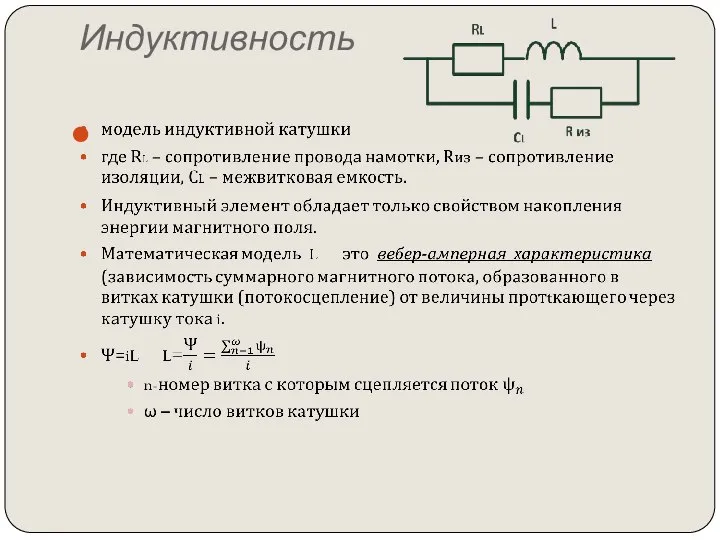
- 23. Индуктивность
- 24. Ёмкостной элемент
- 25. Конденсатор имеет выводы, с помощью которых он устанавливается в устройство, следовательно, он имеет индуктивность выводов. Кроме
- 26. В моделях R, L, C – это идеальные элементы (сопротивление, индуктивность, емкость), т.е. в них происходит
- 27. Скин-эффект Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей
- 28. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на
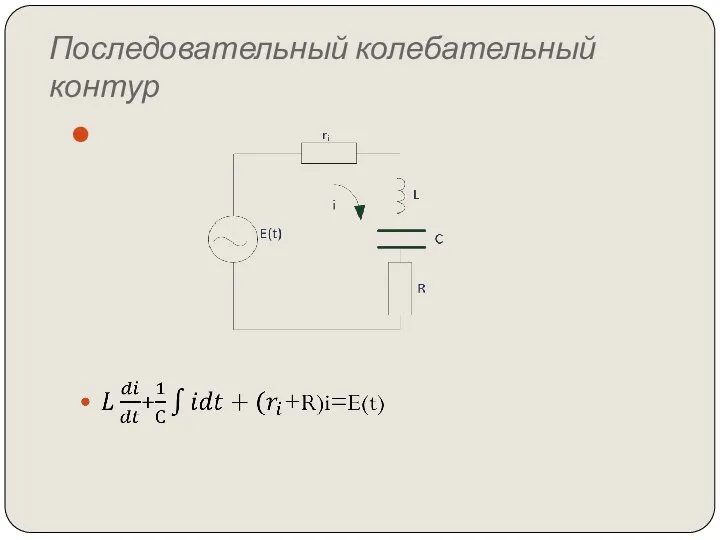
- 29. Последовательный колебательный контур
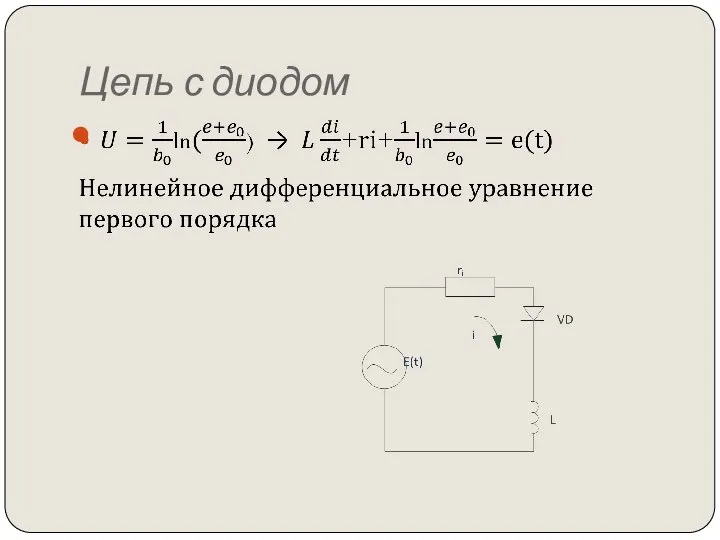
- 30. Цепь с диодом
- 31. Электромагнитные поля и электрические цепи Электромагнитное поле –особая форма материи. Посредством ЭМ поля осуществляется взаимодействие между
- 32. Уравнения Максвелла
- 33. Уравнения Максвелла
- 34. Уравнения Максвелла
- 35. 2. Режим гармонических колебаний в линейных электрических цепях Простейший вариант периодических колебаний - гармонические, когда колеблющаяся
- 36. Важность гармонических колебаний Широко используются для передачи сигналов и электрической энергии Удобно использовать как испытательный сигнал
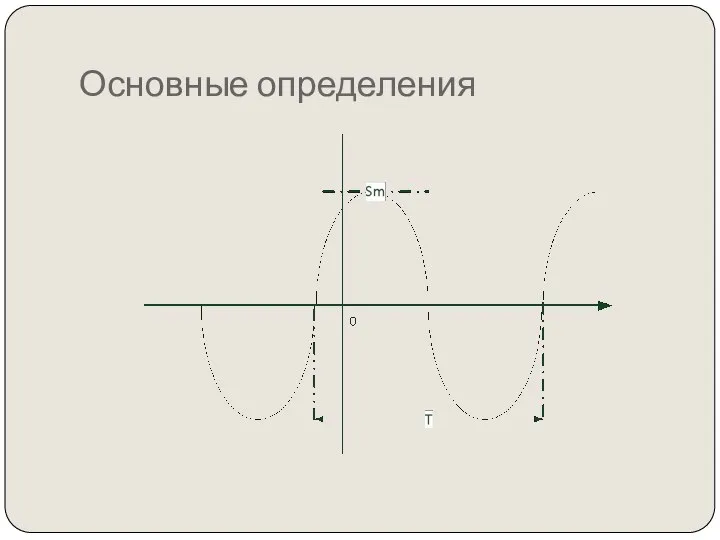
- 37. Основные определения S(t)=Smcos(ωt+ϕ0)=Smcosϴ(t) Sm- амплитуда колебаний - наибольшее по абсолютному значению отклонение колеблющейся величины. ϴ(t) =(ωt+ϕ0)
- 38. Основные определения ω= dϴ/dt –круговая частота (угловая скорость)- определяет скорость изменения фазы, выражается в (рад/с), т.е.
- 39. Основные определения
- 40. Операции над гармоническими колебаниями
- 41. Операции над гармоническими колебаниями
- 42. (-1 ≤cos(ϕ01- ϕ02) ≤1) Если ϕ01- ϕ02=0 -амплитуда максимальна Sm=S1m+Sm2 Если ϕ01- ϕ02=±π -амплитуда минимальна Sm=
- 43. Выводы Линейные операции над гармонической функцией приводят только к изменению её амплитуды и начальной фазы. Наложение
- 44. Энергетические характеристики гармонических колебаний Мгновенная мощность Средняя мощность Действующее (эффективное) значение амплитуды напряжения и тока
- 45. Мгновенная мощность
- 46. Средняя мощность Средняя ( активная) мощность произвольных колебаний определяется как отношение энергии, подведённой к цепи за
- 47. Среднеквадратичные значения напряжений и токов(действующие, эффективные)
- 48. Характеристики линейных электрических цепей Свойства электрической цепи определяются реакцией её на то или иное воздействие. В
- 49. Выполнение этих требований даёт возможность при расчете реакции цепи на сложное воздействие применять принцип суперпозиции: найдя
- 50. Применение принципа наложения существенно облегчает решение многих задач в линейных электрических цепях. Весь дальнейший материал будет
- 51. В качестве тестовых сигналов применяют гармоническую функцию единичной амплитуды u = cosω t , u =
- 52. Отрезок гармонического колебания
- 53. Единичный скачок (функция Хевисайда)
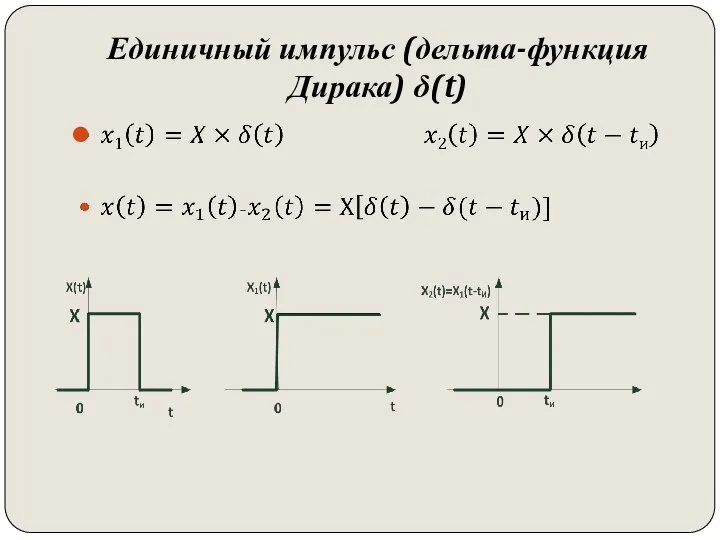
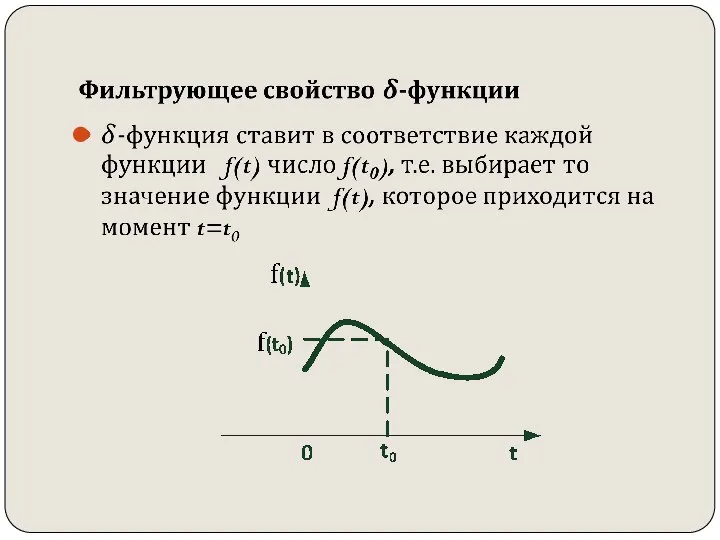
- 55. Единичный импульс (дельта-функция Дирака) δ(t)
- 57. Свойства дельта-функции Дирака δ(t)
- 60. Связь единичного импульса и единичного скачка
- 61. Временное представление
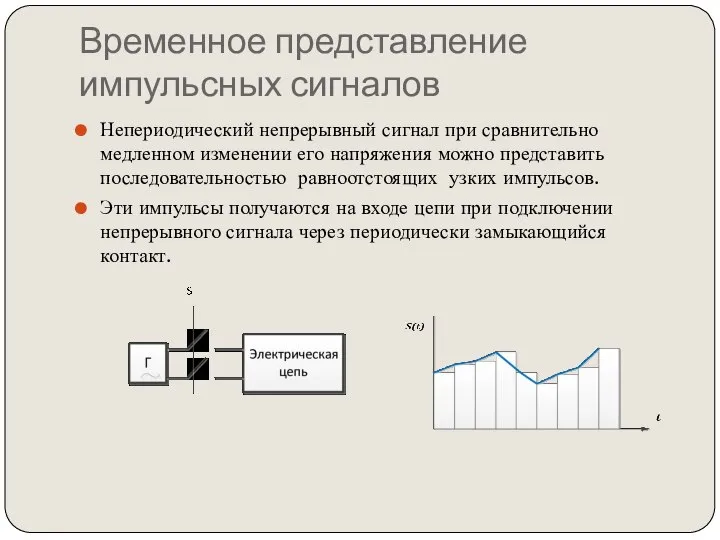
- 62. Временное представление импульсных сигналов Непериодический непрерывный сигнал при сравнительно медленном изменении его напряжения можно представить последовательностью
- 64. Частотное представление импульсных сигналов Периодическая непрерывная функция времени имеет дискретный линейчатый непериодический спектр. На основании симметрии
- 65. Операторное представление импульсных сигналов
- 66. Реакции на тестовые сигналы 1. Комплексная характеристика –реакция цепи при нулевых начальных условиях на гармонический тестовый
- 67. Перечисленные характеристики могут относиться как к характеристикам передачи (в этом случае они называются соответственно комплексным коэффициентом
- 68. Входные сопротивления вычисляются как отношение входного напряжения к входному току, а проводимость - величина, обратная входному
- 69. Начальные условия
- 70. Комплексный коэффициент передачи цепи К(jω)
- 71. Комплексный коэффициент передачи цепи К(jω) ǀK(jω)ǀ - модуль комплексного числа- называется АЧХ(амплитудно-частотной характеристикой цепи), она показывает
- 72. Операторное, частотное и временное представление непрерывных и импульсных воздействий и реакций цепей. элементарные тестовые сигналы: sinωt,
- 73. Лекция №2 «Канонические схемы двухполюсников RC, RL и LC, свойства их сопротивлений и проводимостей»
- 74. Определение двухполюсника Двухполюсником называется любая электрическая цепь, рассматриваемая относительно двух зажимов, т.е. имеющая два внешних зажима.
- 76. Классификация двухполюсников Двухполюсники бывают линейные и нелинейные. Двухполюсник будет линейным, если он не содержит в своем
- 77. По характеру элементов двухполюсники могут быть реактивные и диссипативные. Реактивные двухполюсники состоят только из индуктивностей и
- 78. Активные и пассивные Пассивный двухполюсник не имеет внутри себя источников энергии и поэтому мощность на нём
- 79. Любой двухполюсник может быть охарактеризован своей входной функцией: Это может быть: Z(jω)-входное сопротивление Y(jω)-входная проводимость
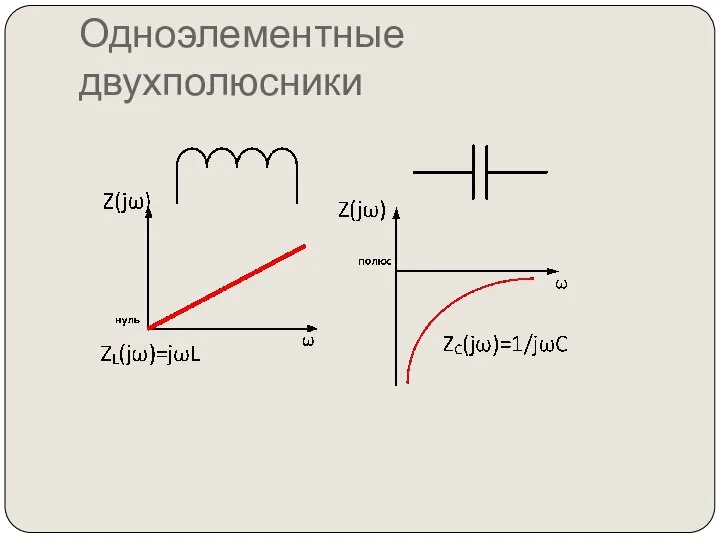
- 80. Одноэлементные двухполюсники
- 81. Частоты, на которых величина входного сопротивления двухполюсника становится равной нулю (Zвх=0)называются нулями входной функции. Частоты, на
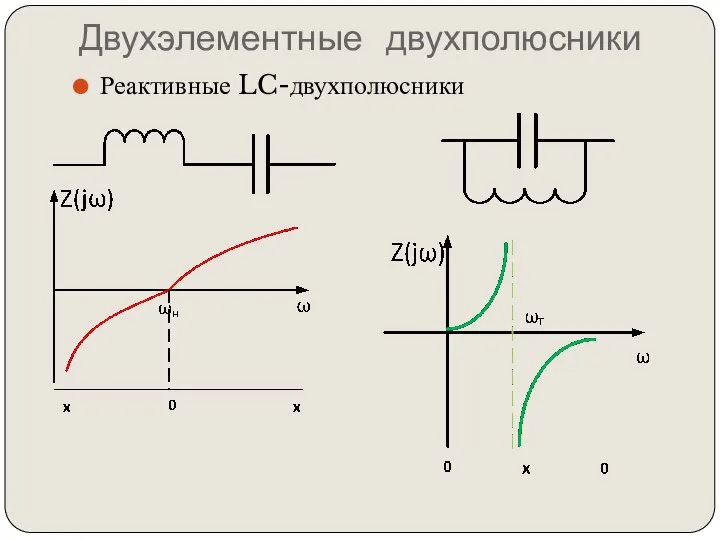
- 82. Двухэлементные двухполюсники Реактивные LC-двухполюсники
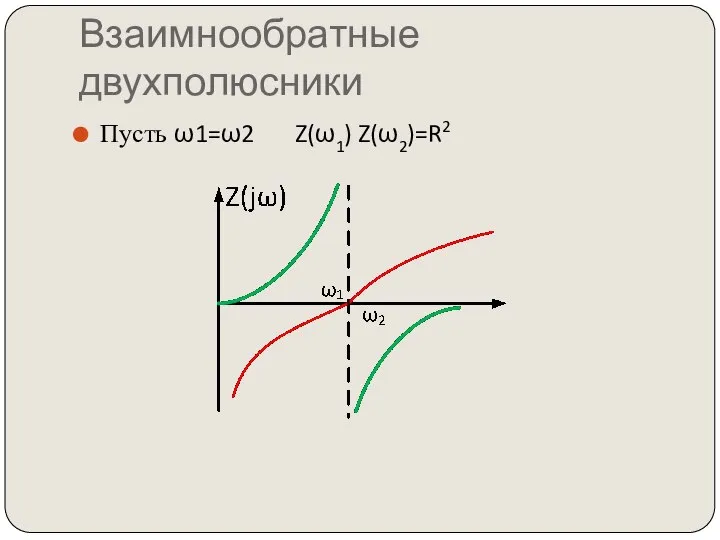
- 83. Взаимнообратные двухполюсники Пусть ω1=ω2 Z(ω1) Z(ω2)=R2
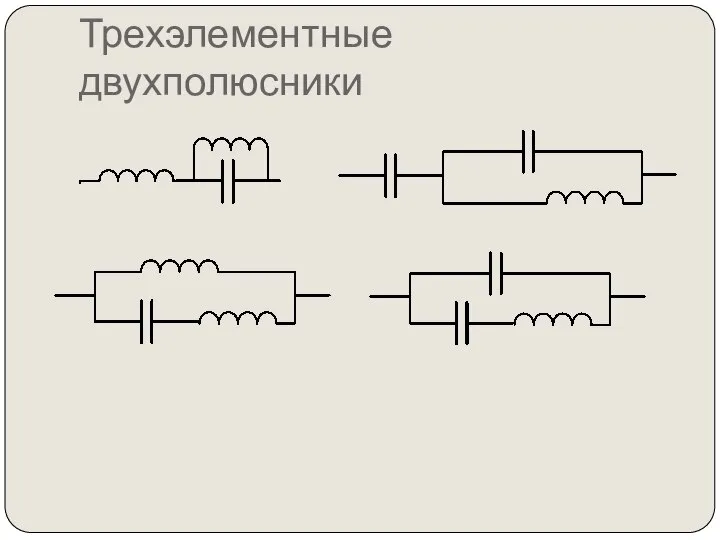
- 84. Трехэлементные двухполюсники
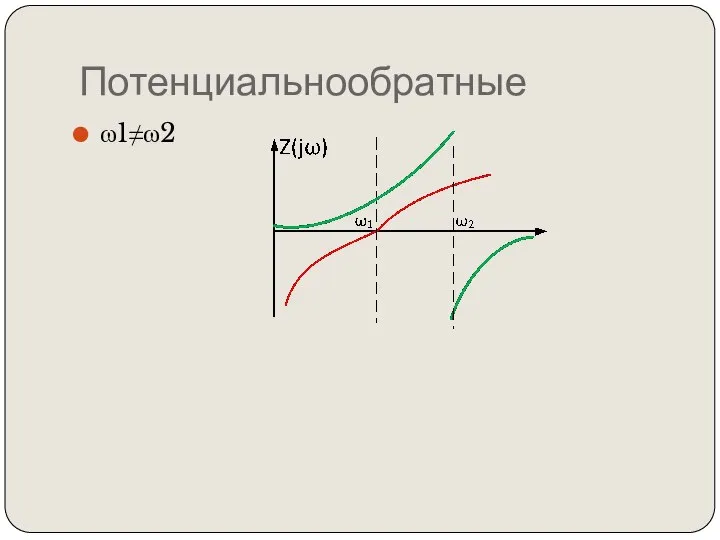
- 85. Потенциальнообратные ω1≠ω2
- 86. Общие свойства двухполюсников 1. Число резонансных частот любого реактивного двухполюсника на единицу меньше общего числа реактивных
- 88. Скачать презентацию






































































 Решение задач на силу Ампера и силу Лоренца. Урок 51
Решение задач на силу Ампера и силу Лоренца. Урок 51 Механические колебания
Механические колебания Плотность вещества
Плотность вещества Прямолинейное равномерное движение
Прямолинейное равномерное движение Микроподводные движители. Виды микро-движителей
Микроподводные движители. Виды микро-движителей Лазерные фазовые дальномеры
Лазерные фазовые дальномеры Презентация на тему Конденсаторы (10 класс)
Презентация на тему Конденсаторы (10 класс)  Стенд для лабораторных работ Зубчатые передачи
Стенд для лабораторных работ Зубчатые передачи Давление твёрдых тел, жидкостей и газов
Давление твёрдых тел, жидкостей и газов Антенна. Классификация радиопередающих устройств
Антенна. Классификация радиопередающих устройств Процедура работы с браком
Процедура работы с браком Магнитное поле
Магнитное поле Автомобили. 3 класс
Автомобили. 3 класс Атом - сложная частица
Атом - сложная частица МФТИ 5 вариант. Подготовка к ЕГЭ
МФТИ 5 вариант. Подготовка к ЕГЭ Внешний фотоэффект. Изучение законов внешнего фотоэффекта
Внешний фотоэффект. Изучение законов внешнего фотоэффекта Презентация на тему Робототехника и Искусственный Интеллект
Презентация на тему Робототехника и Искусственный Интеллект  Сила упругости. Закон Гука. Вес тела
Сила упругости. Закон Гука. Вес тела Линзы. Виды линз. Условное обозначение линз. Собирающие линзы
Линзы. Виды линз. Условное обозначение линз. Собирающие линзы Свойства металлов и сплавов
Свойства металлов и сплавов Лабораторная работа Определение положения центра тяжести плоской фигуры
Лабораторная работа Определение положения центра тяжести плоской фигуры Введение в гидродинамику
Введение в гидродинамику Мир без денег – это возможно?
Мир без денег – это возможно? Закон Ома, расчёт сопротивления, виды соединения проводников. Подготовка к контрольной
Закон Ома, расчёт сопротивления, виды соединения проводников. Подготовка к контрольной Классификация композитов. Волокна и матрицы. Структура и назначение
Классификация композитов. Волокна и матрицы. Структура и назначение Полупроводники. Проводимость полупроводников
Полупроводники. Проводимость полупроводников Динамика поступательного движения
Динамика поступательного движения Основные потребители реактивной мощности на промышленных предприятиях. Основные принципы размещения компенсирующих устройств
Основные потребители реактивной мощности на промышленных предприятиях. Основные принципы размещения компенсирующих устройств