Содержание
- 2. Теория упругости имеет целью аналитическое изучение напряженно-деформированного состояния упругого тела. С помощью теории упругости могут быть
- 3. В математической линейной теории упругости исходят из следующих допущений: 1. О непрерывности (сплошности) среды. При этом
- 4. 4. О шаровой изотропности, на основании которого считается, что механические свойства материала одинаковы по всем направлениям.
- 5. При решении задач теории упругости часто пользуются принципом Сен-Венана: если внешние силы, приложенные на небольшом участке
- 6. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 18 ВНЕШНИЕ СИЛЫ (нагрузки) Поверхностные Объемные – результат непосредственного контактного взаимодействия тела
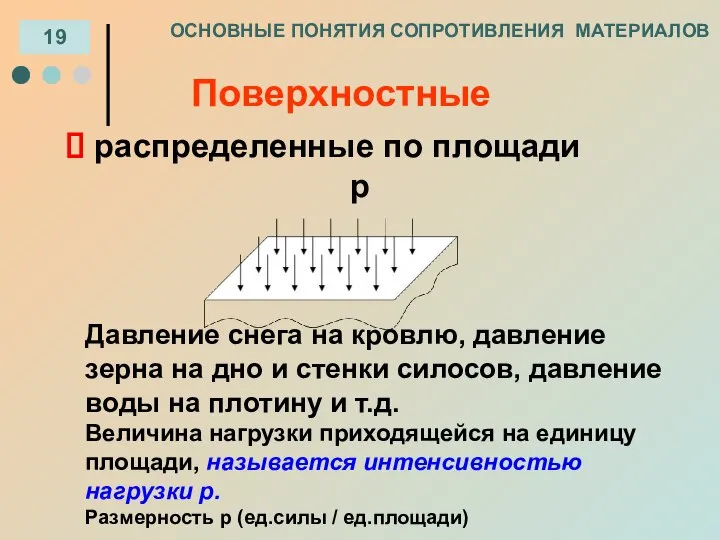
- 7. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 19 распределенные по площади р Давление снега на кровлю, давление зерна на
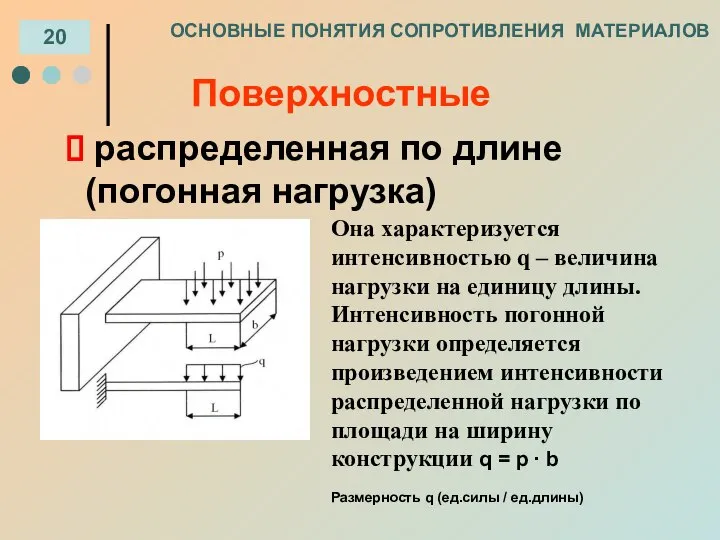
- 8. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 20 распределенная по длине (погонная нагрузка) Поверхностные Она характеризуется интенсивностью q –
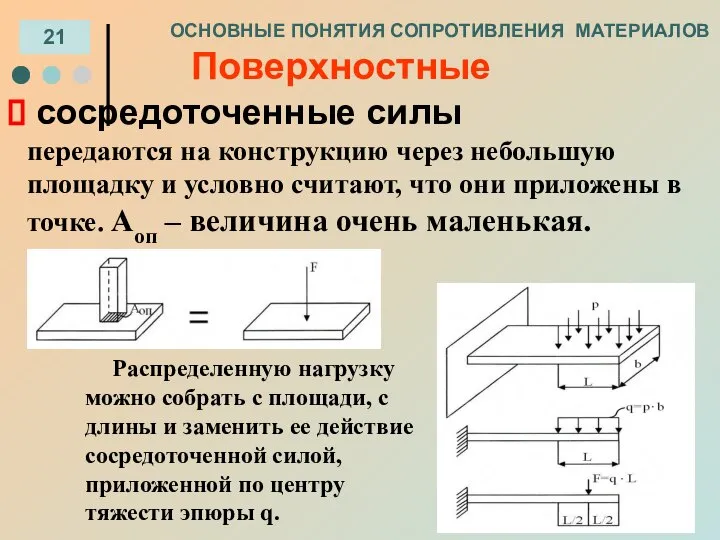
- 9. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 21 сосредоточенные силы передаются на конструкцию через небольшую площадку и условно считают,
- 10. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 22 приложены к каждой точке объема. Это – собственный вес, центробежные силы,
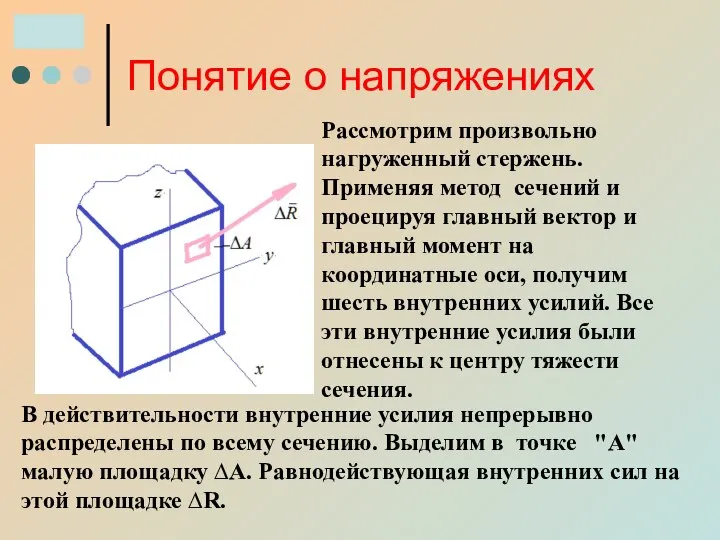
- 11. Понятие о напряжениях Рассмотрим произвольно нагруженный стержень. Применяя метод сечений и проецируя главный вектор и главный
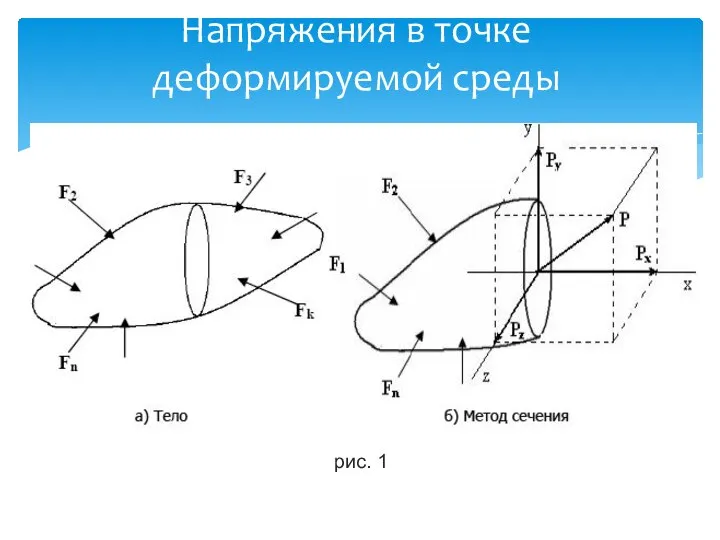
- 12. Напряжения в точке деформируемой среды рис. 1
- 13. Полное напряжение в точке определяют как предел отношения: Нормальное напряжение в точке определяют как предел отношения
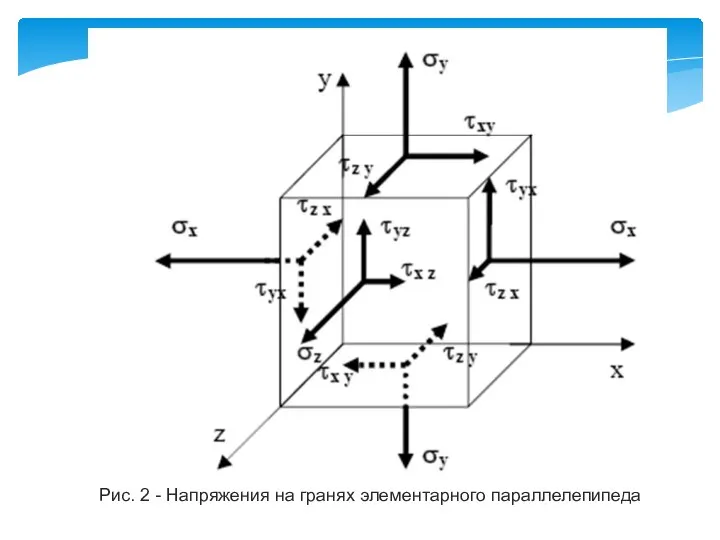
- 14. Рис. 2 - Напряжения на гранях элементарного параллелепипеда
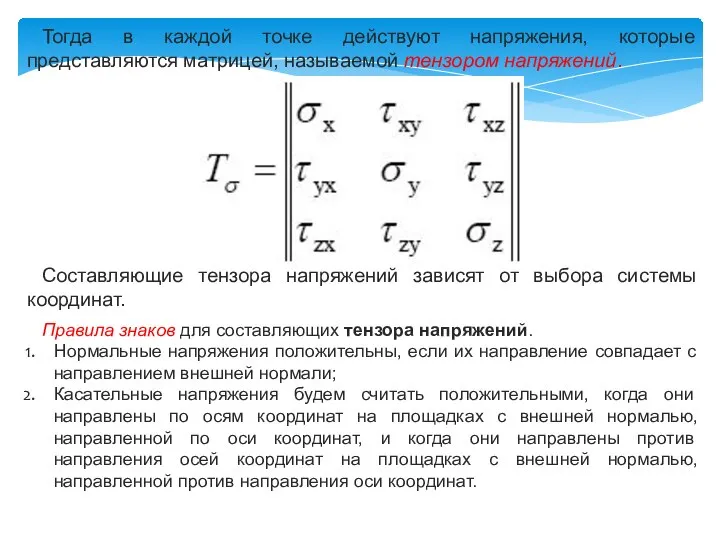
- 15. Тогда в каждой точке действуют напряжения, которые представляются матрицей, называемой тензором напряжений. Составляющие тензора напряжений зависят
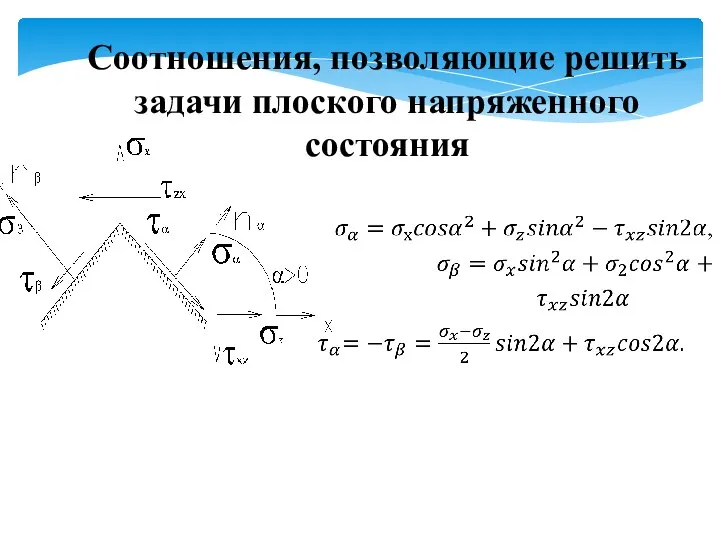
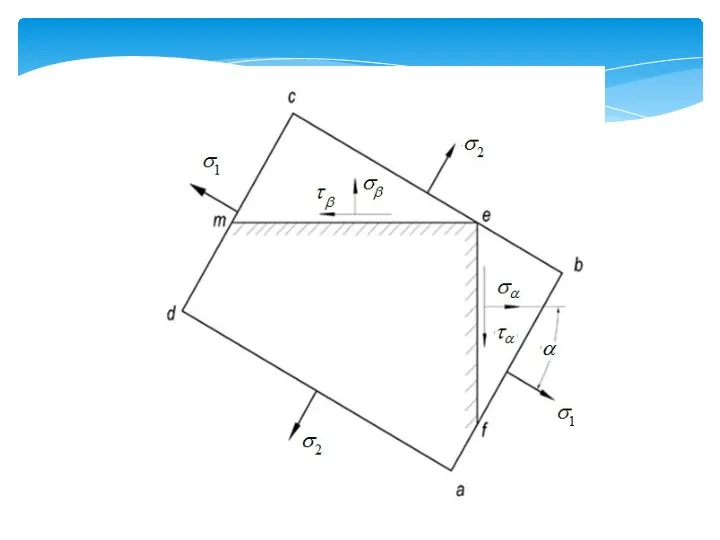
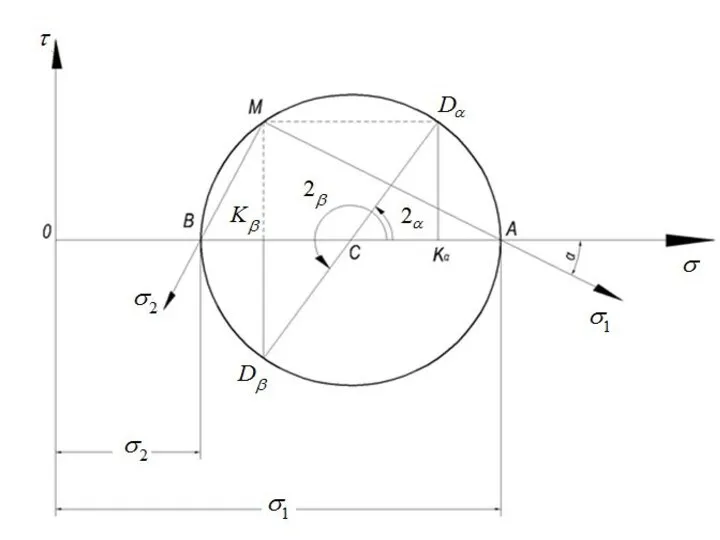
- 16. Соотношения, позволяющие решить задачи плоского напряженного состояния
- 17. Максимальные напряжения действует на площадке ближайшей к наклонной площадке с большим нормальным напряжением. Из сказанного выше
- 21. Дифференциальные уравнения равновесия (уравнения Навье)
- 22. Ввиду бесконечной малости параллелепипеда принято, что напряжения во всём его объёме остаются неизменяемыми (однородное напряжённое состояние).
- 24. Рассмотрим напряжения, параллельные оси х: σ x , τ xy , τxz Если на левой грани
- 25. При выводе уравнений равновесия проекций сил элементарные силы на поверхностях граней параллелепипеда получаем перемножением напряжений на
- 26. Полученные три дифференциальных уравнения равновесия называются уравнениями Навье. Если для параллелепипеда аналогично расписать три уравнения статики
- 27. Согласно этому закону по двум взаимно перпендикулярным площадкам составляющие касательных напряжений, перпендикулярные линиям пересечения этих площадок,
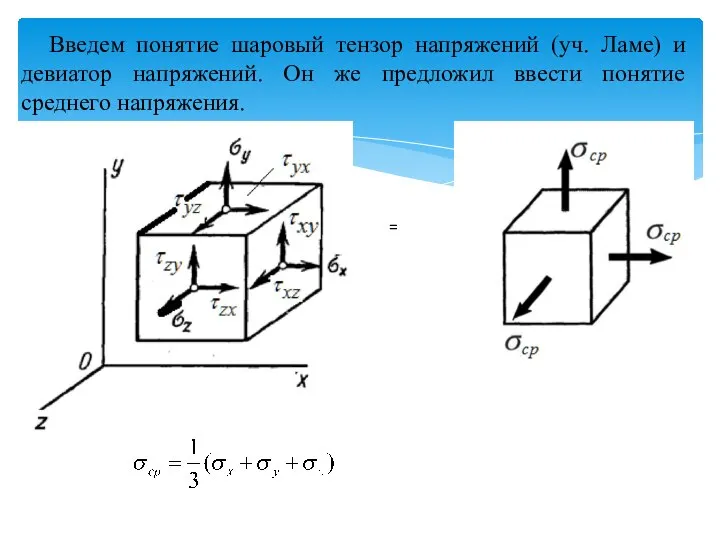
- 28. Шаровой тензор и девиатор напряжений
- 29. = Введем понятие шаровый тензор напряжений (уч. Ламе) и девиатор напряжений. Он же предложил ввести понятие
- 30. Так как тело по-разному сопротивляется равномерному всестороннему давлению и касательным напряжениям, то удобно представить тензор напряжений
- 31. Тензор деформаций. Связь между перемещениями и деформациями (формулы Коши)
- 32. Если упругое тело закрепить так, чтобы оно не могло перемещаться как абсолютно твёрдое тело, и приложить
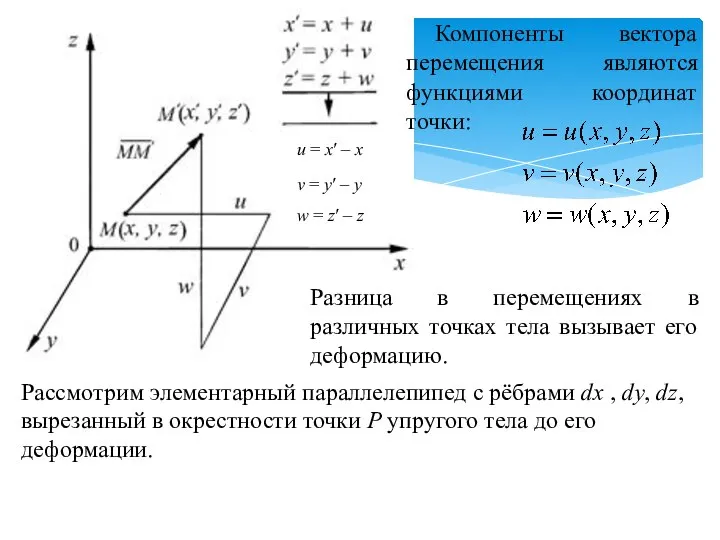
- 33. u = x′ – х v = y′ – y w = z′ – z Компоненты
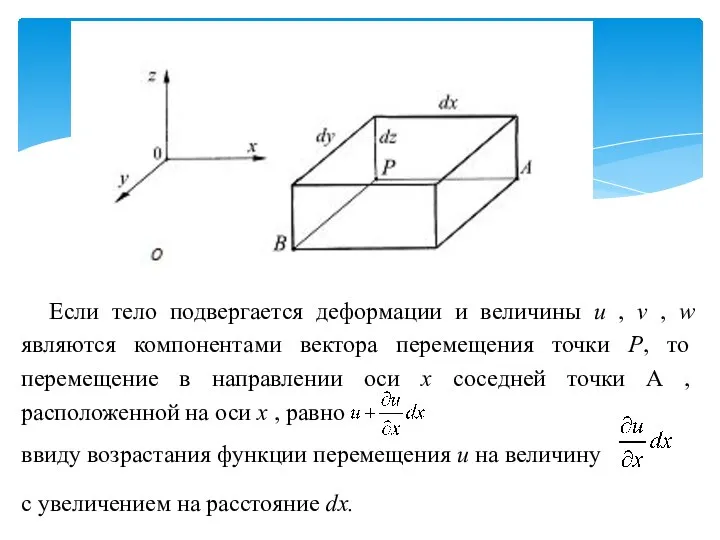
- 34. Если тело подвергается деформации и величины u , v , w являются компонентами вектора перемещения точки
- 35. Увеличение длины ребра PA , т. е. его абсолютное удлинение, вызванное деформацией, равно Тогда линейная деформация
- 36. Рассмотрим изменение угла между элементами PA и PB при деформации параллелепипеда. Пусть точка Р получила перемещения
- 37. Расстояние Из треугольника находим Ограничиваясь рассмотрением малых деформаций, можно полагать, что Точно так же направление повёрнуто
- 38. Таким же способом можно получить угловые деформации в плоскостях y, z и x, z . В
- 39. Условие совместимости деформаций
- 40. Сформулируем определение понятия «деформированное состояние в точке» как совокупность линейных и угловых деформаций для всевозможных направлений
- 41. Правило знаков деформаций : положительным линейным деформациям соответствуют удлинения вдоль осей координат, отрицательным –укорочения; положительным угловым
- 42. Сложнее обстоит дело с обратной постановкой задачи. Если заданы шесть функций деформаций, то для определения трёх
- 43. Продифференцируем дважды первые два уравнения по y и по x, соответственно. Складывая их почленно, получаем дифференциальное
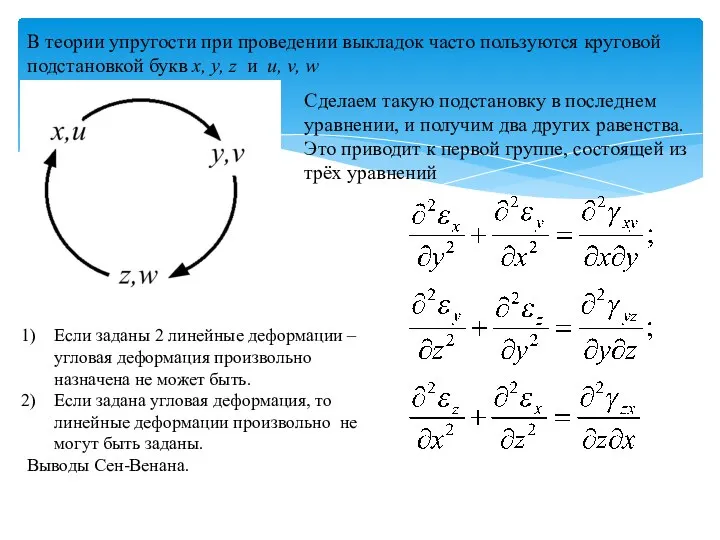
- 44. В теории упругости при проведении выкладок часто пользуются круговой подстановкой букв x, y, z и u,
- 45. Обобщённый закон Гука
- 46. Английский естествоиспытатель Роберт Гук в 1660 г. открыл закон, названный его именем. Этот закон устанавливает линейную
- 51. Чтобы установить зависимость между компонентами тензоров деформаций и напряжений при объёмном напряжённом состоянии, выделим из тела
- 53. Скачать презентацию



































 Перепад давления
Перепад давления Ферромагнетики. Относительная магнитная проницаемость вещества
Ферромагнетики. Относительная магнитная проницаемость вещества Термодинамика. Фазовые переходы
Термодинамика. Фазовые переходы Краткие сведения из физической оптики. Явления дифракции, дисперсии, интерференции. Лазерные источники излучения. Лекция №3
Краткие сведения из физической оптики. Явления дифракции, дисперсии, интерференции. Лазерные источники излучения. Лекция №3 Разветвленные цепи. Правила Кирхгофа
Разветвленные цепи. Правила Кирхгофа Энергия связи
Энергия связи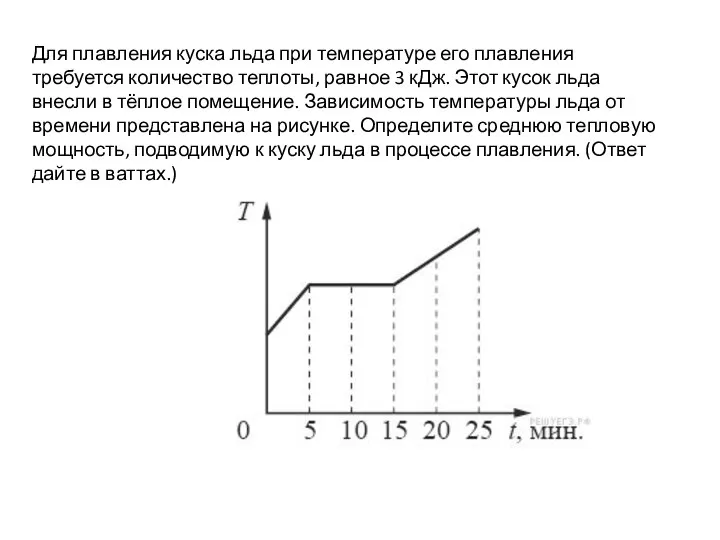 Определение тепловой мощности. ВПР, 9 класс
Определение тепловой мощности. ВПР, 9 класс Решение задач с помощью законов Ньютона
Решение задач с помощью законов Ньютона Приёмы целеполагания на уроках открытия новых знаний на уроках физики
Приёмы целеполагания на уроках открытия новых знаний на уроках физики Простые механизмы
Простые механизмы Теоретическая механика. Кинематика. Движение твердой среды
Теоретическая механика. Кинематика. Движение твердой среды Отражение и преломление света
Отражение и преломление света Сложение двух сил, направленных по одной прямой. Равнодействующая сил
Сложение двух сил, направленных по одной прямой. Равнодействующая сил Изучение процессов поглощения энергии при испарении жидкости и выделения ее при конденсации пара
Изучение процессов поглощения энергии при испарении жидкости и выделения ее при конденсации пара Решение задач на смеси
Решение задач на смеси Введение в волновую оптику. Энергия ЭМ волн. Вектор Пойнтинга. Лекция 2с 8 (1)
Введение в волновую оптику. Энергия ЭМ волн. Вектор Пойнтинга. Лекция 2с 8 (1) Балочные системы
Балочные системы Механическое движение
Механическое движение Устройство для наматывания нижней нити на шпульку
Устройство для наматывания нижней нити на шпульку Теплофизика процесса резания
Теплофизика процесса резания Электрическая диссоциация
Электрическая диссоциация Манометры
Манометры Презентация на тему Сейсмограф
Презентация на тему Сейсмограф  Устройство и принцип работы сцепления. Теоретическая подготовка водителей
Устройство и принцип работы сцепления. Теоретическая подготовка водителей Фізика прискорювачів
Фізика прискорювачів Электрические и магнитные дипольные моменты и энергия взаимодействия микрочастиц с внешним полем
Электрические и магнитные дипольные моменты и энергия взаимодействия микрочастиц с внешним полем Порядок действий при сборке конструкции/ механизма
Порядок действий при сборке конструкции/ механизма Использование простых механизмов
Использование простых механизмов