Содержание
- 4. При фиксированном m производящей функцией последовательности является
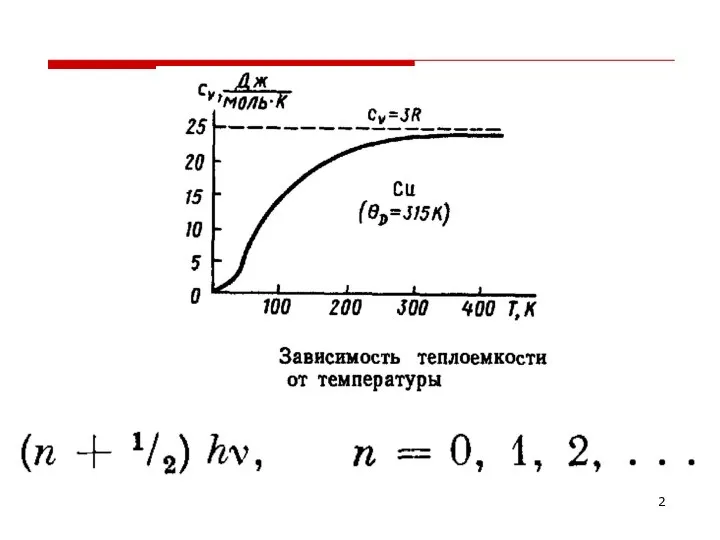
- 6. ТЕПЛОЕМКОСТЬ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- 7. ТЕПЛОЕМКОСТЬ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- 8. Θ- характеристическая температура Эйнштейна
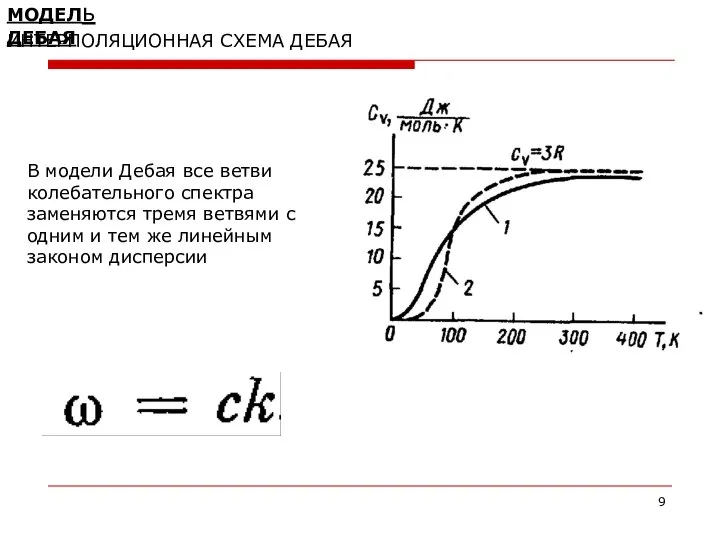
- 9. МОДЕЛь ДЕБАЯ ИНТЕРПОЛЯЦИОННАЯ СХЕМА ДЕБАЯ В модели Дебая все ветви колебательного спектра заменяются тремя ветвями с
- 10. 3rN-3 3
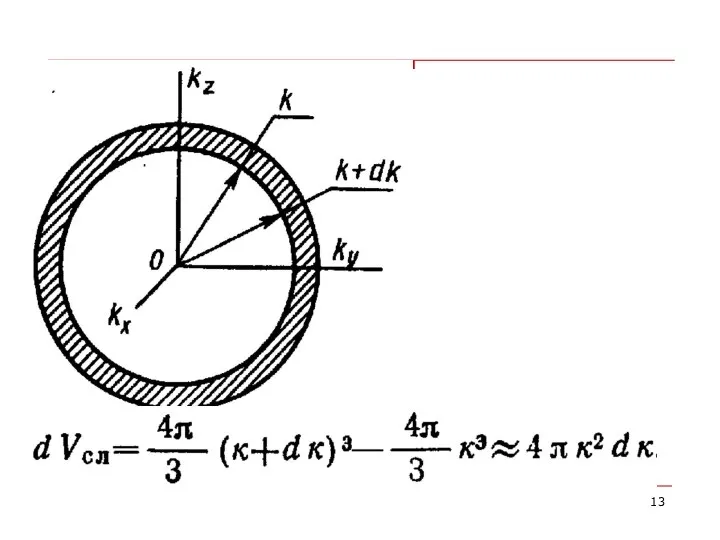
- 12. кристалла dN –число нормальных колебаний в интервале от k до k+dk Интегрирование производится по зоне Бриллюэна
- 15. Спектральная функция распределения частот Число нормальных колебаний в интервале ω − ω+dω
- 16. Усреднение по всем направлениям и типам колебаний
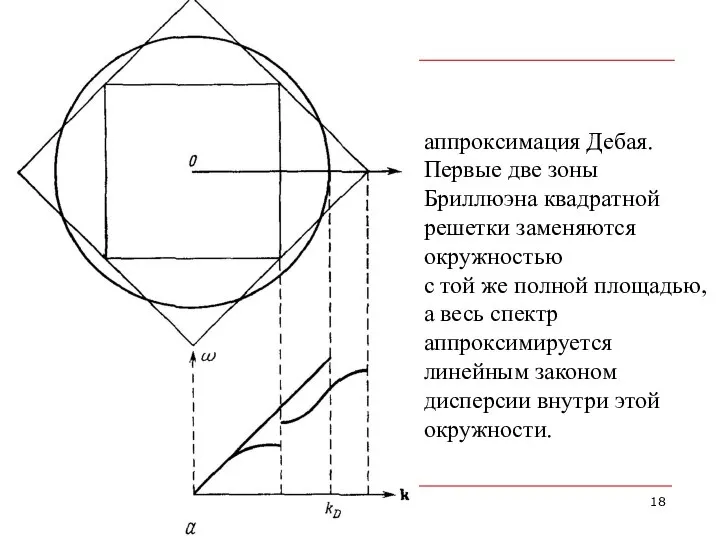
- 18. аппроксимация Дебая. Первые две зоны Бриллюэна квадратной решетки заменяются окружностью с той же полной площадью, а
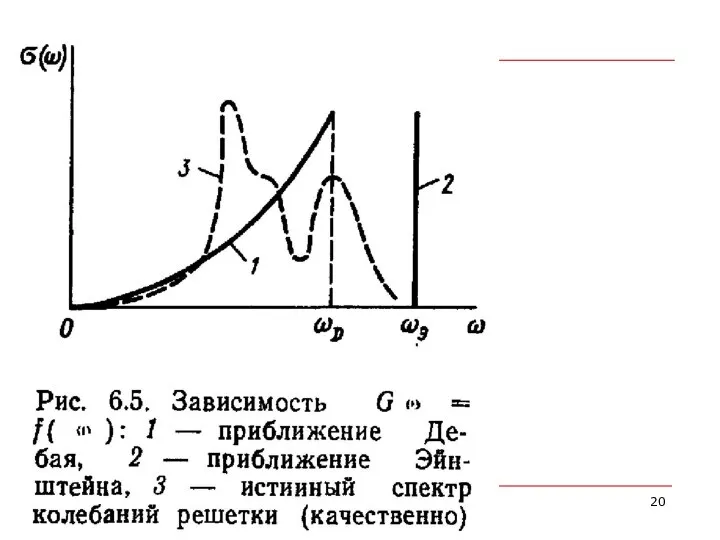
- 22. Интерполяционная формула Дебая
- 23. Функция Дебая ΘD/T максимальный квант энергии , способный возбудить колебания решетки выражает энергию = удельную теплоемкость
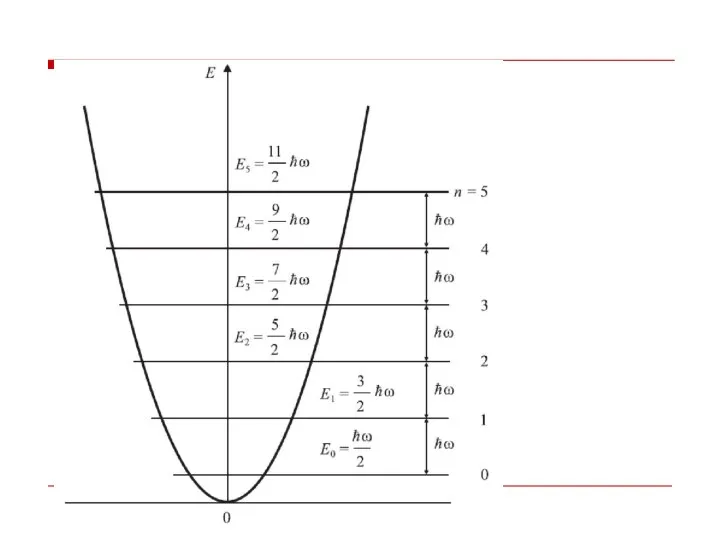
- 29. МОДЕЛЬ ЭЙНШТЕЙНА (еще раз)
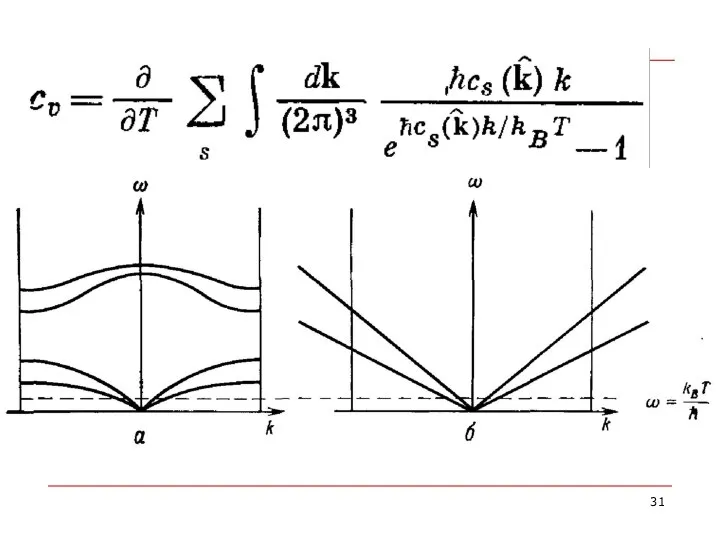
- 30. При очень низких температурах моды с частотами hωs(k) >> kвТ дают пренебрежимо малый вклад 1. Даже
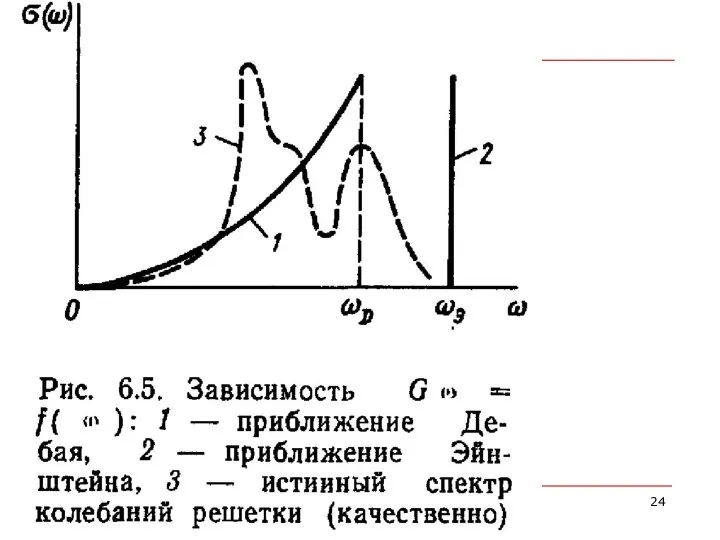
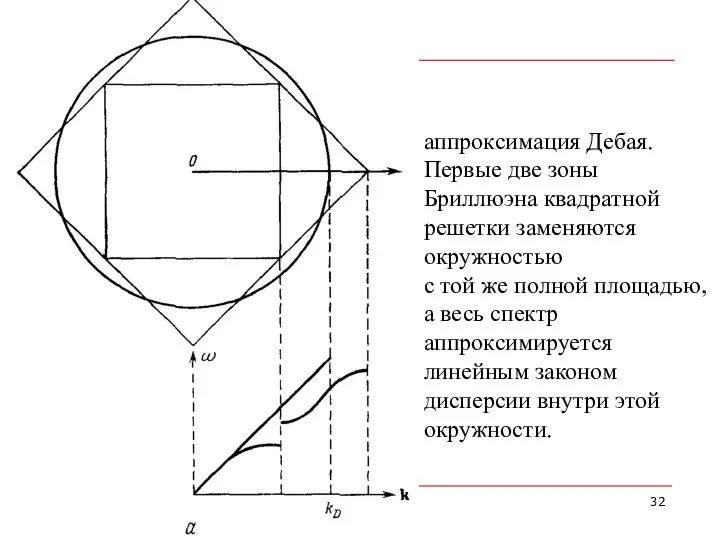
- 32. аппроксимация Дебая. Первые две зоны Бриллюэна квадратной решетки заменяются окружностью с той же полной площадью, а
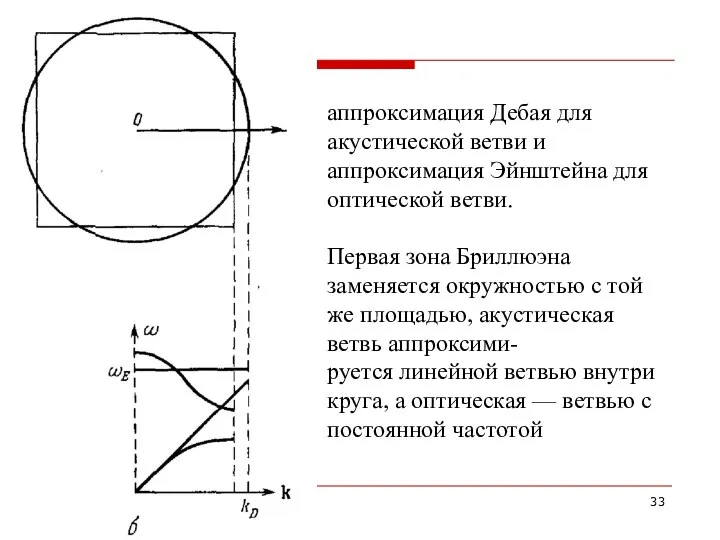
- 33. аппроксимация Дебая для акустической ветви и аппроксимация Эйнштейна для оптической ветви. Первая зона Бриллюэна заменяется окружностью
- 34. КВАНТОВАЯ ТЕОРИЯ ГАРМОНИЧЕСКОГО КРИСТАЛЛА Вывод формулы для теплоемкости, основанный на представлении о фононах
- 36. для плотности энергии гармонического кристалла
- 37. 2
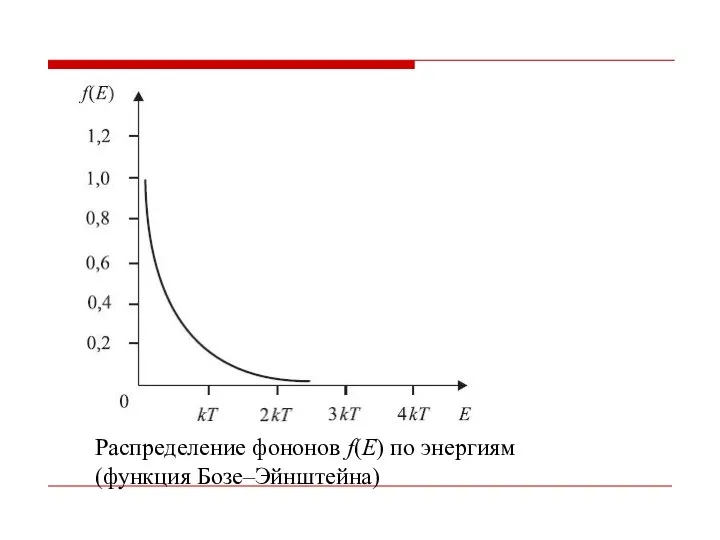
- 41. Распределение фононов f(E) по энергиям (функция Бозе–Эйнштейна)
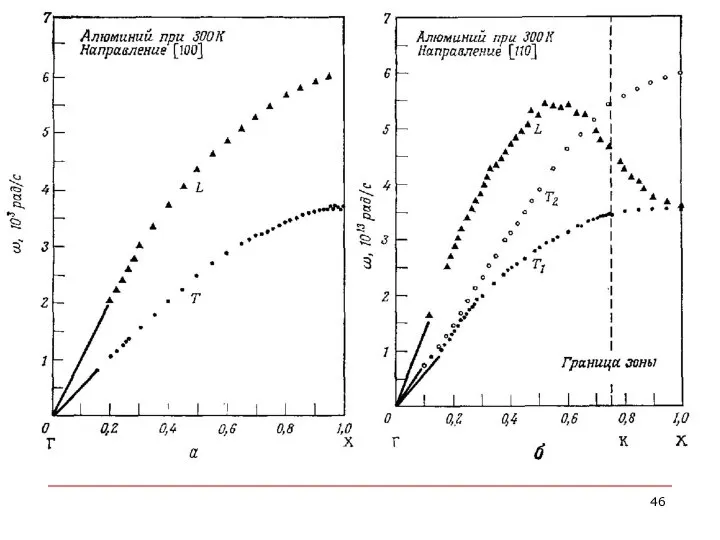
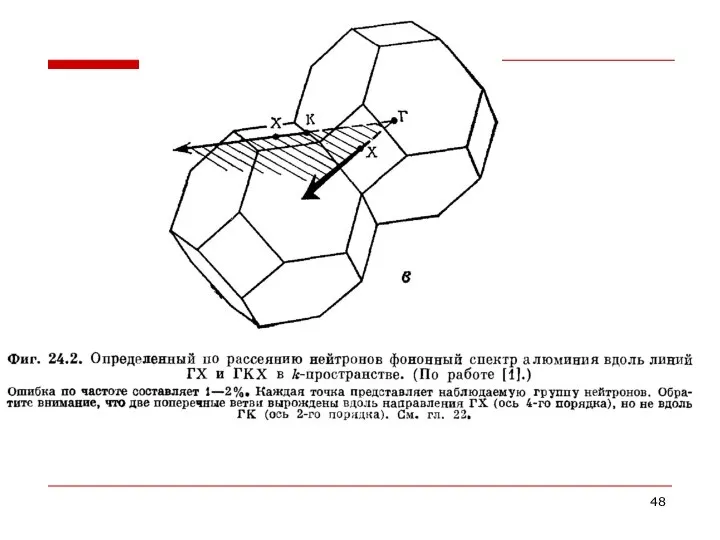
- 42. Исследования рассеяния нейтронов и фотонов представляют собой различные способы анализа фононного спектра - они характеризуются совершенно
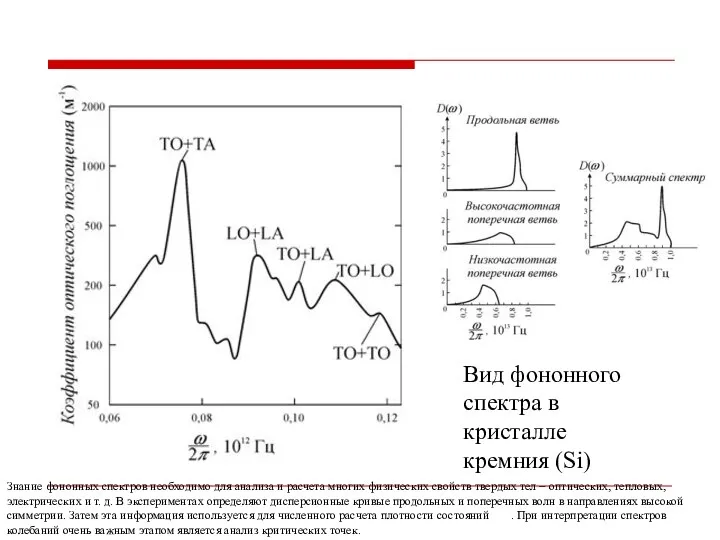
- 47. Вид фононного спектра в кристалле кремния (Si) Знание фононных спектров необходимо для анализа и расчета многих
- 49. 1/с3 — обратная третья степень длинноволновой фазовой скорости, усредненной по телесному углу и трем акустическим модам
- 51. Скачать презентацию







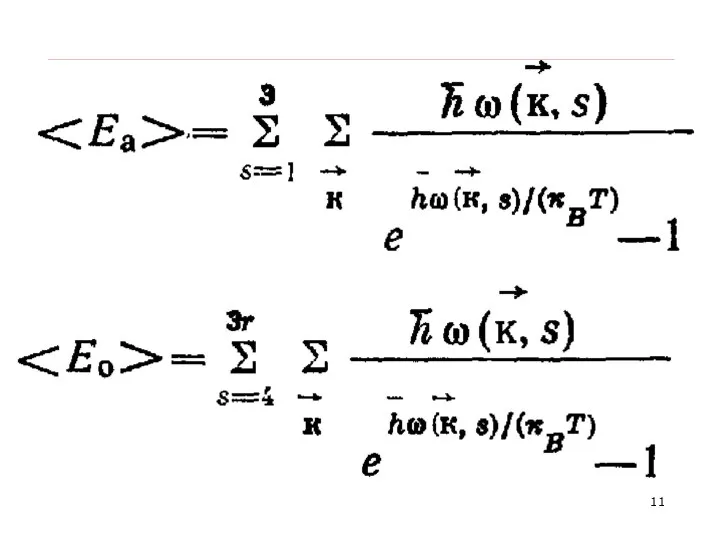


























 Классическая механика Ньютона
Классическая механика Ньютона Зарождение теории относительности
Зарождение теории относительности Явление электромагнитной индукции
Явление электромагнитной индукции Квантовые постулаты Бора
Квантовые постулаты Бора Энтропия. Употребление в различных дисциплинах
Энтропия. Употребление в различных дисциплинах Поглощенная доза излучения. Основы дозиметрии
Поглощенная доза излучения. Основы дозиметрии Дислокации. Механизмы размножения и движения дислокаций
Дислокации. Механизмы размножения и движения дислокаций Оценка параметров движения при зондировании последовательностью оптических импульсов
Оценка параметров движения при зондировании последовательностью оптических импульсов Линзы
Линзы Как мы знаем физику
Как мы знаем физику Стационарный режим работы однопоточного теплообменного аппарата
Стационарный режим работы однопоточного теплообменного аппарата Шпоночное соединение
Шпоночное соединение Электростатика. Электрический заряд. Электростатическое поле
Электростатика. Электрический заряд. Электростатическое поле Законы Ньютона
Законы Ньютона Деформация Сила упругости, закон Гука (Тема 1, Тема 2)
Деформация Сила упругости, закон Гука (Тема 1, Тема 2) Разработкой технологии дефектации прибора системы зажигания автомобиля ГАЗ-2752 Газель
Разработкой технологии дефектации прибора системы зажигания автомобиля ГАЗ-2752 Газель Электрический ток в полупроводниках
Электрический ток в полупроводниках Из истории радио
Из истории радио Нанотехнологии. Наноматериалы. Углеродные наноструктуры
Нанотехнологии. Наноматериалы. Углеродные наноструктуры Тест. Механические колебания
Тест. Механические колебания История создания конденсатора
История создания конденсатора Люминесцентные лампы
Люминесцентные лампы Статика
Статика Презентация на тему Распространение света
Презентация на тему Распространение света  Дифракция механических волн
Дифракция механических волн Импульс тела
Импульс тела Применение правила равновесия рычага к блоку. Золотое правило механики
Применение правила равновесия рычага к блоку. Золотое правило механики Расчетное сопротивление стали
Расчетное сопротивление стали