Гидравлические сопротивления. 4.1. Виды гидравлических сопротивлений

Для преодоления сопротивления трения и поддержания равномерного поступательного движения жидкости необходимо, чтобы на жидкость действовала сила, направленная в сторону ее движения и равная силе сопротивления, т.е. необходимо затрачивать энергию. Энергию или напор, необходимые для преодоления сил сопротивления, называют потерянной энергией или потерянным напором.
Потери напора, затрачиваемые на преодоление сопротивления трения, носят название потерь напора на трение или потерь напора по длине потока (линейные потери напора) и обозначаются через hтр.

Однако трение является не единственной возможной причиной, вызывающей потери напора; резкие изменения сечения также оказывают сопротивление движению жидкости (так называемое сопротивление формы) и вызывают потери энергии. Существуют и другие причины, вызывающие потери напора, например внезапное изменение направления движения жидкости. Потери напора, вызываемые резким изменением конфигурации границ потока (затрачиваемые на преодоление сопротивления формы), называют местными потерями напора или потерями напора на местные сопротивления и обозначают через hм.
Таким образом, потери напора при движении жидкости складываются из потерь напора на трение и потерь на местные сопротивления, т.е.
hω = hтр + hм

Режимы движения жидкостей. Критерий О. Рейнольдса
Наблюдения показывают, что в природе существуют два различных вида движения жидкости:
слоистое, упорядоченное или ламинарное движение, при котором отдельные слои жидкости скользят друг относительно друга, не смешиваясь между собой,
Ламинарный режим для воды и воздуха возможен лишь при их движении в трубах очень малого диаметра. Более вязкие жидкости, например масла, могут двигаться ламинарно даже в трубах значительного диаметра.
неупорядоченное, так называемое турбулентное движение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание.
Уже давно было известно, что вязкие жидкости (масла) движутся большей частью упорядоченно, а маловязкие жидкости (вода, воздух) почти всегда неупорядоченно.
Ясность в вопрос о том, как именно будет происходить движение жидкости в тех или иных условиях, была внесена в 1883 г. в результате опытов английского физика О. Рейнольдса.

О. Рейнольдс установил общие условия, при которых возможны существование ламинарного и турбулентного режима движения жидкости и переход от одного режима к другому. Оказалось, что состояние (режим) потока жидкости в трубе зависит от величины безразмерного числа, которое учитывает основные факторы, определяющие это движение: среднюю скорость v, диаметр трубы d, плотность жидкости ρ и ее абсолютную вязкость μ. Это число (позже ему было присвоено название числа Рейнольдса) имеет вид:

Величина d в числе Рейнольдса может быть заменена любым линейным параметром, связанным с условиями течения или обтекания (диаметр трубы, диаметр падающего в жидкости шара, длина обтекаемой жидкостью пластинки и др.).
Значение числа Рейнольдса, при котором происходит переход от ламинарного движения к турбулентному, называют критическим числом Рейнольдса и обозначают Rекр.

При Rе > Rекр режим движения является турбулентным,
при Rе < Rекр – ламинарным.
Величина критического числа Рейнольдса зависит от условий входа в трубу, шероховатости ее стенок, отсутствия или наличия первоначальных возмущений в жидкости, конвекционных токов и др.

Вопрос о неустойчивости ламинарного движения и его переходе в турбулентное, а также о величине критического числа Рейнольдса подвергся тщательному теоретическому и экспериментальному изучению, но до сих пор еще уточняется. Наиболее часто в расчетах принимают для критического числа Рейнольдса значение
Rекр = 2300,
отвечающее переходу движения жидкости из турбулентного в ламинарное;
при переходе движения из ламинарного в турбулентное критическое число Рейнольдса имеет большую величину (для хорошо закругленного плавного входа оно может быть доведено до 20 000).

Проведенные исследования показывают также, что критическое значение числа Рейнольдса увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах усиливается.
По критическому значению числа Рейнольдса легко можно найти также критическую скорость, т.е. скорость, ниже которой всегда будет иметь место ламинарное движения жидкости:

Общее выражение для потерь напора на трение
при равномерном движении жидкости в трубах
Найдем общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов.
Рассмотрим равномерное течение жидкости в трубе постоянного диаметра. Выделим два сечения 1 и 2. Потерю напора между этими сечениями определим из уравнения Бернулли:
Из этого уравнения найдем величину потерянной энергии hтр
Выражение называют уравнением равномерного движения жидкости в трубопроводах.

Турбулентное равномерное движение жидкости в трубах.
При равномерном движении в трубах потери напора на трение по длине hл как при турбулентном, так и при ламинарном движении определяют для круглых труб по формуле Дарси-Вейсбаха:
для труб любой формы сечения по формуле
где λ – коэффициент гидравлического трения (безразмерный)

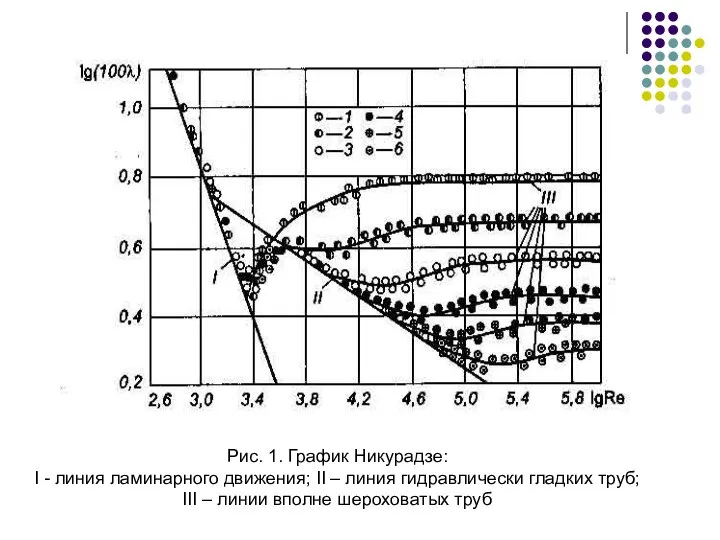
Рис. 1. График Никурадзе:
I - линия ламинарного движения; II – линия гидравлически гладких труб; III – линии вполне шероховатых труб

Трубы, в которых коэффициент гидравличес-
кого трения λ не зависит от вязкости жидкости (числа Рейнольдса), а зависит только от относительной шероховатости, называют вполне шероховатыми.
Трубы же, в которых коэффициент λ вовсе не зависит от шероховатости стенок, а зависит только от числа Рейнольдса, называют гидравлически гладкими.
Из графика Никурадзе видно, что одна и та же труба в одних условиях может быть гидравлически гладкой, а в других – вполне шероховатой.
Область движения, в которой λ зависит и от Rе, и от k/d, называют переходной (область смешанного трения).

Полученным результатам можно дать следующее физическое истолкование.
При малых числах Рейнольдса жидкость обтекает выступы шероховатости без образования и отрыва вихрей благодаря значительному влиянию вязкости жидкости; свойства поверхности стенок труб не оказывают при этом влияния на сопротивление и кривые λ = f (Rе) совпадают с прямой II (для гладких труб). Когда же с увеличением скорости (т.е. числа Рейнольдса) от бугорков шероховатости начинают отрываться вихри, то свойства поверхности уже оказывают влияние на сопротивление и кривые λ = f (Rе) отклоняются от линии гладкого трения.

В результате опытов сопротивлений трубопроводов были предложены различные эмпирические формулы для определения коэффициента гидравлического трения λ.
Для гидравлически гладких труб широкое распространение получила формула Блазиуса

Для полиэтиленовых водопроводных труб, обычно работающих в области гидравлически гладких труб, применяют формулу Ф.А. Шевелева
Для вполне шероховатых труб применяют формулу Б.Л. Шифринсона:

Ламинарное течение. При ламинарном течении в круглых трубах коэффициент гидравлического трения вычисляют по формуле
λ = 64 / Rе
для труб любой формы сечения –
λ = А / Rе
где А – коэффициент, численное значение которого зависит от формы поперечного сечения трубы.

число Рейнольдса дляламинарного режима определяется по формуле
где
Значения коэффициента формы А и эквивалентного диаметра dэ для труб с различной формой поперечного сечения справочные данные.
зависимость для определения потерь напора по длине при ламинарном движении в круглых трубах в виде
Эта формула получила название формулы Пуазейля

Местные гидравлические сопротивления
Местные потери напора обусловливаются преодолением местных сопротивлений, создаваемых фасонными частями, арматурой и прочим оборудованием трубопроводных сетей. Местные сопротивления вызывают изменение величины или направления скорости движения жидкости на отдельных участках трубопровода, что связано с появлением дополнительных потерь напора. Движение в трубопроводе при наличии местных сопротивлений является неравномерным. Потери напора в местных сопротивлениях hм (местные потери напора) вычисляют по формуле Вейсбаха:
где v – средняя скорость в сечении, как правило, расположенном ниже по течению за данным сопротивлением;
ζ – безразмерный коэффициент местного сопротивления.

Потери давления Δрм:
Значения коэффициентов местных сопротивлений зависят от конфигурации местного сопротивления и режима потока, подходящего к сопротивлению; этот режим определяется коэффициентом гидравлического трения λ подходящего потока, т.е. числом Рейнольдса и относительной шероховатостью.

Внезапное расширение трубопровода
Потери напора при внезапном расширении трубопровода находят по формуле Борда:
где v1 и v2 – средние скорости течения соответственно до и после расширения.
Коэффициенты местного сопротивления определяются выражениями (справочные даны):
где ω1 и ω2 – площади сечений трубопровода соответственно до и после расширения.

Внезапное сужение трубопровода
Коэффициент местного сопротивления при внезапном сужении
где ε – коэффициент сжатия струи, представляющий собой отношение площади сечения сжатой струи в узком трубопроводе ωсж к площади сечения узкой трубы ω2
ε = ωсж / ω2
Коэффициент сжатия струи ε зависит от степени сжатия потока n = ω2 / ω1
и может быть найден по формуле А.Д. Альтшуля:

Диафрагма на трубопроводе
Коэффициент местного сопротивления диафрагмы, расположенной внутри трубы постоянного сечения (отнесенный к сечению трубопровода),
где nдиафр = ω0 / ω – отношение площади отверстия диафрагмы ω0 к площади сечения трубы ω
Для диафрагмы, расположенной на выходе в трубопровод другого диаметра, коэффициент сопротивления, отнесенный к сечению узкого трубопровода
где m = ω2 / ω1 , nдиафр = ω0 / ω1

Вход в трубу из резервуара
Для коэффициента сопротивления следует принимать следующие значения:
при острых кромках ξвх = 0,4 – 0,5;
при закругленных кромках ξвх = 0,2;
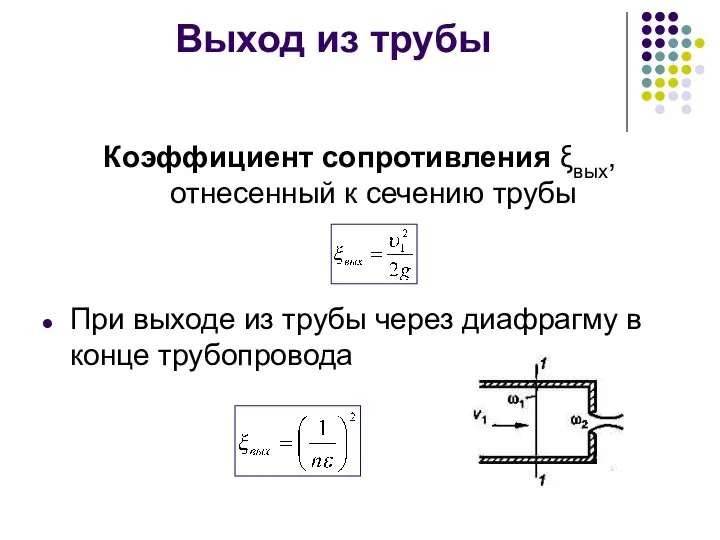
при весьма плавном входе ξвх = 0,05.

Выход из трубы
Коэффициент сопротивления ξвых, отнесенный к сечению трубы
При выходе из трубы через диафрагму в конце трубопровода

Сварные стыки на трубопроводах
Коэффициент сопротивления стыка определяется как:
где δ – эквивалентная высота сварного стыка:
для стыков с подкладными кольцами δ = 5 мм;
для стыков электродуговой и контактной сварки δ = 3 мм.
Возрастание сопротивления, вызываемое стыками, можно определить по формуле
где К = λ1 / λ – относительное увеличение сопротивления трубопровода (отношение сопротивления трубопровода со стыками к сопротивлению трубопровода без стыков);
l – расстояние между стыками (длина труб).

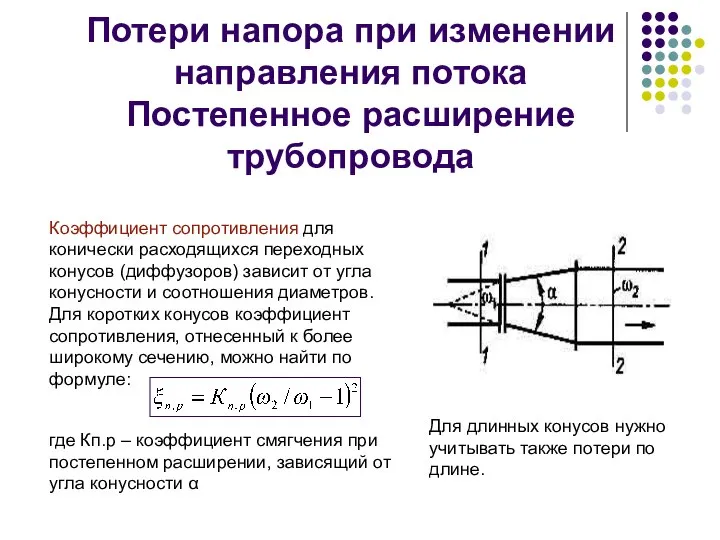
Потери напора при изменении направления потока
Постепенное расширение трубопровода
Коэффициент сопротивления для конически расходящихся переходных конусов (диффузоров) зависит от угла конусности и соотношения диаметров. Для коротких конусов коэффициент сопротивления, отнесенный к более широкому сечению, можно найти по формуле:
где Кп.р – коэффициент смягчения при постепенном расширении, зависящий от угла конусности α
Для длинных конусов нужно учитывать также потери по длине.

Постепенное сужение трубопровода
Коэффициент сопротивления для сходящихся переходных конусов (конфузоров) зависит от угла конусности и соотношения диаметров.
Для коротких конусов
где Кпс – коэффициент смягчения при постепенном сужении, зависящий от угла конусности α;

Резкий поворот трубы круглого поперечного сечения на угол α.
Коэффициент сопротивления можно найти по формуле:
где ξ90 – значение коэффициента сопротивления для угла 90˚

Плавный поворот трубы круглого поперечного сечения (закругленное колено, отвод).
Коэффициент сопротивления
Коэффициент ξ90 определяется по формуле А.Д. Альтшуля:
где d – диаметр трубопровода;
R – радиус закругления.

Потери напора в запорных устройствах трубопроводов
Теоретические значения коэффициента сопротивления для задвижки
где ω0 – площадь сечения, не стесненная запорным приспособлением;
ω – площадь сечения трубы.
Значения коэффициентов местных сопротивлений для некоторых запорных устройств (задвижка, вентиль, дроссель, кран и др.) приведены в справочных данных.

Местные потери в трубах при малых числах Рейнольдса
Приведенные выше формулы относятся к турбулентному течению с большими числами Рейнольдса, когда влияние вязкости жидкости проявляет себя лишь в слабой степени.
При движении жидкости с малыми числами Рейнольдса коэффициенты местных сопротивлений зависят не только от геометрических характеристик сопротивления, но и от числа Рейнольдса и могут быть при ориентировочных расчетах найдены по формуле А.Д. Альтшуля:
где ξкв – значение коэффициента местного сопротивления в квадратичной области;
Rе – число Рейнольдса, отнесенное к нестесненному сечению трубопровода.
Значения параметров А и ξкв для местных сопротивлений табличные значения.

Задачи
1. Горизонтальная труба диаметром d1 = 0,1 м внезапно переходит в трубу диаметром d2 = 0,15 м. Проходящий расход воды Q = 0,03 м3/с.
Требуется определить:
а) потери напора при внезапном расширении трубы; б) разность давлений в обеих трубах;
в) потери напора и разность давлений для случая, когда вода будет течь в противоположном направлении (т.е. из широкой трубы в узкую);
г) разность давлений при постепенном расширении трубы (считая потери напора пренебрежимо малыми).