Теплофизика процесса резания

Физическая модель. Балансовые соотношения
Лекция 1
Суть процессов, происходящих в зоне механической обработки детали очень сложна.
• Во-первых, потому, что происходит превращение одних видов энергии в другие (механической в потенциальную энергию кристаллической решетки и тепловую вследствие наличия трения).
• Во-вторых, потому что слишком большое количество факторов оказывает влияние на результирующую картину (теплофизические свойства материала заготовки и инструмента, параметры механической обработки (скорость, подача, глубина и др.), состояние материала в поверхностном слое заготовки, наличие или отсутствие влияния технологических сред или других источников воздействия на зону механической обработки).

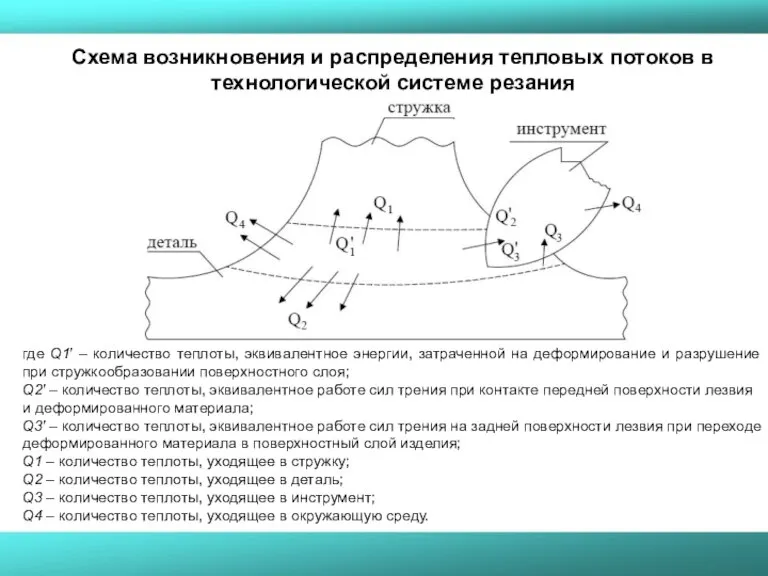
где Q1′ – количество теплоты, эквивалентное энергии, затраченной на деформирование и разрушение при стружкообразовании поверхностного слоя;
Q2′ – количество теплоты, эквивалентное работе сил трения при контакте передней поверхности лезвия и деформированного материала;
Q3′ – количество теплоты, эквивалентное работе сил трения на задней поверхности лезвия при переходе деформированного материала в поверхностный слой изделия;
Q1 – количество теплоты, уходящее в стружку;
Q2 – количество теплоты, уходящее в деталь;
Q3 – количество теплоты, уходящее в инструмент;
Q4 – количество теплоты, уходящее в окружающую среду.
Схема возникновения и распределения тепловых потоков в технологической системе резания

Теплоотдача, под которой понимают конвективный теплообмен между потоком жидкости или газа и поверхностью твердого тела. Этот процесс чаще всего описывают уравнением Ньютона-Рихмана:
Q = α ⋅ F ⋅ (tж – tт)
где F – поверхность теплоотдачи, м2;
tж, tт – температуры жидкости и тела, К или °С;
α – коэффициент теплоотдачи, Вт/(м2⋅К).
α = Q / F ⋅ (tж - tт).
Коэффициент теплоотдачи α представляет собой количество тепла, отдаваемое или воспринимаемое единицей поверхности теплоотдачи F при разности температур между жидкостью и стенкой 1К. Коэффициент теплоотдачи α зависит от большого числа факторов:
формы и размеров тела, режима движения, скорости и температуры жидкости, ее теплофизических свойств и т. п.

Факторы, влияющие на величину коэффициента теплоотдачи
Влияние скорости потока v. С увеличением скорости потока жидкости или газа толщина пограничного слоя δ уменьшается, следовательно, α. возрастает.
Влияние вязкости μ. Чем выше вязкость, тем больше касательные силы вязкого трения, тем толще оказывается пограничный слой. Это должно приводить к уменьшению α. Снижение интенсивности теплоотдачи обусловлено также ухудшением перемешивания с ростом вязкости.
Влияние плотности ρ. Уменьшение плотности влечет за собой рост
толщины пограничного слоя, следовательно, снижение коэффициента теплоотдачи. К этому следует добавить, что теплота, переносимая единицей объема пропорциональна плотности, что усиливает влияние плотности на интенсивность теплоотдачи.
Коэффициент теплопроводности λ находится в прямой связи с коэффициентом теплоотдачи. С ростом λ растет и α.

Тепловое излучение – это процесс распространения тепловой энергии с помощью электромагнитных волн. При тепловом излучении происходит двойное превращение энергии: тепловая энергия излучающего тела переходит в лучистую и, наоборот, лучистая энергия, поглощаясь телом, переходит в тепловую.
При данной температуре наибольший тепловой поток излучает абсолютно черное тело. Величина его плотности определяется законом Стефана-Больцмана:
q = σ0 ⋅ T 4,
где σ0 = 5,67⋅10-8 Вт/(м2⋅ К4) – константа излучения абсолютно черного тела.
Плотность теплового потока, излучаемого нечерными телами, оценивается формулой:
q = ε ⋅ σ0 ⋅ T 4,
где ε – степень черноты. Ее величина 0 < ε < 1 и определяется экспериментально или из справочника.

При лучистом теплообмене между двумя телами они одновременно облучают друг друга. Результирующая теплота, переданная излучением
от тела с более высокой температурой к телу с более низкой, определяется выражением:
Q12 = σпр. ⋅ F ⋅ (T1 4 – T2 4),
где F – взаимная поверхность облучения, м2; σпр – приведенная константа излучения, Вт/(м2⋅ К4); T1, T2 – температура тел, К.
Тепловой поток – количество теплоты, которое передается в единицу времени от источника теплоты к какому-либо телу (стоку). Тепловой поток (Q) измеряется в Вт, кВт и т.п.
Плотность (интенсивность) теплового потока – тепловой поток, отнесенный к единице поверхности, объема или длины теплового источника. Плотность теплового потока обозначается q:
q =, Q/F ⋅ (V , L )
где F – площадь передачи теплоты, перпендикулярная направлению теплового потока, м2; V – объем, м3; L – длина, м.

Источником называется объект, генерирующий теплоту.
Мощность источника оценивается величиной генерируемого теплового потока или его плотностью.
Стоком называется объект, поглощающий теплоту.
Температурное поле – совокупность значений температуры тела в любой момент времени. Его наиболее общее математическое выражение:
t = t ⋅ (x, y, z, τ),
где x, y, z – координаты отдельной точки тела; τ – время.

Изотермические поверхности – геометрическое место точек, имеющих одинаковую температуру. Изотермические поверхности не могут пересекаться друг с другом. Они или замыкаются сами на себя, или обрываются на границах тела.
Изотермические линии (изотермы) – линии, образованные пересечением изотермических поверхностей с секущей плоскостью. Как и изотермические поверхности, изотермические линии не могут пересекаться друг с другом – они или замыкаются сами на себя, или обрываются на границах тела.
Температурный градиент – предел отношения изменения температуры между двумя изотермами к расстоянию между последними, измеренному по нормали.
Температурный градиент векторная величина. Его положительное направление совпадает с направлением роста температуры.
Лекция 2

Основной закон теплопроводности
Рассмотрим элемент изотермической поверхности dF. По нормали n покажем вектор grad t. Следовательно, поток теплоты, который представим в виде вектора dQ, направлен в противоположную сторону.
где λ – коэффициент теплопроводности, Вт/(м⋅К).
В 1882 году Ж-Б-Фурье высказал гипотезу о том, что количество теплоты dQ, проходящее через элемент поверхности dF за время dτ пропорционально grad t
Отношение плотности теплового потока:
представляющее собой количество теплоты, проходящее в единицу времени, через единицу площади изотермической поверхности есть не что иное, как плотность теплового потока.

Подставляя выражения получим:
где q – вектор плотности (интенсивности) теплового потока.
Коэффициент теплопроводности – это теплота, передаваемая теплопроводностью в единицу времени через единицу поверхности при перепаде температуры на единицу длины нормали, равном одному градусу, размерность его - Вт/(м⋅К).
Коэффициент теплопроводности λ характеризует физические свойства материала.

Дифференциальное уравнение теплопроводности
Математическое описание температурных полей в компонентах технологических систем выполняется с помощью дифференциального уравнения теплопроводности.
Выделим из нагреваемого тела элементарный объем ΔV,
где ΔV = Δx ⋅ Δy ⋅ Δz.
На основании закона изменения внутренней энергии
dU= dQ1+ dQ2 ,
где dU – общее изменение внутренней энергии вещества в объеме ΔV за время Δτ;
dQ1 – количество теплоты, поступившее в этот объем путем теплопроводности;
dQ2 – количество теплоты, возникшее в объеме ΔV в связи с функционированием в нем внутренних источников.
К внутренним относятся источники, тепловыделение которых связано с процессами, происходящими в материале твердого тела, например, с объемными химическими реакциями, действием электрического тока и т. д.

Элементарные количества теплоты dQ1 и dQ2 вызовут изменение температуры вещества и величину dU можно найти из уравнения:
где с – массовая теплоемкость, Дж/(кг⋅К),
ρ – плотность вещества, кг/ м3.
Таким образом, в наиболее простом виде дифференциальное уравнение теплопроводности выглядит так:
где ∇2 – оператор Лапласа.
λ/c ⋅ ρ = а – коэффициент температуропроводности данного вещества.

Классификация источников
1. Расположение и форма источников
По расположению источники теплоты можно разделить на внешние, действующие на поверхности тел, и внутренние, функционирующие в их массе
Лекция 3
где М – мерность: К – конфигурация: О – ограниченность источника теплоты; Р – закон распределения источника; С – его скорость;
Д – длительность функционирования; Т – форма тела, на котором действует источник; У – род граничных условий.

2. Закон распределения интенсивности источника
Классификация источников
Закон распределения интенсивности (плотности теплового потока) является одной из важнейших характеристик источника.
Чтобы для каждого из них установить тепловую мощность, необходимо:
1) определить общую тепловую мощность процесса;
2) распределить последнюю между конкретными источниками, возникающими в данной технологической операции, то есть составить приходную часть теплового баланса.
а. Самым простым является равномерное стационарное распределение, когда интенсивность q0 не зависит от координат и времени.
б. Следующую группу представляют источники с линейно распределенной интенсивностью.
Из условий q (ℓ, 0, z) = 0 и q (x, Δ, z) = 0 получаем:

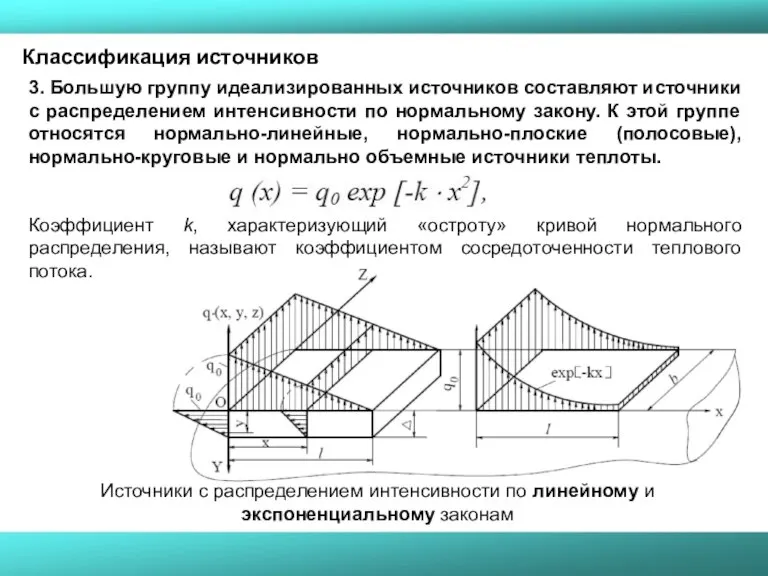
3. Большую группу идеализированных источников составляют источники с распределением интенсивности по нормальному закону. К этой группе относятся нормально-линейные, нормально-плоские (полосовые), нормально-круговые и нормально объемные источники теплоты.
Классификация источников
Коэффициент k, характеризующий «остроту» кривой нормального распределения, называют коэффициентом сосредоточенности теплового потока.
Источники с распределением интенсивности по линейному и экспоненциальному законам

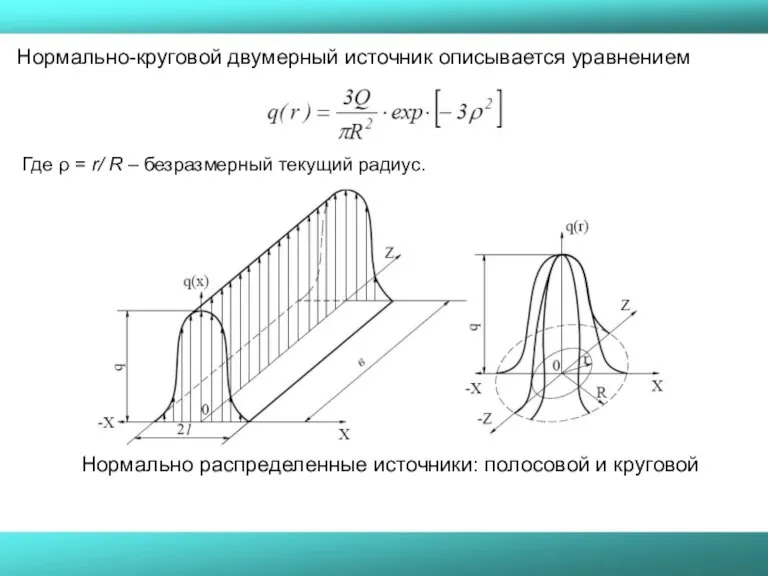
Нормально-круговой двумерный источник описывается уравнением
Где ρ = r/ R – безразмерный текущий радиус.
Нормально распределенные источники: полосовой и круговой

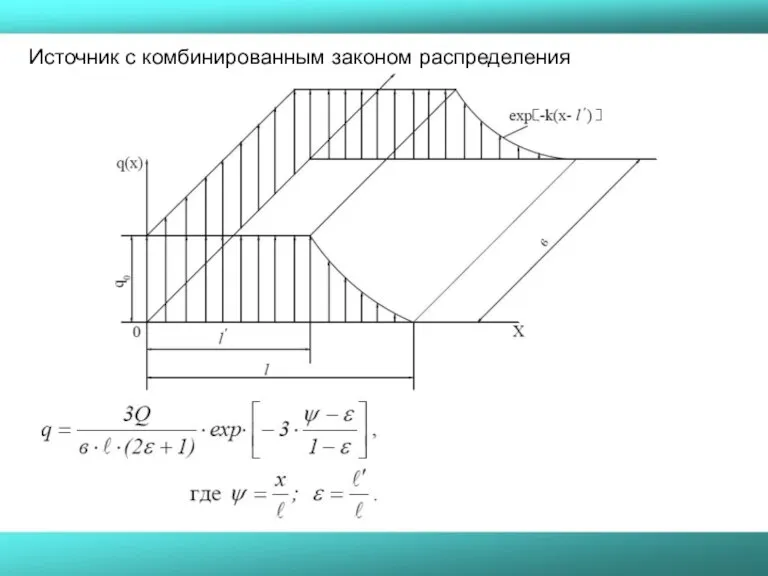
Источник с комбинированным законом распределения

Скорость перемещения и длительность функционирования источника
Классификация источников
Скорость перемещения источников в теплофизических расчетах обычно характеризуют безразмерным критерием Пекле
где v – скорость движения источника; ℓ – характерный линейный размер;
а – коэффициент температуропроводности.
Если Рe = 0 – источник – неподвижный, если Рe ≥ 10, то источник быстродвижущийся; при 0 < Рe < 10 – источник движется со средней скоростью.
По времени функционирования источники можно разделить на:
1) мгновенные;
2) действующие в течение конечного промежутка времени;
3) действующие периодически;
4) действующие столь длительное время, что процесс теплообмена
можно считать стационарным.

Лекция 4
Общие принципы схематизации тел и источников, участвующих
в теплообмене при механической обработке материалов
Допустимость той или иной идеализации формы реальных тел определяется:
1) соотношением между размерами площадок, занимаемых источниками теплоты, и размерами нагреваемого тела;
2) временем от начала процесса теплообмена до момента времени,
для которого рассчитывают температуры;
3) наличием пассивных граничных поверхностей;
4) требуемой точностью расчета.
Чем меньше размеры источника по отношению к размерам нагреваемого тела, тем меньше влияние конкретной формы тела на температурное поле в области, прилежащей к источнику.

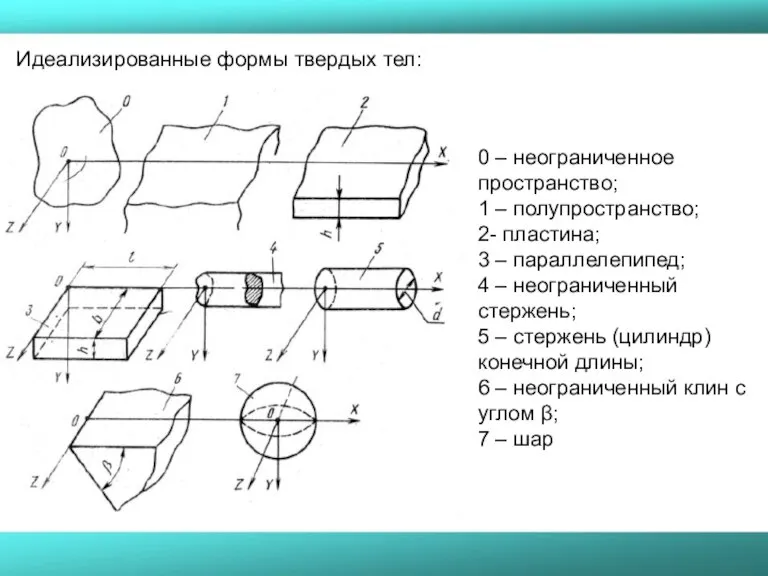
Идеализированные формы твердых тел:
0 – неограниченное пространство;
1 – полупространство;
2- пластина;
3 – параллелепипед;
4 – неограниченный стержень;
5 – стержень (цилиндр) конечной длины;
6 – неограниченный клин с углом β;
7 – шар

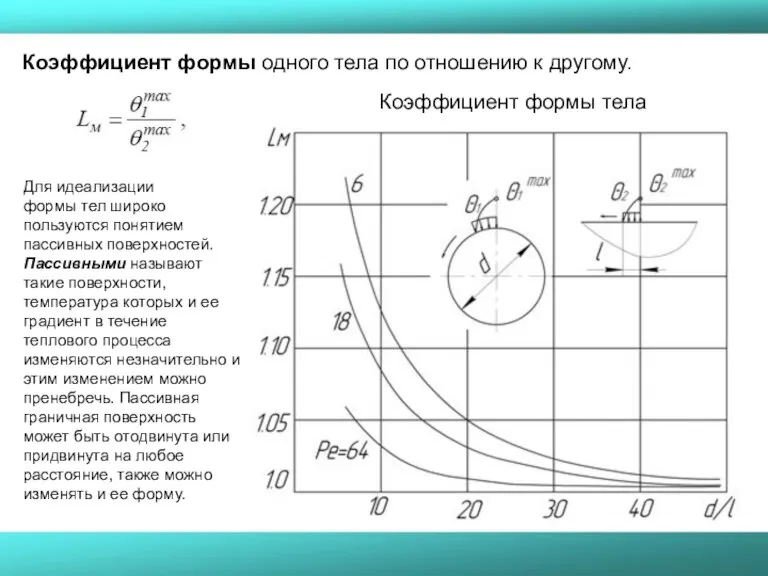
Коэффициент формы одного тела по отношению к другому.
Коэффициент формы тела
Для идеализации
формы тел широко пользуются понятием пассивных поверхностей.
Пассивными называют такие поверхности, температура которых и ее
градиент в течение теплового процесса изменяются незначительно и этим изменением можно пренебречь. Пассивная граничная поверхность может быть отодвинута или придвинута на любое расстояние, также можно изменять и ее форму.

Лекция 5
Расчет температуры в зоне резания
Теплота в процессе резания определяется:
внутренним трением между частицами обрабатываемого металла в процессе деформации;
внешним трением стружки о переднюю поверхность резца;
внешним трением обработанной поверхности о заднюю поверхность резца;
смазочно-охлаждающей жидкостью.
где То – начальная температура (температура окружающей среды), То = 20 – 28 С°;
Тε – температура в плоскости сдвига, С°;
Тп.п – температура на передней поверхности, С°;
Тз.п – температура на задней поверхности, С°;
ТСОЖ – температура от смазочно-охлаждающей жидкости, С°;
Тстр – температура стружки, С°.
Лекция

Температура в плоскости сдвига
где SВ – действительный предел прочности обрабатываемого материала при растяжении –
SВ = 0,95 · (1 + δ),
где δ – относительное удлинение;
CV – удельная объемная теплопроводность, Дж/м3·С°;
ε – относительный сдвиг, ε = (1 + 1/K – 2 · sinγ) / cosγ,
где γ – передний угол резца;
К – коэффициент усадки стружки,
K = cos(β – γ) / sinβ,
где β – угол режущего клина резца;
β = 90° - (γ + α), где α – задний угол резца.
Расчетная схема резания

где с – длина контакта стружки по передней поверхности резца, в общем случае
с = (1 - 2) · а; V – скорость резания, м/с; а – толщина срезаемого слоя, мм;
h – износ по задней поверхности, мм; ω – коэффициент температуропроводности, мм2/с.
Температура на передней поверхности
Температура на задней поверхности
где σВ – предел прочности обрабатываемого материала на разрыв, МПа; h – износ по задней поверхности, мм.

Температура от СОЖ
где t – глубина резания, мм; S – подача, мм/об; G – расход СОЖ, л/мин;
T1 – начальная температура СОЖ, С°; в общем случае T1 = To;
T2 – конечная температура СОЖ, С°; в общем случае T2 = To + Tε + Tп.п + Tз.п;
ССОЖ – удельная теплоёмкость СОЖ, кДж/кг·С°; ρСОЖ – плотность СОЖ, кг/м3;
Fсоп – площадь сопла, мм2.
где α0 – коэффициент, учитывающий потерю теплоты на скрытую энергию деформации (принимаем α0 = 0,95); β0 – коэффициент, учитывающий переход части тепла в изделие (по Вейнеру: β0 = 0,1 при V = 100 м/мин, β0 = 0,05 при V = 300 м/мин); μ0 – коэффициент трения стружки; ξ – коэффициент усадки стружки; с – теплоёмкость нагретой стружки, ккал/кгс·°С; ρстр – плотность стружки, кгс/мм3; а – толщина среза, мм; b – ширина среза, мм; Е – модуль упругости материала стружки, кгс/мм2; P = Pz/a·b – удельная сила резания, кгс/мм2;

При расчете температуры в зоне резания при обработке ст. 45 (σВ = 600 МПа; δ = 0,3; CV = 6,11 Дж/м3·С°; ω = 31 мм2/с), резцом (γ = 10°; β = 70°; α = 10°), при режимах V = 400 м/мин; t = 2 мм; S = 0,25 мм/об; с применением СОЖ G = 50 л/мин; T1 = Tо = 20°; ССОЖ = 4,184 Дж/кг·С°; ρСОЖ = 998 кг/м3; Fсоп = 78,5 мм2; h = 0,1 мм получено значение – 185,8 °С, реально полученные значения находятся в диапазоне – 170-200 °С. Рассчитанная температура в зоне резания ст. 45 без применения СОЖ имеет значение 590,1 °С, реально полученные значения находятся в диапазоне – 570-610 °С.

Тепловые явления
Виды температур
1. Мгновенная контактная температура непосредственно в зоне контакта рабочей части режущего инструмента и обрабатываемой поверхности. Эта температура наиболее высокая и может достигать температуры плавления материала детали, о чем свидетельствуют исследования. 1000 – 1300 °С
2. Контактная температура образуется непосредственно в зоне контакта режущего инструмента с заготовкой. Данная температура является результатом суммарного теплового воздействия режущего клина и теплоотвода в тело детали и окружающую среду. 600 – 800 °С
3. Средняя температура нагрева всей обрабатываемой поверхности заготовки обычно составляет 50 – 150 °С. Эта температура определяет тепловые деформации и, таким образом, влияет на геометрическую точность обрабатываемой детали.
Эмпирические зависимости расчет температуры
Лекция 6

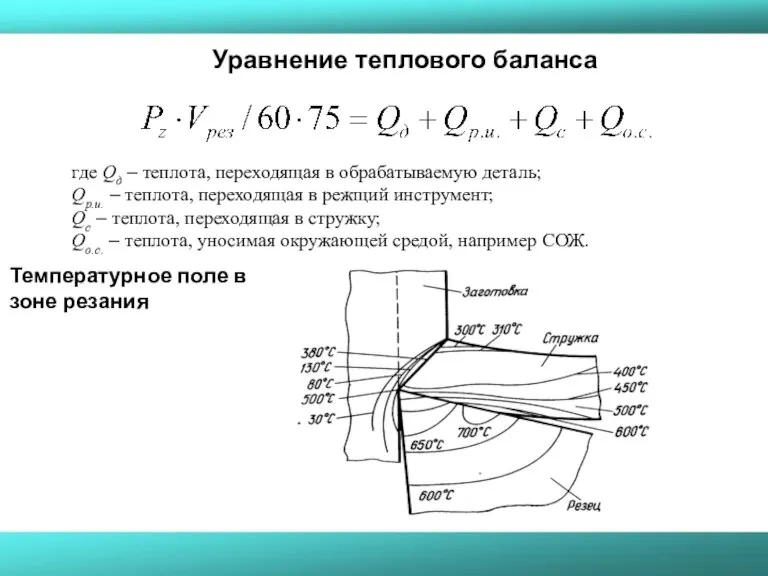
Уравнение теплового баланса
где Qд – теплота, переходящая в обрабатываемую деталь;
Qр.и. – теплота, переходящая в режщий инструмент;
Qс – теплота, переходящая в стружку;
Qо.с. – теплота, уносимая окружающей средой, например СОЖ.
Температурное поле в зоне резания

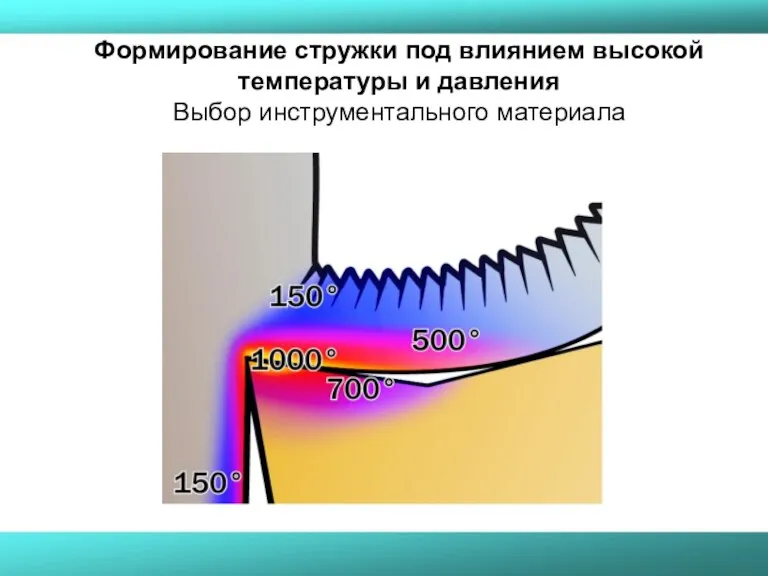
Формирование стружки под влиянием высокой температуры и давления
Выбор инструментального материала

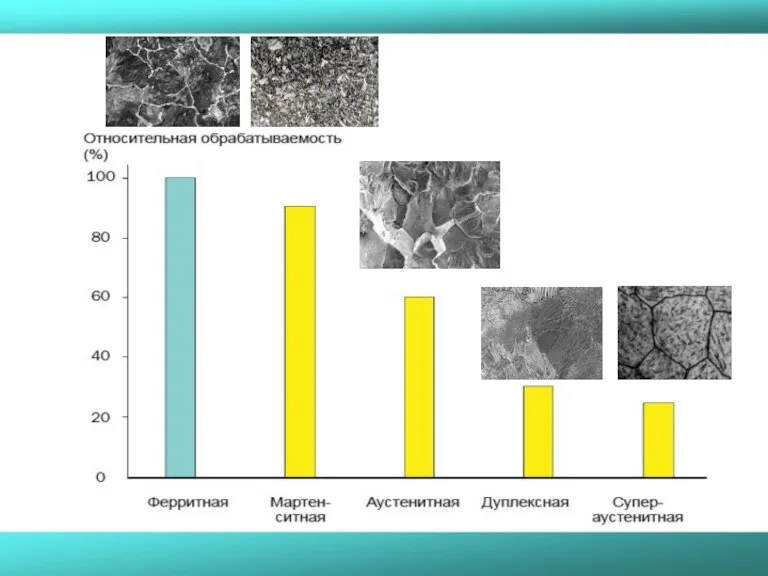
Формирование стружки для различных групп материалов

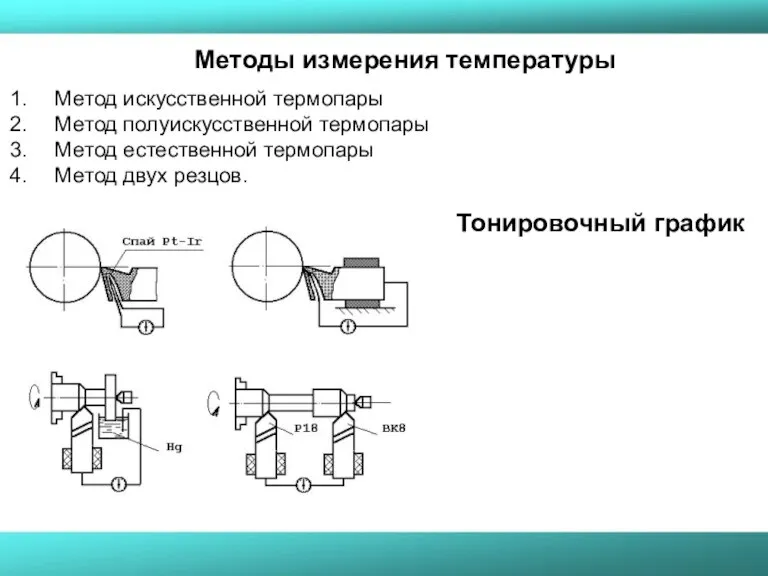
Методы измерения температуры
Метод искусственной термопары
Метод полуискусственной термопары
Метод естественной термопары
Метод двух резцов.
Тонировочный график

где Q – теплота при резании, С;
СQ – константа для условий резания;
t – глубина резания, мм;
S – подача, мм/об;
V – скорость резания, м/мин;
XQ, YQ, ZQ – показатели степени.
XQ = 0,1…0,2
YQ = 0,2…0,25
ZQ = 0,4…0,6
Экспериментальные методы определения температуры

На обрабатываемость материала влияет три основных фактора.
1. Классификация обрабатываемого материала с точки зрения металлургии/механики.
2. Микро- и макро геометрия режущей кромки.
3. Материал режущего инструмента (марка сплава), например, твёрдый сплав с покрытием, керамика, CBN, PCD и пр.
Обрабатываемость

Определение
• Сталь - самая крупная по составу группа
обрабатываемых материалов.
• Сталь может быть незакалённой, закалённой или
отпущенной и иметь твёрдость до 400 HB. Стали
твёрдостью в пределах от 48 до 65 HRC относятся к
группе ISO H.
• Сталь - это сплав, основным компонентом которого
является железо (Fe).
• Нелегированные стали содержат менее 0,8% углерода, остальную часть составляет железо без добавления легирующих элементов.
• Легированные стали содержат до 1,7% углерода, а также в их состав входят такие элементы как Ni, Cr, Mo, V и W.
• В низколегированных сталях содержание легирующих элементов составляет менее 5%.
• В высоколегированных сталях содержание легирующих элементов превышает 5%.
• Удельная сила резания kc1 = 1400-3100 Н/мм.
• Сила резания и, соответственно, необходимая для обработки мощность находятся в пределах ограниченного диапазона.
Сталь
Лекция 7

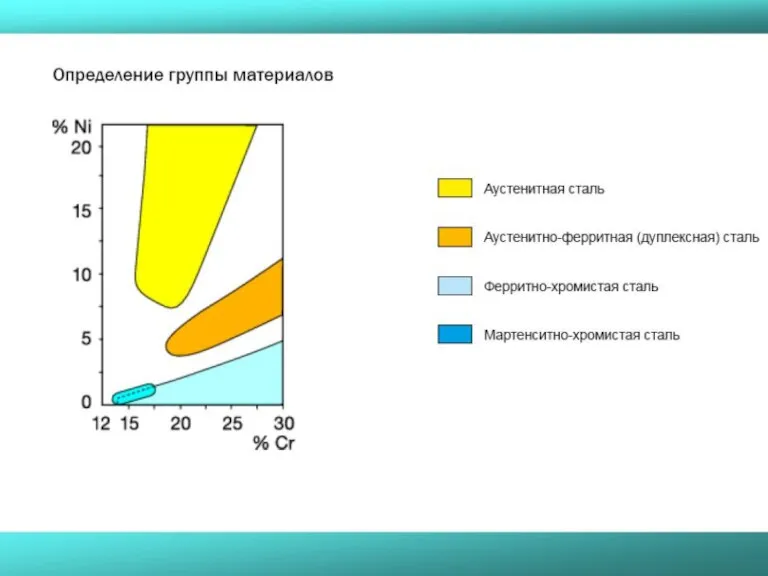
Нержавеющая сталь
Определение
• Сплав на основе железа как основного компонента (Fe).
• Содержание хрома превышает 12%.
• Как правило, с низким содержанием углерода
(C ≤ 0,05 %).
• Добавление элементов, таких как никель (Ni), хром (Cr), молибден (Mo), ниобий (Nb) и титан (Ti) определяет разные эксплуатационные свойства сплава, например, стойкость к коррозии или прочность при высоких температурах.
• Хром при взаимодействии с кислородом (O) образует пассивирующий слой Cr2O3 на поверхности стали, что придает ей стойкость к коррозии.
• Материал, дающий сливную стружку.
• Удельная сила резания: 1800-2850 Н/мм².
• Механическая обработка нержавеющих сталей характеризуется значительными усилиями резания,
наростообразованием на кромке, а также наблюдается упрочнение поверхностного слоя.
• Сера (S) повышает обрабатываемость нержавеющей стали.

Чугун
Определение
Существует 5 основных типов чугуна:
• Серый чугун (GCI),
• Ковкий чугун (MCI),
• Чугун с шаровидным графитом (NCI),
• Чугун с вермикулярным графитом (CGI)
• Отпущенный ковкий чугун (ADI).
Чугун - это сплав железа с углеродом и относительновысоким содержанием кремния (1-3%). Содержание углерода в чугуне превышает 2%, что является
максимальной растворимостью углерода в аустенитной фазе. Хром (Cr), молибден (Mo) и ванадий (V) образуют карбиды, придающие прочность и твёрдость, но ухудшающие обрабатываемость чугуна.
• При обработке чугуна не возникает трудностей со стружкодроблением, так как образуется короткая
сыпучая стружка. Удельная сила резания: 790 – 1350 Н/мм².
• При обработке на высокой скорости, особенно чугунов с включениями песка, происходит абразивный износ инструмента.
• Чугуны NCI, CGI и ADI требуют особого внимания из-за разных механических свойств и наличия графита в матрице в отличие от обычного чугуна GCI.
• Чугуны часто обрабатывают пластинами без задних углов, имеющими прочные кромки и надёжными в применении.

Цветные металлы
Определение:
• В эту группу входят цветные, мягкие металлы твёрдостью до 130 HB, кроме высокопрочной бронзы (>225HB).
• Сплавы алюминия (Al) с содержанием кремния (Si) до 12-13% - самая крупная подгруппа.
• MMC: композитный материал с металлической матрицей, Al + SiC (20-30%).
• Сплавы на основе магния
• Медь, электролитическая медь (99,95% Cu).
• Бронза: сплав меди с оловом (Sn) (10-14%) и/или
алюминием (3-10%).
• Латунь: сплав меди (60-85%) с цинком (Zn) (15-40%).
Обрабатываемость алюминия
• Материал, дающий длинную стружку.
• Относительно хорошее стружкодробление при условии легирования.
• Чистый алюминий вязок и требует острых режущих кромок и высокой скорости резания vc.
• Удельная сила резания: 350–700 Н/мм².
• Усилия резания и, соответственно, мощность, необходимая для резания, небольшие.
• При содержании кремния до 7-8% можно обрабатывать мелкозернистыми твёрдыми сплавами без покрытия, а при большем содержании кремния - сплавами с вставками из PCD для алюминия.
• Алюминий с содержанием кремния >12% очень абразивен.

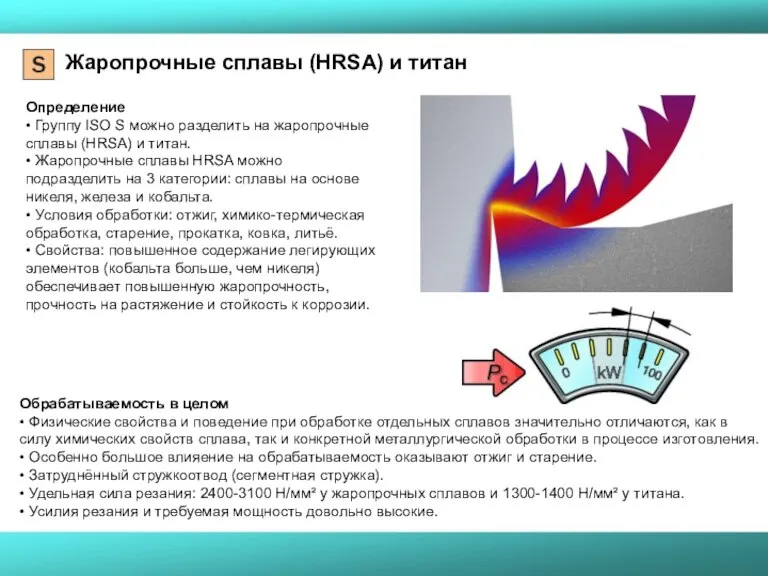
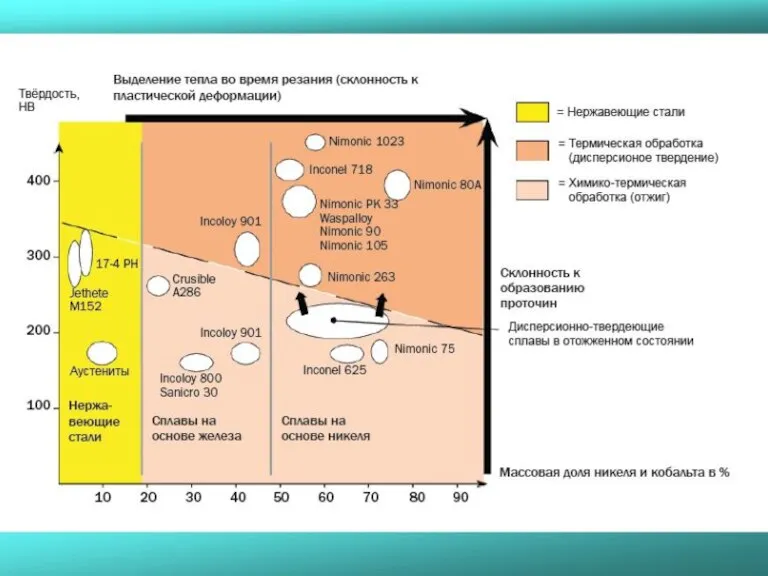
Жаропрочные сплавы (HRSA) и титан
Определение
• Группу ISO S можно разделить на жаропрочные сплавы (HRSA) и титан.
• Жаропрочные сплавы HRSA можно подразделить на 3 категории: сплавы на основе никеля, железа и кобальта.
• Условия обработки: отжиг, химико-термическая
обработка, старение, прокатка, ковка, литьё.
• Свойства: повышенное содержание легирующих
элементов (кобальта больше, чем никеля) обеспечивает повышенную жаропрочность, прочность на растяжение и стойкость к коррозии.
Обрабатываемость в целом
• Физические свойства и поведение при обработке отдельных сплавов значительно отличаются, как в
силу химических свойств сплава, так и конкретной металлургической обработки в процессе изготовления.
• Особенно большое влияение на обрабатываемость оказывают отжиг и старение.
• Затруднённый стружкоотвод (сегментная стружка).
• Удельная сила резания: 2400-3100 Н/мм² у жаропрочных сплавов и 1300-1400 Н/мм² у титана.
• Усилия резания и требуемая мощность довольно высокие.

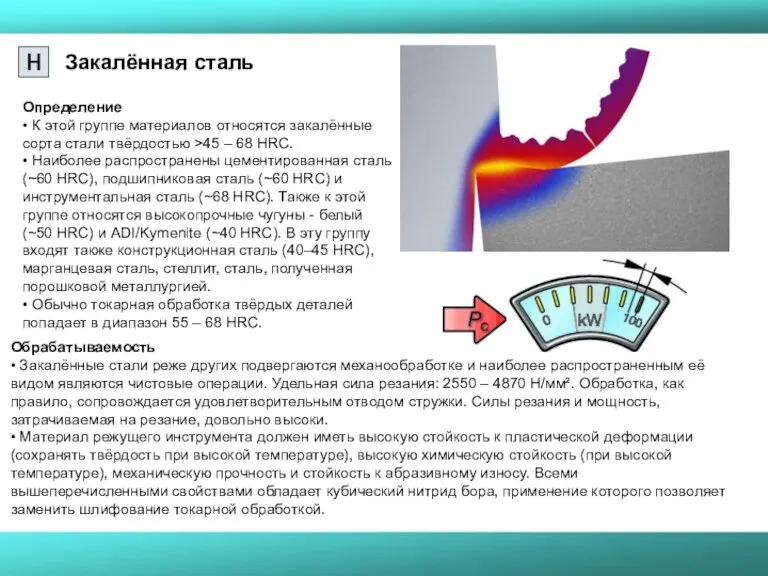
Закалённая сталь
Определение
• К этой группе материалов относятся закалённые сорта стали твёрдостью >45 – 68 HRC.
• Наиболее распространены цементированная сталь (~60 HRС), подшипниковая сталь (~60 HRС) и
инструментальная сталь (~68 HRС). Также к этой группе относятся высокопрочные чугуны - белый (~50 HRC) и ADI/Kymenite (~40 HRC). В эту группу входят также конструкционная сталь (40–45 HRС), марганцевая сталь, стеллит, сталь, полученная порошковой металлургией.
• Обычно токарная обработка твёрдых деталей попадает в диапазон 55 – 68 HRC.
Обрабатываемость
• Закалённые стали реже других подвергаются механообработке и наиболее распространенным её
видом являются чистовые операции. Удельная сила резания: 2550 – 4870 Н/мм². Обработка, как правило, сопровождается удовлетворительным отводом стружки. Силы резания и мощность, затрачиваемая на резание, довольно высоки.
• Материал режущего инструмента должен иметь высокую стойкость к пластической деформации (сохранять твёрдость при высокой температуре), высокую химическую стойкость (при высокой температуре), механическую прочность и стойкость к абразивному износу. Всеми вышеперечисленными свойствами обладает кубический нитрид бора, применение которого позволяет заменить шлифование токарной обработкой.

Основные положения теории подобия
Физические явления, процессы или системы подобны, если в сходственные моменты времени в сходственных точках пространства значения переменных величин, характеризующих состояние одной системы, пропорциональны соответствующим величинам другой системы.
Коэффициенты пропорциональности для каждой из величин называется коэффициентом подобия.
Основные числа теплового подобия.
Число Нуссельта является мерой соотношения между интенсивностью теплоотдачи и интенсивностью теплопроводности в пограничном слое (λ0 – коэффициент теплопроводности в потоке жидкости или газа).
Лекция 8

Число Био является мерой соотношения между внутренним термическим сопротивлением тела и термическим сопротивлением теплоотдачи на его поверхности (λS – коэффициент теплопроводности твердого тела, т.е. стенки, с которой контактирует поток жидкости или газа).
Число Пекле является мерой отношения конвективного и молекулярного переноса теплоты в потоке (v – скорость перемещения потока).
Используется при построении расчётных схем (метод конечных разностей, метод конечных элементов) для решения дифференциальных уравнений в частных производных, описывающих течения вязкой жидкости.

Число Прандтля — один из критериев подобия тепловых процессов в жидкостях и газах, учитывает влияние физических свойств теплоносителя на теплоотдачу:
Число Фурье характеризует связь между скоростью изменения температурного поля, физическими свойствами и размерами тела.
Основные числа гидродинамического подобия.
Число Рейнольдса характеризует гидродинамический режим движения, являясь мерой отношения сил инерции и сил вязкого трения в потоке (ν - коэффициент кинематической вязкости потока жидкости или газа).
;
— кинематическая вязкость;
— характерное время изменения внешних условий
— характерная скорость
— кинематическая вязкость среды

Число Грасгофа является мерой отношения подъемной силы, возникающей вследствие разности плотностей жидкости, к силе вязкого трения (g – ускорение свободного падения, β – коэффициент термического расширения жидкости, Δt – разность температур в различных частях системы, ℓ - определяющий линейный размер)
— кинематическая вязкость среды

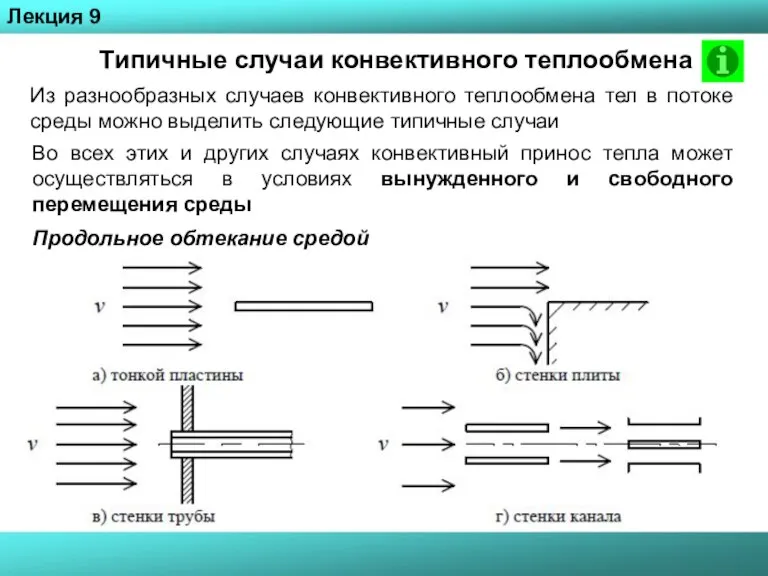
Типичные случаи конвективного теплообмена
Из разнообразных случаев конвективного теплообмена тел в потоке среды можно выделить следующие типичные случаи
Продольное обтекание средой
Во всех этих и других случаях конвективный принос тепла может осуществляться в условиях вынужденного и свободного перемещения среды
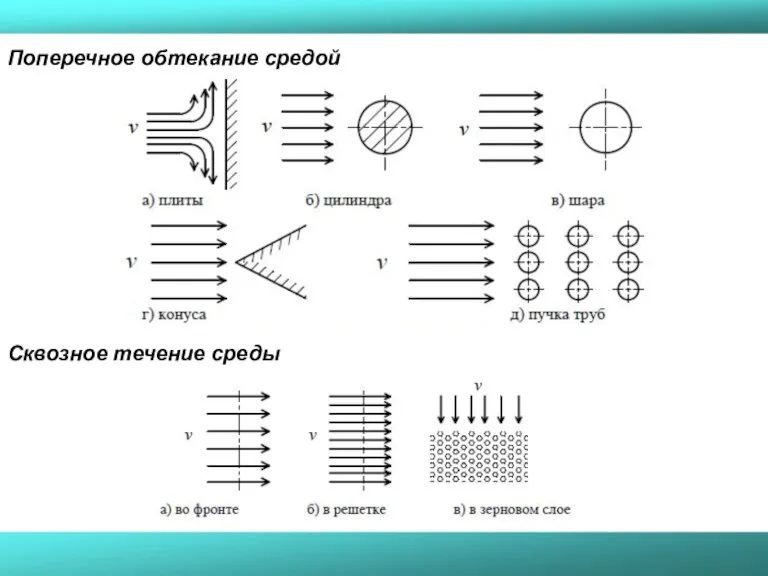
Лекция 9

Сквозное течение среды
Поперечное обтекание средой

Теплоотдача при естественной конвекции
Рассмотрим определение α при естественной конвекции. При обтекании тел средой, движение которой вызвано только различием температур среды у поверхности тела и в отдалении от нее перемещение масс среды, происходит под действием подъемной силы, возникающей в поле тяготения при изменении плотности нагреваемой и охлаждающей среды (т. е. возникает Архимедова сила).
Причем С1 относится к теплоотдаче вертикальных и горизонтальных валов (характерный линейный размер соответственно длина и диаметр вала), шаров и вертикальных плит (характерный размер – высота плиты);
С2 – горизонтальные плиты при теплоотдаче, направленной вверх;
С3 – при теплоотдаче, направленной вниз.
Значения коэффициента Сi и показателя степени n в зависимости от произведения Gr ⋅ Pr приведены в таблице

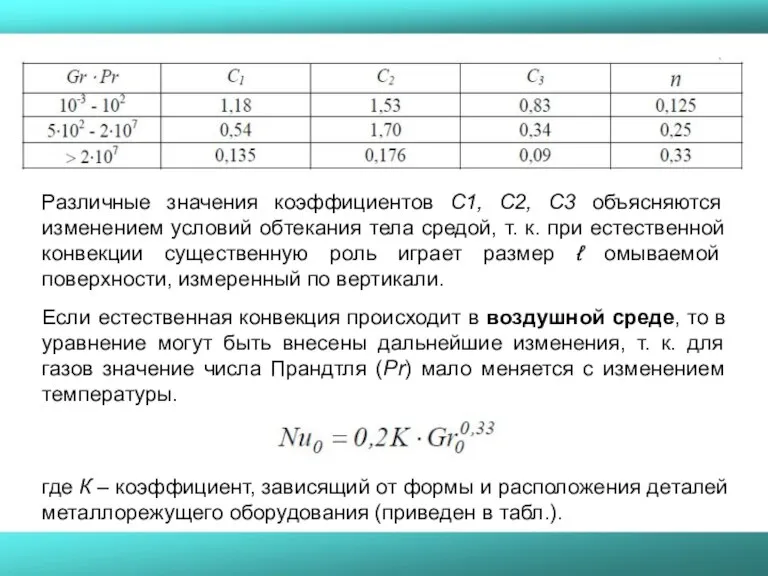
Различные значения коэффициентов С1, С2, С3 объясняются изменением условий обтекания тела средой, т. к. при естественной конвекции существенную роль играет размер ℓ омываемой поверхности, измеренный по вертикали.
Если естественная конвекция происходит в воздушной среде, то в уравнение могут быть внесены дальнейшие изменения, т. к. для газов значение числа Прандтля (Рr) мало меняется с изменением температуры.
где К – коэффициент, зависящий от формы и расположения деталей металлорежущего оборудования (приведен в табл.).

Теплоотдача при вынужденной конвекции
В технологических системах твердые тела могут обмениваться теплотой с жидкостью или газом, движущимися принудительно. Теплообмен такого вида возникает на поверхностях заготовки и инструмента, под воздействием смазочно-охлаждающих технологических сред (водных растворов, эмульсий, масел или струй сжатого воздуха). Такой вид теплоотдачи происходит в узлах оборудования, принудительно смазываемых и охлаждаемых маслами или сжатым воздухом (например, в аэродинамических подшипниках).
учитывает направление потока теплоты в жидкости.

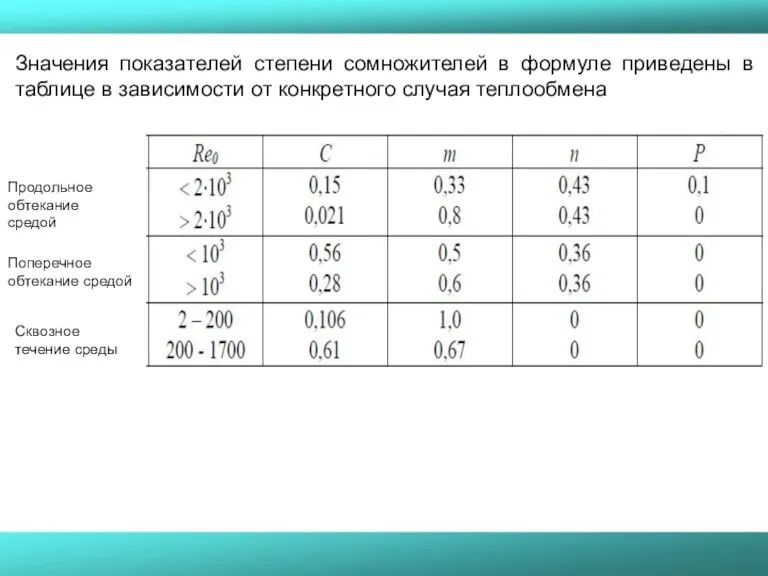
Продольное обтекание средой
Поперечное обтекание средой
Сквозное течение среды
Значения показателей степени сомножителей в формуле приведены в таблице в зависимости от конкретного случая теплообмена

Обобщенный алгоритм теплофизического анализа
В зависимости от целей анализа, могут быть поставлены задачи определить:
• законы распределения температур на различных участках ТС;
• средние температуры на поверхности тел;
• максимальные температуры, которые возникают в ТС на наиболее нагруженных или ответственных участках.
Лекция 10

Обобщенный алгоритм ТФА.
1. Выяснить число и местоположение источников и стоков теплоты в системе или подсистеме. Установить время функционирования и мощность каждого из источников.
2. Определить размеры и конфигурацию площадок или объемов, внутри которых действуют источники или стоки теплоты. Установить (или принять) законы распределения плотности потоков для каждого источника истока.
3. Схематизировать форму и свойства твердых тел, а также форму и другие характерные особенности источников и стоков теплоты.
4. Принять вид математического описания граничных условий на поверхностях твердых тел, не занятых источниками и стоками теплоты.
5. Разработать структурную схему теплообмена.
6. Составить коды тепловых задач для каждого их твердых тел, входящих в структурную схему теплообмена.

7. В соответствии с кодом тепловой задачи установить вид теоретических расчетных формул и поправок к ним, полученным экспериментальным путем. По этим формулам составить расчетные выражения для определения средней температуры на каждой из контактных площадок каждого из твердых тел.
8. Решить совместно выражения для определения средних температур на контактных площадках соприкасающихся тел и таким путем рассчитать плотности итоговых потоков теплообмена между твердыми телами, входящими в ТС.
9. Окончательно сформулировать математические закономерности, отвечающие целям ТФА (распределение температур, средняя или наибольшая температура).
10. Разработать предложения по оптимизации процессов и конструкций в ТС, вытекающих из ТФА.