Содержание
- 2. Целью освоения дисциплины является достижение следующих компетенций на уровнях: профессионально-специализированных: - способен выполнять расчёты простых систем,
- 4. Литература В. В. Нащокин. Техническая термодинамика и теплопередача. М.: Высшая школа, 1980, 74 экз. В. В.
- 6. Понятия и определения
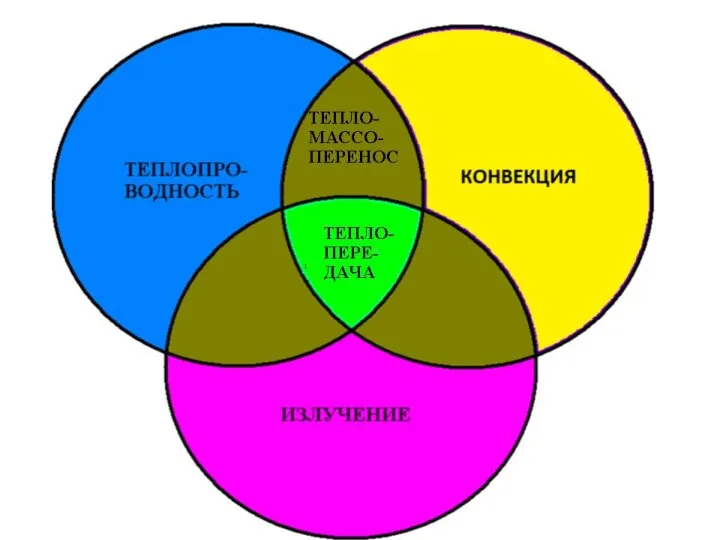
- 8. Теплообмен (теплопередача) Это самопроизвольный, необратимый процесс распространения теплоты в пространстве, обусловленный разностью температур. Различают три элементарных
- 9. Теплопроводность Это процесс переноса тепла, осуществляемый в результате непосредственного контакта микрочастиц, обладающих различной энергией.
- 10. Конвекция Это процесс переноса теплоты вследствие пространственного перемещения макрообъемов вещества с различной температурой. Причем, внутри макрообъемов
- 11. Тепловое излучение Это процесс переноса теплоты посредством электромагнитного поля с двойным взаимным превращением – теплоты в
- 12. Сложный теплообмен Это теплообмен, осуществляемый в результате одновременного действия теплопроводности, конвекции и излучения.
- 13. Температурное поле Это совокупность мгновенных значений температуры во всех точках пространства. Поле температур является скалярным полем,
- 14. стационарный тепловой режим Режим теплообмена, при котором во всех точках пространства температура не изменяется во времени.
- 15. Стационарное, двухмерное поле. Т= Т(х, у) Одномерное стационарное поле. Т = ƒ(х) Одномерное нестационарное поле Т
- 16. Изотермическая поверхность Это геометрическое место точек пространства, имеющих одинаковую температуру
- 17. Температурный градиент Это физическая величина, которая описывает, в каком направлении и с какой скоростью температура меняется
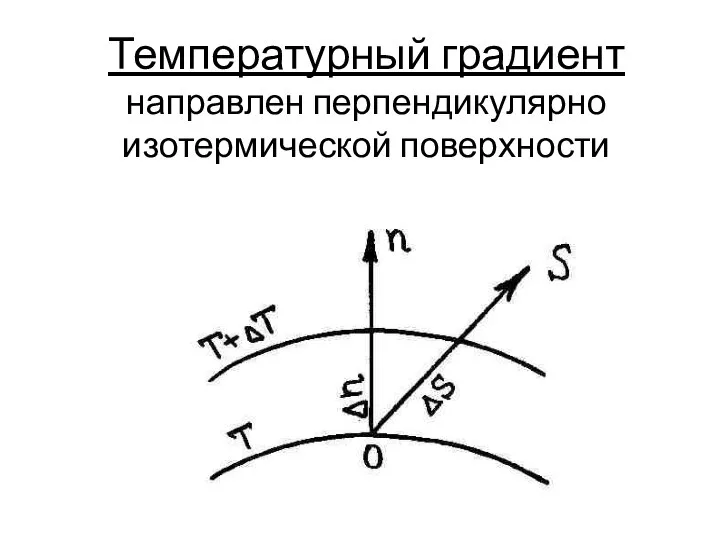
- 18. Температурный градиент направлен перпендикулярно изотермической поверхности
- 19. Температурный градиент Это предел отношения разности температур на изотермических поверхностях ΔТ к расстоянию между ними по
- 20. Температурный градиент Это вектор, определенный в каждой точке температурного поля, направленный по нормали к изотермической поверхности
- 21. Температурный градиент является мерой интенсивности изменения температуры. Таким образом, скалярному полю температур соответствует векторное поле температурных
- 22. Тепловой поток Это количество теплоты, участвующее в теплообмене: Q, вт. Плотность теплового потока Это количество теплоты,
- 23. Плотность теплового потока q и тепловой поток Q являются векторами, направленными в сторону уменьшения температуры.
- 24. Основной задачей расчета процессов теплообмена является в конечном итоге, выявление количественной зависимости между распределением температуры и
- 25. Раздел 1 СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
- 26. Закон Фурье (1822 г.) дает связь поля температурных градиентов и поля тепловых потоков. Он устанавливает, что
- 27. Закон Фурье
- 28. Коэффициент теплопроводности λ Вт/(м0К). Коэффициент λ это физический параметр, характеризующий способность вещества проводить теплоту. Он численно
- 29. Зависимость λ =λ(Т) Для большинства веществ зависимость λ =λ(Т) имеет линейный характер. У газов, а также
- 30. Численные значения коэффициента теплопроводности Для газов λ = 0,05 ÷ 0,5Вт/(м0К); Для капельных жидкостей λ =0,07÷0,7
- 35. Дифференциальное уравнение теплопроводности
- 36. Допущения: 1) среда – однородная и изотропная; 2) внутренние источники тепла отсутствуют; 3) конвекция отсутствует (среда
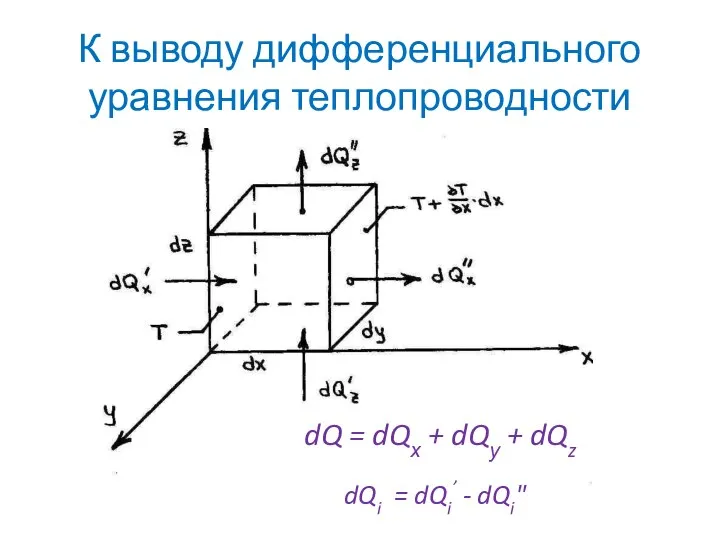
- 37. К выводу дифференциального уравнения теплопроводности dQ = dQх + dQу + dQz dQi = dQi’ -
- 38. Внутренняя энергия выделенного объема может изменяться только за счет теплообмена с окружающей средой dU = dQ,
- 39. Величина dQ является суммой трех слагаемых, которые выражают тепловые потоки, поступающие в элемент (или из него)
- 40. Каждое из слагаемых можно представить как разность между потоками, входящими в элемент и выходящими из него
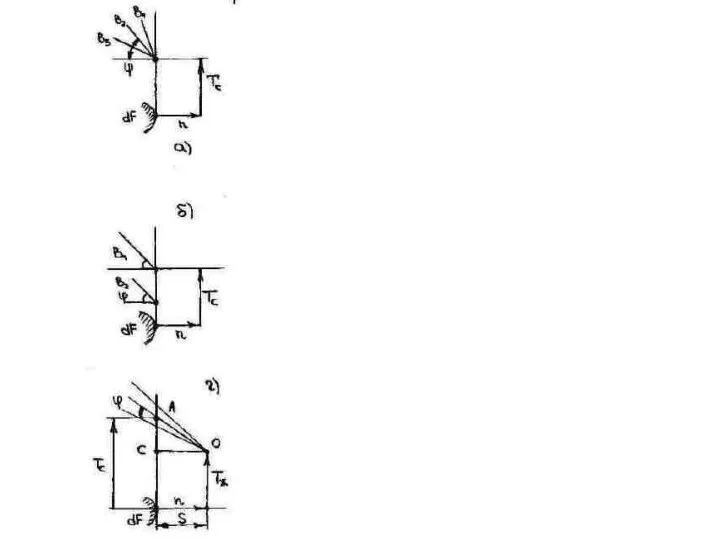
- 41. dQ = q dF dτ, Температуры на гранях имеют значение на левой (вход): Т на правой
- 42. Исходя из закона Фурье получаем:
- 44. Аналогично получаем dQ по осям Y и Z. Далее, суммируя их, получаем общее количество теплоты, затраченное
- 47. Дифференциальное уравнение теплопроводности
- 48. Коэффициент температуропроводности
- 49. коэффициент температуропроводности м2/с Характеризует теплоинерционные свойства вещества, т.е. его способность с той или иной скоростью изменять
- 50. Дифференциальное уравнение Фурье относится к числу общих уравнений. Чтобы получить из бесконечного множества решений единственное, отвечающее
- 51. Условия однозначности
- 52. Условия однозначности (единственности) решения состоят из величин, учитывающих индивидуальные различия процессов, т.к. развитие процесса зависит от:
- 53. Условия однозначности геометрические, характеризующие форму и размеры системы, в которой протекает процесс; физические, учитывающие физические параметры
- 55. Способы задания однозначности I рода: Т= Т( х, у, z,τ); II рода: q = q( х,
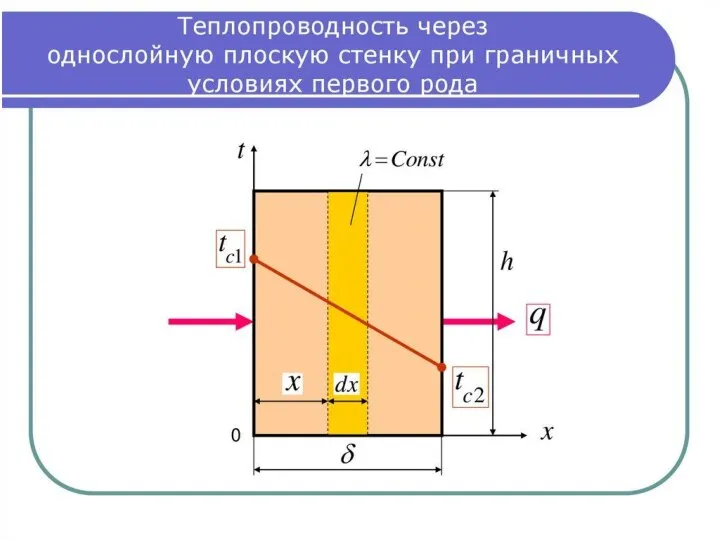
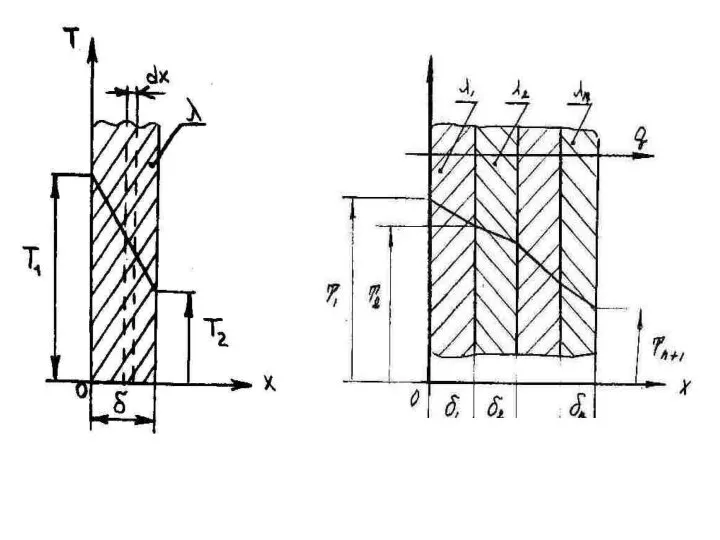
- 56. Теплопроводность плоской стенки
- 59. Дифференциальное уравнение теплопроводности (выведено ранее)
- 60. Теплопроводность плоской однослойной стенки Температурное поле стационарное, одномерное: Первое интегрирование: Второе интегрирование:
- 62. Теплопроводность многослойной плоской стенки
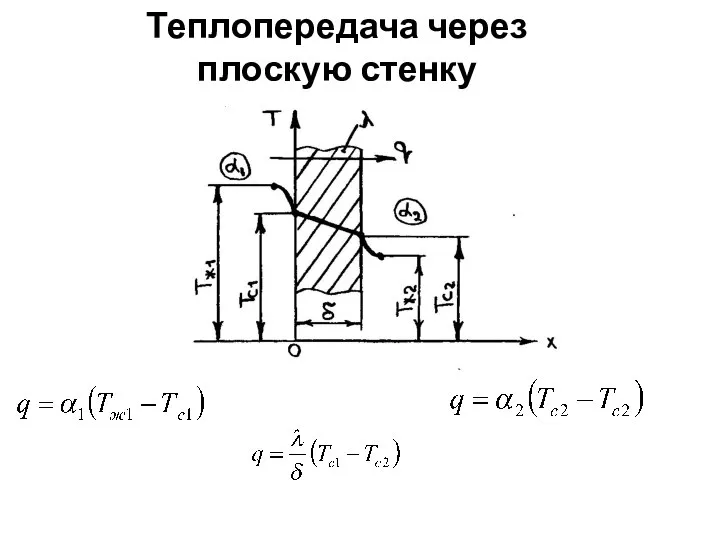
- 63. Теплопередача через плоскую стенку
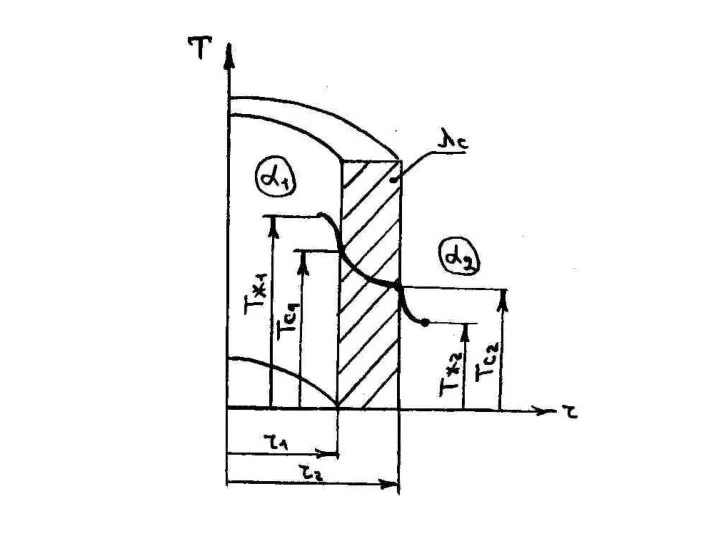
- 64. частные температурные напоры
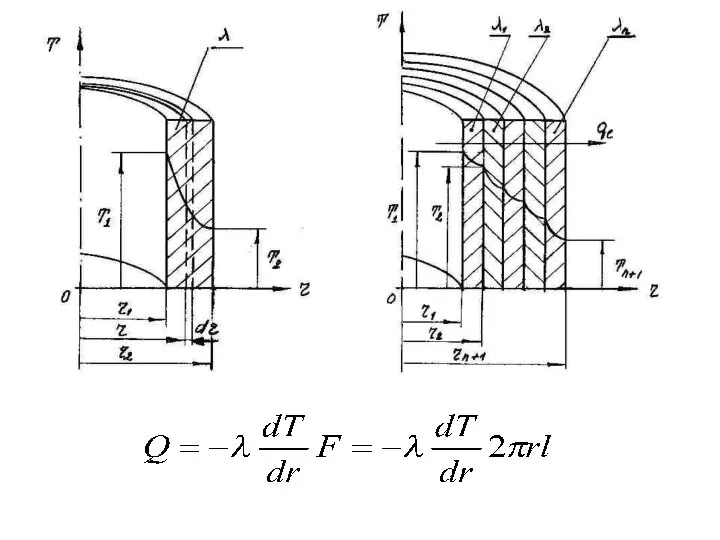
- 66. Теплопроводность цилиндрической стенки
- 68. Для однослойной цилиндрической стенки:
- 69. Для многослойной цилиндрической стенки
- 70. Теплопередача через цилиндрическую стенку
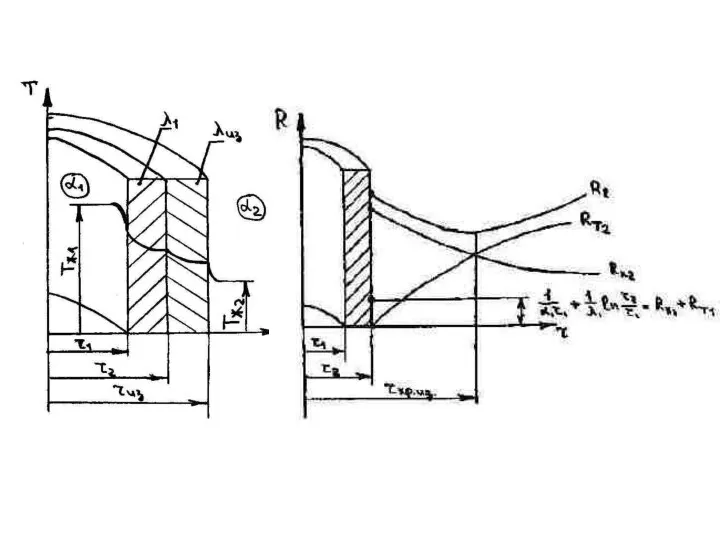
- 76. Тепловая изоляция. Критический радиус изоляции.
- 78. λиз ≤ α2 r2 rкр из ≤ α2 r2
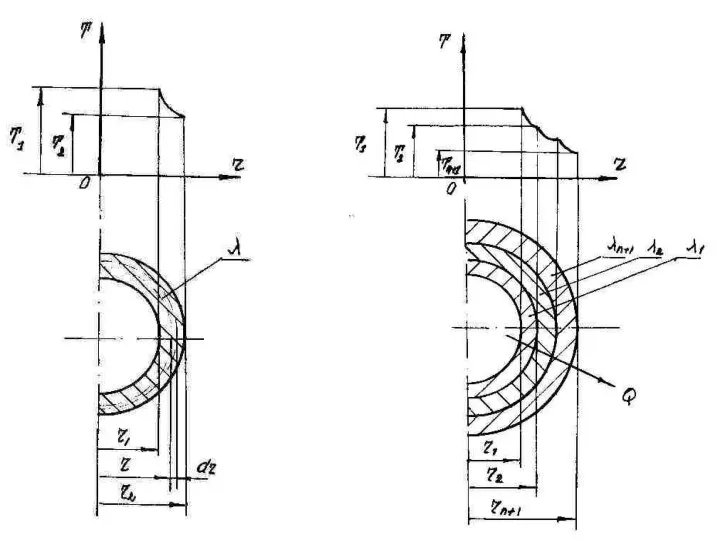
- 79. Теплопроводность сферической стенки
- 81. Для однослойной стенки
- 83. Для многослойной стенки
- 84. Теплопередача через сферическую стенку
- 87. Радиус критической изоляции шара
- 88. Нестационарная теплопроводность
- 89. Понятие «нестационарная теплопроводность»
- 90. При нестационарном тепловом режиме температурное поле изменяется во времени. Нестационарность тепловых процессов обуславливается изменением внутренней энергии
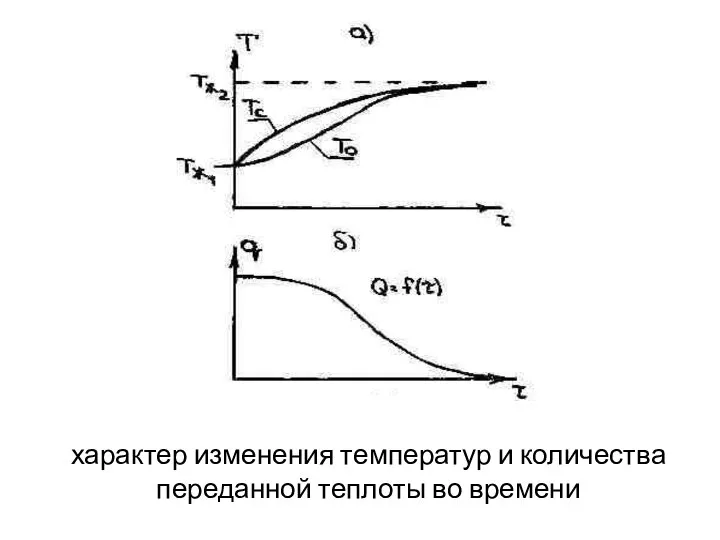
- 91. характер изменения температур и количества переданной теплоты во времени
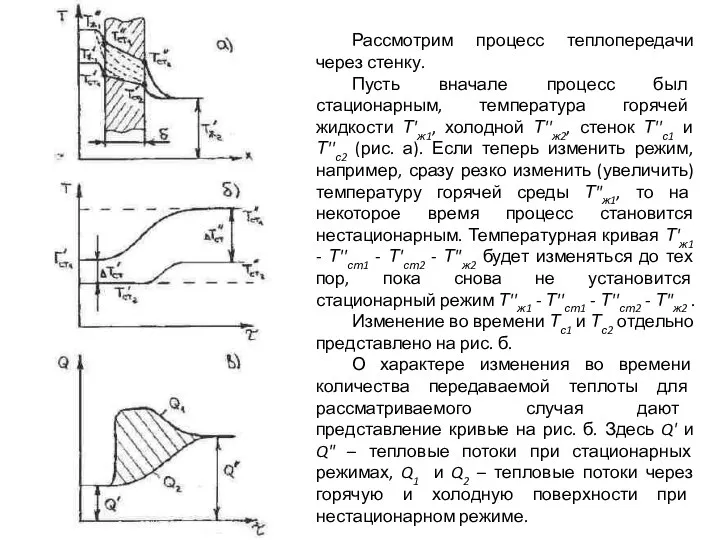
- 92. Рассмотрим процесс теплопередачи через стенку. Пусть вначале процесс был стационарным, температура горячей жидкости Т'ж1, холодной Т''ж2,
- 93. Нестационарный тепловой процесс всегда связан с изменением внутренней энергии тела и им обуславливается. Так как скорость
- 94. В задачах нестационарной теплопроводности выделяют три характерных режима. I режим. Начальный. Охватывает начало процесса, когда существенно
- 95. Решить задачу нестационарной теплопроводности – значит найти зависимость изменения температуры и количества тепла для любой точки
- 96. Расчет нагрева и остывания термически тонких тел
- 97. Наиболее простым но достаточно часто распространенным является случай, когда удельное тепловое сопротивление теплоотдачи 1/α от греющей
- 98. В каждый момент времени температура Т внутри такого тела успевает выровняться за счет интенсивного переноса теплоты
- 99. Согласно начальным условиям: при τ = 0
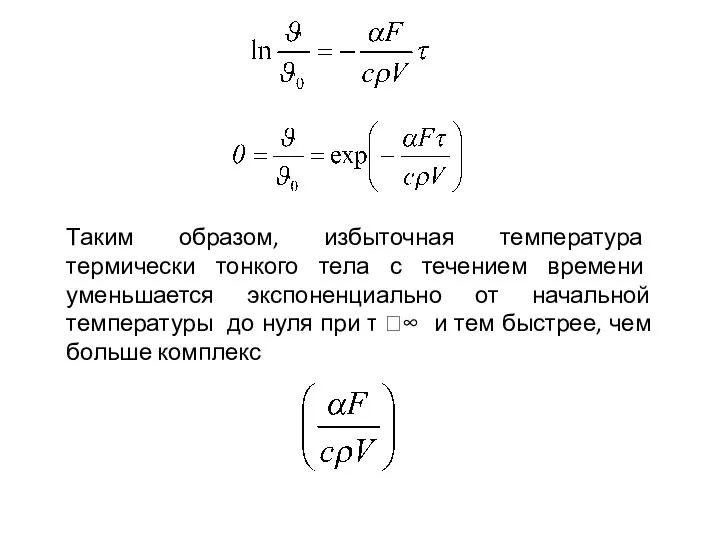
- 100. Таким образом, избыточная температура термически тонкого тела с течением времени уменьшается экспоненциально от начальной температуры до
- 101. Регулярный тепловой режим
- 102. m [1/сек] – темп охлаждения (нагревания). Характеризует интенсивность охлаждения (нагревания) тела. * **
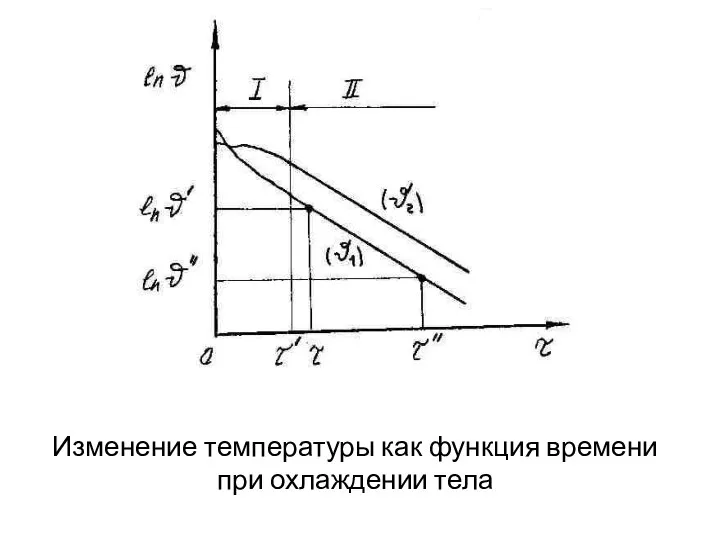
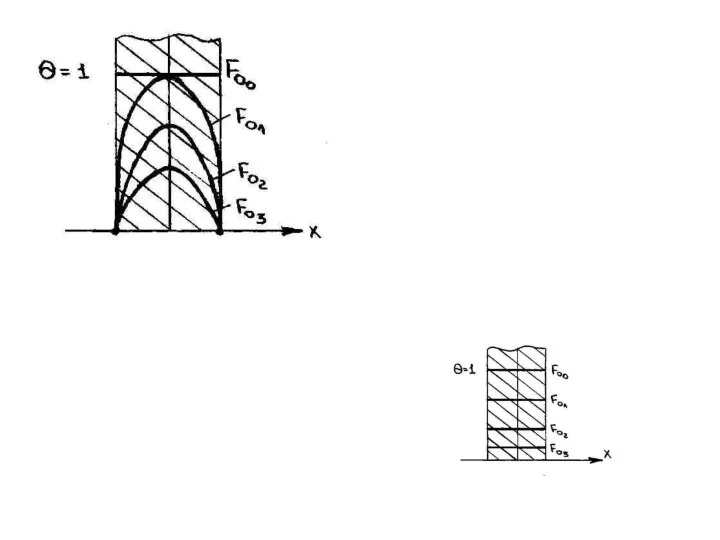
- 103. Изменение температуры как функция времени при охлаждении тела
- 104. Применим уравнение (**) к двум произвольным моментам времени τ’ и τ” и, исключив постоянную С, получим
- 111. Скачать презентацию






































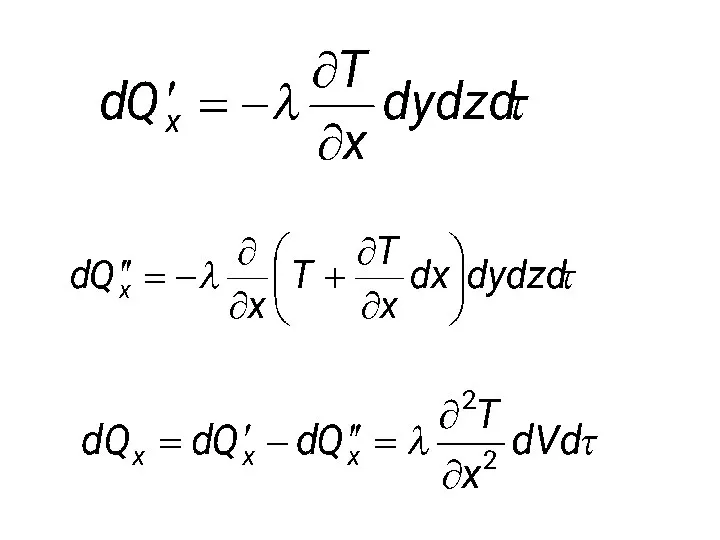

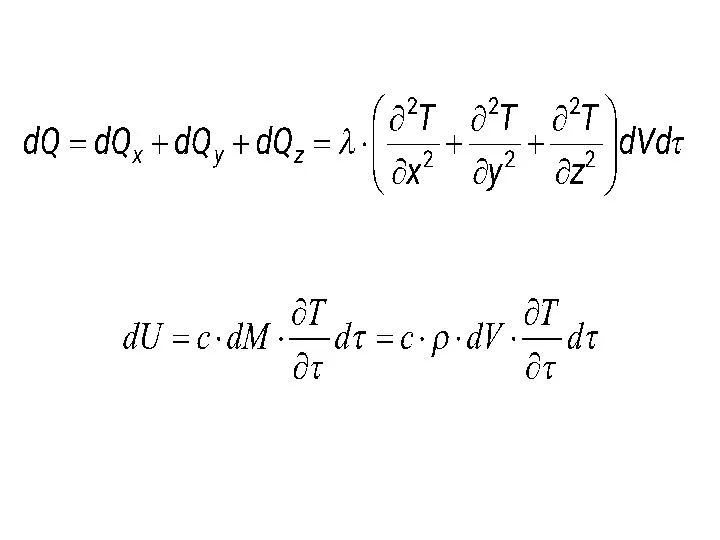
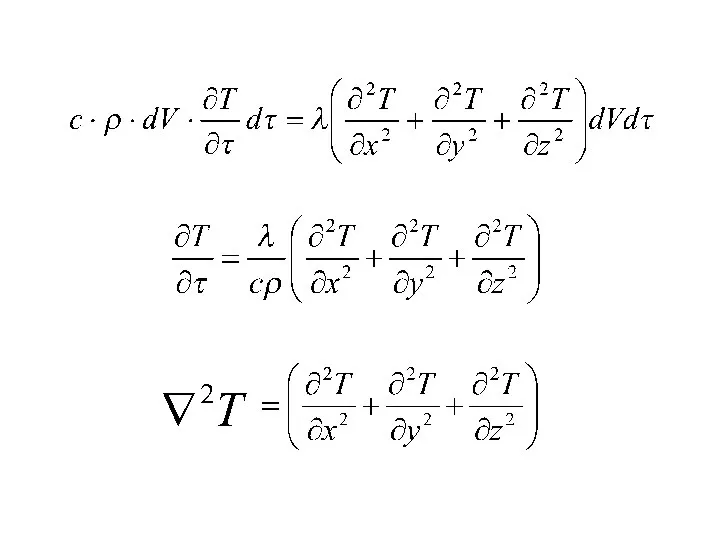

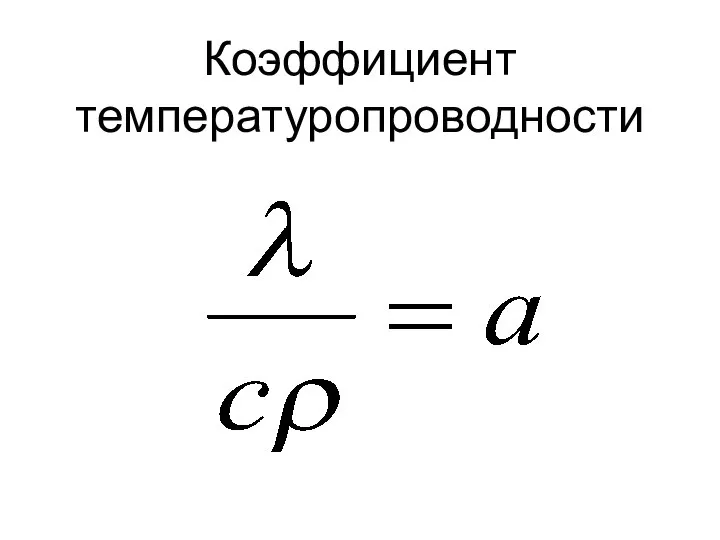










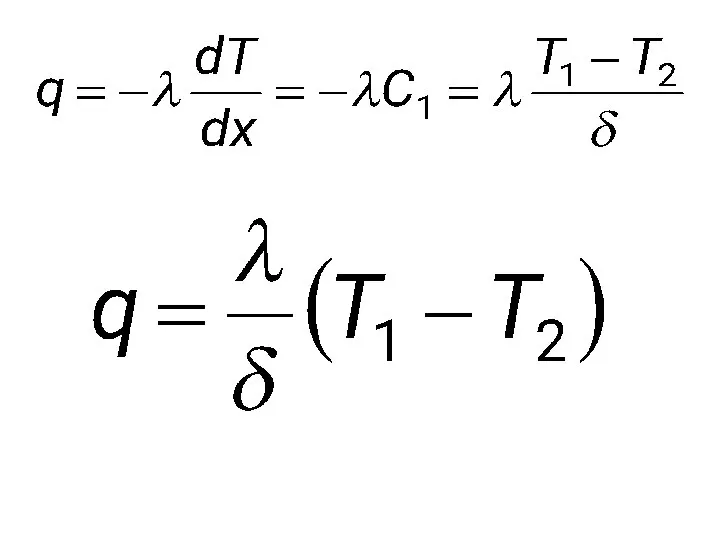


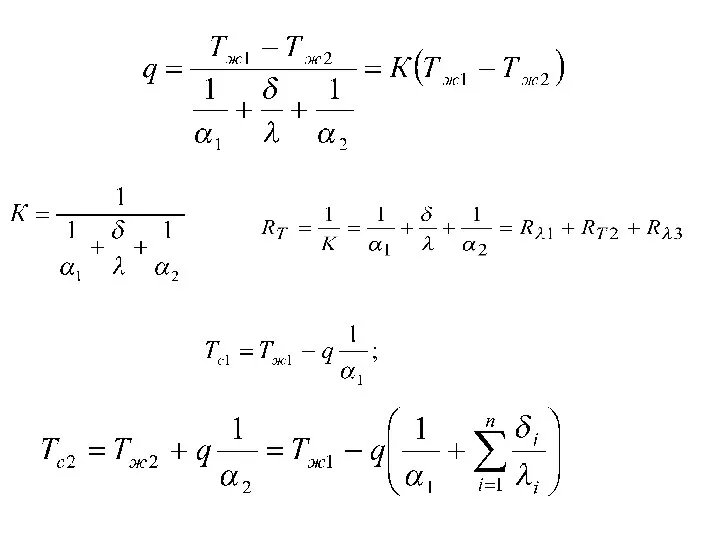




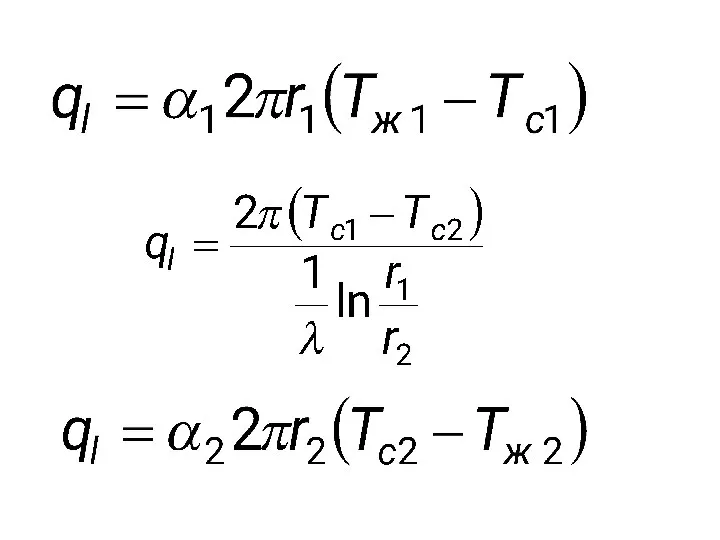
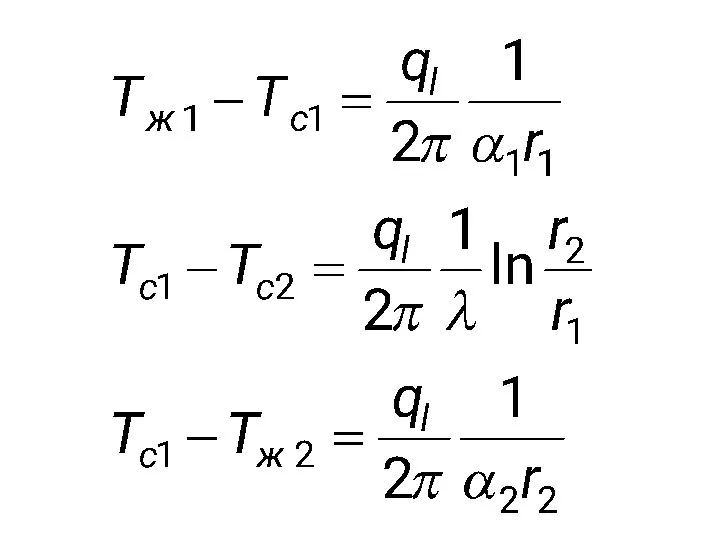
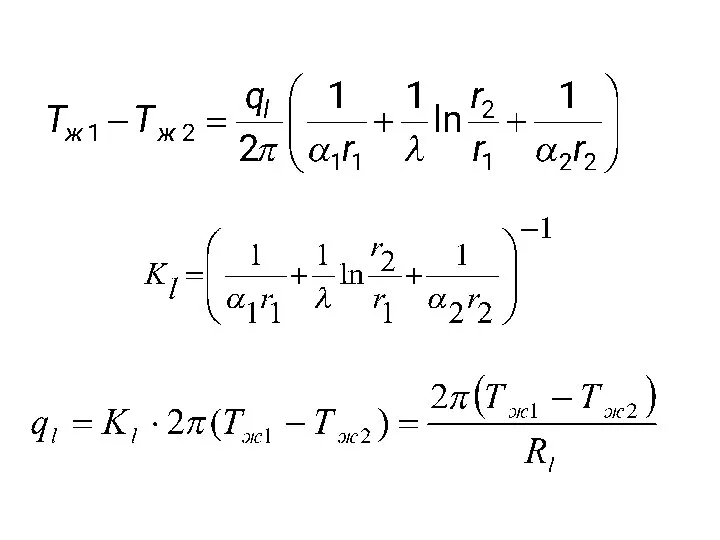
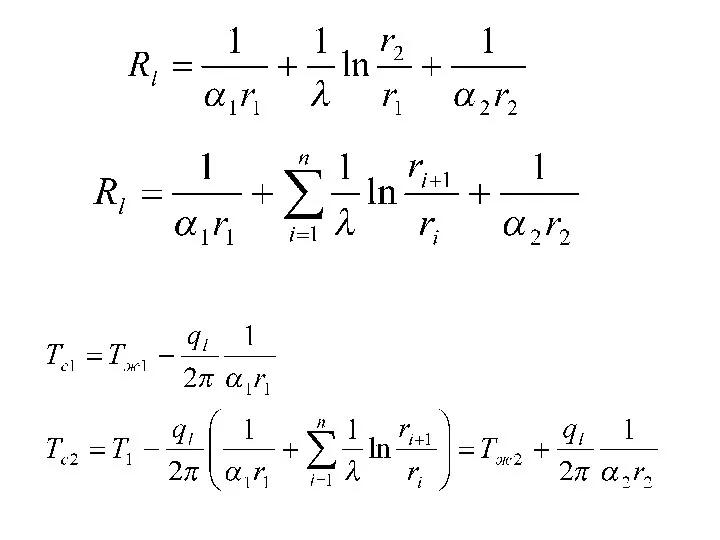

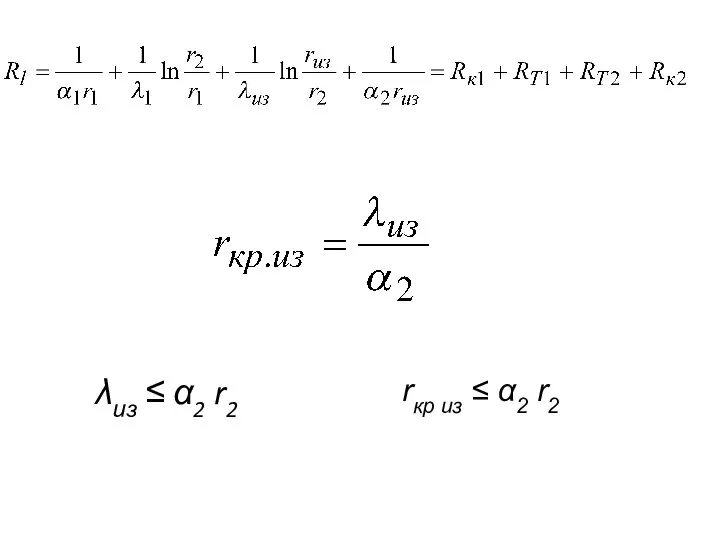


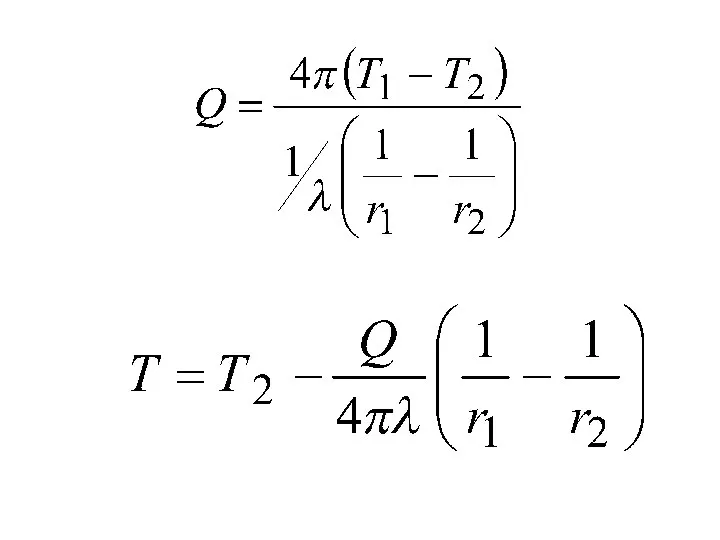


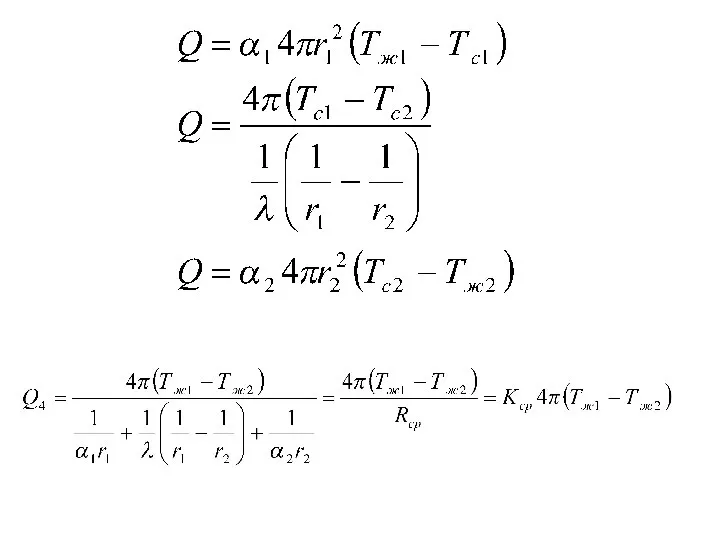
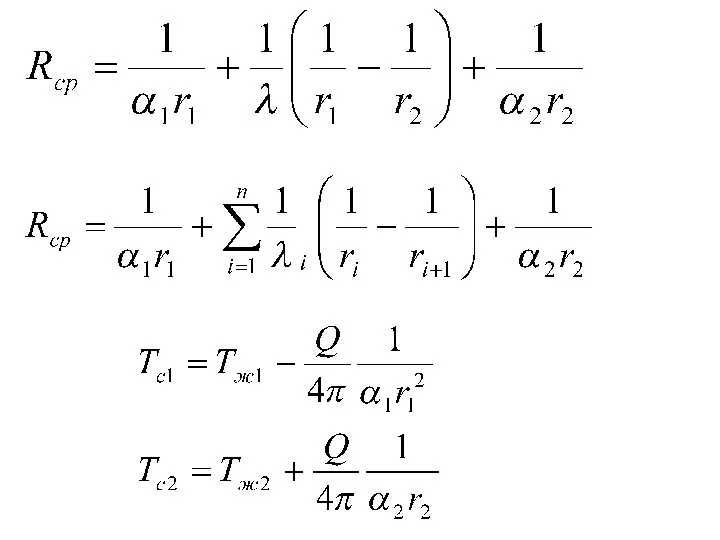










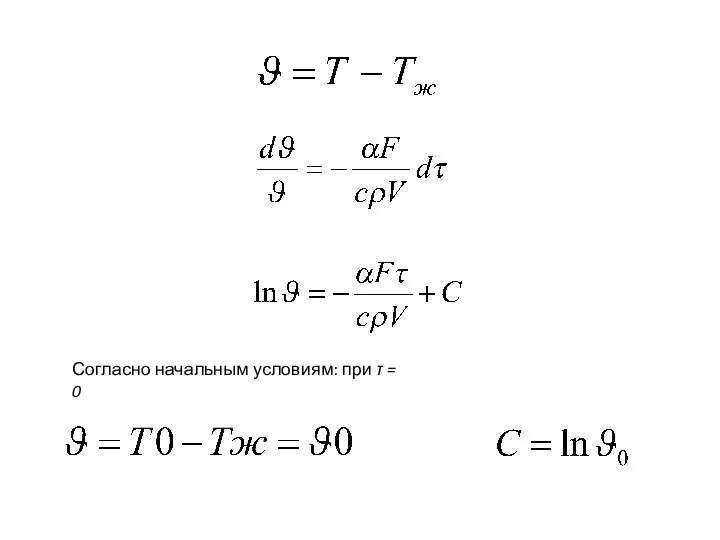

![m [1/сек] – темп охлаждения (нагревания). Характеризует интенсивность охлаждения (нагревания) тела. * **](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1182884/slide-101.jpg)


 Презентация на тему Потенциальная энергия
Презентация на тему Потенциальная энергия  Зубчатые передачи
Зубчатые передачи Ядерные реакции
Ядерные реакции Равенство работ при использовании простых механизмов. Золотое правило механики
Равенство работ при использовании простых механизмов. Золотое правило механики Физика в физкультуре
Физика в физкультуре Периодическое движение
Периодическое движение Ньютон. Совершенны ли законы Ньютона?
Ньютон. Совершенны ли законы Ньютона? Блоки. Простые механизмы
Блоки. Простые механизмы Элементы квантовой статистики
Элементы квантовой статистики Испарения и конденсация
Испарения и конденсация Тест Элементарные частицы
Тест Элементарные частицы Почему радуга разноцветная?
Почему радуга разноцветная? Презентация на тему Опыт по определению диаметра молекулы (11 класс)
Презентация на тему Опыт по определению диаметра молекулы (11 класс)  Исследование механических характеристик композитных материалов (КМ). Проектирование пакета слоёв
Исследование механических характеристик композитных материалов (КМ). Проектирование пакета слоёв Загадочные явления в Воде, на Земле, в Космосе. 7 класс
Загадочные явления в Воде, на Земле, в Космосе. 7 класс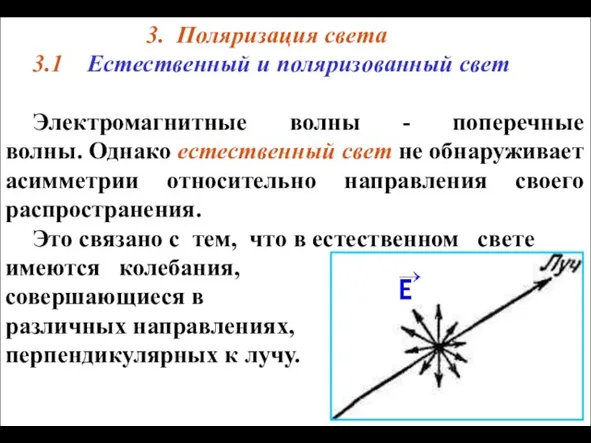 Поляризация света
Поляризация света Рубка металла
Рубка металла Технология обработки на металлорежущих станках. Контроль резьбовых поверхностей
Технология обработки на металлорежущих станках. Контроль резьбовых поверхностей Элементы теории относительности
Элементы теории относительности Определение длины световой волны с помощью дифракционной решетки. Лабораторная работа № 3. 11класс
Определение длины световой волны с помощью дифракционной решетки. Лабораторная работа № 3. 11класс Техническое обслуживание и текущий ремонт сцепления, коробки передач, карданной передачи
Техническое обслуживание и текущий ремонт сцепления, коробки передач, карданной передачи 1_kurs_2_nedelya (1)
1_kurs_2_nedelya (1) Радиационное излучение
Радиационное излучение Закон Ома и вычисление сопротивления. Решение задач
Закон Ома и вычисление сопротивления. Решение задач Теплотехнические измерения. Практическое занятие
Теплотехнические измерения. Практическое занятие Частицы вещества
Частицы вещества Elektrotekhnika_lektsia_1_VVEdenie_v_spetsialnost
Elektrotekhnika_lektsia_1_VVEdenie_v_spetsialnost Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц