Слайд 2Термодинамика излучения
Излучение находится в центре внимания физики.
Квантовая теория излучения представляет излучение как

поток фотонов – элементарных частиц.
Свойства фотонов
1 . Скорость фотонов равна скорости света.
2. Энергия фотона Е = hν.
h =6.626⋅10-34 Дж⋅с – постоянная Планка,
ν - частота излучения.
Слайд 3Термодинамика излучения
Одним из видов излучения является излучение нагретых тел.
«Нагретое тело» имеет любую

температуру, кроме 0 К.
Электромагнитное излучение, находящееся в равновесии с окружающими телами, называется тепловым, или равновесным.
Слайд 4Термодинамика излучения
Так как это излучение не выходит наружу, оно называется излучением абсолютно

черного тела.
Равновесное излучение в полости можно рассматривать как термодинамическую систему, обладающую
температурой (температура стенок), объемом (объем полости)
давлением
Излучение можно рассматривать как фотонный газ.
Слайд 8Термодинамика излучения
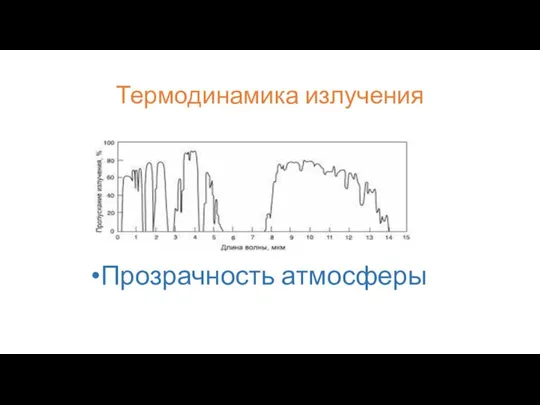
Прозрачность атмосферы
Слайд 9Взаимодействие излучения с веществом

Слайд 10Взаимодействие излучения с веществом

Слайд 11Взаимодействие излучения с веществом

Слайд 12Взаимодействие излучения с веществом

Слайд 13Взаимодействие излучения с веществом

Слайд 14Взаимодействие излучения с веществом

Слайд 15Взаимодействие излучения с веществом

Слайд 16Взаимодействие излучения с веществом

Слайд 17Взаимодействие излучения с веществом

Слайд 18Взаимодействие излучения с веществом

Слайд 19Взаимодействие излучения с веществом

Слайд 20Закон Стефана-Больцмана
Фотон поглощается стенкой.
Он передает стенке импульс, равный E/c, где E

– энергия фотона.
По принципу детального равновесия стенка должна испустить такой же фотон в том же направлении.
При этом она получит импульс отдачи также равный E/c.
Суммарный импульс, получаемый стенкой в результате взаимодействия с фотонным газом равен 2 E/c.
Слайд 27Начала молекулярно-кинетической теории
Экспериментальный материал термодинамику обобщает и систематизирует молекулярно-кинетическая теория.
Теория поддерживает

атомистическое мировоззрение,
Теория связывает воедино механику и термодинамику
Теория рассматривает обширный класс явлений, который невозможно ни объяснить, ни описать другими способами
Слайд 28Начала молекулярно-кинетической теории

Слайд 29Начала молекулярно-кинетической теории
Молекулярно-кинетическая теория опирается на законы механики – в первую очередь

на законы сохранения энергии и импульса.
В основе ее математического аппарата лежит теория вероятностей.
Слайд 30Элементы теории вероятностей
Событиями будем называть явления, которые в результате некоторого опыта могут

произойти или не произойти.
Если в данном опыте событие обязательно происходит, его называют достоверным, если оно не может произойти, его называют невозможным.
Слайд 31Элементы теории вероятностей
Вероятностью события это отношение опытов, в котором это событие произошло

к общему количеству опытов.
Подбросим вращающуюся монетку.
Равновозможных случая два или выпадение «орла» или «решки», и событие выпадения «орла» одно из равновозможных. Соответственно вероятность выпадения «орла» равна 1/2.
Таким образом вероятность выпадения «орла» дважды подряд, равна ¼, а вероятность выпадения хотя бы одного «орла» при двух бросаниях будет равна 3/4.
Слайд 32Элементы теории вероятностей
Пусть в коробке находится 35 красных, 40 зелёных и 25

белых шаров, всего их 100
Вероятность вынуть красный шар равна 35/100,
белый шар 1/4,
зелёный 4/10.
Лишь при достаточно большом числе испытаний получаемые результаты будут стремиться к указанным выше.
Слайд 34Элементы теории вероятностей
Случайной величиной называется величина, которая в результате опыта может принять

то или иное значение, причем неизвестно, какое именно.
Случайные величины бывают дискретными. Примером может служить число попаданий в мишень неподготовленным стрелком при десяти выстрелах.
Примером непрерывной случайной величины может служить расстояние от центра мишени при выстрелах.
Слайд 35Элементы теории вероятностей
Тот факт, что в результате опыта случайная величина приняла некоторое

значение есть событие, которое может характеризоваться вероятностью P.
Это – вероятность возможных значений дискретной случайной величины (для краткости говоря «вероятность величины X).
Сумма вероятностей всех значений дискретной случайной величины равна 1.
Слайд 36Элементы теории вероятностей
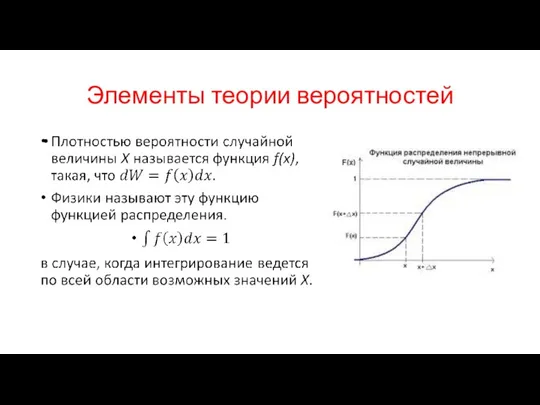
Законом распределения (или просто – распределением) случайной величины называется соотношение,

устанавливающее связь между значениями случайной величины и соответствующими им вероятностями.
Законом распределения дискретной случай величины называется таблица, в которой перечислены значения случайной величины и соответствующие им вероятности.
Слайд 37Элементы теории вероятностей
Тот факт, что в результате проведения опытов непрерывная случайная величина
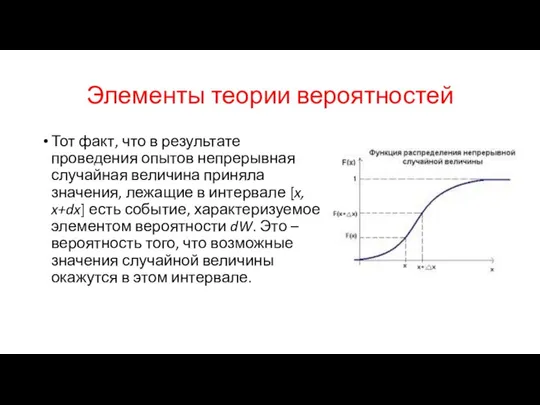
приняла значения, лежащие в интервале [x, x+dx] есть событие, характеризуемое элементом вероятности dW. Это – вероятность того, что возможные значения случайной величины окажутся в этом интервале.
Слайд 39Средние значения случайной величины
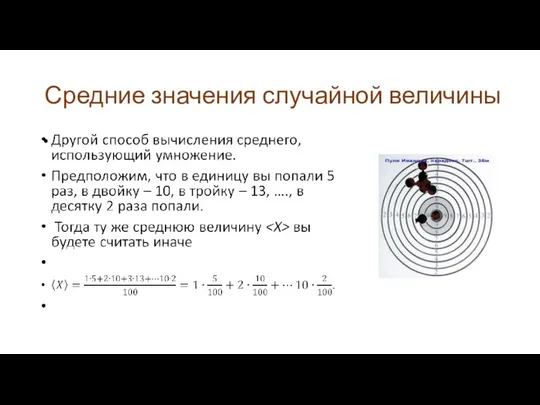
Вычисление средних по большому числу молекул значений различных величин:

скорости, энергии и т.д. является одной из задач молекулярно-кинетической теории.
Эта задача решается методами теории вероятностей.
Средние значения мы будем обозначать скобками - .
Слайд 40Средние значения случайной величины

Слайд 41Средние значения случайной величины
Слайд 42Средние значения случайной величины

Слайд 43Средние значения случайной величины

Слайд 44Идеальный газ с молекулярно-кинетической точки зрения
С точки зрения молекулярной теории идеальный газ

– это теоретическая модель газа, в которой пренебрегается взаимодействием между молекулами (за исключением взаимодействий в краткие моменты столкновений).
В воздухе, например, среднее расстояние между молекулами примерно в 103 больше их размера, поэтому очевидно, что при рассмотрении многих явлений взаимодействием молекул можно пренебречь.
Слайд 45Идеальный газ с молекулярно-кинетической точки зрения
Молекулы идеального газа находятся в основном в

состоянии равномерного и прямолинейного движения.
Все направления движения в отсутствие внешнего поля равновероятны.
Движение имеет хаотический характер, так как после каждого столкновения скорости и направления движения существенным образом меняются.
Слайд 46Направления движения молекул
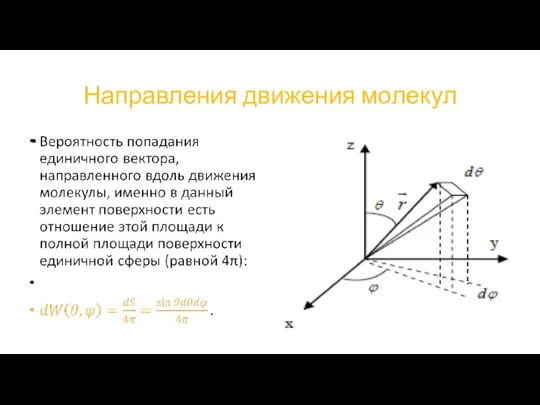
Выберем некоторое направление, характеризуемое углами θ и ϕ сферической системы

координат
Нас интересует доля молекул, движущихся именно в этом направлении
Можно говорить только о вероятности иметь направление в малых интервалах углов от θ до θ + dθ и от υ до υ + dυ. Эти углы задают в пространстве 4 направления
Слайд 47Направления движения молекул
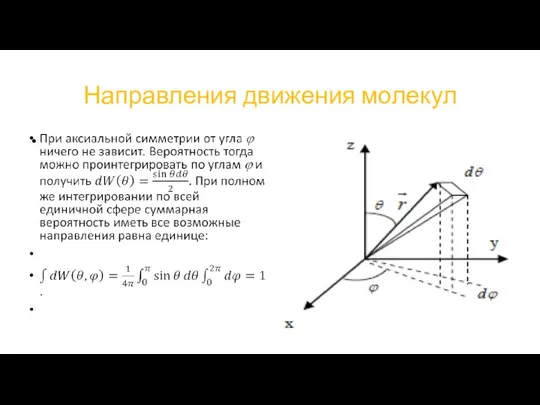
На единичной сфере задаваемые этими направлениями линии задают вершины криволинейного
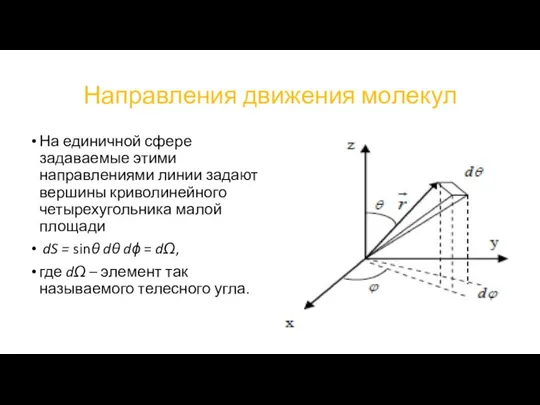
четырехугольника малой площади
dS = sinθ dθ dϕ = dΩ,
где dΩ – элемент так называемого телесного угла.
Слайд 53Давление идеального газа
Давление в сосуде с газом создается ударами молекул о его

стенку.
Будем считать удары абсолютно упругими.
Сначала рассмотрим удар одной молекулы.
Ось, перпендикулярную стенке, обозначим за х.
Слайд 54Давление идеального газа
При соударении стенка со стороны молекулы испытывает зависящую от времени
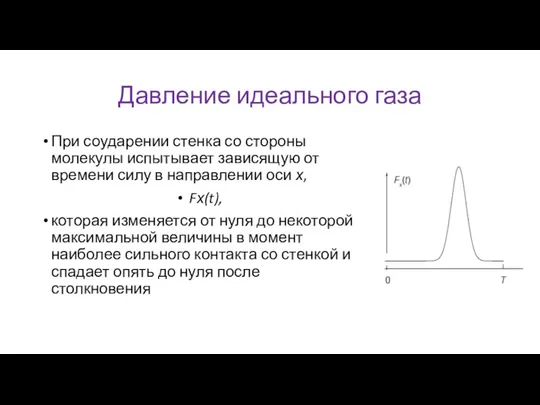
силу в направлении оси х,
Fх(t),
которая изменяется от нуля до некоторой максимальной величины в момент наиболее сильного контакта со стенкой и спадает опять до нуля после столкновения
Слайд 60Температура
Вопрос о связи температуры средней энергии молекул газа мы обсуждали в лекции

12.
«Если два тела с разной температурой привести в контакт, то рано или поздно их температуры станут равными.
Ровно то же самое произойдет со средней двух систем хаотически движущихся частиц, если так или иначе позволить им обмениваться энергией: средние энергии будут выравниваться.
Это наблюдение позволило высказать гипотезу о том, что температура пропорциональна средней кинетической энергии молекул.»


























































 Взаимные превращения жидкостей и газов
Взаимные превращения жидкостей и газов Комплексная механизация лесовосстановительных работ в Огудневском участковом лесничестве
Комплексная механизация лесовосстановительных работ в Огудневском участковом лесничестве Применение ядерной энергии. Развитие ядерной энергетики
Применение ядерной энергии. Развитие ядерной энергетики Ферромагнетики, антиферромагнетики, ферримагнетики, обменное взаимодействие
Ферромагнетики, антиферромагнетики, ферримагнетики, обменное взаимодействие Строение атома и атомного ядра. Использование энергии атомных ядер
Строение атома и атомного ядра. Использование энергии атомных ядер Задачи
Задачи Механическое оборудование для обработки мяса и рыбы. Лекция 5
Механическое оборудование для обработки мяса и рыбы. Лекция 5 Технология исследовательской деятельности в преподавании физики в рамках реализации ФГОС
Технология исследовательской деятельности в преподавании физики в рамках реализации ФГОС Проблема метода в философии права
Проблема метода в философии права Презентация на тему Основы термодинамики Решение задач
Презентация на тему Основы термодинамики Решение задач  Решение задач на вычисление массы продукта реакции по известной массе исходного вещества, содержащего примеси
Решение задач на вычисление массы продукта реакции по известной массе исходного вещества, содержащего примеси Джеймс Клерк (Кларк) Максвелл
Джеймс Клерк (Кларк) Максвелл ТО и ТР коробок передач
ТО и ТР коробок передач Презентация на тему Влияние радиоактивного излучения на живые организмы
Презентация на тему Влияние радиоактивного излучения на живые организмы  Презентация на тему Закон Паскаля
Презентация на тему Закон Паскаля  Динамика
Динамика Гидравлический домкрат в быту
Гидравлический домкрат в быту Зимний тепловой режим помещения. Лекция13
Зимний тепловой режим помещения. Лекция13 Физическая викторина
Физическая викторина Презентация на тему Напряженность электрического поля. Принцип суперпозиции электрических полей
Презентация на тему Напряженность электрического поля. Принцип суперпозиции электрических полей  Сила. Масса. Законы Ньютона 9 класс
Сила. Масса. Законы Ньютона 9 класс Александр Степанович Попов
Александр Степанович Попов Электромагниты
Электромагниты Светодиодная лампа. Открытый городской конкурс научно-технических проектов школьников Инженерный старт – 2019
Светодиодная лампа. Открытый городской конкурс научно-технических проектов школьников Инженерный старт – 2019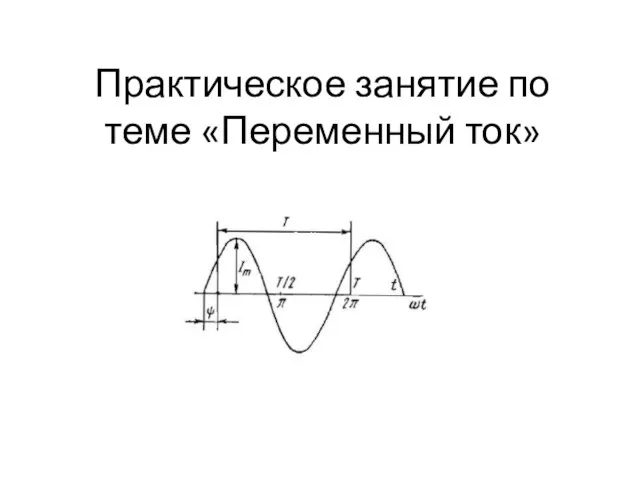 Переменный ток. Практическое занятие
Переменный ток. Практическое занятие Инновационная концепция электронного корабля
Инновационная концепция электронного корабля Термодинамика
Термодинамика Исследование эксплуатационных характеристик энергетической установки с ДВС 2Ч 8,5х11 при работе в газодизельном цикле
Исследование эксплуатационных характеристик энергетической установки с ДВС 2Ч 8,5х11 при работе в газодизельном цикле