Слайд 2Оглавление:
Введение. Понятие переменного тока.
2.1. Получение переменного тока.
2.2. Генератор переменного тока.
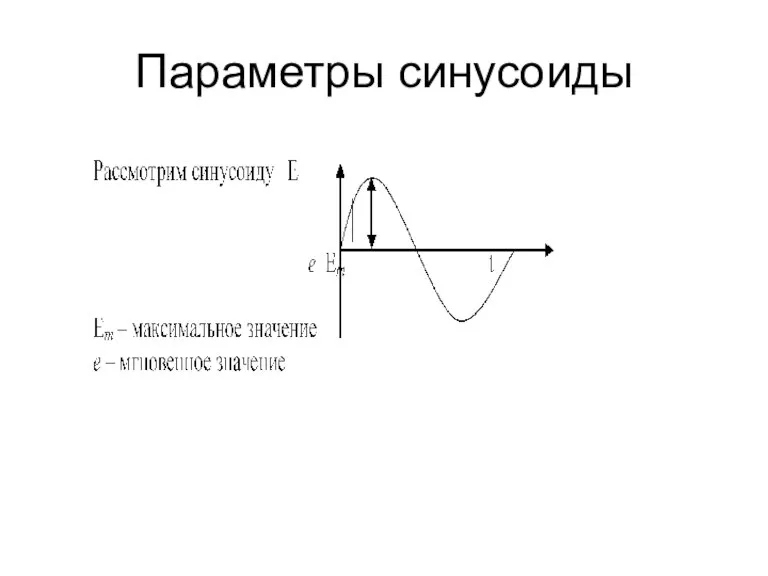
2.3. Параметры

синусоиды.
2.4. Действующее и среднее значение синусоидального тока.
2.5. Среднее значение синусоидального тока.
2.6. Представление синусоидальных величин в виде векторов. Векторные диаграммы.
2.7. Комплексная плоскость.
2.8. Законы Ома и Кирхгофа для цепей синусоидального тока.
Слайд 3Содержание темы
Широкое применение в электро- и радиоустановках находят периодические эдс, напряжения

и токи.
Периодические величины изменяются по величине и направлению во времени, причём эти изменения повторяются через равные промежутки времени Т, называемые периодом.
Переменный ток – это ток, изменяющийся во времени.
Синусоидальный ток – ток изменяющийся по закону синуса.
Слайд 4Цель лекции:
Изучить способ получения переменного тока, понять устройство генератора переменного тока

и принцип его работы. Изучить действующее и среднее значение синусоидального тока. Уметь представлять синусоидальные величины в виде векторов. Освоить символический метод расчета, а также законы Ома и Кирхгофа для цепей переменного тока и уметь применять их в расчетах.
Слайд 5После изучения вы сможете
Представлять синусоидальные величины в виде векторов. Применять в

расчетах символический метод расчета, а также законы Ома и Кирхгофа для цепей переменного тока.
Слайд 6Основное преимущество синусоидального тока
Основное преимущество такого закона изменения эдс и напряжения, заключается

в том, что в процессе передачи электроэнергии на большие расстояния и при многократной трансформации (изменении) напряжения. Его временная зависимость остается постоянной, т.е. синусоидальной. Как увидим дальше, передавать электроэнергию экономически выгодно высоким напряжением, а распределять из соображений безопасности низким. Поэтому и приходится его трансформировать.
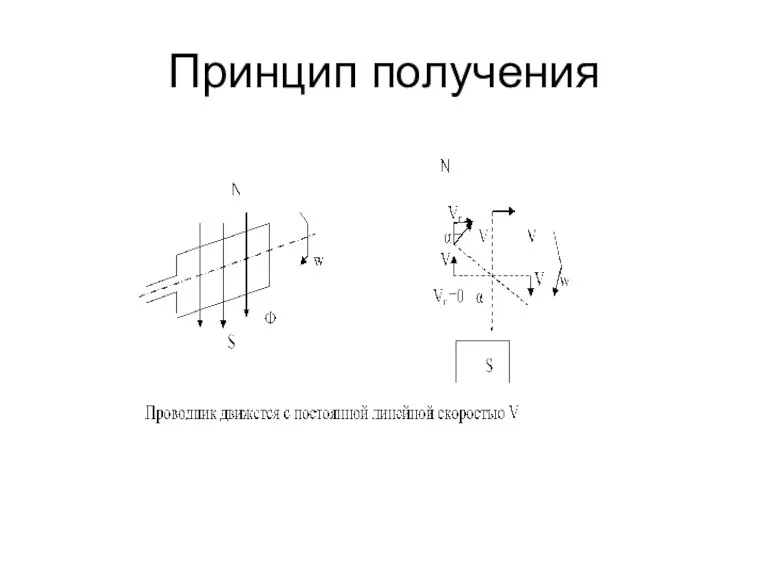
Слайд 7. Получение переменного синусоидального тока
Получение переменного тока основано на явлении электромагнитной

индукции. Рассмотрим вращение прямоугольного витка с угловой скоростью и помещенного в однородное магнитное поле с потоком Ф.
Слайд 9Получение синусоидальной ЭДС

Слайд 12. Генератор переменного тока
Переменный ток создают синхронные генераторы. Простейший синхронный генератор

состоит из неподвижной части – статора, и вращающейся – ротора.
Статор имеет форму полого цилиндра, в пазах которого уложены изолированные проводники, образующие обмотку статора.
Слайд 13Устройство генератора синусоидального тока

Слайд 14Магнитный поток
При вращении ротора создается магнитный поток, который пересекает проводники статора и

индуктирует в них переменную эдс: Φ = Φm cos ωt.
Слайд 16Период
Время одного полного оборота ротора называется периодом Т [сек].
Величина, обратная периоду, называется
![Период Время одного полного оборота ротора называется периодом Т [сек]. Величина, обратная](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1146153/slide-15.jpg)
частотой f = 1/T [1/сек] = [Гц] в системе СИ.
При полном обороте рамки α = 2π и α = ωТ, т.к. время t = Т.
Слайд 18Действующее значение синусоидального тока
Как постоянный, так и синусоидальный токи используются для

сКовершения какой-либо работы, в процессе которой эл. энергия преобразуется в другие виды энергий (тепловую, механическую и т.д.).
Для количественной оценки синусоидального тока пользуются действующим значением тока
Слайд 19Определение:
Действующим значением синусоидального тока называется такое значение постоянного тока, который за период

в одном и том же сопротивлении выделяет то же количество теплоты, что и рассматриваемый переменный ток.
Слайд 22Действующее значение
Действующее значение синусоидальной величины меньше максимального в раз.
Например, если Umax=141B, то

вольтметр покажет U=100В. Действующее значение измеряют приборы электромагнитной, электродинамической систем.
Слайд 24Среднее значение синусоидального тока
Под средним значением понимают среднеарифметическое значение синусоиды за

пол периода, т.к. за период оно будет равно нулю (положительные и отрицательные полуволны совпадают по форме).
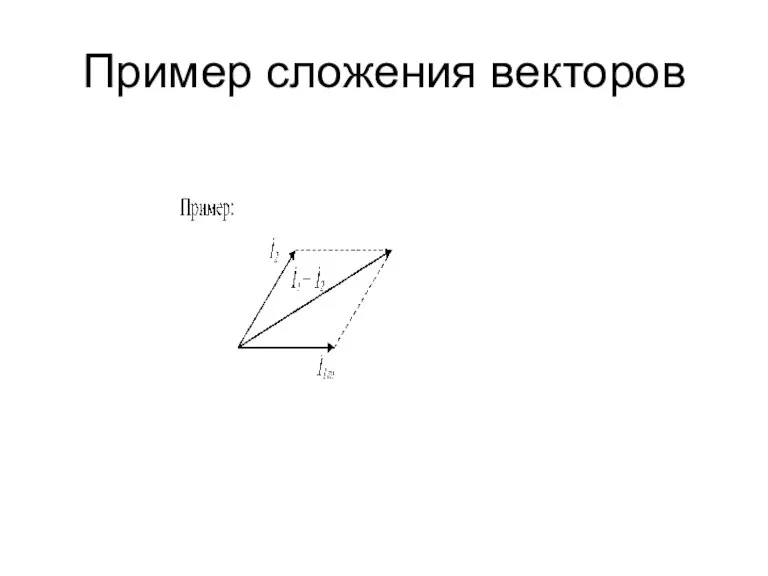
Слайд 27Представление синусоидальных величин в виде векторов
При расчете электрических цепей необходимо складывать

или вычитать синусоидальные величины. Графическое сложение двух (или более) таких величин является довольно трудоемкой операцией, а хорошая точность может быть достигнута при сложении очень большого числа мгновенных значений
Слайд 28Связь между вращающимся вектором и синусоидой

Слайд 31Связь между синусоидой и вектором
Между синусоидой и вектором существует строго однозначная связь

и любую синусоидально изменяющуюся величину можно изобразить вращающимся вектором. Начальное положение вращающегося вектора определяется углом, равным начальной фазе синусоиды.
Слайд 32Направление вращения вектора
Положительное направление вращения вектора принимается против часовой стрелки. Т.к. напряжения

и токи имеют одинаковую частоту, то изображающие их вектора вращаются с одинаковой скоростью. Их взаимное расположение в плоскости остается постоянным
Слайд 33Изображение векторов
Поэтому в практике векторы не вращают, а строят, соблюдая между ними

углы (углы сдвига фаз). (Комплексную плоскость также не рисуют.)
Слайд 34Векторная диаграмма
Совокупность векторов токов и напряжений, построенных в масштабе соблюдения фаз между

ними называются векторной диаграммой
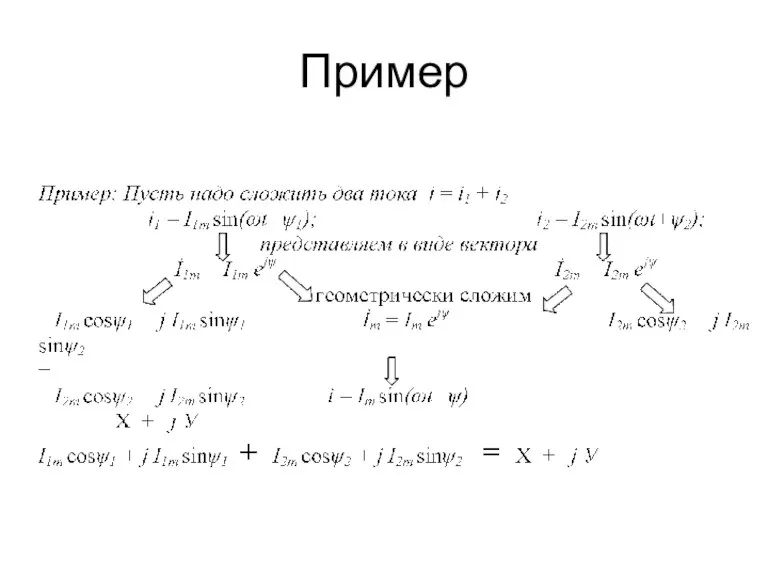
Слайд 39Математические операции над синусоидальными величинами
Математические операции над синусоидальными величинами можно проводить

в комплексной (векторной) форме. Докажем соответствие синусоидальной величины и её изображения на комплексной плоскости
Слайд 43Сложение и вычитание
Сложение и вычитание комплексных чисел удобнее проводить в алгебраической форме:
(a1+jb1)+(a2+jb2)-(a3+jb3)

= (a1+a2-a3) + j(b1+b2–b3)
Слайд 48Законы Ома и Кирхгофа для цепи синусоидального тока
Т.к. синусоидальные напряжения и

ток характеризуется мгновенными, максимальными и действующими значениями таким образом для каждого из них существует своя формулировка закона.
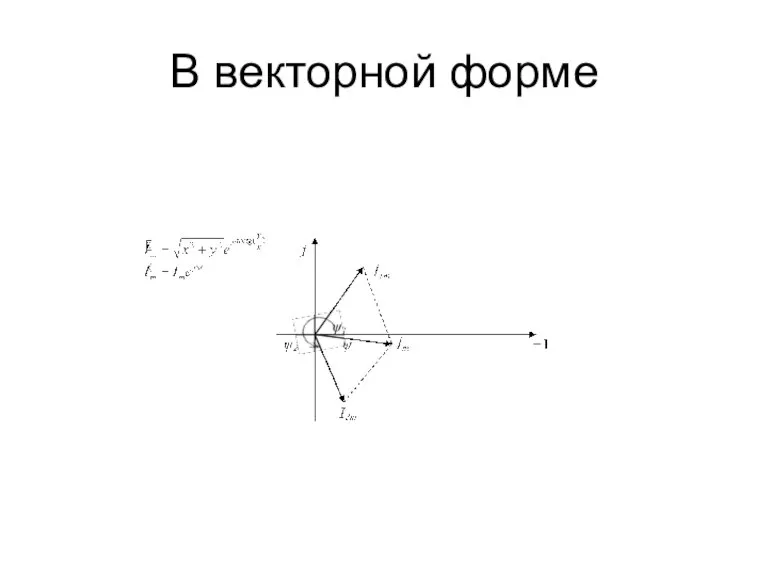
Для максимальных и действующих значений законы Ома и Кирхгофа справедливы в векторной форме:
Слайд 51Активное и реактивное сопротивление

Слайд 53Законы Кирхгофа для мгновенных значений













![Период Время одного полного оборота ротора называется периодом Т [сек]. Величина, обратная](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1146153/slide-15.jpg)
































![Комплексная проводимость [См]:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1146153/slide-51.jpg)


 Опыт Резерфорда. Строение атома. Спектр. Постулаты Бора
Опыт Резерфорда. Строение атома. Спектр. Постулаты Бора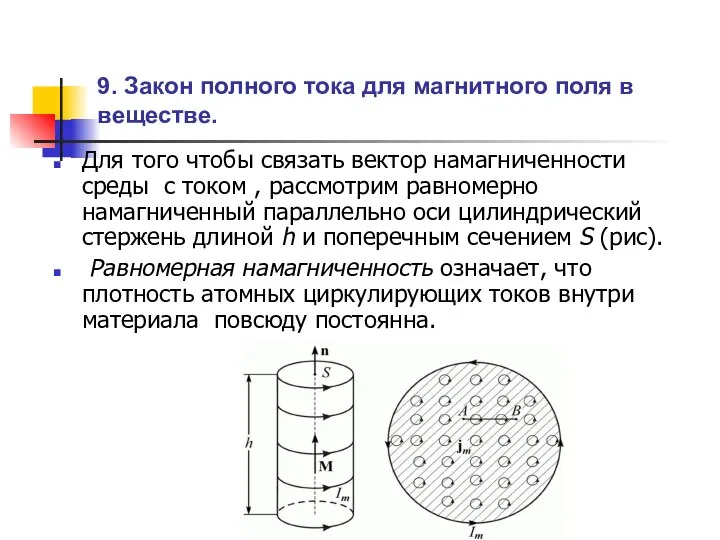 Закон полного тока для магнитного поля в веществе
Закон полного тока для магнитного поля в веществе Внутренняя энергия
Внутренняя энергия Презентация на тему Поверхностное натяжение жидкостей
Презентация на тему Поверхностное натяжение жидкостей  Физика ядра
Физика ядра Основы термодинамики. Тема № 4
Основы термодинамики. Тема № 4 Лекция 1 Ядерно-топливный цикл
Лекция 1 Ядерно-топливный цикл Чи довго пратимете
Чи довго пратимете Презентация на тему Скорости молекул. Опыт Штерна
Презентация на тему Скорости молекул. Опыт Штерна  Электризация тел
Электризация тел Измерение размеров малых тел
Измерение размеров малых тел Атмосферное давление. Решение экспериментальных задач
Атмосферное давление. Решение экспериментальных задач Опыты И. Ньютона и корпускулярная теория цвета
Опыты И. Ньютона и корпускулярная теория цвета Презентация на тему Магнитное поле
Презентация на тему Магнитное поле  Решение задач. Подготовка к контрольной работе
Решение задач. Подготовка к контрольной работе Теплотехника как наука
Теплотехника как наука Кинематика точки
Кинематика точки Напряженность электрического поля
Напряженность электрического поля Закона Кулона
Закона Кулона Концепции пространства и времени. Тема 5
Концепции пространства и времени. Тема 5 Презентация на тему Трансформаторы
Презентация на тему Трансформаторы  Движение и взаимодействие тел. Повторительно-обобщающий урок-игра
Движение и взаимодействие тел. Повторительно-обобщающий урок-игра Практикум по решению задач. Механическое движение
Практикум по решению задач. Механическое движение Период полураспада. Закон радиоактивного распада
Период полураспада. Закон радиоактивного распада Использование инфракрасного и оптического диапазонов радиоволн для передачи информации
Использование инфракрасного и оптического диапазонов радиоволн для передачи информации Бобрышев Анатолий Васильевич учитель физики Школа №30, г. Старый Оскол
Бобрышев Анатолий Васильевич учитель физики Школа №30, г. Старый Оскол Презентация на тему Третий закон Ньютона
Презентация на тему Третий закон Ньютона  Умная колонка на уроках физики
Умная колонка на уроках физики