Циркуляция вектора напряженности. Расчеты потенциальных полей. (Лекция 15)

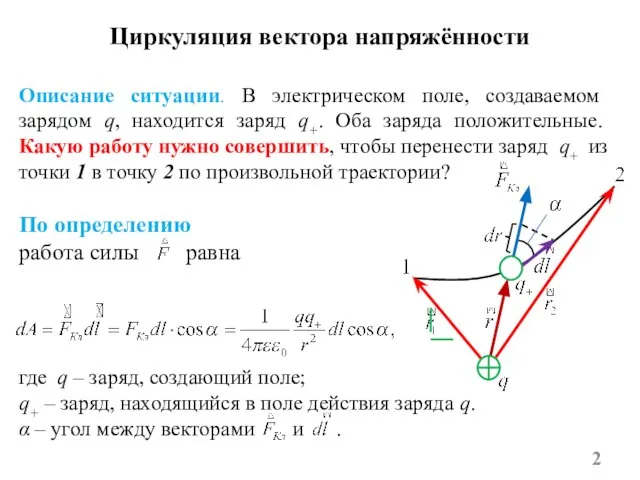
Циркуляция вектора напряжённости
Описание ситуации. В электрическом поле, создаваемом зарядом q, находится заряд q+. Оба заряда положительные. Какую работу нужно совершить, чтобы перенести заряд q+ из точки 1 в точку 2 по произвольной траектории?
где q – заряд, создающий поле;
q+ – заряд, находящийся в поле действия заряда q.
α – угол между векторами и .
По определению
работа силы равна

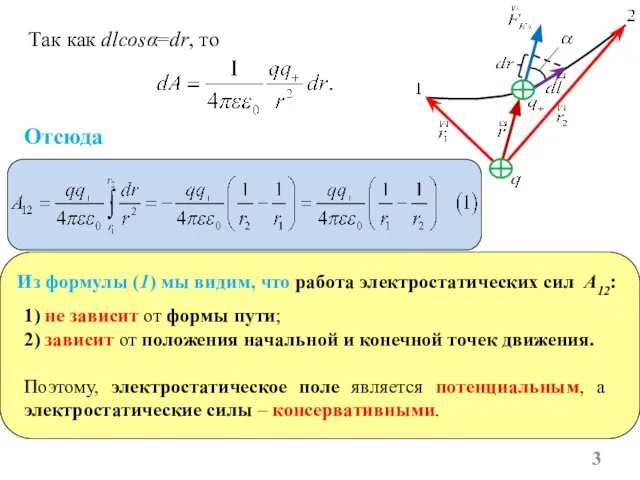
Так как dlcosα=dr, то
Из формулы (1) мы видим, что работа электростатических сил A12:
Отсюда
1) не зависит от формы пути;
2) зависит от положения начальной и конечной точек движения.
Поэтому, электростатическое поле является потенциальным, а электростатические силы – консервативными.

т.к.
3) будет равна нулю при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L (является следствием потенциальности электростатического поля).
то в соответствии с утверждением (2)
Поэтому

Интеграл (3) называется циркуляцией вектора напряжённости.
Таким образом,
Важно!
Любое силовое поле, обладающее свойством ,
называется потенциальным.
Циркуляция вектора напряжённости электростатического поля вдоль любого замкнутого контура равна нулю.
Теорема о циркуляции вектора напряжённости электростатического поля

Освежим воспоминания из раздела «Механика».
Вопрос №1. Что называется потенциальной энергией?
Ответ. Потенциальная энергия Ep – СФВ, являющаяся мерой взаимодействия тел или частей тела и зависящая от расстояния между ними.
Если в системе действуют потенциальные силы, то может быть определена некоторая функция координат взаимодействующих тел
Ep (x,y,z), которая называется потенциальной энергией системы.
Вопрос №2. Как формулируется теорема о потенциальной энергии?
Ответ. Убыль потенциальной энергии взаимодействия тел равна работе всех консервативных сил, действующих на тела системы в процессе перехода из начального состояния в конечное.

Вопрос №3. В чем особенность потенциальной энергии, что отличает её от кинетической энергии?
Ответ.
1) Потенциальная энергия определяется с точностью до произвольной постоянной С, значение которой зависит от выбора нулевого уровня потенциальной энергии.
2) Потенциальная энергия может иметь как положительное, так и отрицательное числовое значение.
Согласно уравнению (1)
Отсюда, с учётом уравнения (4)

Следовательно, потенциальная энергия взаимодействия двух точечных зарядов определяется выражением:
3) Потенциальная энергия взаимодействия одноименных зарядов (энергия отталкивания) положительна, а разноименных (энергия притяжения) – отрицательна. По мере уменьшения взаимного расстояния энергия взаимодействия (7) растет по модулю.
Важно!
1) Значение постоянной С зависит от выбора нулевого уровня потенциальной энергии.
2) Заряды, находящиеся на бесконечно большом расстоянии, не взаимодействуют, поэтому при r→∞ Ep(r→∞)=0, откуда С=0. В этом случае

Новый вопрос. Как определить потенциальную энергию заряда q0, находящегося в поле n зарядов?
Ответ. Если поле создаётся системой n точечных зарядов q1, q2,…, qn, то работа электростатических сил, совершаемая над зарядом q0, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия Ep заряда q0, находящегося в этом поле, равна сумме потенциальных энергий Epi, каждого из зарядов:

Потенциал φ электрического поля
Для характеристики полей удобно ввести в рассмотрение энергетическую характеристику – потенциал.
Различные пробные заряды q1, q2, … будут обладать в т. А различной потенциальной энергией.
Отношение не зависит от величины пробного заряда q+ и может служить энергетической характеристикой электрического поля в данной точке. Эта характеристика называется потенциалом φ электрического поля.
Обсудим уравнение*:
q – заряд, создающий поле;
r – расстояние от этого заряда до той точки поля A, в которой помещён пробный заряд q+.

Свойства потенциала.
Потенциал – величина алгебраическая (как и заряд q). Может быть положительной и отрицательной.
Числовое значение потенциала зависит от выбора нулевого уровня φ. Нулевой уровень потенциала – геометрическое место точек поля, потенциал которых принимается равным нулю. Выбирается произвольно.
Потенциал электрического поля φ – СФВ, энергетическая характеристика поля, равная потенциальной энергии, которой обладал бы в данной точке поля единичный положительный заряд.

Следовательно, потенциал электрического поля φ, созданного точечным зарядом q, в точке A равен:
Потенциал φ поля точечного заряда
Если поле создаётся точечным зарядом q, то пробный заряд q+ обладает в точке A потенциальной энергией (6).
Примем, что φ=0 при r→∞. Тогда С=0 и

Если поле создано совокупностью точечных зарядов q1, q2, … , qi, … qn , то его потенциал в т. А равен алгебраической сумме потенциалов φi создаваемых в т. А каждым из зарядов qi в отдельности:
Принцип суперпозиции для потенциала
Пример. Найти результирующий потенциал в точке B.

Множитель в (12) появился потому, что в результате суммирования энергий зарядов все парные взаимодействия оказались учтены дважды.
Энергия взаимодействия системы зарядов
- суммарный потенциал, создаваемый всеми зарядами, кроме qi , в точке, где помещается заряд qi

Пример. Найти энергию взаимодействия системы зарядов.

С учётом формулы (5)
т.е. работа, совершаемая силами электростатического поля при перемещении заряда q+ из точки 1 в точку 2 равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.
Работа, совершаемая силами электростатического поля

Представим (13) в виде
т.е. разность потенциалов между точками 1 и 2 - это скалярная физическая величина, равная работе сил электростатического поля по перемещению единичного (q+=1Кл) пробного заряда из точки 1 в точку 2.
Разность потенциалов между двумя точками равняется 1В, если при перемещении пробного заряда в 1Кл из одной точки в другую силы электрического поля совершают работу 1Дж.
Важный нюанс! При решении конкретных задач физический смысл имеет разность потенциалов между двумя точками электростатического поля.

Мы знаем, что сила электрического взаимодействия является консервативной. Эта сила взаимосвязана с потенциальной энергией:
Напряжённость как градиент потенциала
откуда
Необходимо: найти взаимосвязь между напряжённостью электростатического поля – силовой характеристикой поля и потенциалом – энергетической характеристикой поля.
где
- полный дифференциал (потенциальная энергия зависит только от начального и конечного положения тела, и не зависит от пути, по которому происходи переход)

Для полного вектора получим
Таким образом, убыль потенциальной энергии взаимодействия зарядов, приходящаяся на единицу длины данного направления, численно равная проекции силы на это направление.
Вспомним, что
Градиентом называется векторная характеристика скалярного поля; вектор градиента направлен в сторону наиболее быстрого возрастания скалярной величины в пространстве.

Фундаментальная связь между потенциалом и напряженностью электрического поля: вектор напряженности поля равен взятому с обратным знаком градиенту потенциала:
Важно!
1. Однозначная связь между напряженностью и потенциалом говорит об эквивалентности описания полей как путем задания напряженностей, так и путем задания потенциалов.
2. Напряженность поля равна градиенту потенциала со знаком «–». Знак «–» определяется тем, что вектор напряженности поля всегда направлен в сторону быстрейшего убывания потенциала электрического поля.

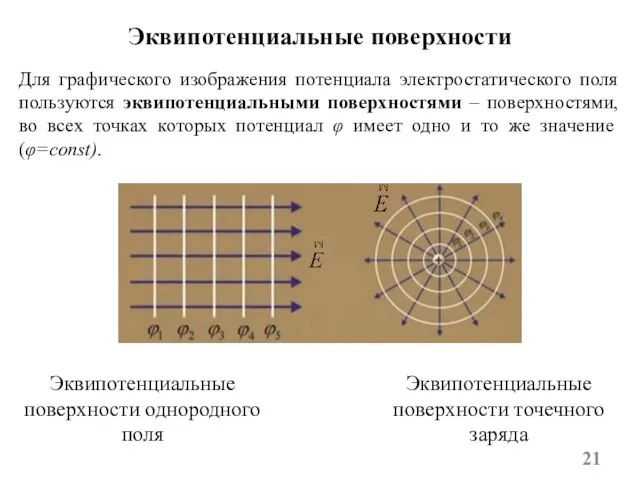
Эквипотенциальные поверхности
Для графического изображения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал φ имеет одно и то же значение (φ=const).
Эквипотенциальные поверхности однородного поля
Эквипотенциальные поверхности точечного заряда

Выводы
1. Работа сил эл. ст. поля при перемещении заряда по ней равна нулю .
Все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т.е. электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям.
2. Следовательно, вектор всегда нормален к эквипотенциальным поверхностям, поэтому линии вектора ортогональны к этим поверхностям.

3) Эквипотенциальные поверхности не пересекаются.
4) «Густота» эквипотенциальных поверхностей пропорциональна модулю , т.е. она характеризует пространственное распределение потенциала.
Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше.

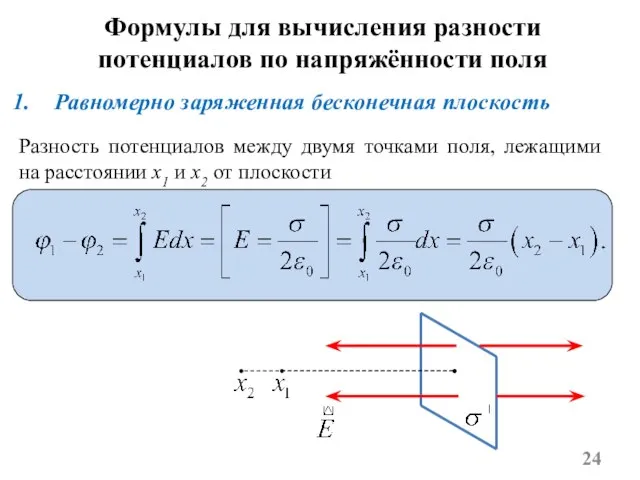
Равномерно заряженная бесконечная плоскость
Формулы для вычисления разности потенциалов по напряжённости поля
Разность потенциалов между двумя точками поля, лежащими на расстоянии x1 и x2 от плоскости

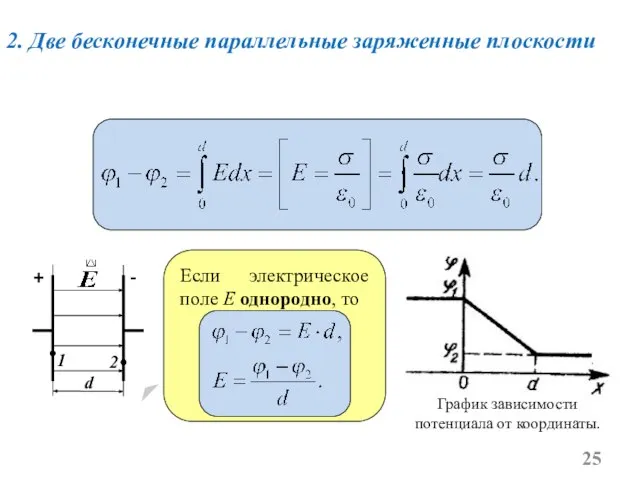
2. Две бесконечные параллельные заряженные плоскости
График зависимости
потенциала от координаты.
Если электрическое поле E однородно, то

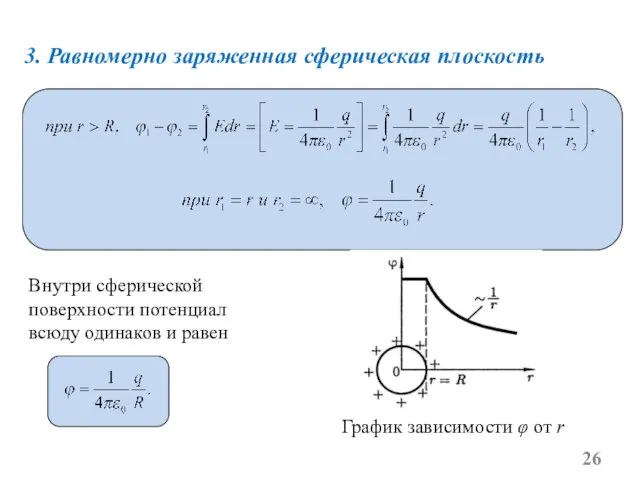
3. Равномерно заряженная сферическая плоскость
График зависимости φ от r
Внутри сферической поверхности потенциал всюду одинаков и равен

4. Объёмно заряженный шар
где r1 и r2 – расстояния от центра шара.