Содержание
- 2. Лекция 21 μ- пространство. Распределения Максвелла по скоростям и Больцмана по энергиям. Колебательные и вращательные суммы
- 3. Энтропия в каноническом ансамбле. Найдите правильную формулу: 3. 2. 1. 4. 1 балла
- 4. Характеристическая температура, θ. Найдите правильное утверждение. 4. Характеризует расстояние между уровнями энергии, в джоулях ! 3.
- 5. В системе А-В установилось фазовое равновесие жидкий раствор-пар и все химические равновесия. В паре обнаружены молекулы
- 6. Число компонентов системы – это минимальное число независимых химических частиц, которое необходимо для описания состава всех
- 7. Средняя кинетическая энергия и средняя скорость молекул в идеальном газе. Найдите верные утверждения! 4. Средняя энергия
- 8. Для расчета суммы по состояниям Q существуют формулы (1) и (2) которой из них нужно пользоваться?
- 9. Чем мембранное равновесие отличается от фазового? Найдите верные утверждения! 2 балла
- 11. Сумма по состояниям для колебательного движения
- 12. Уровни колебательной энергии
- 13. Колебательная сумма по состояниям 2-х атомной молекулы
- 14. Колебательная сумма Zкол и термодинамические функции
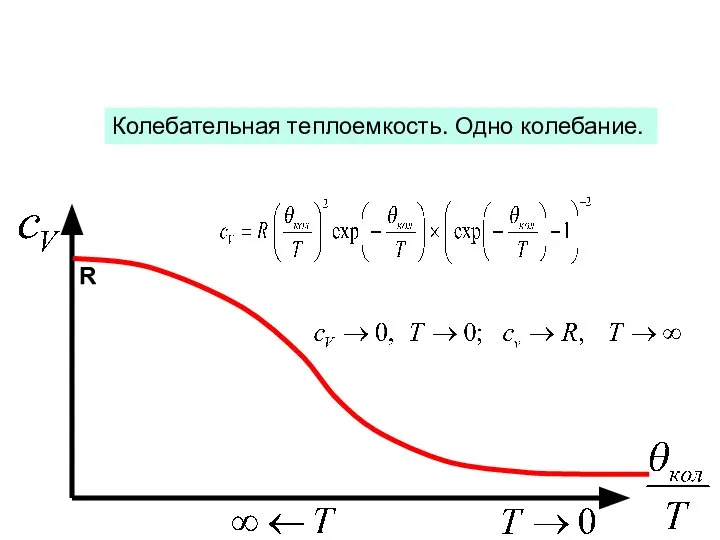
- 15. R Колебательная теплоемкость. Одно колебание.
- 16. Статистический расчет теплоемкости кристаллов (атомных кристаллов).
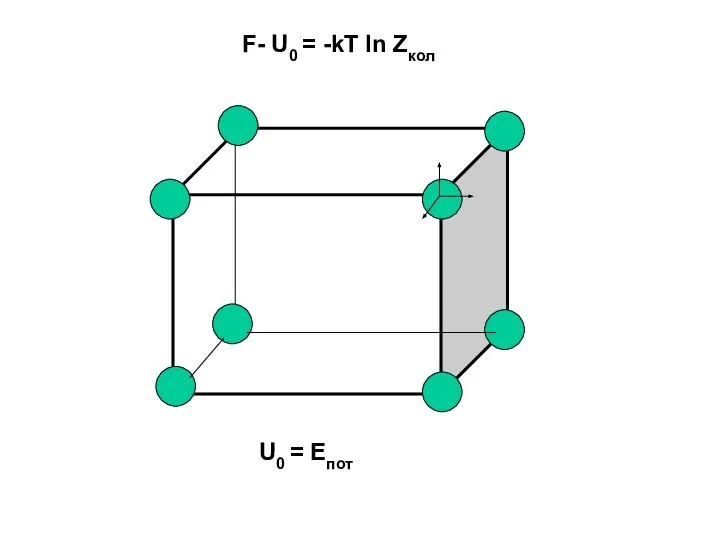
- 18. F- U0 = -kT ln Zкол U0 = Eпот
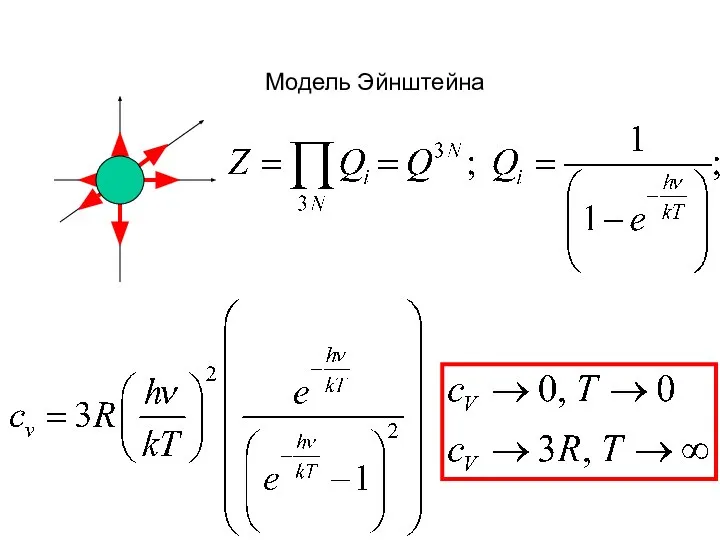
- 19. Модель Эйнштейна
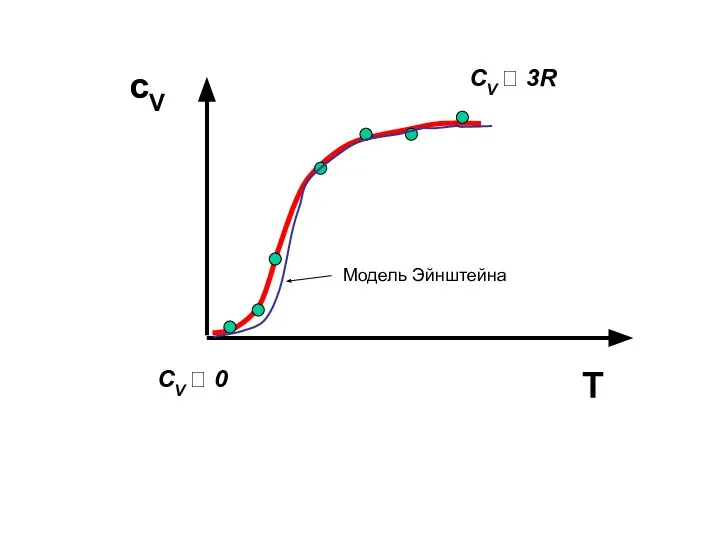
- 20. сV T Модель Эйнштейна СV ? 0 СV ? 3R
- 21. Модель Дебая
- 22. Модели Дебая и Эйнштейна. Обе модели позволяют рассчитать теплоемкость кристаллов Обе модели рассчитывают энергию кристалла E
- 23. Модель Дебая
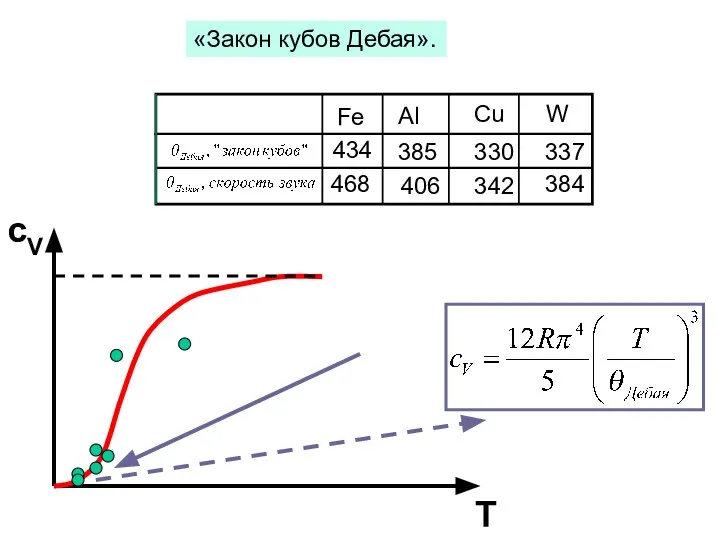
- 24. сV T «Закон кубов Дебая». Fe Al Cu W 434 385 330 337 468 406 342
- 25. Поиски новых способов оценки теплоемкости кристаллов
- 26. Теплоемкость молекулярных кристаллов
- 27. Вращательная и ядерная суммы по состояниям.
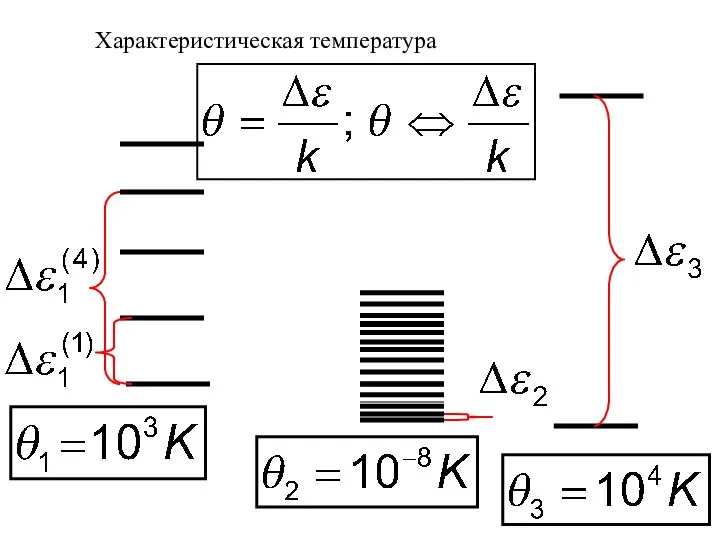
- 28. Характеристическая температура
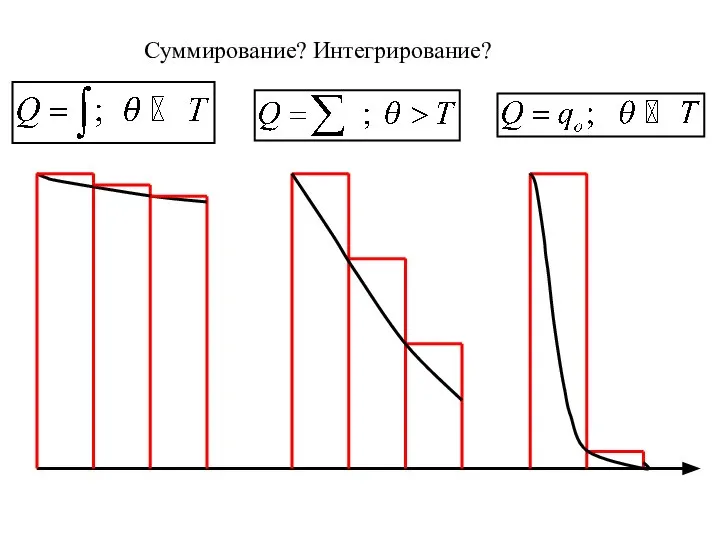
- 29. Суммирование? Интегрирование?
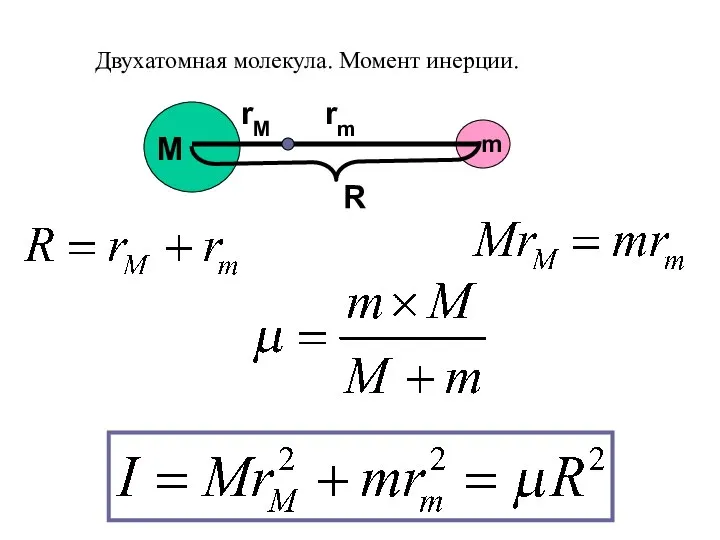
- 30. M m rm rM R Двухатомная молекула. Момент инерции.
- 31. Двухатомная молекула. Вращательное движение
- 32. J=0 J=1 J=2 gвр = 1 gвр= 5 gвр = 3 Уровни вращательной энергии
- 33. Вращательная сумма двухатомной молекулы
- 34. Вращательная сумма двухатомной молекулы
- 35. Вращательная сумма двухатомной молекулы. Вклад в термодинамические функции.
- 36. Вращательная сумма для многоатомной молекулы. Нелинейная молекула: Линейная молекула:
- 37. Вращательная сумма для многоатомной молекулы. Вклад в термодинамические функции Нелинейная молекула: Линейная молекула:
- 38. Внутреннее вращение
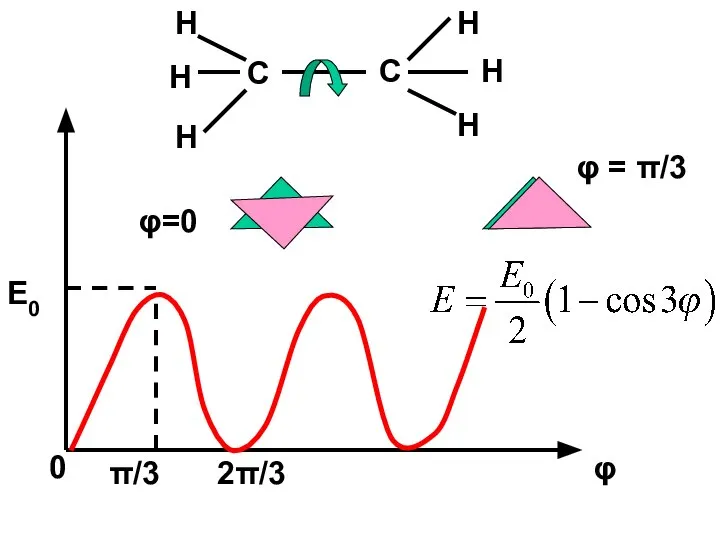
- 39. C H H H C H H H φ=0 φ = π/3 2π/3 π/3 φ 0
- 40. Сумма по состоянию для внутреннего вращения Число степеней свободы: 3 пост. +3(2) вр. +вв. +(3N-6(5)-вв.) кол.
- 41. Ядерные и вращательные суммы по состоянию
- 42. Ядерные суммы по состояниям Для атома: Для молекулы: Для химической реакции:
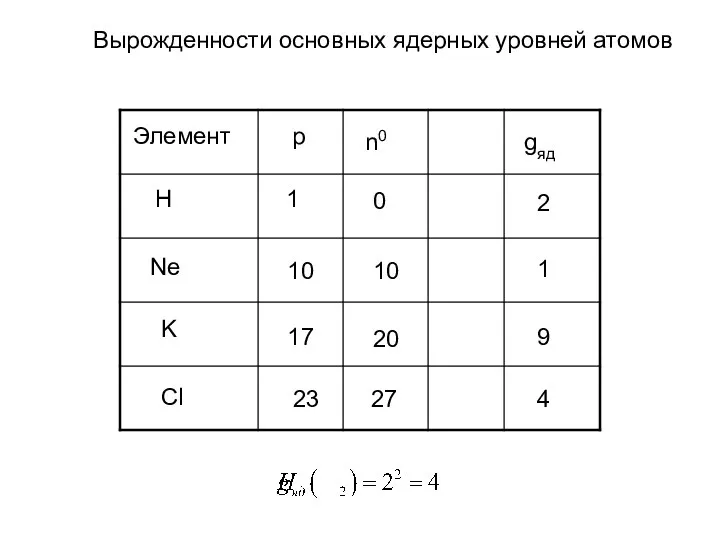
- 43. Элемент gяд H Ne K Cl p n0 1 10 17 0 10 20 23 27
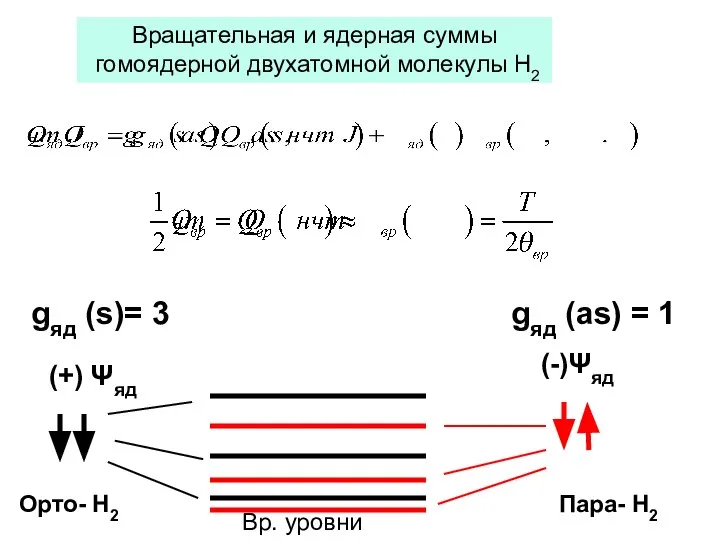
- 44. Вращательная и ядерная суммы гомоядерной двухатомной молекулы А2 Для молекулы из ядер с нечетной массой :
- 45. Вращательная и ядерная суммы гомоядерной двухатомной молекулы А2 Для молекулы из ядер с нечетной массой :
- 46. (-)Ψяд (+) Ψяд gяд (s)= 3 gяд (as) = 1 Пара- Н2 Орто- Н2 Вр. уровни
- 47. Орто- Н2 (Qяд(s), Qвр(as, J=1,3….) Пара- Н2 Qяд( as), Qвр(s, J=0,2….) Пара- и орто-водород при низких
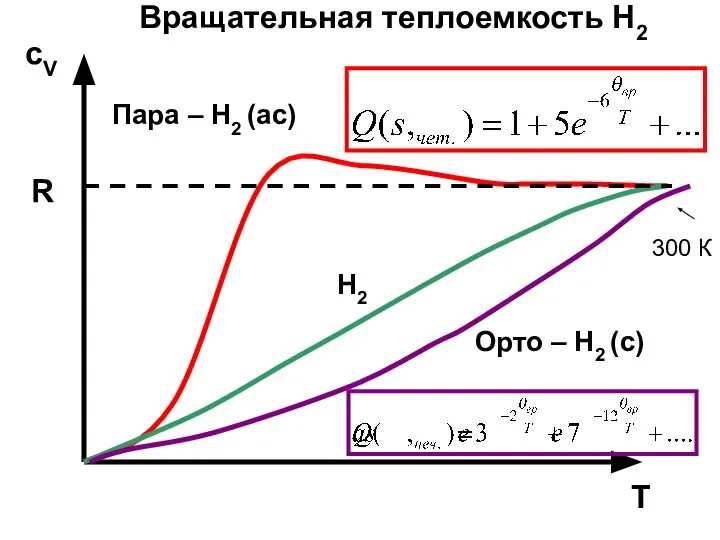
- 48. R cV T H2 Орто – Н2 (с) Пара – Н2 (ас) Вращательная теплоемкость Н2 300
- 49. Расчет термодинамических функций
- 51. Скачать презентацию




































 Измерение температуры вещества в зависимости от времени при изменениях агрегатных состояний
Измерение температуры вещества в зависимости от времени при изменениях агрегатных состояний Давление газов. Закон Паскаля
Давление газов. Закон Паскаля Газы
Газы Механическая работа. Энергия
Механическая работа. Энергия Презентация на тему Гравитационные силы
Презентация на тему Гравитационные силы  Теоретическая механика. Кинематика
Теоретическая механика. Кинематика Электростатика. Фальгурит
Электростатика. Фальгурит Презентация на тему Электричество в доме (8 класс)
Презентация на тему Электричество в доме (8 класс)  М. В. Ломоносов. Его вклад в развитие физики
М. В. Ломоносов. Его вклад в развитие физики Формообразование на станках
Формообразование на станках Элементарные частицы. Античастицы
Элементарные частицы. Античастицы Таблицы и графики
Таблицы и графики ОМиУОИ_л1
ОМиУОИ_л1 Виды энергии
Виды энергии Материальная точка Путь. Перемещение СО
Материальная точка Путь. Перемещение СО Импульс материальной точки
Импульс материальной точки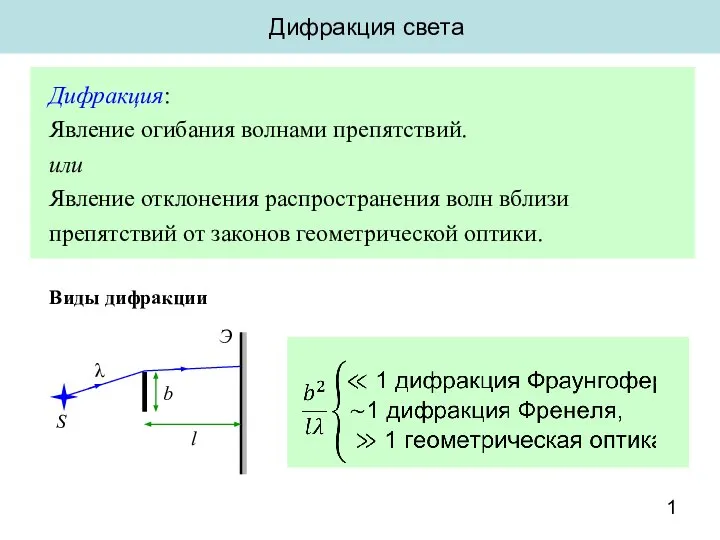 Дифракция света
Дифракция света Устройства ввода информации
Устройства ввода информации Явление фотоэффекта
Явление фотоэффекта Презентация на тему Переменный электрический ток (11 класс)
Презентация на тему Переменный электрический ток (11 класс)  Свободные и вынужденные электромагнитные колебания
Свободные и вынужденные электромагнитные колебания Электрический ток. Источники электрического тока
Электрический ток. Источники электрического тока Кипение. Парообразование
Кипение. Парообразование Кристаллические и аморфные тела
Кристаллические и аморфные тела Изотопы. Разновидности атомов одного ХЭ, отличающиеся друг от друга числом нейтронов в ядре
Изотопы. Разновидности атомов одного ХЭ, отличающиеся друг от друга числом нейтронов в ядре Презентация на тему Скорость света
Презентация на тему Скорость света  Плавание судов. Воздухоплавание
Плавание судов. Воздухоплавание Как научиться решать задачи по физике
Как научиться решать задачи по физике