Слайд 2ЗАДАЧИ
1. Тело переместилось из точки с координатами Х=0 м, У=2

м в точку координатами Х1=4 м, У1=1м. Сделать чертёж, найти перемещение и его проекции на оси координат.
2. Вертолет, пролетав в горизонтальном полёте по прямой 40 км, повернул под углом 90 градуса и пролетав еще 30 км. Найти путь и перемещение вертолета.
3. Движение двух велосипедистов заданы уравнениями: Х=5t,
Х1=150-10t. Найти время и место встречи.
1
Слайд 3РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
Движение по наклонной плоскости
Свободное падение тел
Движение под действием силы трения

Слайд 4УСКОРЕНИЕ
– характеристика неравномерного движения, показывает на сколько изменилась скорость за 1с.
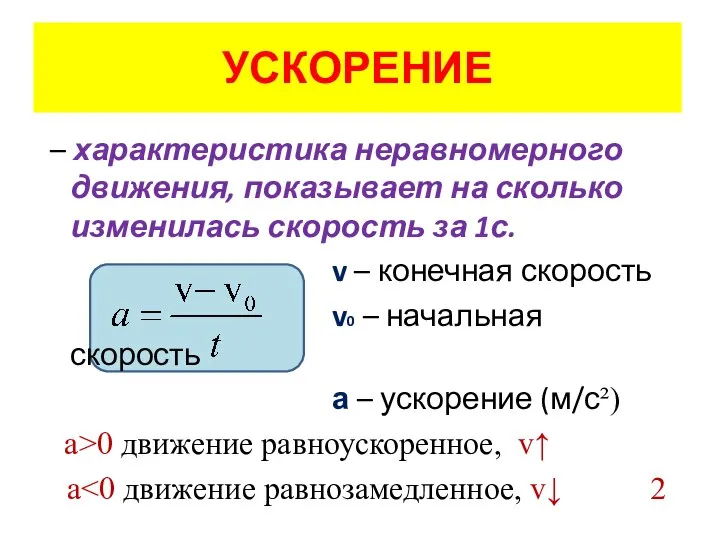
v – конечная скорость
v0 – начальная скорость
а – ускорение (м/с²)
а>0 движение равноускоренное, v↑
a<0 движение равнозамедленное, v↓ 2
Слайд 6Задача
Велосипедист движется под уклон с ускорением 0,3 м/с2. какую скорость приобретет велосипедист

через 20 с, если его начальная равна 4 м/с
Слайд 7Если мгновенная скорость неравномерного движения изменяется одинаково за любые равные промежутки времени,

то это движение называется движением с постоянным ускорением или равноускоренным движением
Слайд 11ЗАДАЧА
Уравнение координаты тела имеет вид
x = 20 + 5t - t²
а) опишите

характер движения тела
б) найдите начальную координату, модуль и направление начальной скорости и ускорения
в) напишите уравнение зависимости скорости от времени
г) найдите координату, путь и скорость тела через 3 с
д) постройте графики скорости и ускорения от времени
Слайд 12РЕШЕНИЕ
а) опишите характер движения тела
движение равноускоренное, т.к. есть слагаемое содержащее

квадрат времени
x = 20 + 5t - t²
Слайд 13РЕШЕНИЕ
б) найдите начальную координату, модуль и направление начальной скорости и ускорения
Сравним

два уравнения
х = 20 + 5t - t² и x = x0 + v0t +at²/2 х0 = 20м, v0 = 5м/с (вдоль оси ОХ, т.к. v0 >0)
а = - 2м/с² (против ОХ, т.к. а < 0)
Слайд 14РЕШЕНИЕ
в) напишите уравнение зависимости скорости от времени
Уравнение скорости: v = v0

+ at
Подставим: v0 = 5, а = - 2
v = 5 – 2t
Слайд 15РЕШЕНИЕ
г) найдите координату, путь и скорость тела через 3 с
x(3) =

20 + 5·3 – 3² = 20 +15 – 9 = 26
v(3) = 5 – 2·3 = - 1
(I способ)
s(3) = |x(3) – x(0)| s(3) = 26 – 20 = 6
(II способ) s = v0t +at²/2
s(3) = 5·3 – 9 = 6
Слайд 16РЕШЕНИЕ
д) постройте графики скорости и ускорения от времени
v = 5 –
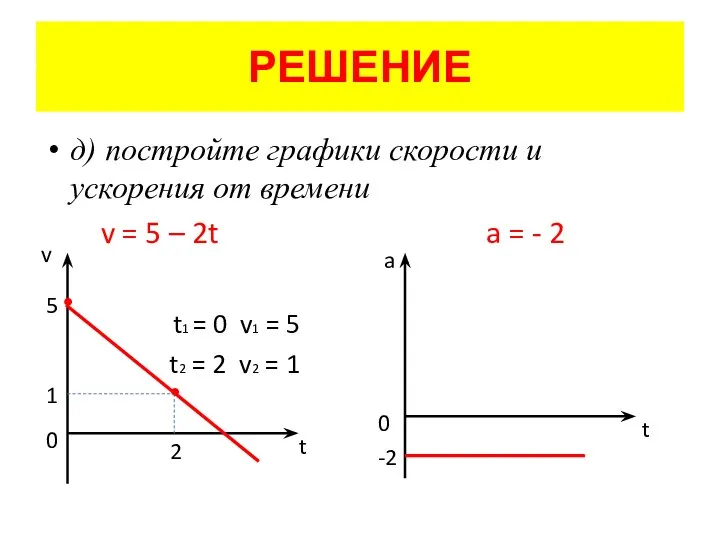
2t a = - 2
t1 = 0 v1 = 5
t2 = 2 v2 = 1
●
5
●
1
0
2
v
t
a
0
-2
t













 Аналогия между механическими и электромагнитными колебаниями
Аналогия между механическими и электромагнитными колебаниями ДИНАМИКА в задачах (1)
ДИНАМИКА в задачах (1) Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al
Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al Радиоактивность. Виды радиоактивных излучений и методы их регистрации
Радиоактивность. Виды радиоактивных излучений и методы их регистрации Электростатика вакуума и проводников
Электростатика вакуума и проводников Термодинамика негіздері
Термодинамика негіздері Инструкция по технике безопасности труда в кабинете физики
Инструкция по технике безопасности труда в кабинете физики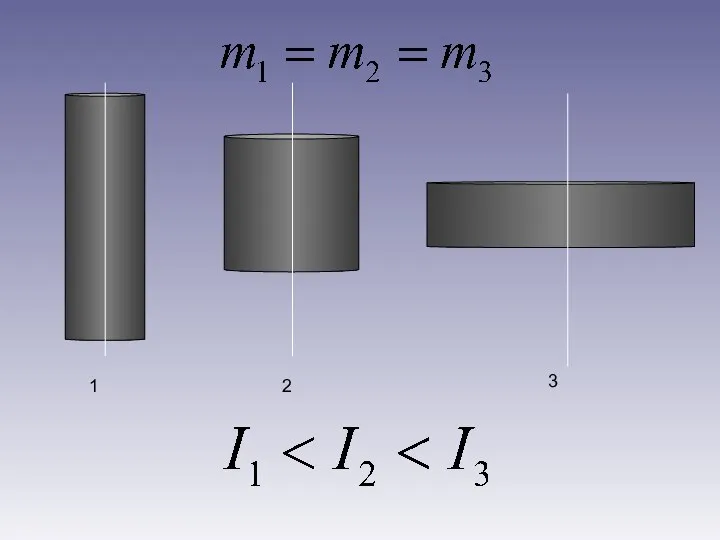 Закон сохранения момента импульса
Закон сохранения момента импульса Оптика, квантовая и ядерная физика. Лекция 14-15
Оптика, квантовая и ядерная физика. Лекция 14-15 Машина и её основные части
Машина и её основные части Поршневой компрессор. Лабораторная работа
Поршневой компрессор. Лабораторная работа Основные и дополнительные средства защиты в сетях напряжением выше 1000 в
Основные и дополнительные средства защиты в сетях напряжением выше 1000 в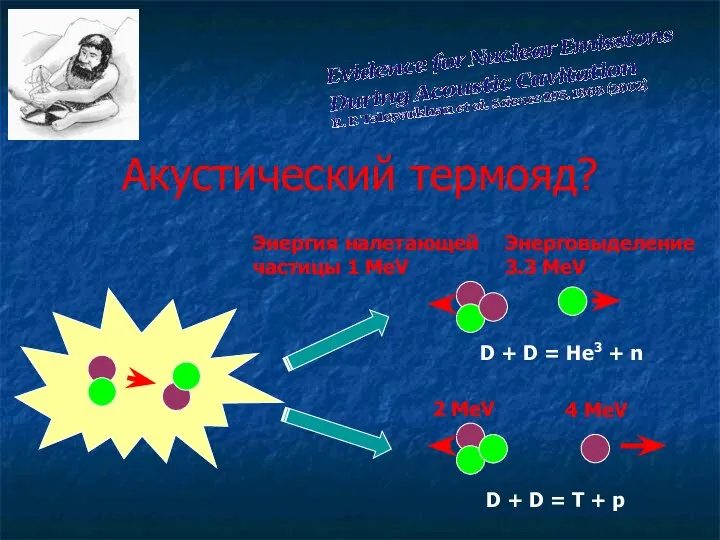 Акустический термояд
Акустический термояд Дисперсия света
Дисперсия света Электрический ток в различных средах
Электрический ток в различных средах Попов – основатель радиовещания
Попов – основатель радиовещания Лекция 16 ДОПУСКИ и ПОСАДКИ (1)
Лекция 16 ДОПУСКИ и ПОСАДКИ (1)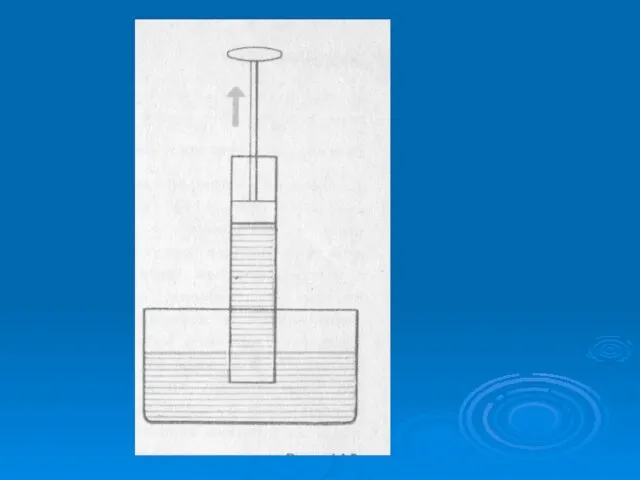 Презентация на тему Гидравлический пресс
Презентация на тему Гидравлический пресс  Графический материал к выпускной квалификационной (бакалаврской) работе на тему: Электроснабжение части села кучугуры
Графический материал к выпускной квалификационной (бакалаврской) работе на тему: Электроснабжение части села кучугуры Отчёт о проверке автомобиля
Отчёт о проверке автомобиля Сообщающиеся сосуды (урок физики, 7 класс)
Сообщающиеся сосуды (урок физики, 7 класс) Знатоки физики О, сколько нам открытий чудных Готовит просвещенья дух И опыт, сын ошибок трудных И гений, парадоксов дру
Знатоки физики О, сколько нам открытий чудных Готовит просвещенья дух И опыт, сын ошибок трудных И гений, парадоксов дру Презентация по физике "Что? Где? Когда?" -
Презентация по физике "Что? Где? Когда?" -  Физические величины и их измерение. Задания
Физические величины и их измерение. Задания Архимедова сила. Решение задач
Архимедова сила. Решение задач Элементарная теория атома водорода по бору
Элементарная теория атома водорода по бору Электризация тел. Взаимодействие заряженных тел
Электризация тел. Взаимодействие заряженных тел Абсорбционная спектроскопия (поглощение света веществом)
Абсорбционная спектроскопия (поглощение света веществом)