Установочные лекции для студентов заочного отделения

Контрольная работа
При изучении курса физики обучающиеся выполняют две контрольные работы. В втором семестре необходимо сдать контрольную работу №2, в которой необходимо решить восемь задач по темам дисциплины того варианта, номер которого совпадает с последней цифрой шифра зачетной книжки студента. Номера задач для каждого варианта приведены в табл. 1.3 учебного пособия.
Для выполнения задания требуются:
Л.В. Гулин, С.В. Анахов. Задачи по курсу физики: учебно-методическое пособие. Екатеринбург: Изд-во Рос. гос. проф.-пед. ун-та, 2015. 104 с.

Литература:
1. Трофимова Т.И. Курс физики: учеб. пособие для инженерно-технич. специальностей вузов - М.: Академия, 2010.
2. Савельев И.В. Основы теоретической физики: учебник в 3 томах. 3-е изд., - СПб. : Издательство "Лань", 2005.
3. Чертов А.Г. Задачник по физике: учеб. пособие для втузов / А.Г. Чертов, А.А. Воробьёв. - 9-е изд., перераб. и доп. - М. : изд. Физико-математической литературы, 2009.
4. Трофимова Т.И. Сборник задач по курсу физики для втузов / Т.И. Трофимова, 3-е изд. - М. : Оникс 21 век; Мир и образование, 2005.

Магнитные взаимодействия
Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад.
Он появился в Европе приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле. Первыми экспериментами, показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда (1820 г.).
Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся повернуть стрелку.

Теорема о циркуляции вектора В
Теорема о циркуляция вектора В: циркуляция вектора В по произвольному контуру равна произведению μ0 на алгебраическую сумму токов, охватываемых контуром:
Причем Ik – величины алгебраические. Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта. Ток противоположного направления считается отрицательным.
Используя эту теорему можно показать, что магнитное поле соленоида

Магнитная индукция характеризует силовое действие магнитного поля на ток (аналогично,
характеризует силовое действие электрического поля на заряд).
– силовая характеристика магнитного поля, ее можно изобразить с помощью магнитных силовых линий.

АМПЕР Андре Мари (1775 – 1836) – французский физик математик и химик.
Основные физические работы посвящены электродинамике. Сформулировал правило для определения действия магнитного поля тока на магнитную стрелку. Обнаружил влияние магнитного поля Земли на движущиеся проводники с током.
Закон Ампера

В 1820 г. А. М. Ампер экспериментально установил, что два проводника с током взаимодействуют друг с другом с силой:
где b – расстояние между проводниками, а k – коэффициент пропорциональности зависящий от системы единиц.
В первоначальное выражение закона Ампера не входила никакая величина характеризующая магнитное поле. Потом разобрались, что взаимодействие токов осуществляется через магнитное поле и следовательно в закон должна входить характеристика магнитного поля.

В современной записи в системе СИ, закон Ампера выражается формулой:
Это сила с которой магнитное поле действует на бесконечно малый проводник с током I.
Модуль силы действующей на проводник

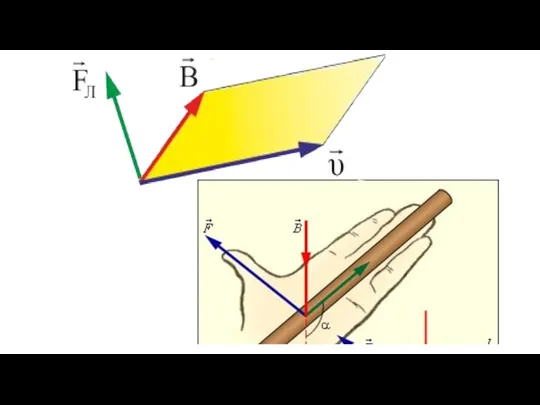
Направление силы определяется направлением векторного произведения или правилом левой руки (что одно и тоже). Ориентируем пальцы по направлению первого вектора, второй вектор должен входить в ладонь и большой палец показывает направление векторного произведения.
Закон Ампера – это первое открытие фундаментальных сил, зависящих от скоростей.

Сила Ампера
П Р А В И Л О
левой руки

Из закона Ампера хорошо виден физический смысл магнитной индукции: В – величина, численно равная силе, с которой магнитное поле действует на проводник единичной длины, по которому течет единичный ток.
Размерность индукции

Сила Лоренца

Модуль лоренцевой силы:
,
где α – угол между и .
Из формулы видно, что на заряд, движущийся вдоль линии , не действует сила ( ).
Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат векторы и . К движущемуся положительному заряду применимо правило левой руки или
«правило буравчика»

Направление действия силы для отрицательного заряда – противоположно, следовательно, к электронам применимо правило правой руки.
Так как сила Лоренца направлена перпендикулярно движущемуся заряду, т.е. перпендикулярно , работа этой силы всегда равна нулю. Следовательно, действуя на заряженную частицу, сила Лоренца не может изменить кинетическую энергию частицы.
Часто лоренцевой силой называют сумму электрических и магнитных сил:
здесь электрическая сила ускоряет частицу, изменяет ее энергию.

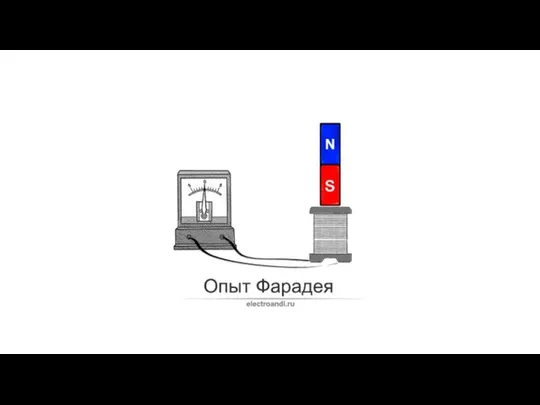
ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Фарадей М. в 1831 г. экспериментально открыл тот факт, что изменяющееся со временем магнитное поле, пронизывающее проводящий контур, индуцирует в нем электрический ток. Данное явление было названо явлением электромагнитной индукции. На основании опытных данных был сформулирован закон электромагнитной индукции:
Электродвижущая сила индукции, порожденная изменением магнитного потока через поверхность, которую ограничивает замкнутый контур, пропорциональна скорости изменения магнитного потока взятой с обратным знаком
Знак «–» в данном выражении объясняет правило Ленца:
Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызвавшей.

ЯВЛЕНИЕ самоИНДУКЦИИ
В случае, когда магнитный поток создается током текущим в проводящем контуре, изменения данного тока I приводит к изменению полного магнитного потока и в контуре индуктируется ЭДС. Такое явление называется самоиндукцией, а ЭДС – ЭДС самоиндукции. Если рассматриваемый контур состоит из N витков, то результирующая ЭДС равна сумме ЭДС, индуцируемых в каждом из витков в отдельности, т.е.
где – потокосцепление или полный магнитный поток.
Откуда электромагнитная индукция
Очевидно, что с точностью до коэффициента L, который называют индуктивностью контура. Значит

Единицей индуктивности в СИ является Гн – генри. 1 Гн – это индуктивность контура с током 1А, который создает полный магнитный поток через поверхность ограниченную данным контуром величиной 1 Вб.

Из понятия потокосцепления следует, что индуктивность длинного соленоида
где V – объем соленоида.
ЭДС самоиндукции записывается выражением
Если выполняется условие, что индуктивность контура не меняется со временем, то

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Будем считать, что ключ К переводят из 1 в 2. При этом ток возрастает согласно экспоненциального закона от 0 А до I0. Сила тока в цепи по закону Ома
Полная работа источника тока за время dt равна
Второе слагаемое последней суммы определяется индукционными явлениями в цепи. Значит соответствующая данному слагаемому полная работа при увеличении тока в цепи от 0 А до I0 равна

Данная работа источника тока идет на увеличение энергии магнитного поля в контуре, а значит энергия магнитного поля равна
Учитывая, что магнитное поле длинного соленоида однородно, можно разделить последнее выражение на объем соленоида и получить объемную плотность магнитного поля:

ТОК СМЕЩЕНИЯ
Между обкладками конденсатора линии тока проводимости обрываются и ток как бы «исчезает в никуда» и «появляется из ничего», что противоречит закону сохранения. Поэтому логично предположить, что линии тока проводимости в конденсаторе переходят в линии другого тока. Этот другой ток назвали током смещения, его плотность равна:
Таким образом, ток смещения – это переменное электрическое поле.
Плотность полного тока тогда должна быть равна:

УРАВНЕНИЯ максвелла в интегральной форме
1
2
3
4

УРАВНЕНИЯ максвелла в интегральной форме
Материальные уравнения:

Колебательные процессы
Колебание – изменение состояния системы по периодическому или почти периодическому закону: маятник часов, груз на пружине, гитарная струна, давление воздуха в звуковой волне.
Виды колебаний
Свободные (или собственные) колебания: колебания в системе, предоставленной самой себе:
шарик в лунке, маятник.
Вынужденные колебания – колебания под действием внешней периодической силы: вибрации моста, качели.

Механические колебания
Свободные незатухающие гармонические колебания.
Пружинный маятник
mx” = - kx ⇨ mx” + kx = 0 ⇨
x” + ω02x = 0 – дифференциальное уравнение гармонических колебаний (ω02 = k/m)
x = Acos(ω0t + φ0) – гармоническое колебание
A – амплитуда колебаний
ω0 – циклическая частота
φ0 – начальная фаза
ω0t + φ0 – фаза колебаний
T = 2π/ ω0 – период колебаний
Изохронность: ω0 – определяется только свойствами системы и не зависит от амплитуды.
F = -kx – квазиупругая возвращающая сила

Скорость и ускорение при гармонических колебаниях
Смещение:
x = Acos(ω0t + φ0)
Скорость:
v = x’ = - ω0Asin(ω0t + φ0) = ω0Acos(ω0t + φ0 + π/2);
v0 = ω0A – амплитуда скорости;
скорость опережает смещение x по фазе на π/2.
Ускорение
a = - ω02Acos(ω0t + φ0) = ω02Acos(ω0t + φ0 + π)
a0 = ω02A – амплитуда ускорения;
ускорение в противофазе со смещением

Энергия гармонических колебаний
Потенциальная энергия:
П = kx2/2 = ½kA2cos2(ω0t + φ0)
Кинетическая энергия:
K = mv2/2 = ½mω02A2sin2(ω0t + φ0) =
½кA2sin2(ω0t + φ0)
Полная энергия:
Е = П + K = const = ½kA2 = ½mv02
Для гармонических колебаний:
= <П> = ½E

Затухающие колебания.
Сила вязкого трения Fтр = -βv
mx” = - kx – βv ⇨ mx” + βv + kx = 0 ⇨
x” + 2γx’ + ω02 x = 0 - дифференциальное уравнение колебаний с затуханием;
γ = β/2m – коэффициент затухания
ω02 = k/m – собственная частота
если γ < ω0,то
x = а0e-γtcos(ωt + φ0),
ω = (ω02 – γ2)1/2 – частота затухающих колебаний; а0e-γt – амплитуда затухающих колебаний

Характеристики затухающих колебаний
Время релаксации τ – это время, за которое амплитуда колебаний уменьшается в e раз:
τ = 1/ γ
Логарифмический декремент затухания:
λ = ln[a(t)/a(t + T)] = γT = T/τ
Число колебаний, за которое амплитуда уменьшается в e раз
Ne = τ/T = 1/λ
Слабое затухание Ne = τ/T = ω/2πγ >> 1 ⇨
γ << ω ≈ ω0

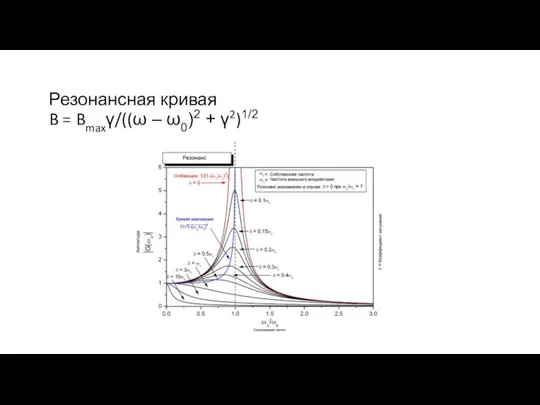
Вынужденные колебания. Резонанс.
mx” + βv + kx = Fcosωt ⇨
x” + 2γx’ + ω02x = fcos ωt, f = F/m
Уравнение вынужденные колебания имеет вид:
x = Bcos(ωt + φ)
где амплитуда
B = f/((ω2 – ω02)2 + 4γ2ω2)1/2
Фаза
tg φ = 2γω/(ω02– ω2)
В резонансе (при малых γ)
Bmax ≈ B(ω0) = f/2γω0 ⇨ Bmax/Bстат = ω0/2γ = Q
Вблизи резонанса:
B = Bmaxγ/((ω – ω0)2 + γ2)1/2 ⇨ ширина резонансной кривой Δω = 2γ

Резонансная кривая
B = Bmaxγ/((ω – ω0)2 + γ2)1/2

Электромагнитные колебания.
Свободные электромагнитные колебания.
Электрический колебательный контур. Формула Томсона.
Электромагнитные колебания могут возникать в цепи, содержащей индуктивность L и емкость C. Такая цепь называется колебательным контуром. Возбудить колебания в таком контуре можно, например, предварительно зарядив конденсатор от внешнего источника напряжения, соединить его затем с катушкой индуктивности.
Поскольку внешнее напряжение к контуру не приложено, сумма падений напряжений на емкости и индуктивности должна быть равна нулю в любой момент времени:
откуда, учитывая, что сила тока , получаем дифференциальное уравнение свободных незатухающих колебаний электрического заряда в колебательном контуре
.

Если ввести обозначение
,
то полученное уравнение принимает вид:
.
Решением этого уравнения, как известно, является функция
.
Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ω0, называемой собственной частотой колебательного контура. Период колебаний определяется по формуле Томсона (Thomson W., 1824-1907):
Напряжение на конденсаторе:
,
где - амплитуда напряжения.
Сила тока в контуре:
.

Сопоставляя полученные выражения, видим, что когда напряжение на конденсаторе, а значит энергия электрического поля, обращается в нуль, сила тока, а, следовательно, энергия магнитного поля, достигает максимального значения. Таким образом, электрические колебания в контуре сопровождаются взаимными превращениями энергий электрического и магнитного полей.
Амплитуды тока Im и напряжения Um связаны между собой очевидным соотношением:
.

Аналогия процессов свободных электрических и механических колебаний

Свободные затухающие колебания. Добротность колебательного контура.
Всякий реальный колебательный контур обладает сопротивлением. Энергия электрических колебаний в таком контуре постепенно расходуется на нагревание сопротивления, переходя в джоулево тепло, вследствие чего колебания затухают.
Уравнение свободных затухающих колебаний можно получить, исходя из того, что в отсутствии внешнего источника напряжения, сумма падений напряжений на индуктивности, емкости и сопротивлении равна нулю для любого момента времени:
или, поскольку ,
.
Введя обозначение
,
этому уравнению можно придать вид:
.

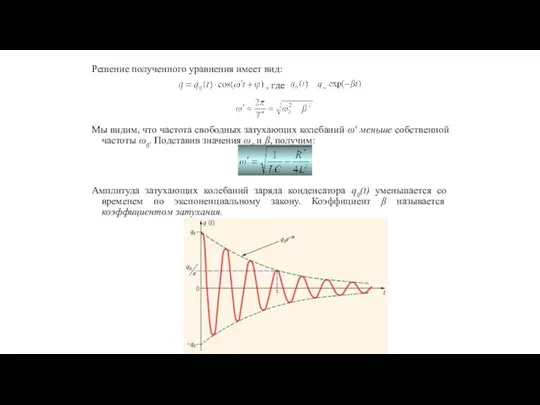
Решение полученного уравнения имеет вид:
, где
Мы видим, что частота свободных затухающих колебаний ω′ меньше собственной частоты ω0. Подставив значения ω0 и β, получим:
Амплитуда затухающих колебаний заряда конденсатора q0(t) уменьшается со временем по экспоненциальному закону. Коэффициент β называется коэффициентом затухания.

Затухание колебаний принято характеризовать декрементом колебаний λ, определяемым как:
.
Легко видеть, что декремент колебаний обратен по величине числу колебаний Ne, совершаемых за время, в течение которого амплитуда колебаний уменьшается в е раз: λ=1/Ne. Добротностью колебательного контура называется величина:
Из этой формулы видно, что добротность тем выше, чем меньше коэффициент затухания β. При малых затуханиях (λ<<1) можно приближенно считать, что
.
Амплитуда тока в контуре, как и заряд на конденсаторе, убывает со временем по закону e-βt. Энергия W, запасенная в контуре, пропорциональна квадрату амплитуды тока (или квадрату напряжения на конденсаторе). Следовательно, W убывает со временем по закону e-2βt. Относительное уменьшение энергии за период колебания Т (при малом затухании) есть:
.
Таким образом, потери энергии в колебательном контуре тем меньше, чем выше его добротность.

Вынужденные электрические колебания
Если в цепь электрического контура, содержащего емкость, индуктивность и сопротивление, включить источник переменной ЭДС, то в нем, наряду с собственными затухающими колебаниями, возникнут незатухающие вынужденные колебания. Частота этих колебаний совпадает с частотой изменения переменной ЭДС.
Чтобы получить уравнение вынужденных колебаний, надо, согласно второму правилу Кирхгофа, приравнять сумму падений напряжений на элементах контура приложенной ЭДС:
или
где Е0 - амплитуда переменной ЭДС; ω – ее циклическая частота.

Интересующее нас частное решение этого дифференциального уравнения имеет вид:
где
Решение соответствующего однородного уравнения, как мы видели в п.5.2, представляет собой свободные затухающие колебания, которые с течением времени становятся исчезающе малыми, и их можно в дальнейшем не учитывать.
Выпишем формулы для силы тока в цепи и падений напряжений на каждом из элементов контура.
Сила тока: ,
.
По аналогии с законом Ома для полной цепи по постоянному току величину
называют полным сопротивлением цепи по переменному току. Эта величина представляет собой модуль комплексного сопротивления ,
называемого также импедансом цепи. Сопротивление R называют активным сопротивлением (на нем выделяется тепло). Чисто мнимые сопротивления ωL и называют соответственно индуктивным и емкостным реактивными сопротивлениями (на них тепло не выделяется).

Напряжение на сопротивлении R:
, .
Напряжение на конденсаторе С:
, .
Напряжение на катушке индуктивности L:
, .
Сравнивая написанные формулы, видим, что изменение напряжения на сопротивлении следует за изменением силы тока в цепи без отставания или опережения по фазе, изменение напряжение на конденсаторе отстает по фазе на , а на индуктивности опережает по фазе на изменение тока.

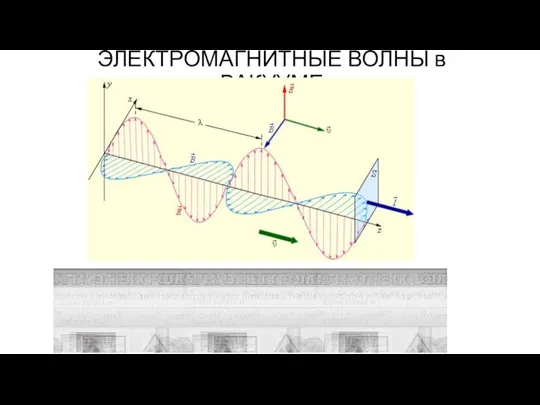
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ в ВАКУУМЕ

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ в ВАКУУМЕ
Э/м волны поперечны
Э/м волны распространяются со скоростью
Объемные плотности электрического и магнитного полей равны друг другу
Э/м волны переносят энергию. Например, через площадку S за малое время
Δt будет перенесена энергия:

ОПТИКА
Развитие взглядов на природу света
Исаак Ньютон
корпускулярная теория
(свет – поток частиц)
Христиан Гюйгенс
волновая теория
(свет – волна)
17 век
19 век
Джеймс Кларк Максвелл – электромагнитная природа света
20 век
Макс Планк – квантовая природа света

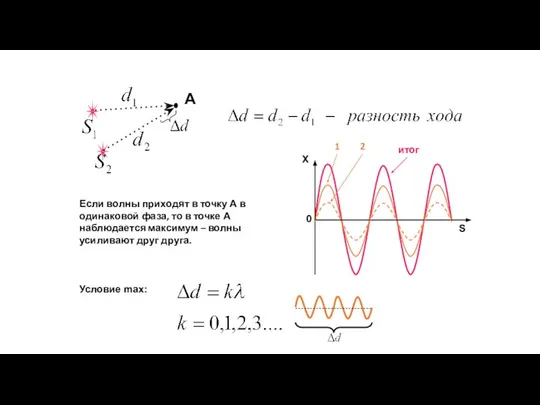
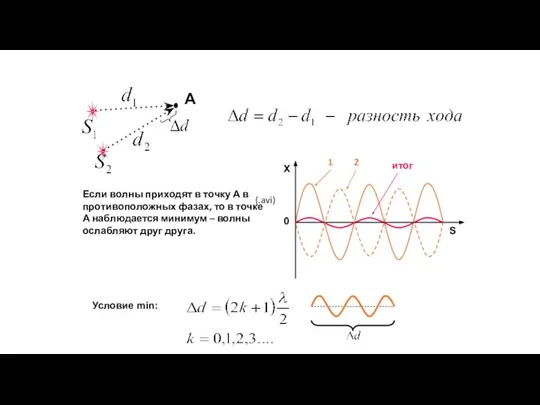
Волновая оптика
Интерференция света
Интерференция – явление сложения волн в пространстве.
От латинских слов inter – взаимно, между собой и ferio – ударяю, поражаю.
Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянна.
Источники, удовлетворяющие этим условиям, называются когерентными. (От латинского слова cohaereus – взаимосвязанный).

Если волны приходят в точку А в одинаковой фаза, то в точке А наблюдается максимум – волны усиливают друг друга.

Если волны приходят в точку А в противоположных фазах, то в точке А наблюдается минимум – волны ослабляют друг друга.
(.avi)

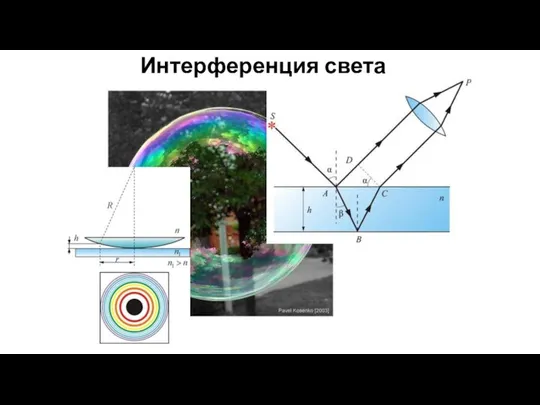
Интерференция света

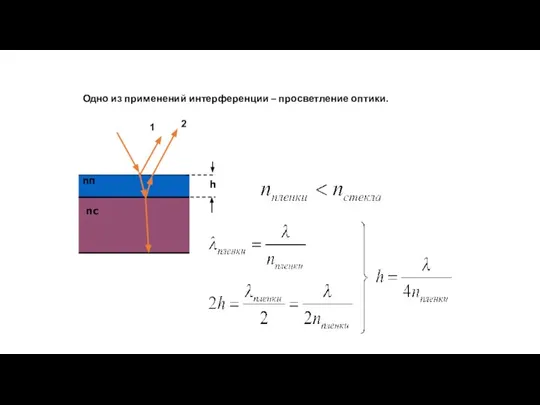
Одно из применений интерференции – просветление оптики.

Дифракция
Дифракция – явление огибания волной препятствия.
От латинского слова difraktus – разломанный.

Дифракция
Дифракция – результат интерференции вторичных волн.

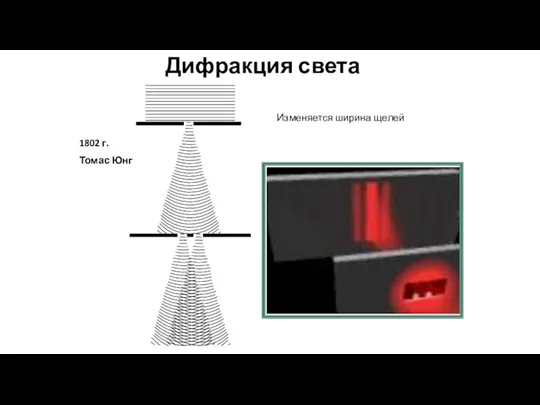
Дифракция света
1802 г.
Томас Юнг
Изменяется ширина щелей

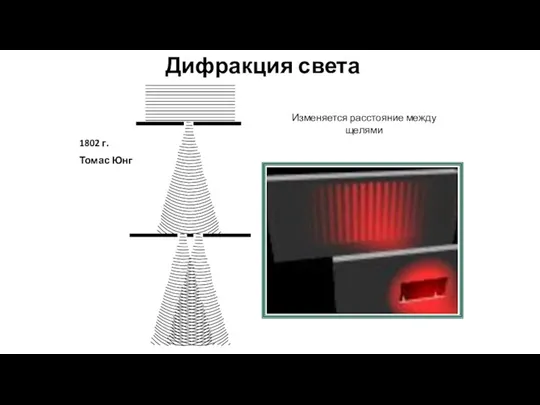
Дифракция света
1802 г.
Томас Юнг
Изменяется расстояние между щелями

Дифракция света
Принцип Гюйгенса – Френеля: волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.

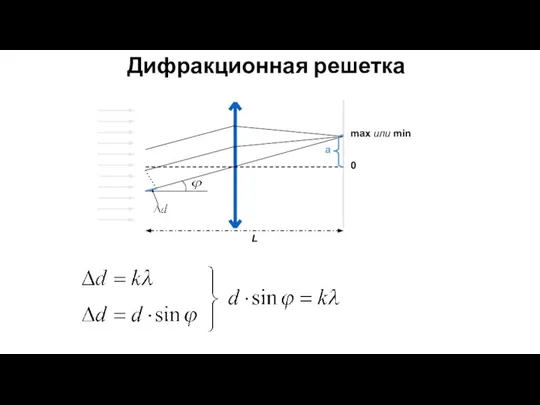
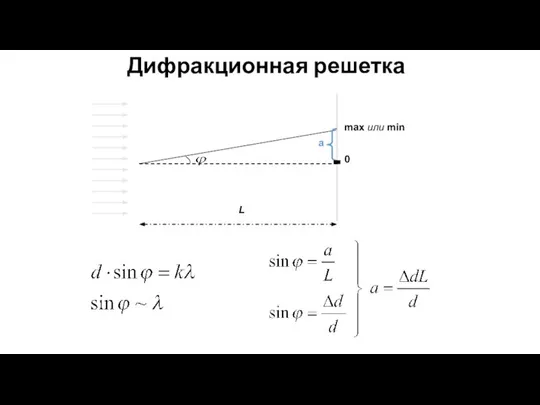
Дифракционная решетка
Дифракционная решетка представляет собой совокупность большого числа узких щелей, разделенных непрозрачными промежутками.
d – период (постоянная) дифракционной решетки.
N – число штрихов на 1 м.
d1
d2
d1>d2

Дифракционная решетка
max или min
0
a
L

Дифракционная решетка
max или min
0
a
L

Дифракционная решетка
главный max

Дифракционная решетка
главный max
1 min
1 max
1 max
2 max
2 max
3 max
3 max
1 min
2 min
2 min
3 min
3 min

Дифракционная решетка
Максимальный порядок спектра.

Дифракционная решетка
Дифракционная картина от дифракционной решетки:
Дифракционная картина от двух щелей:

Поляризация света
Свет – электромагнитная волна – поперечная волна.

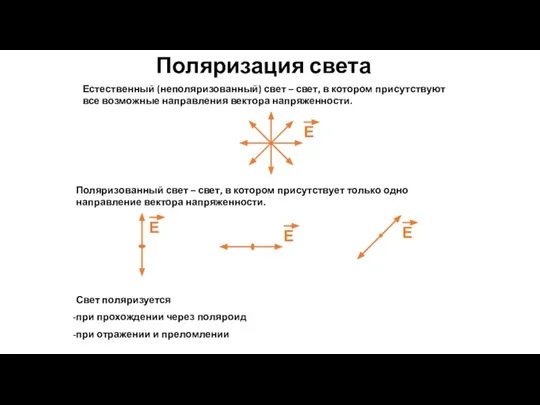
Поляризация света
Естественный (неполяризованный) свет – свет, в котором присутствуют все возможные направления вектора напряженности.
Поляризованный свет – свет, в котором присутствует только одно направление вектора напряженности.
Свет поляризуется
при прохождении через поляроид
при отражении и преломлении

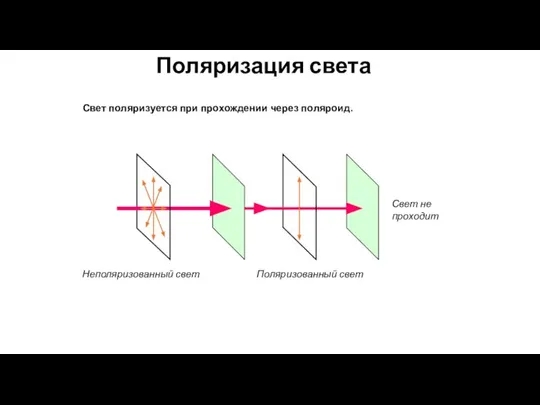
Поляризация света
Свет поляризуется при прохождении через поляроид.
Неполяризованный свет
Поляризованный свет

Поляризация света
Поляроид – вещество, вызывающее поляризацию света.

Поляризация света
При отражении и преломлении свет поляризуется.
Частичная поляризация
Полная поляризация

Основы квантовой оптики
Квантовая гипотеза Планка привела в дальнейшем к представлению о том, что свет испускается и поглощается отдельными порциями – квантами, и нашла своё подтверждение и дальнейшее развитие в ряде явлений:
Фотоэлектрический эффект фотоэффект)
Химическое действие света
Давление света
Эффект Комптона

Внешний фотоэффект
Явление было открыто Герцем в 1887 году: он заметил, что проскакивание искры между шариками разрядника облегчается, если один из шариков осветить ультрафиолетовыми лучами.
Генрих Рудольф Герц (1857-1894), немецкий физик

Внешний фотоэффект
Фотоэлектрическим эффектом или фотоэффектом называется явление вырывания электронов из твердых и жидких веществ под действием света.
Освобожденные светом электроны называются фотоэлектронами

Внешний фотоэффект
Явление зависит не только от химического состава металла, но и от состояния его поверхности, поэтому для изучения фотоэффекта используют вакуумную трубку.

Вольтамперная характеристика фотоэффекта
Кривая зависимости фототока I
от напряжения U между
электродами называется
вольтамперной характеристикой
фотоэффекта.
На рисунке: Ф – световой поток
- ток насыщения – все электроны, вылетающие из катода, попадают на анод
- задерживающее напряжение (задерживающий потенциал) – напряжение, при котором сила тока равна нулю, т.е. ни один электрон не достигает анода

Связь максимальной скорости фотоэлектронов с задерживающим потенциалом
Запишем теорему о кинетической энергии ,
где - работа задерживающего поля, а
- изменение кинетической энергии фотоэлектрона
Тогда
Отсюда получаем

Законы фотоэффекта
Закон Столетова:
Фототок насыщения прямо пропорционален падающему световому потоку
Александр Григорьевич Столетов (1839 - 1896) российский физик

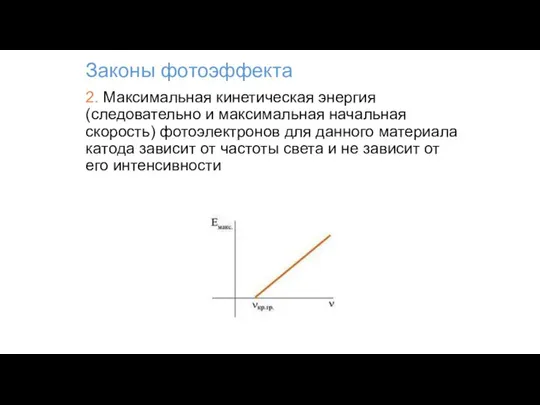
Законы фотоэффекта
2. Максимальная кинетическая энергия (следовательно и максимальная начальная скорость) фотоэлектронов для данного материала катода зависит от частоты света и не зависит от его интенсивности

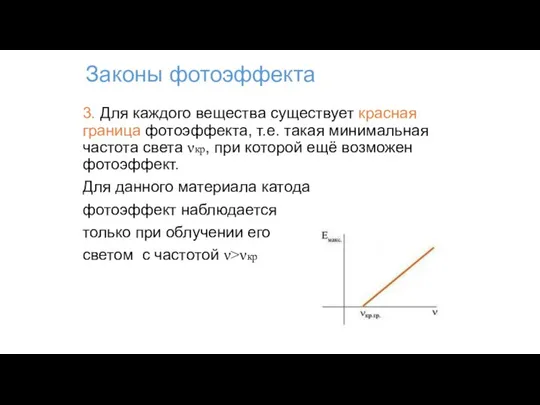
Законы фотоэффекта
3. Для каждого вещества существует красная граница фотоэффекта, т.е. такая минимальная частота света νкр, при которой ещё возможен фотоэффект.
Для данного материала катода
фотоэффект наблюдается
только при облучении его
светом с частотой ν>νкр

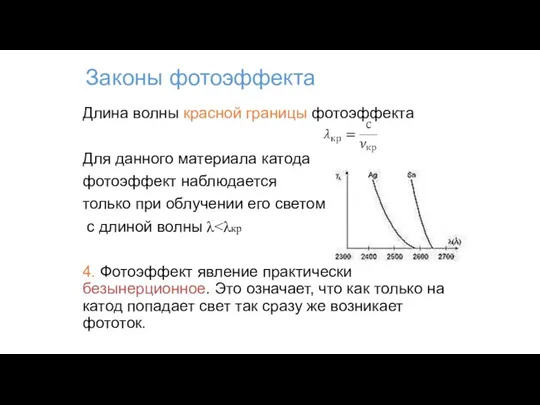
Законы фотоэффекта
Длина волны красной границы фотоэффекта
Для данного материала катода
фотоэффект наблюдается
только при облучении его светом
с длиной волны λ<λкр
4. Фотоэффект явление практически безынерционное. Это означает, что как только на катод попадает свет так сразу же возникает фототок.

Красная граница фотоэффекта

Квантовая теория внешнего фотоэффекта
С точки зрения волновой теории фотоэффект оказался необъясним. Возникшие трудности в истолковании законов фотоэффекта вызвали сомнения в универсальной применимости волновой теории света.
Квантовая гипотеза Планка позволила в 1905 г. А. Эйнштейну построить квантовую теорию фотоэффекта, за что в 1921 году он получил нобелевскую премию.

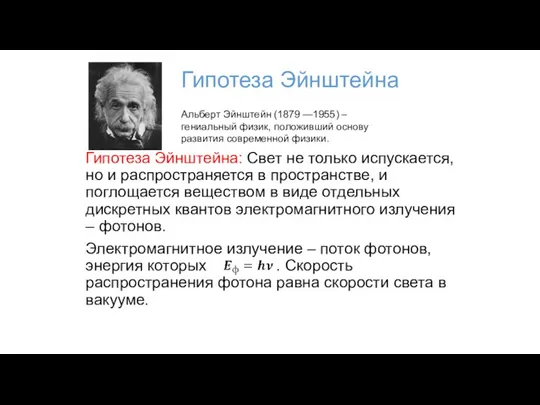
Гипотеза Эйнштейна
Гипотеза Эйнштейна: Свет не только испускается, но и распространяется в пространстве, и поглощается веществом в виде отдельных дискретных квантов электромагнитного излучения – фотонов.
Электромагнитное излучение – поток фотонов, энергия которых . Скорость распространения фотона равна скорости света в вакууме.
Альберт Эйнштейн (1879 —1955) – гениальный физик, положивший основу развития современной физики.

Уравнение Эйнштейна для фотоэффекта
Энергия падающего на катод фотона расходуется на работу выхода электрона из металла и на сообщение вылетевшему электрону кинетической энергии. По закону сохранения энергии получаем:
или или
Это уравнение называется уравнением Эйнштейна для внешнего фотоэффекта.

Уравнение Эйнштейна и его квантовая теория
позволяют объяснить 1-ый закон фотоэффекта:
Каждый квант поглощается только одним электроном, поэтому число вырванных фотоэлектронов пропорционально числу поглощенных фотонов, т.е. пропорционально интенсивности падающего света.

Уравнение Эйнштейна и его квантовая теория
позволяют объяснить 2-ой закон фотоэффекта:
При некоторой достаточно малой частоте кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится, т.е.
Красная граница фотоэффекта зависит только от работы выхода электрона из металла, т.е. от химической природы вещества и от состояния его поверхности.

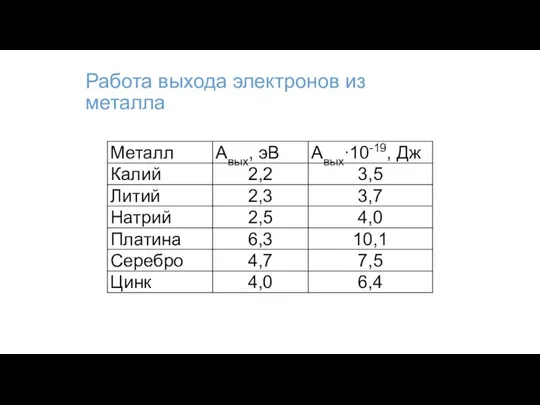
Работа выхода электронов из металла

Уравнение Эйнштейна и его квантовая теория
позволяют объяснить 3-ий закон фотоэффекта:
Максимальная кинетическая энергия фотоэлектронов для данного материала катода зависит от частоты света и не зависит от его интенсивности

Уравнение Эйнштейна и его квантовая теория
позволяют объяснить 4-ый закон фотоэффекта:
Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно.

Многофотонный фотоэффект
Когда электрон получает энергию от одного лишь фотона, то такие процессы называются однофотонными.
При очень большой интенсивности света наблюдается многофотонный фотоэффект, в ходе которого электрон, вылетающий из металла, получает энергию от N фотонов (N=2, 3, 4, 5). Формула Эйнштейна для многофотонного фотоэффекта принимает вид:

Экспериментальная проверка
квантовой теории Эйнштейна
В 1916 году Милликен создал прибор, с помощью которого измерил работу выхода, исследовал зависимость от частоты света, с высокой точностью измерил заряд электрона, экспериментально проверил квантовую теорию фотоэффекта и определил численное значение постоянной Планка.
Роберт Эндрюс Милликен (1868 — 1953) — американский физик, лауреат нобелевской премии.

Экспериментальная проверка
квантовой теории Эйнштейна
Из формул следует , что запирающее напряжение является линейной функцией частоты падающего света. Точка пересечения прямой с осью абсцисс даёт значение граничной частоты. Отсюда можно найти работу выхода
Тангенс угла наклона прямой
позволяет определить
постоянную Планка

Экспериментальная проверка
квантовой теории Эйнштейна
Дальнейшее усовершенствование методики исследования фотоэффекта было осуществлено в 1928 году П.И. Лукирским и С.С. Прилежаевым.
Лукирский Петр Иванович (1894 — 1954), советский физик.
Прилежаев Сергей Сергеевич (1903 — 1979), советский физик.

Фотоэлектрические явления и их применения
Фотоэлектрические явления нашли широкое применение в технике:
Звуковое кино
Телевидение
Видение в темноте

Виды фотоэффекта
В зависимости от судьбы электронов, поглотивших фотон, различают три основных вида фотоэффекта:
В металлах – внешний фотоэффект
В диэлектриках и полупроводниках – внутренний фотоэффект
На границе металл – полупроводник или в области p-n перехода вентильный фотоэффект

Фотоэлементы
Приборы, в которых используется фотоэффект для превращения энергии излучения в электрическую, называются фотоэлементами.
Фотоэлементы бывают разных типов:
Вакуумные фотоэлементы
Газонаполненные фотоэлементы
Фотоэлектронные умножители
Фотосопротивления (фоторезисторы)

Масса фотона
Энергия фотона
Из формулы взаимосвязи массы и энергии в СТО получаем
Отсюда масса фотона
Фотон не обладает массой покоя , т.е. покоящихся фотонов не существует

Импульс фотона
Импульс фотона и его энергия связаны соотношением
Т.к. , то
Т. к. , то импульс фотона равен
или
Если ввести волновое число , то
Направление импульса совпадает с направлением распространения света

Давление света

Давление света
В 1900 году Лебедев открыл и измерил давление света на твердые тела.
Лебедев Петр Николаевич (1866-1912), российский физик, создатель первой русской научной школы физиков

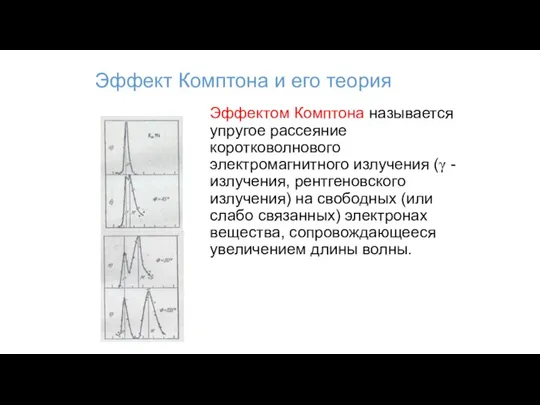
Эффект Комптона и его теория
В 1923 году Комптон, исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны λ содержатся также лучи большей длины волны λ'. Разность
оказалась зависит только от угла и не зависит от длины волны λ и от природы рассеивающего вещества.
Комптон Артур Холли
(1892—1962), американский физик

Эффект Комптона и его теория
Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (γ - излучения, рентгеновского излучения) на свободных (или слабо связанных) электронах вещества, сопровождающееся увеличением длины волны.

Эффект Комптона и его теория
Эффект Комптона объясняется на основе квантовых представлений:
это процесс упругого столкновения фотона, обладающего импульсом и энергией , с покоящимся свободным электроном (энергия покоя ), при котором фотон передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается).
Уменьшение энергии фотона и означает увеличение длины волны рассеянного излучения.

Эффект Комптона и его теория
Пусть импульс и энергия рассеянного фотона равны и
Электрон, ранее покоившийся, приобретает импульс и энергию
При этом выполняются законы сохранения энергии и импульса в системе вещество-излучение, которую можно считать изолированной.
Закон сохранения энергии
Закон сохранения импульса

Эффект Комптона и его теория
Согласно рисунку или
( (1)
Запишем закон сохранения
энергии в виде
Разделим левую и правую часть на с, получим
Возведём левую и правую части в квадрат
Сделаем замену из
получим

Эффект Комптона и его теория
Последнее выражение вычитаем из выражения (1)
(2)
(1)
Получаем или
Вместо подставляем
В результате
Учитывая, что и получаем
или

Эффект Комптона и его теория
Изменение длины волны фотона (формула Комптона)
, где
- длина волны первичного монохроматического излучения,
- длина волны рассеянного под углом ϑ к первоначальному направлению излучения.

Эффект Комптона и его теория
Из формулы следует в согласии с опытом, что увеличение длины волны при эффекте Комптона зависит только от угла рассеяния ϑ.
Величину называют комптоновской длиной волны, комптоновская длина волны для электрона равна

Эффект Комптона и его теория
Электрон, который в эффекте Комптона приобретает импульс и энергию Е называется электроном отдачи.
Кинетическая энергия электрона отдачи, как это следует из закона сохранения энергии, равна разности между энергией падающего фотона и энергией рассеянного фотона
Наибольшую кинетическую энергию электрон отдачи приобретает при

Эффект Комптона и его теория
Если электрон сильно связан с атомом, то фотон обменивается энергией и импульсом с атомом в целом, а т.к. масса атома значительно больше массы электрона, то атому передается ничтожная часть энергии фотона, т.е. в этом случае и практически не отличаются.

Эффект Комптона и его теория
Эффект Комптона наблюдается не только на электронах, но и на других частицах, например, протонах, однако, т.к. масса протона большая, то эффект просматривается только при рассеянии фотонов очень высоких энергий.

Корпускулярно-волновая двойственность света
При изучении оптических явлений физики пришли к выводу, что свет представляет собой процесс распространения электромагнитных волн. Т.к. именно волновыми свойствами объясняются такие явления как
Интерференция света
Дифракция света
Дисперсия света

Корпускулярно-волновая двойственность света
С другой стороны были обнаружены явления, которые можно объяснить, лишь исходя из представлений о свете, как о потоке частиц. Это такие явления как
Тепловое излучение
Фотоэффект
Давление света
Эффект Комптона

Корпускулярно-волновая двойственность света
Развитие теории о световых квантах привело к тому, что были установлены понятия массы и импульса фотона. Для импульса фотона справедливы соотношения
которые указывают на связь волновых характеристик света (λ, ν) с величинами (m, p), являющимися характеристиками частицы. В этом и выражается дуализм, двойственность света.

Элементы атомной и ядерной физики
Закономерности в атомных спектрах. Опыт по рассеянию альфа частиц.
Модель атома Резерфорда. Постулаты Бора.
Элементарная боровская теория водородоподобного атома.
Еще в начале XIX века были открыты дискретные спектральные линии в излучении атома водорода в видимой области (так называемый линейчатый спектр).
Впоследствии закономерности, которым подчиняются длины волн (или частоты) линейчатого спектра, были хорошо изучены количественно (И. Бальмер, 1885 г.). Совокупность спектральных линий атома водорода в видимой части спектра была названа серией Бальмера. Позже аналогичные серии спектральных линий были обнаружены в ультрафиолетовой и инфракрасной частях спектра. В 1890 году И. Ридберг получил эмпирическую формулу для частот спектральных линий:

Для серии Бальмера m = 2, n = 3, 4, 5, ... . Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, ... . Постоянная R в этой формуле называется постоянной Ридберга. Ее численное значение
R = 3,29·1015 Гц.

Первая попытка создания модели атома на основе накопленных экспериментальных данных принадлежит Дж. Томсону (1903 г.). Он считал, что атом представляет собой электронейтральную систему шарообразной формы радиусом примерно равным 10–10 м. Положительный заряд атома равномерно распределен по всему объему шара, а отрицательно заряженные электроны находятся внутри него. Для объяснения линейчатых спектров испускания атомов Томсон пытался определить расположение электронов в атоме и рассчитать частоты их колебаний около положений равновесия.

Первые прямые эксперименты по исследованию внутренней структуры атомов были выполнены Э. Резерфордом и его сотрудниками Э. Марсденом и Х. Гейгером в 1909–1911 годах. Резерфорд предложил применить зондирование атома с помощью α-частиц, которые возникают при радиоактивном распаде радия и некоторых других элементов. Масса α-частиц приблизительно в 7300 раз больше массы электрона, а положительный заряд равен удвоенному элементарному заряду. В своих опытах Резерфорд использовал α-частицы с кинетической энергией около 5 МэВ (скорость таких частиц очень велика – порядка 107 м/с, но она все же значительно меньше скорости света). α-частицы – это полностью ионизированные атомы гелия.

Опыты Резерфорда и его сотрудников привели к выводу, что в центре атома находится плотное положительно заряженное ядро, диаметр которого не превышает 10–14–10–15 м. Это ядро занимает только 10–12 часть полного объема атома, но содержит весь положительный заряд и не менее 99,95 % его массы. Веществу, составляющему ядро атома, следовало приписать плотность порядка ρ ≈ 1015 г/см3. Заряд ядра должен быть равен суммарному заряду всех электронов, входящих в состав атома. Опираясь на классические представления о движении микрочастиц, Резерфорд предложил планетарную модель атома. Разработал классическую теорию рассеяния α-частиц, и получил формулу для распределения рассеянных частиц по значению угла отклонения от первоначального направления:
Согласно планетарной модели, в центре атома располагается положительно заряженное ядро, в котором сосредоточена почти вся масса атома. Атом в целом нейтрален. Вокруг ядра, подобно планетам, вращаются под действием кулоновских сил со стороны ядра электроны.

По законам классической электродинамики, движущийся с ускорением заряд должен излучать электромагнитные волны, уносящие энергию. За короткое время (порядка 10–8 с) все электроны в атоме Резерфорда должны растратить всю свою энергию и упасть на ядро. То, что этого не происходит в устойчивых состояниях атома, показывает, что внутренние процессы в атоме не подчиняются классическим законам.
Следующий шаг в развитии представлений об устройстве атома сделал в 1913 году датский физик Н. Бор.
Первый постулат Бора (постулат стационарных состояний) гласит: атомная система может находится только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия En. В стационарных состояниях атом не излучает.

Второй постулат Бора (правило частот) формулируется следующим образом: при переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний:
где h – постоянная Планка
h=6.626 10-34 Дж с
Третий постулат (Правило квантования). Бор предположил, что из всех возможных орбит электрона осуществляются только те для которых момент импульса равен целому кратному постоянной планка h, деленной на 2π:
Число n – называется главным квантовым числом.

Применим полуклассический подход Бора к описанию движения электрона в поле ядра с зарядом Ze. При Z=1 такая система соответствует атому водорода. Произведение массы электрона на его центростремительное ускорение должно равняться силе кулона, действующей на электрон:
Видно, что радиус может принимать только дискретные значения. Внутренняя энергия атома складывается из энергии взаимодействия электрона с ядром и кинетической электрона:

Кинетическую энергию находим следующим образом:
Тогда внутренняя энергия атома
Окончательно, получим:
При переходе атома водорода (Z=1) из состояния n в состояние m излучается квант
Частота испущенного свет равна:

Элементы квантовой механики
Гипотеза де Бройля. Принцип неопределенности.
Уравнение Шредингера. Пси-функция. Ее свойства. В 1923 году французский физик Л. де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами. Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ.
Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:
Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу,

Первое экспериментальное подтверждение гипотезы де Бройля было получено в 1927 году американскими физиками К. Девиссоном и Л. Джермером. Они обнаружили, что пучок электронов, рассеивающийся на кристалле никеля, дает отчетливую дифракционную картину, подобную той, которая возникает при рассеянии на кристалле коротковолнового рентгеновского излучения. В этих экспериментах кристалл играл роль естественной дифракционной решетки. По положению дифракционных максимумов была определена длина волны электронного пучка, которая оказалась в полном соответствии с формулой де Бройля.

В следующем 1928 году английский физик Дж. Томсон получил новое подтверждение гипотезы де Бройля. В своих экспериментах Томсон наблюдал дифракционную картину, возникающую при прохождении пучка электронов через тонкую поликристаллическую фольгу из золота. На установленной за фольгой фотопластинке отчетливо наблюдались концентрические светлые и темные кольца, радиусы которых изменялись с изменением скорости электронов (т. е. длины волны) согласно де Бройлю.

В последующие годы опыт Дж. Томсона был многократно повторен с неизменным результатом, в том числе при условиях, когда поток электронов был настолько слабым, что через прибор единовременно могла проходить только одна частица (В. А. Фабрикант, 1948 г.). Таким образом, было экспериментально доказано, что волновые свойства присущи не только большой совокупности электронов, но и каждому электрону в отдельности.

Новая теория, которая учитывает корпускулярно-волновой дуализм микрочастиц, называется волновая или квантовая механика. Основным уравнением квантовой механики является уравнение Шредингера. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем обстоятельством, что все вытекающие из него следствия точным образом согласуются с опытными фактами.
Состояние микрочастицы описывается в квантовой механике волновой функцией Ψ. Она является функцией координат и времени и может быть найдена путем решения уравнения:
Это уравнение было установлено Шредингером в 1926 г. И называется уравнением Шредингера со временем.
В это уравнение входят следующие величины: i – мнимая единица, m – масса частицы, - оператор Лапласа

U – потенциальная энергия частицы.
Как следует из уравнения Шредингера, волновая функция определяется потенциальной энергией, т.е. видом сил действующих на частицу. Если потенциальная энергия остается постоянной во времени, то волновая функция распадается на два множителя, один из которых зависит только от времени, второй только от координат.
где Е – полная энергия частицы. Для случая стационарного поля уравнение Шредингера преобразуется к следующему виду.
Это соотношение называется уравнением Шредингера для стационарных состояний.

Физический смысл Ψ функции состоит в следующем: квадрат модуля Ψ определяет вероятность dP того, что частица будет обнаружена в пределах объема dV:
Волновые функции должны всегда быть нормированы таким образом, чтобы:
Волновые функции, получаемые из решений уравнения Шредингера должны удовлетворять следующим условиям:
1) однозначность;
2) конечность;
3) непрерывность.
Эти условия должны выполняться во всей области изменения переменных x, y, z. Они являются следствием того факта, что волновая функция по своему физическому смыслу определяет вероятность.

Уровни энергии, волновые функции, распределение плотности вероятности по координате х

При определенных условиях понятия положения в пространстве и траектории оказываются приближенно применимыми к движению микрочастиц. Степень точности, с какой к частице может быть применено представление об определенном положении ее в пространстве, дается соотношением неопределенностей, установленным Гейзенбергом. Наиболее важным являются два соотношения неопределенностей.
Первое из них ограничивает точности одновременного измерения координат и соответствующих проекций импульса частицы. Для проекции, например на ось Х оно выглядит следующим образом:
Второе соотношение устанавливает неопределенность измерения энергии, ΔЕ, за данный промежуток времени Δt:

Квантовые числа.
ГЛАВНОЕ КВАНТОВОЕ ЧИСЛО (n)
Решая уравнение Шрединегера на движение электронов в атоме, можно получить, что волновая функция электронов определяется набором четырех квантовых чисел.
Число (n) характеризует общую энергию электрона в атоме. Оно может принимать значения целых чисел:
1, 2, 3 … n
Каждому значению квантового числа n соответствует свой энергетический уровень.
Число энергетических уровней в атоме заселенных электронами, равно номеру периода, в котором находится элемент в таблице Менделеева.

ГЛАВНОЕ КВАНТОВОЕ ЧИСЛО (n)
Например – электроны в атоме любого элемента, принадлежащего третьему периоду, располагаются на трех энергетических уровнях.
Электроны, находящиеся на ближайшем к ряду энергетическом уровне (n=1) обладают наименьшей энергией. При поглощении квантовой энергии (Е=hν) электрон переходит на более высокий энергетический уровень. При переходе на более низкий уровень – электрон испускает квант энергию.

ОРБИТАЛЬНОЕ КВАНТОВОЕ ЧИСЛО (ɭ )
Число ɭ определяет форму орбитали, а следовательно и электронного облака. Оно может принимать значение от нуля до n-1:
ɭ = 0, 1, 2, 3 … n-1
Например, если главное квантовое число равно четырем (n=4), то ɭ принимает значения 0, 1, 2, 3.

Электроны с одинаковыми значениями числа n, но разными ( ɭ ) , несколько отличаются по энергии. Поэтому говорят, что электроны данного энергетического уровня группируются в энергетические подуровни.
ОРБИТАЛЬНОЕ КВАНТОВОЕ ЧИСЛО (ɭ )
Этим подуровням присвоены следующие буквенные обозначения:
Орбитальное квантовое число (l) 0 1 2 3
Обозначение энергетического s p d f
подуровня
(продолжение)

Число подуровней в каждом энергетическом уровне равно его квантовому числу, т.е. номеру этого уровня.
Первый энергетический уровень (n=1) состоит из одного s – подуровня; второй (n=2) – из двух (s; p) подуровней; третий (n=3) – из трех (s; p; d) подуровней; четвертый (n=4) – из четырех (s; p; d; f) подуровней:
Главное квантовое
число (n)
(номер уровня)
1
2
3
4
Типы подуровней
s
s, p
s, p, d
s, p, d, f
ОРБИТАЛЬНОЕ КВАНТОВОЕ ЧИСЛО (ɭ )
(продолжение)

ОРБИТАЛЬНОЕ КВАНТОВОЕ ЧИСЛО (l)
И ФОРМЫ ОРБИТАЛЕЙ
Орбитали (электроны), для которых ( ɭ ) = 0, 1, 2, 3 соответственно называются s-, p-, d-, f- орбиталями (или s-, p-, d-, f- электронами). Наименьшей энергией обладают s- электроны, далее p-, d-, f- электроны.
Формы s-, p- орбиталей (электронов) представлены на рисунке.
x
x
x
z
Py
Pz
y
y
y
z
z
Px

Магнитное квантовое число
Принимает значения m = 0, ±1,±2, ± l
Определяет проекцию момента импульса электрона на заданное направление
Пространственное квантование:
Таким образом
принимает
2l + 1 ориентаций в пространстве

СВЯЗЬ МАГНИТНОГО И ОРБИТАЛЬНОГО
КВАНТОВЫХ ЧИСЕЛ
Орбитальное
квантовое число
( ɭ )
Магнитное
квантовое
число (m)
Число орбиталей
(облаков)
0
1
2
3
0
– 1, 0, + 1
– 2, – 1, 0, + 1, + 2
–3, – 2, – 1, 0,
+ 1, + 2, + 3
1
3
5
7

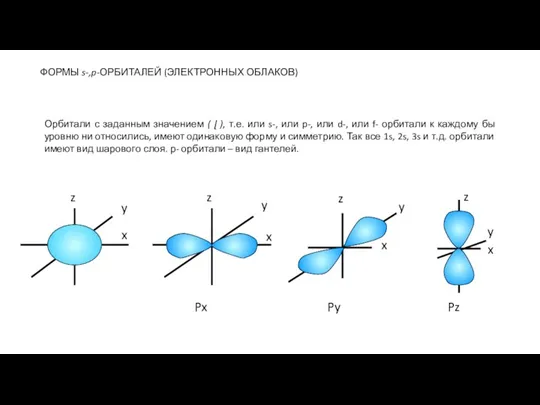
ФОРМЫ s-,p-ОРБИТАЛЕЙ (ЭЛЕКТРОННЫХ ОБЛАКОВ)
Орбитали с заданным значением ( ɭ ), т.е. или s-, или p-, или d-, или f- орбитали к каждому бы уровню ни относились, имеют одинаковую форму и симметрию. Так все 1s, 2s, 3s и т.д. орбитали имеют вид шарового слоя. р- орбитали – вид гантелей.

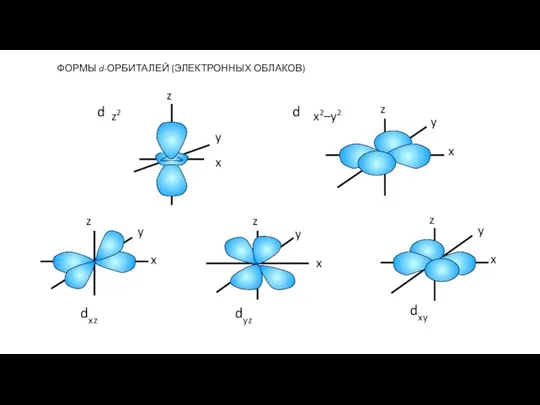
z2
x2–y2
dxy
x
y
z
x
y
z
x
y
z
x
y
z
x
y
z
d
d
dxz
dyz
ФОРМЫ d-ОРБИТАЛЕЙ (ЭЛЕКТРОННЫХ ОБЛАКОВ)

СПИНОВОЕ КВАНТОВОЕ ЧИСЛО (S)
При данном значении m, число s может иметь всего два значения:
Гипотеза о наличии у электрона так называемого спина была выдвинута в 1925 г. (сначала - для наглядности - считалось, что это явление аналогично вращению земли вокруг своей оси при движении ее по орбите вокруг Солнца).
+ ½ и – ½
На самом деле, спин - это чисто квантовое свойство электрона, не имеющее классических аналогов. Строго говоря, спин - это собственный момент импульса электрона, не связанный с движением в пространстве.
Для всех электронов абсолютное значение спина всегда равно s = 1/2. Проекция спина на ось Z (магнитное спиновое число) может иметь лишь два значения: mS= +1/2 или mS = -1/2.

«В атоме не может быть двух электронов с одинаковыми значениями всех четырех квантовых чисел».
Так как АО характеризуется тремя квантовыми числами n, l, m, то в ней могут находиться не более двух электронов с противоположными спинами:
ПРИНЦИП ПАУЛИ
Xe = 2 (2l + 1); s–2; p–6; d – 10; f – 14
Максимальное число электронов равно:
На подуровне:
На уровне:

«При заполнении электронами уровней и подуровней, последовательность размещения электронов в атоме должна отвечать наибольшей связи их с ядром, т.е. электрон должен обладать наименьшей энергией».
ПРИНЦИП НАИМЕНЬШЕЙ ЭНЕРГИИ
Этот принцип выражает общие термодинамические требования к устойчивости систем: максимум устойчивости соответствует минимум энергии.
«В первую очередь заполняются те подуровни, для которых сумма значений главного и побочного квантовых чисел (n + l) является наименьшей; при одинаковой сумме (n + l) сначала заполняется подуровень с меньшим значением главного квантового числа n».
Правила Клечковского

ПОСЛЕДОВАТЕЛЬНОСТЬ ЗАПОЛНЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ И ПОДУРОВНЕЙ
1s→2s→2p→3s→4s→3d→4p→5s→4d→5p→
→ 6s→/5d1/→4f→5d→6p→7s→/6d1– 2/→5f→6d

«В пределах данного энергетического подуровня электроны располагаются так, что суммарное спиновое число их /ΣS/ максимально»:
ПРАВИЛО ХУНДА
или
ΣS = ½ + ½ +½ = +3/2; ΣS = – ½ – ½ –½ = –3/2
Всякое другое распределение неверно:

В электронных формулах буквами s, p, d, f обозначаются энергетические электроны.
Цифры впереди букв означают энергетический уровень, в котором находится данный электрон, а индекс вверху справа – число электронов на данном подуровне
Запись 5p3 означает, что на p- подуровне пятого энергетического уровня располагаются три электрона.
ЭЛЕКТРОННЫЕ ФОРМУЛЫ АТОМОВ

При составлении электронной формулы атома любого элемента нужно руководствоваться следующей последовательностью:
1. Определить порядковый номер элемента (а, следовательно, число электронов в атоме);
2. Определить число энергетических уровней, на которых будут располагаться электроны /по номеру периода/;
3. Распределить электроны по подуровням и уровням, руководствуясь требованиями основных положений.
ЭЛЕКТРОННЫЕ ФОРМУЛЫ АТОМОВ

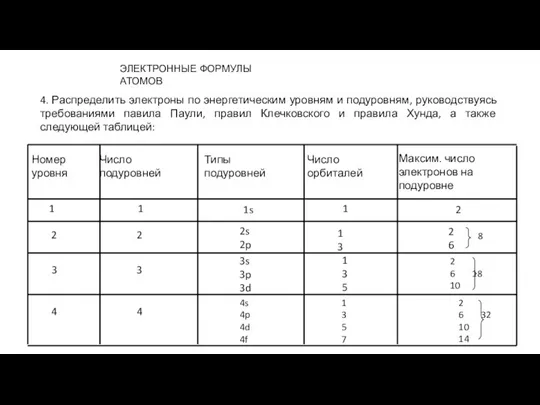
4. Распределить электроны по энергетическим уровням и подуровням, руководствуясь требованиями павила Паули, правил Клечковского и правила Хунда, а также следующей таблицей:
ЭЛЕКТРОННЫЕ ФОРМУЛЫ АТОМОВ
Номер
уровня
Число
подуровней
Типы
подуровней
Число
орбиталей
Максим. число
электронов на
подуровне
1
1
1s
1
2
2
2
2s
2p
1
3
2
6
3
3
3s
3p
3d
1
3
5
2
18
10
4
4
4s
4p
4d
4f
1
3
5
7
2
32
10
14
8

Периодическая система элементов Д.И.Менделеева
Дмитрий Иванович МЕНДЕЛЕЕВ
(8.II.1834 - 2.II.1907) - великий русский ученый-энциклопедист, химик, физик, технолог, геолог и даже метеоролог. Менделеев был членом более 90 академий наук, научных обществ, университетов разных стран. Он является одним и основателей Русского химического общества; неоднократно избирался его президентом. Имя ученого – Менделеевий – носит 101-й элемент в периодической таблице.

Теория периодической системы элементов Д.И.Менделеева
Порядковый номер химического элемента равен общему числу электронов в атоме данного элемента;
Состояние электронов в атоме определяется набором их квантовых чисел. Распределение электронов по энергетическим состояниям должно удовлетворять принципу минимума потенциальной энергии;
Заполнение электронами энергетических состояний в атоме должно происходить в соответствии с принципом Паули.

Заполнение электронных состояний
Порядковый номер химического элемента равен общему числу электронов в атоме данного элемента;
Состояние электронов в атоме определяется набором их квантовых чисел. Распределение электронов по энергетическим состояниям должно удовлетворять принципу минимума потенциальной энергии;
Заполнение электронами энергетических состояний в атоме должно происходить в соответствии с принципом Паули.

Состав и характеристики атомного ядра. Масса и энергия связи ядра. Радиоактивность. Виды радиоактивности. Альфа-распад. Бета-распад.
К 20-м годам XX века физики уже не сомневались в том, что атомные ядра, открытые Э. Резерфордом в 1911 г., также как и сами атомы, имеют сложную структуру. В этом их убеждали многочисленные экспериментальные факты, накопленные к этому
времени: открытие радиоактивности,
экспериментальное доказательство ядерной
модели ядра, измерение отношения e / m
для электрона, α-частицы и для так называемой
H-частицы – ядра атома водорода, открытие
искусственной радиоактивности и ядерных
реакций, измерение зарядов атомных ядер и т. д.
В настоящее время твердо установлено, что атомные ядра различных элементов состоят из двух частиц – протонов и нейтронов.

В ядерной физике массу частицы часто выражают в атомных единицах массы (а. е. м.), равной 1/12 массы атома углерода с массовым числом 12:
1 а.е.м.=1.66057 ·10-27 кг
mp = 1,007276 · а. е. м.
Во многих случаях массу частицы удобно выражать в эквивалентных значениях энергии в соответствии с формулой E = mc2. Так как 1 эВ = 1,60218·10–19 Дж, в энергетических единицах масса протона равна
938,272331 МэВ.
По современным измерениям, положительный заряд протона в точности равен элементарному заряду e = 1,60217733·10–19 Кл, то есть равен по модулю отрицательному заряду электрона. В настоящее время равенство зарядов протона и электрона проверено с точностью 10–22. Масса протона, по современным измерениям, равна
mp = 1,67262·10–27 кг.

Нейтрон – это нейтральная частица. По современным измерениям, масса нейтрона
mn = 1,67493·10–27 кг = 1,008665 а. е. м.
В энергетических единицах масса нейтрона равна 939,56563 МэВ. Масса нейтрона приблизительно на две электронные массы превосходит массу протона.
Для характеристики атомных ядер вводится ряд обозначений. Число протонов, входящих в состав атомного ядра, обозначают символом Z и называют зарядовым числом или атомным номером (это порядковый номер в периодической таблице Менделеева). Заряд ядра равен Ze, где e – элементарный заряд. Число нейтронов обозначают символом N.
Общее число нуклонов (т. е. протонов и нейтронов) называют массовым числом A:
A=Z+N

Ядра химических элементов обозначают символом
где X – химический символ элемента.
Энергия связи ядра равна минимальной энергии, которую необходимо затратить для полного расщепления ядра на отдельные частицы. Из закона сохранения энергии следует, что энергия связи равна той энергии, которая выделяется при образовании ядра из отдельных частиц. Энергию связи любого ядра можно определить с помощью точного измерения его массы. Эти измерения показывают, что масса любого ядра Mя всегда меньше суммы масс входящих в его состав протонов и нейтронов.
Mя < Zmp + Nmn
Разность масс
ΔM = Zmp + Nmn – Mя.
называется дефектом массы.

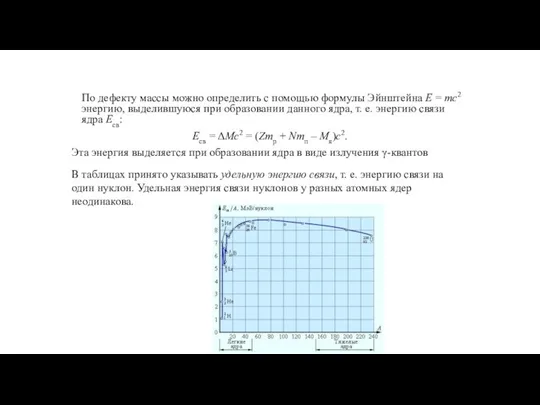
По дефекту массы можно определить с помощью формулы Эйнштейна E = mc2 энергию, выделившуюся при образовании данного ядра, т. е. энергию связи ядра Eсв:
Eсв = ΔMc2 = (Zmp + Nmn – Mя)c2.
Эта энергия выделяется при образовании ядра в виде излучения γ-квантов
В таблицах принято указывать удельную энергию связи, т. е. энергию связи на один нуклон. Удельная энергия связи нуклонов у разных атомных ядер неодинакова.

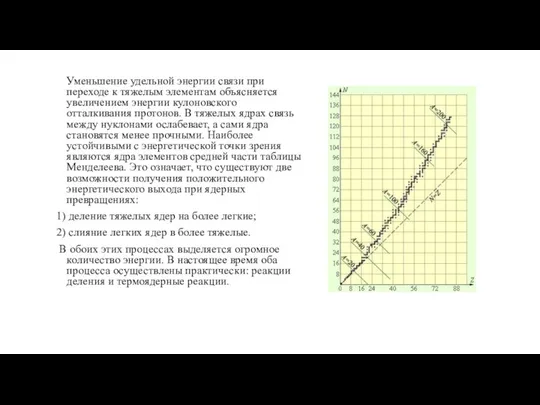
Уменьшение удельной энергии связи при переходе к тяжелым элементам объясняется увеличением энергии кулоновского отталкивания протонов. В тяжелых ядрах связь между нуклонами ослабевает, а сами ядра становятся менее прочными. Наиболее устойчивыми с энергетической точки зрения являются ядра элементов средней части таблицы Менделеева. Это означает, что существуют две возможности получения положительного энергетического выхода при ядерных превращениях:
1) деление тяжелых ядер на более легкие;
2) слияние легких ядер в более тяжелые.
В обоих этих процессах выделяется огромное количество энергии. В настоящее время оба процесса осуществлены практически: реакции деления и термоядерные реакции.

Почти 90 % из известных 2500 атомных ядер нестабильны. Нестабильное ядро самопроизвольно превращается в другие ядра с испусканием частиц. Это свойство ядер называется радиоактивностью.
Так как радиоактивный распад имеет случайный характер и не зависит от внешних условий, то закон убывания количества N(t) нераспавшихся к данному моменту времени t ядер может служить важной статистической характеристикой процесса радиоактивного распада.
N0 – число нераспавшихся частиц в начальный момент времени,
λ – постоянная радиоактивного распада, которая характеризует вероятность распада ядра в единицу времени.

За время
τ = 1 / λ
количество нераспавшихся ядер уменьшится в e ≈ 2,7 раза. Величину τ называют средним временем жизни радиоактивного ядра. Для практического использования закон радиоактивного распада удобно записать в другом виде, используя в качестве основания число 2, а не e:
Величина T называется периодом полураспада. За время T распадается половина первоначального количества радиоактивных ядер. Величины T и τ связаны соотношением

Альфа-распадом называется самопроизвольное превращение атомного ядра с числом протонов Z и нейтронов N в другое (дочернее) ядро, содержащее число протонов Z – 2 и нейтронов N – 2. При этом испускается α-частица – ядро атома гелия . Примером такого процесса может служить α-распад радия:
При бета-распаде из ядра вылетает электрон. Внутри ядер электроны существовать не могут, они возникают при β-распаде в результате превращения нейтрона в протон. Этот процесс может происходить не только внутри ядра, но и со свободными нейтронами. Среднее время жизни свободного нейтрона составляет около 15 минут. При распаде нейтрон превращается в протон и электрон . В процессе распада нейтрона возникает частица, которая называется электронным антинейтрино