Вихревая линия, вихревая поверхность, вихревая трубка, вихревой жгут, вихрь

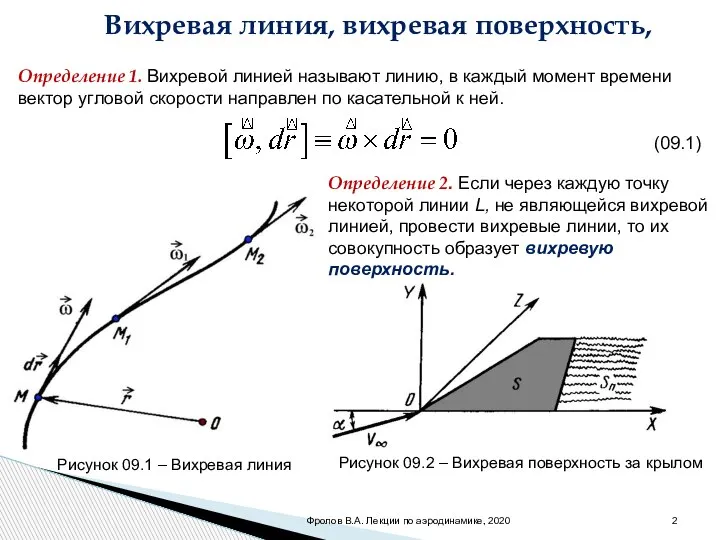
Вихревая линия, вихревая поверхность,
Определение 1. Вихревой линией называют линию, в каждый момент времени вектор угловой скорости направлен по касательной к ней.
(09.1)
Рисунок 09.1 – Вихревая линия
Определение 2. Если через каждую точку некоторой линии L, не являющейся вихревой линией, провести вихревые линии, то их совокупность образует вихревую поверхность.
Рисунок 09.2 – Вихревая поверхность за крылом
Фролов В.А. Лекции по аэродинамике, 2020

Дифференциальное уравнение вихревой линии
Фролов В.А. Лекции по аэродинамике, 2020
Условие коллинеарности двух векторов
(09.2)
(09.3)
(09.4)
Другое условие коллинеарности двух векторов

Вихревая трубка, вихревой жгут, вихрь, интенсивность вихря
Определение 3. Если линия L является замкнутым контуром, то вихревая поверхность превращается в вихревую трубку.
Определение 4. Вихревая трубка вместе с заключённым в ней вращающимся воздухом образует вихревой жгут, который обычно для краткости называют вихрем.
Определение 5. Интенсивностью или напряжением вихря J называют удвоенный поток вектора угловой скорости через поперечное сечение вихря S
(09.5)
Определение 6. Циркуляцией скорости Г по замкнутому контуру L называют криволинейный интеграл вида
(09.6)
Рисунок 9.3 – Определение циркуляции
Фролов В.А. Лекции по аэродинамике, 2020

Теорема Стокса
Теорема Стокса: циркуляция скорости по замкнутому контуру L равна суммарной интенсивности вихрей, пересекающих произвольную поверхность S, опирающийся на этот контур
Рисунок 9.4 – Вихри, пересекающие поверхность S, опирающуюся на контур L
(09.7)
Для одного вихря
(09.8)
Фролов В.А. Лекции по аэродинамике, 2020

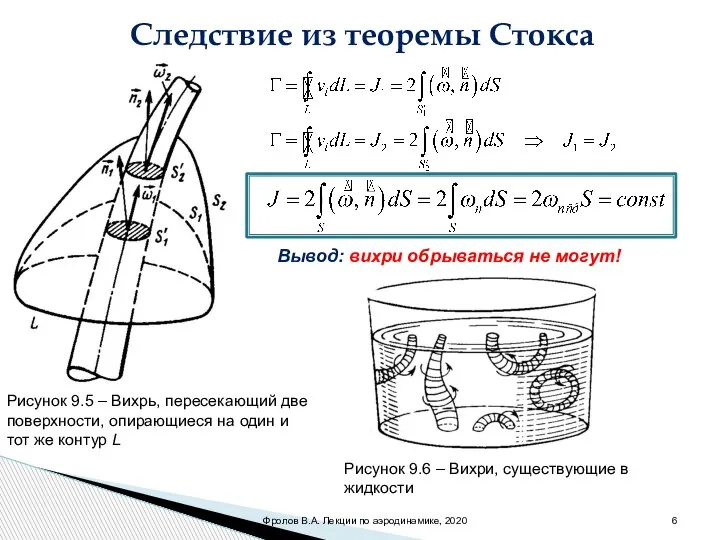
Следствие из теоремы Стокса
Рисунок 9.5 – Вихрь, пересекающий две поверхности, опирающиеся на один и тот же контур L
Вывод: вихри обрываться не могут!
Рисунок 9.6 – Вихри, существующие в жидкости
Фролов В.А. Лекции по аэродинамике, 2020

Теоремы Гельмгольца
Теорема 1. В непрерывных течениях идеального газа вихревая трубка с течением времени не разрушается и всегда остаётся вихревой трубкой.
Теорема 2. В непрерывных течениях идеального газа напряжение вихревого жгута с течением времени не изменяется.
Фролов В.А. Лекции по аэродинамике, 2020

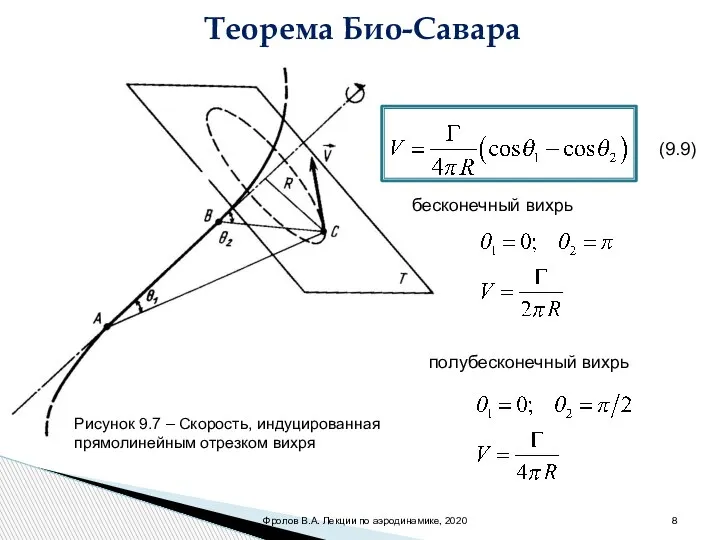
Теорема Био-Савара
Рисунок 9.7 – Скорость, индуцированная прямолинейным отрезком вихря
(9.9)
бесконечный вихрь
полубесконечный вихрь
Фролов В.А. Лекции по аэродинамике, 2020

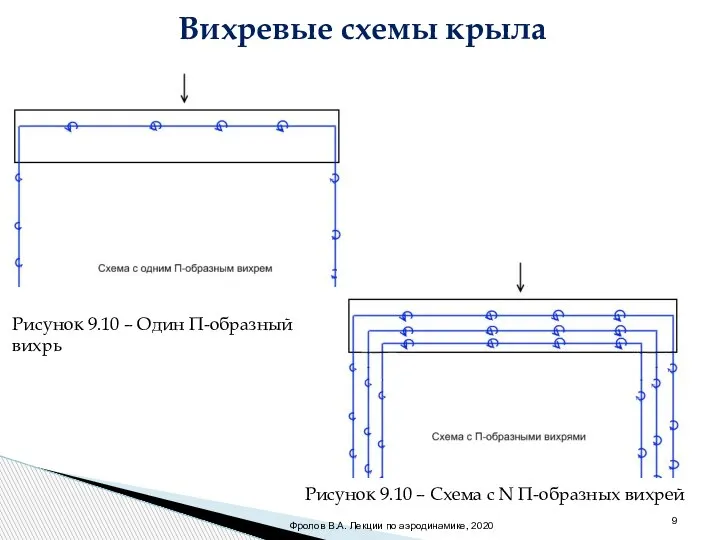
Вихревые схемы крыла
Фролов В.А. Лекции по аэродинамике, 2020
Рисунок 9.10 – Один П-образный вихрь
Рисунок 9.10 – Схема с N П-образных вихрей

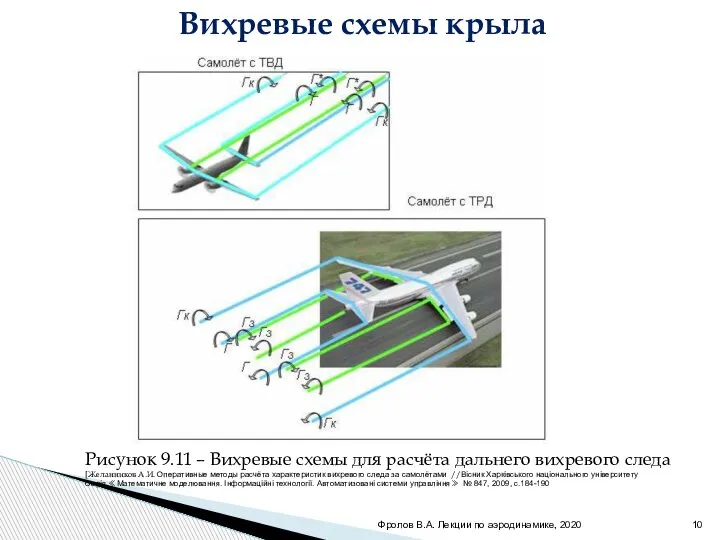
Фролов В.А. Лекции по аэродинамике, 2020
Рисунок 9.11 – Вихревые схемы для расчёта дальнего вихревого следа
[Желанников А.И. Оперативные методы расчёта характеристик вихревого следа за самолётами //Вісник Харківського національного університету
Серія ≪Математичне моделювання. Інформаційні технології. Автоматизовані системи управління≫ № 847, 2009, с.184-190
Вихревые схемы крыла

[Аэродинамика летальных аппаратов /Под ред. Колесникова Г.А., 1993, с. 391]
Фролов В.А. Лекции по аэродинамике, 2020
Рисунок 9.12 – Расчётная схема МДВ
(линейная модель)
Рисунок 9.13 – Расчётная схема МДВ (нестационарная модель)
Метод дискретных вихрей

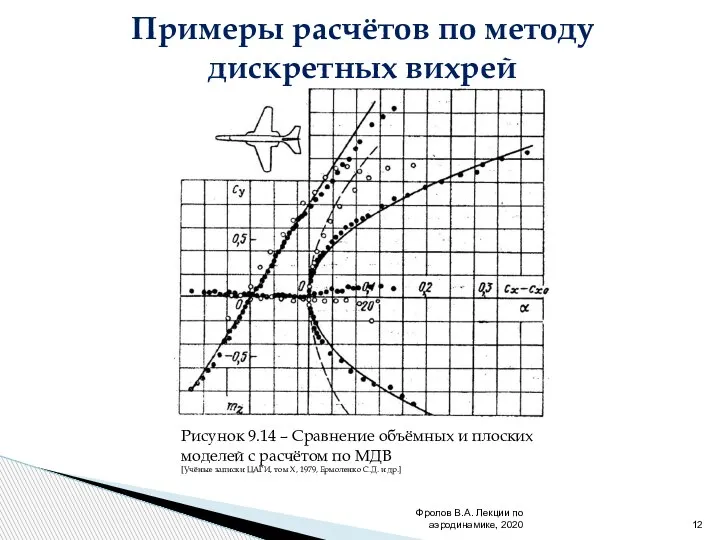
Фролов В.А. Лекции по аэродинамике, 2020
Рисунок 9.14 – Сравнение объёмных и плоских моделей с расчётом по МДВ
[Учёные записки ЦАГИ, том X, 1979, Ермоленко С.Д. и др.]
Примеры расчётов по методу дискретных вихрей

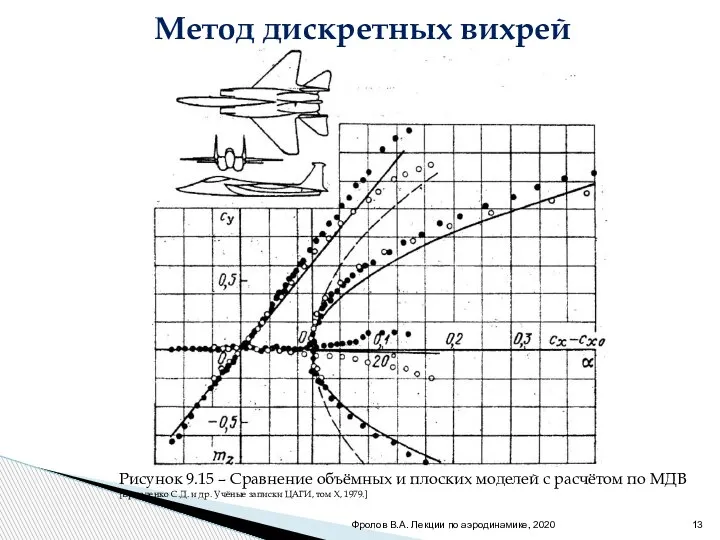
Фролов В.А. Лекции по аэродинамике, 2020
Метод дискретных вихрей
Рисунок 9.15 – Сравнение объёмных и плоских моделей с расчётом по МДВ
[Ермоленко С.Д. и др. Учёные записки ЦАГИ, том X, 1979.]

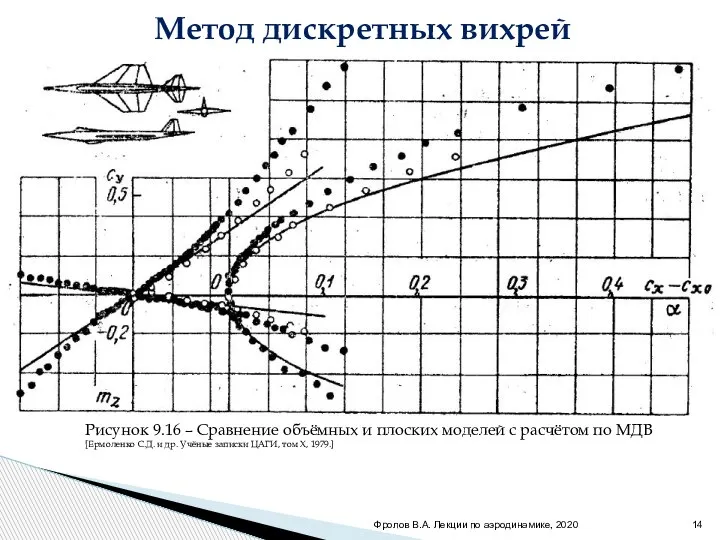
Фролов В.А. Лекции по аэродинамике, 2020
Метод дискретных вихрей
Рисунок 9.16 – Сравнение объёмных и плоских моделей с расчётом по МДВ
[Ермоленко С.Д. и др. Учёные записки ЦАГИ, том X, 1979.]