Содержание
- 2. Задачи, поставленные на второй семестр Суть нашего проекта заключается в моделировании и оптимизации траектории полетов космических
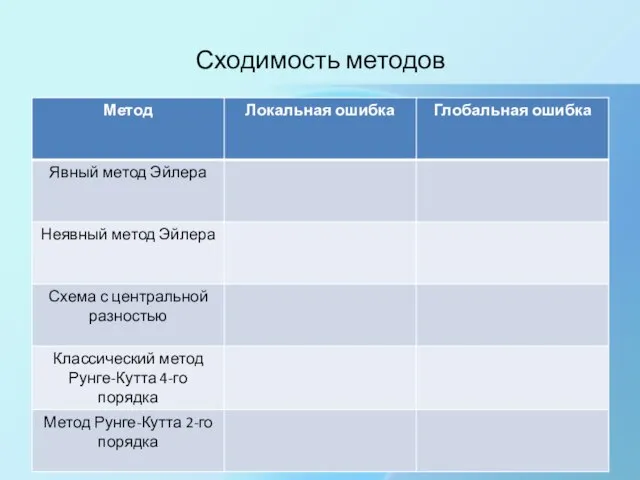
- 3. Сходимость методов
- 4. Задача Коши Рассмотрим одну из наиболее часто встречающихся задач — задачу Коши. По заданному условию находится
- 5. Задача двух тел
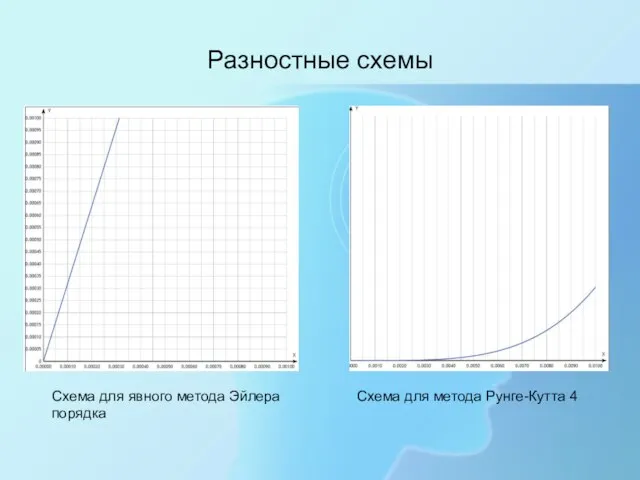
- 6. Разностные схемы Схема для явного метода Эйлера Схема для метода Рунге-Кутта 4 порядка
- 7. Список литературы [1] Федоренко Р.П., «Введение в вычислительную физику». – 1994 [2] Калиткин Н.Н., «Численные методы».
- 9. Процесс решения задачи Построение математической модели заданного физического процесса Компьютерное моделирование процесса при помощи построенной математической
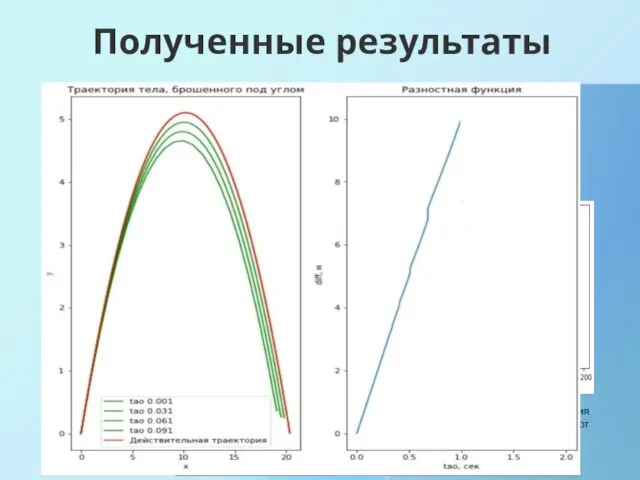
- 10. Полученные результаты При решении задачи о движении тел, брошенного под углом к горизонту, использовались такие физические
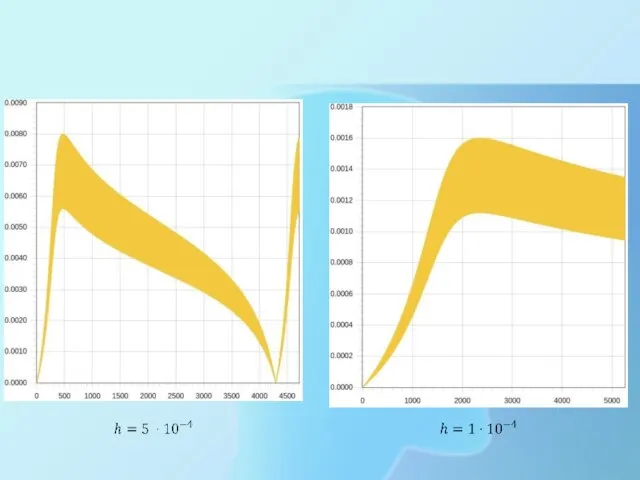
- 11. Полученные результаты Полученная численными методами траектория Зависимость максимального отклонения численного и аналитических решений от величины разбиения
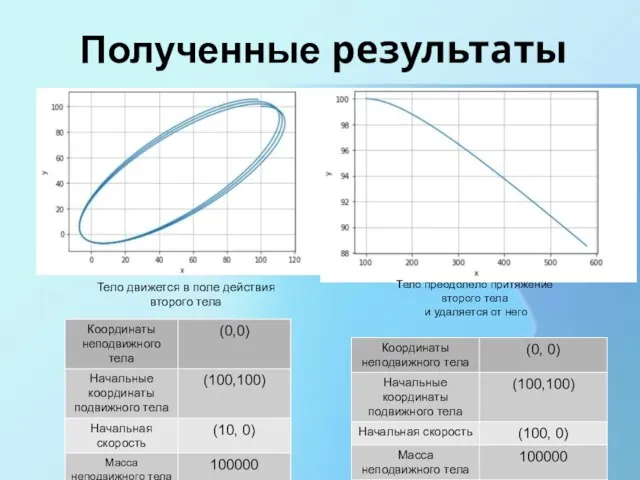
- 12. Полученные результаты Далее была решена задача, в которой рассматривается два тела, одно из которых покоится, А
- 13. Полученные результаты Тело движется в поле действия второго тела Тело преодолело притяжение второго тела и удаляется
- 14. В данный момент мы решаем, так называемую, задачу двух тел. Её формулировка следующая: даны два тела,
- 15. Задача двух тел
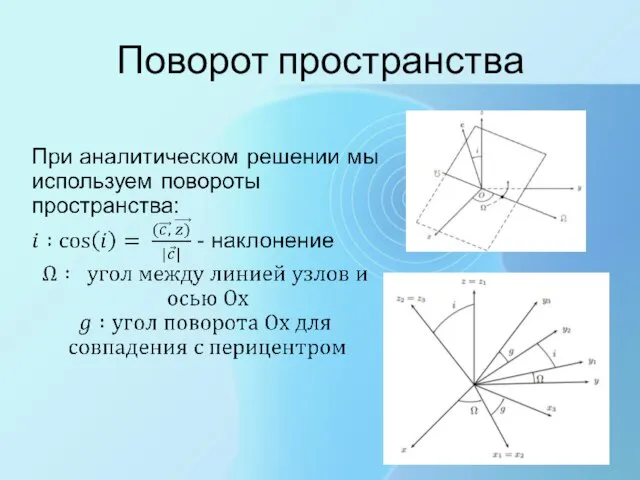
- 16. Поворот пространства
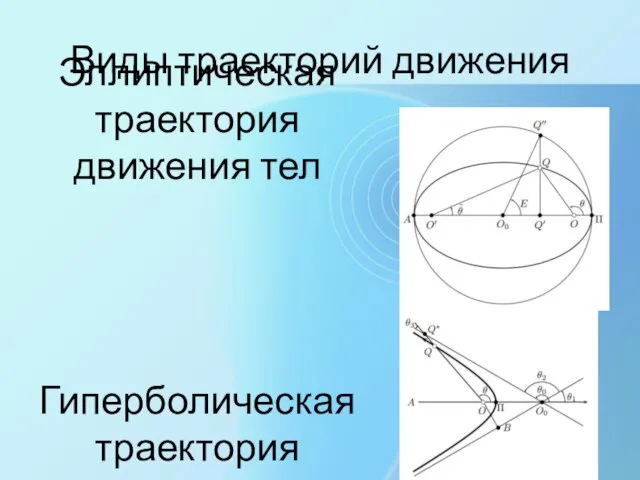
- 17. Виды траекторий движения Эллиптическая траектория движения тел Гиперболическая траектория движения тел
- 18. Имеем выражение для истинной и эксцентричной аномалии: Дифференцируем его: Переписываем полученное выражение, где n константа для
- 19. По своей сути, задача двух тел – один из случаев задачи Коши, рассмотренной ранее. Метод Рунге-Кутты
- 20. Явные методы Рунге-Кутта
- 21. Метод Рунге - Кутты с автоматическим выбором шага
- 23. Оптимизация траектории - процесс проектирования траектории, который сводит к минимуму (или максимизирует) некоторую меру производительности при
- 24. Прямой метод решения задачи оптимизации траектории состоит из двух этапов: 1) Непосредственно дискретизировать задачу оптимизации траектории,
- 25. Одиночная стрельба – ограничение дефекта на всем сегменте Многократная стрельба – ограничение дефекта на множестве сегментов
- 27. Скачать презентацию



![Список литературы [1] Федоренко Р.П., «Введение в вычислительную физику». – 1994 [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/851939/slide-6.jpg)













 Основное уравнение динамики вращательного движения твердого тела. (Лекция 7)
Основное уравнение динамики вращательного движения твердого тела. (Лекция 7) Видатні вчені фізики
Видатні вчені фізики Температура. Виды термометров
Температура. Виды термометров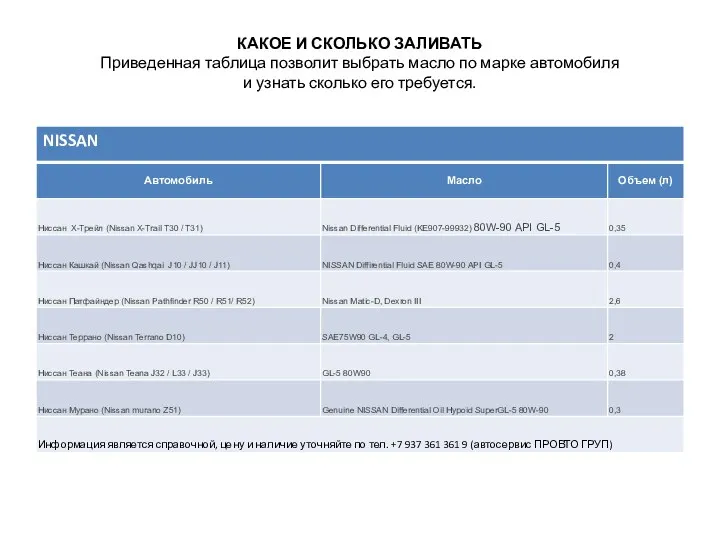 Объем заправочных масел
Объем заправочных масел Тепловые процессы: нагревание, охлаждение, конденсация и выпаривание
Тепловые процессы: нагревание, охлаждение, конденсация и выпаривание Маса. інертність
Маса. інертність Выталкивающая сила. Закон Архимеда
Выталкивающая сила. Закон Архимеда Презентация на тему Ультрафиолетовые лучи
Презентация на тему Ультрафиолетовые лучи  ВКР: Совершенствование системы ТО с разработкой приспособления для обслуживания тормозной системы
ВКР: Совершенствование системы ТО с разработкой приспособления для обслуживания тормозной системы Курс лекций по молекулярной физике и термодинамике
Курс лекций по молекулярной физике и термодинамике Аэродинамика
Аэродинамика Методологические основы и структура научного познания. Лекция №1
Методологические основы и структура научного познания. Лекция №1 Поля и взаимодействия. Лекция 01. Введение
Поля и взаимодействия. Лекция 01. Введение Гамма излучение
Гамма излучение Распространение радиоволн
Распространение радиоволн Электростатика. Электродинамика
Электростатика. Электродинамика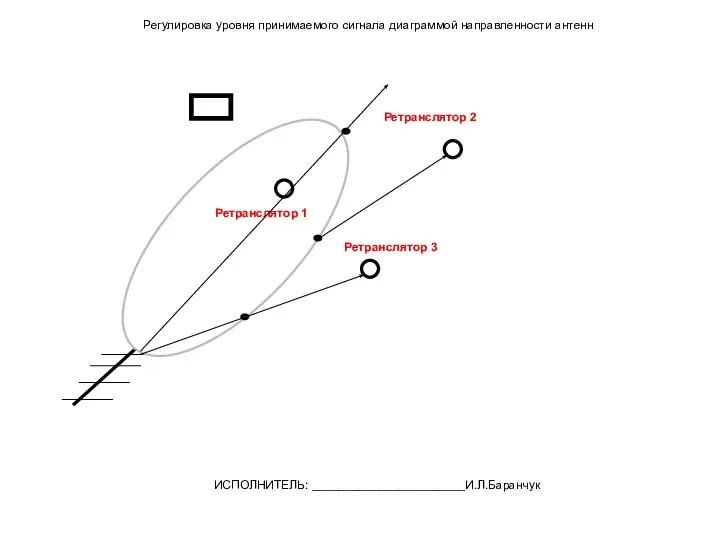 Регулировка уровня принимаемого сигнала диаграммой направленности антенн
Регулировка уровня принимаемого сигнала диаграммой направленности антенн Электромагнитные явления
Электромагнитные явления Звуковые волны. Свойства звука
Звуковые волны. Свойства звука Нерезьбовые соединения. Шпоночное соединение
Нерезьбовые соединения. Шпоночное соединение Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Развитие ядерной энергетики
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Развитие ядерной энергетики Распределение скоростей течения в речном потоке
Распределение скоростей течения в речном потоке Изучение магнитооптической дифракции в пленках ферритов-гранатов
Изучение магнитооптической дифракции в пленках ферритов-гранатов Приймачі світла
Приймачі світла Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю
Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю Физические основы механики. Лекция 1.1
Физические основы механики. Лекция 1.1 Курвиметр. Велокомпьютер с цифровым одометром
Курвиметр. Велокомпьютер с цифровым одометром 3. Работа и энергия
3. Работа и энергия