ВКБ-приближение. Общие соотношения

Если бы потенциал не зависел от координат, то решением УШ была бы плоская волна:
В случае слабой пространственной неоднородности потенциала решение УШ ищем в виде:
где показатель экспоненты имеет вид разложения по степеням постоянной Планка
Получить уравнения для функций и решить их?

Исходное уравнение для показателя экспоненты

Нулевое приближение
Решение
Потенциал не зависит от координат

Первое приближение

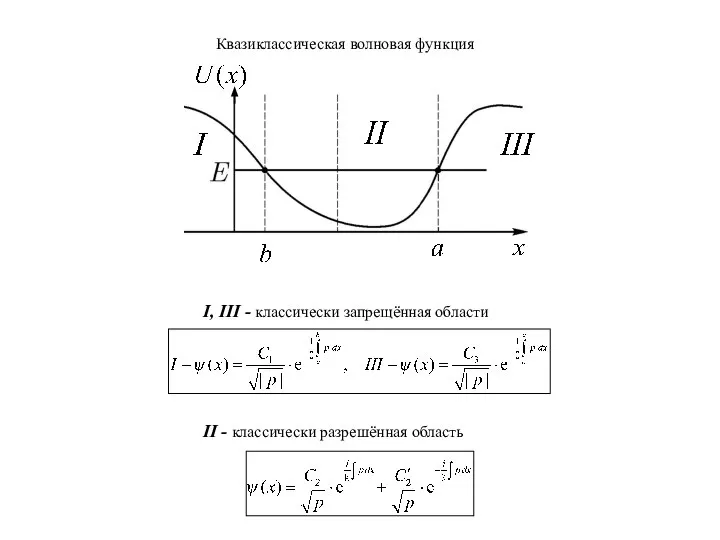
Квазиклассическая волновая функция
I, III - классически запрещённая области
II - классически разрешённая область

Условие применимости
Переписать условие применимости через параметры частицы и потенциала?

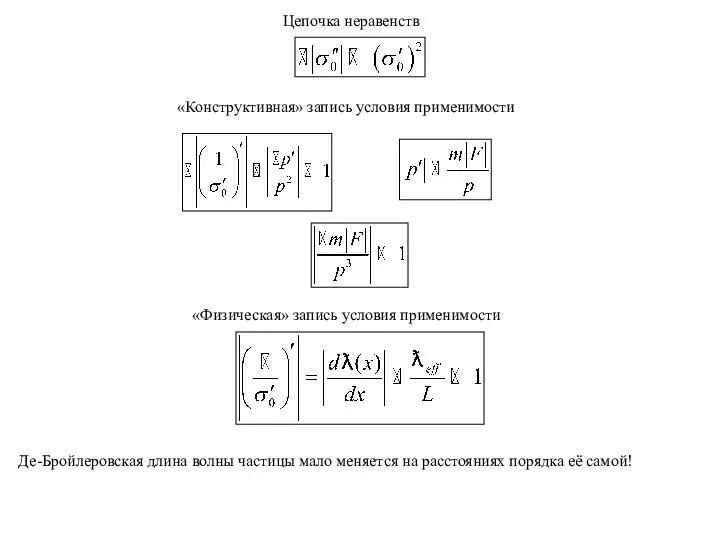
Цепочка неравенств
«Конструктивная» запись условия применимости
«Физическая» запись условия применимости
Де-Бройлеровская длина волны частицы мало меняется на расстояниях порядка её самой!

Условия сшивки в области точек остановки
В точках остановки импульс обращается в нуль и условие квазиклассичности нарушается!
УШ в окрестности точки остановки
Решение УШ – функции Эйри. Асимптотика в.ф.
Вопрос: можно ли использовать асимптотику функций Эйри в области
применимости квазиклассики?

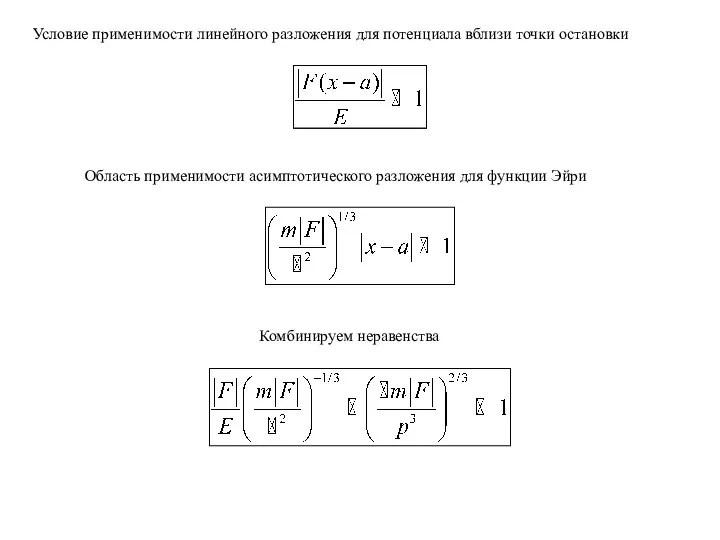
Условие применимости линейного разложения для потенциала вблизи точки остановки
Область применимости асимптотического разложения для функции Эйри
Комбинируем неравенства

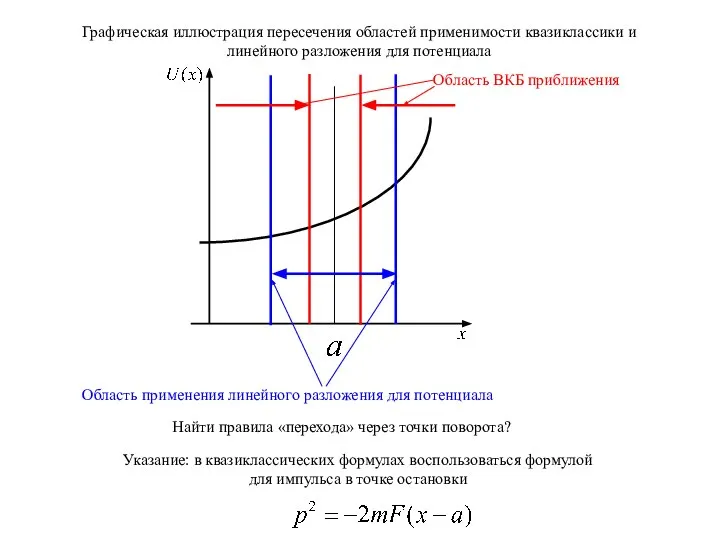
Графическая иллюстрация пересечения областей применимости квазиклассики и
линейного разложения для потенциала
Найти правила «перехода» через точки поворота?
Указание: в квазиклассических формулах воспользоваться формулой
для импульса в точке остановки

Правила «перехода» через точки остановки для потенциала типа «корыто»
«Переход» через правую точку остановки из области III в область II
«Переход» через левую точку остановки из области I в область II

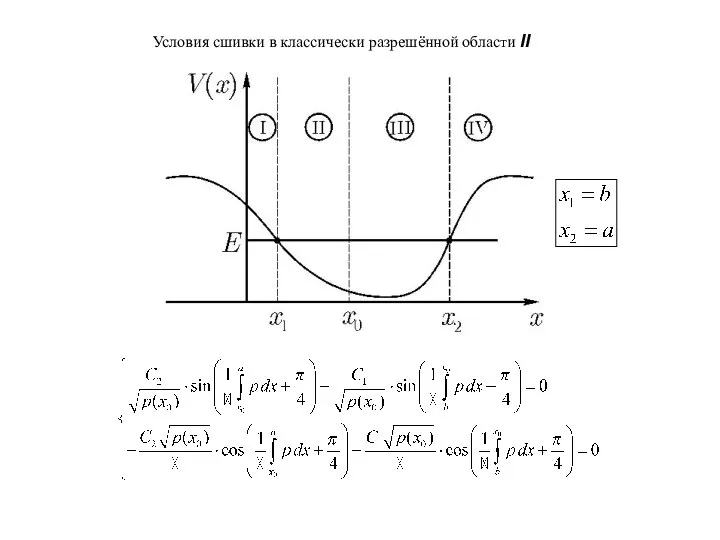
Правила квантования Бора-Зоммерфельда
Условия сшивки в классически разрешённой области II
Записать явный вид условий сшивки в квазиклассическом приближении?

Условия сшивки в классически разрешённой области II

Правила квантования Бора-Зоммерфельда
Или
Какое условие на величину n?

Интегралы по траекториям
(факультативно, подробности в книге Р.Фейнман, А.Хибс «Квантовая механика и интегралы
по траекториям»)
Качественные наводящие соображения
Амплитуда вероятности обнаружить частицу, находящуюся в квантовом состоянии n в точке
с координатой x:
Амплитуда вероятности обнаружить частицу, находящуюся в момент времени t0 в точке
с координатой x0 ,, в точке с координатой x в момент времени t:
В квазиклассическом приближении

Условие полноты
Амплитуда вероятности обнаружить частицу, находящуюся в момент времени t0 в точке
с координатой x0 ,, в точке с координатой x в момент времени t: