Волны. Уравнение плоской монохроматической бегущей волны. Колебания и волны. 9

Основные понятия теории волн
Процесс распространения деформаций в пространстве называется волной.
Чаще всего деформации носят характер колебаний. Эти колебания возбуждаются источником волны, поэтому являются вынужденными.

Основные понятия теории волн
Если распространяются механические колебания, то волну называют механической, если же распространяются колебания электрического и магнитного полей, то волну называют электромагнитной.
Период колебаний, возбужденных волной, называется периодом волны Т, а соответствующая частота колебаний – частотой волны ν.

Основные понятия теории волн
Если колебания, возбужденные волной, происходят вдоль направления распространения волны, волна называется продольной, если же колебания происходят поперек направления распространения волны, то волна называется поперечной.

Примеры:
1) звуковая волна в газах – продольная механическая;
2) волны в струнах, шнурах –поперечные механические, свет –поперечная электромагнитная волна.

Основные понятия теории волн
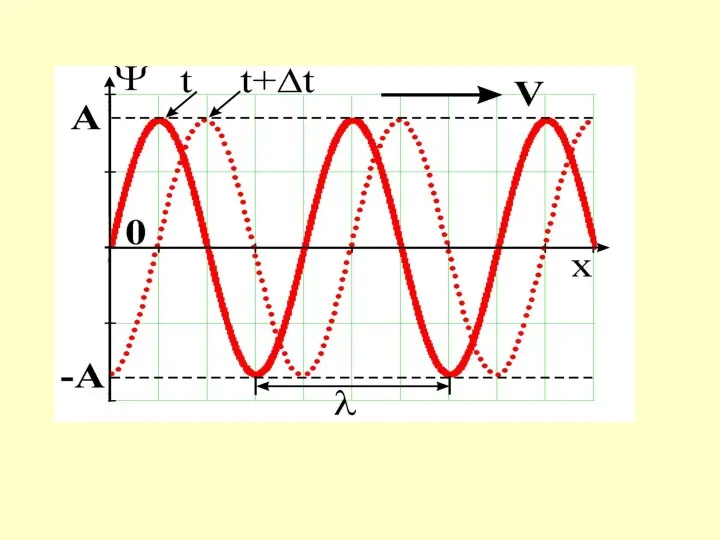
Опр.1. Расстояние между точками, колебания которых происходят с разностью фаз 2π радиан, называется длиной волны λ.
Опр.2. Расстояние, которое волна проходит за время, равное периоду колебаний Т, называется длиной волны λ.

Второе определение длины волны
позволяет получить связь между характеристиками волны:

Основные понятия теории волн
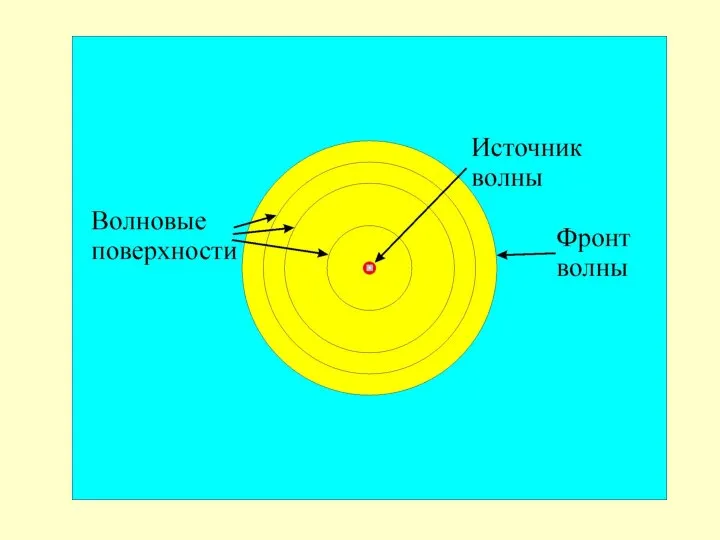
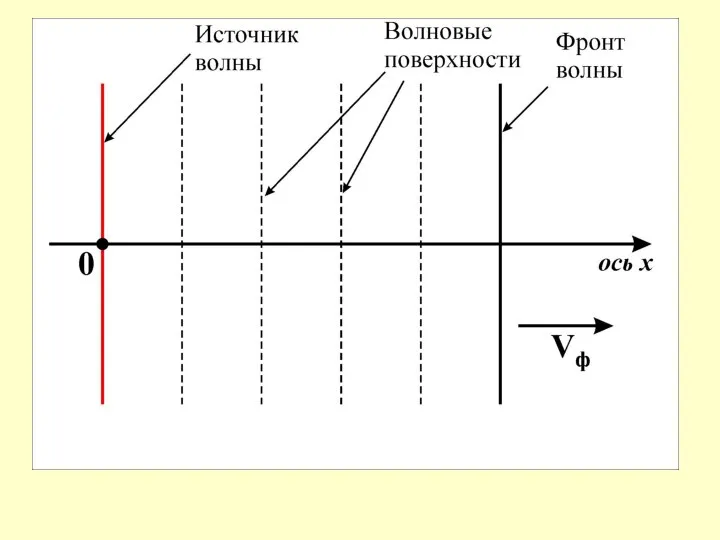
Поверхность, разделяющая область пространства, в которой волна уже есть, от области пространства, в которой волны еще нет, называется фронтом волны.
(Фронт волны перемещается в пространстве).
Поверхность, проходящая по положениям равновесия точек, которые колеблются в одинаковой фазе, называется волновой поверхностью.
(Волновая поверхность не перемещается в пространстве).

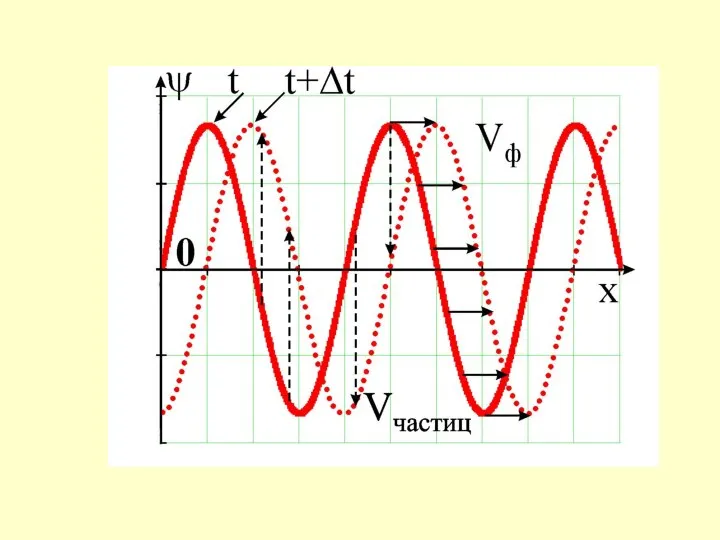
Основные понятия теории волн
Скорость перемещения в пространстве математической точки с определенным значением фазы волны, называется фазовой скоростью волны Vф.

Уравнение плоской монохроматической бегущей волны
Рассмотрим механическую волну с плоским фронтом. Пусть волна распространяется вдоль оси x от источника, расположенного в точке x = 0.
Зададим закон колебаний источника волны в виде
ψ(t) = Acos(ωt + ϕ).

Поставим задачу: найти смещение частиц, расположенных в точке с координатой x в момент времени t.
ψ( x , t ) = ?