ЯМР спектроскопия

Магнитные свойства микрочастиц
Если заряженная частица вращается вокруг некоторой
оси, то она проявляет магнитные свойства,
в частности обладает магнитным моментом (μ).

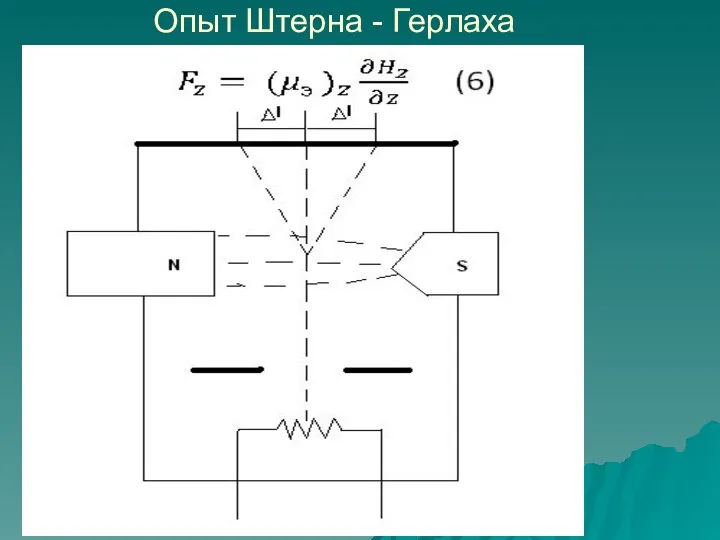
Опыт Штерна - Герлаха

Спиновое квантовое число (I)
N = 2I + 1 (7)
N – число подсистем во внешнем магнитном поле
(мультиплетность сигнала)
Для электрона: I = ½
Для 1Н: I = ½
Для 13С: I = ½
Для 31Р: I = ½
Для 2Н: I = 1

Правила предсказания спинового квантового числа (I)
1) Ядра с четным количеством и протонов и нейтронов имеют I = 0.
2) Ядра с нечетными числами и протонов и нейтронов имеют целочисленные значения спинового квантового числа I = 0, 1, 3…
3) Ядра с числами протонов и нейтронов разной четности имеют полуцелые значения спинового квантового числа (I = ½ ….)
½

Квантовомеханическая модель ЯМР
В основе квантовомеханической модели ЯМР лежит представление о взаимодействии магнитного момента (μ) с магнитным полем напряженностью (Н ). Энергия такого взаимодействия описывается уравнением Зеемана (8).

Квантовомеханическая модель ЯМР.
Вектор - спин

Переход между подуровнями
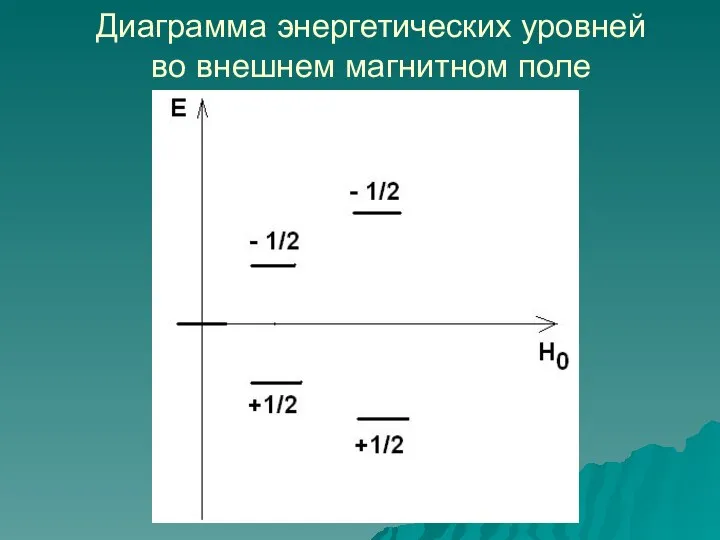
(для ядер со спиновым числом ½)

Диаграмма энергетических уровней во внешнем магнитном поле

Ядерным магнитным резонансом (ЯМР) называется явление резонансное поглощение энергии магнитными ядрами во внешнем магнитном поле

ЯМР на ансамбле магнитных ядер
Без внешнего магнитного
поля
В присутствии внешнего магнитного поля

Населенность энергетических уровней

Избыток заселенности. Сигнал ЯМР.

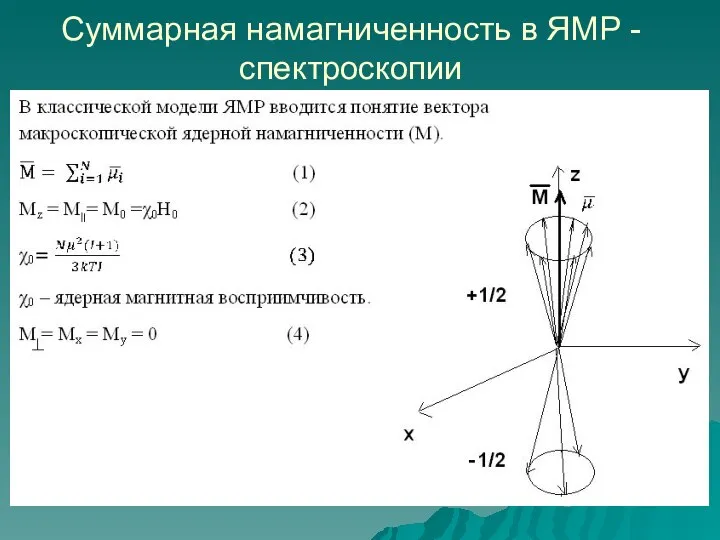
Суммарная намагниченность в ЯМР - спектроскопии

Теорема Лармора
Поведение системы, обладающей магнитным моментом (намагниченностью) М и пропорциональным ему механическим моментом Р, при наложении на эту систему магнитного поля можно представить как круговые движения (прецессию) вектора М в плоскости перпендикулярной направлению вектора магнитного поля Н0.
Частота прецессии определяется соотношением (5):

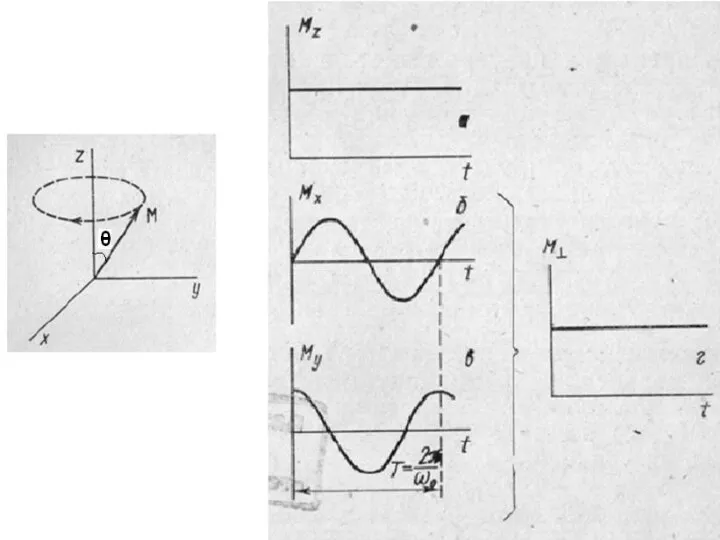
Проекции вектора макроскопической ядерной намагниченности

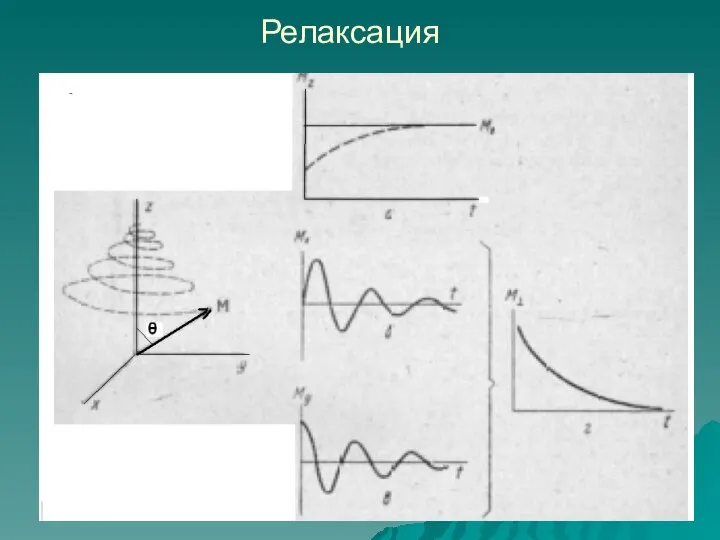
Релаксация

Продольная (спин-решеточная) релаксация

Поперечная (спин-спиновая) релаксация

ШИРИНА ЛИНИИ В ЯМР СПЕКТРЕ

Механизмы релаксации

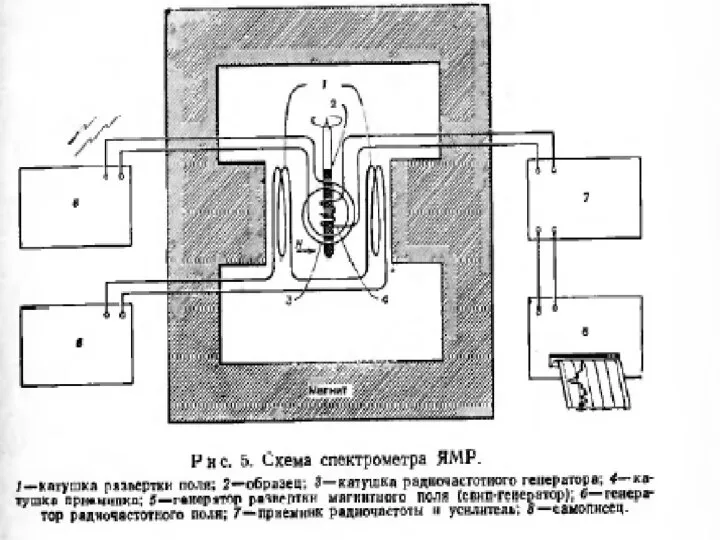
Принципы работы ЯМР - спектрометра
Вещество, содержащее магнитные ядра (I≠ 0) помещается в постоянное магнитное поле напряженностью Н0. В этом поле вектор суммарной ядерной намагниченности М совершает прецессию с частотой ( ω0 ). Внешнее магнитное поле однородно и имеет напряженность порядка нескольких Тл.
При частотной развертке (Н0 = соnst, ω - изменяется) Для возбуждения переходов между спиновыми подуровнями системы во внешнем магнитном поле Н0 прикладывается (перпендикулярно направлению вектора напряженности поля Н0 например по оси х)внешнее радиочастотное поле малой напряженности Н1 (Н1 << Н0) с изменяющейся частотой от ω1 < ω0 < ω2.
При полевой развертке (Н0 - изменяется, ω = соnst).

3) На оси у устанавливается катушка принимающая сигнал. В этой катушке возбуждается э.д.с. ядерной индукции, т.е. компоненты Му. Сигналы спада свободной индукции возникают при отключении внешнего магнитного поля Н0 за счет убыли компонент Мх и Му во времени. Сигнал спада свободной индукции по оси у содержит две компоненты:
Му = - usinωt + v соs ωt
u – сигнал дисперсии; v – сигнал поглощения
Сигнал поглощения детектируют и усиливают, он и несет информацию об интенсивности поглощения в ЯМР – спектре.

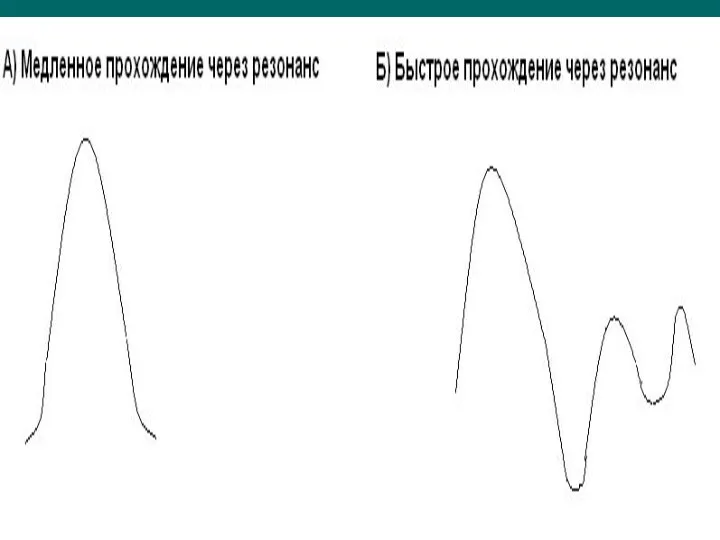
Быстрое и медленное прохождение через резонанс
Быстрое прохождение через резонанс
Резонанс реализуется в очень короткое время, что приводит к несовпадению частот прецессии векторов М и Н1. Последнее приводит к разфазировке, быстрому затуханию сигнала ЯМР и образованию виглей.
2) Медленное прохождение через резонанс
В этих условиях векторы М и Н1 длительное время сфазированы, что приводит к симметричным сигналам куполообразной формы.

Экранирование ядер
Согласно основному уравнению ЯМР, каждому ядру соответствует определенная частота резонанса, определяемая гиромагнитным отношением ядра и напряженностью внешнего магнитного поля, вызывающего зеемановское расщепление.
В молекулах одинаковые ядра одного сорта окружены различным электронным окружением. Это электронное окружение не статично (т.е. совершает движение) тем самым создавая переменное электрическое поле в пространстве. Взаимодействие внешнего магнитного поля (Н0) с полями создаваемыми электронами вблизи данного ядра, приводит к возникновению вторичного магнитного поля (Н’).

Константа экранирования
Нлок = Н0 – σН0 = (1- σ)Н0 (2)
σ – константа экранирования, характеризующая свойства данного ядра в данном электронном окружении.
Для атомов σ можно вычислить теоретически:

Стандарты в ЯМР
Пусть есть эталонное вещество Х, содержащее магнитные ядра исследуемого сорта, а также внутренний стандарт содержащий ядра того же сорта. В ЯМР 1Н и ЯМР 13С спектроскопии внутренним стандартом является тетраметилсилан (ТМС) (СН3)4Si.
ТМС удобен так как:
Дает интенсивный одиночный сигнал.
Поглощает в области где почти не проявляются другие сигналы.
Легко летуч и растворим в подавляющем большинстве органических растворителей.

Химический сдвиг ядра Х (в данном электронном окружении) (δх)

ЯМР 1Н (ПМР)

Концепция электроотрицательности
Экранирование ядра тем больше, чем больше электронная плотность на нем.
Введение электроноакцепторных заместителей должно приводить к дезэкранированию (увеличению химического сдвига сигнала, сдвигу сигнала в слабое поле), а введение электронодонорных заместителей приводит к обратному эффекту.
Правило: с увеличением электроотрицательности группы А в фрагмента -СН2 – СН – А, химический сдвиг α-протона увеличивается (α-эффект), а химический сдвиг β-протона уменьшается (β-эффект).

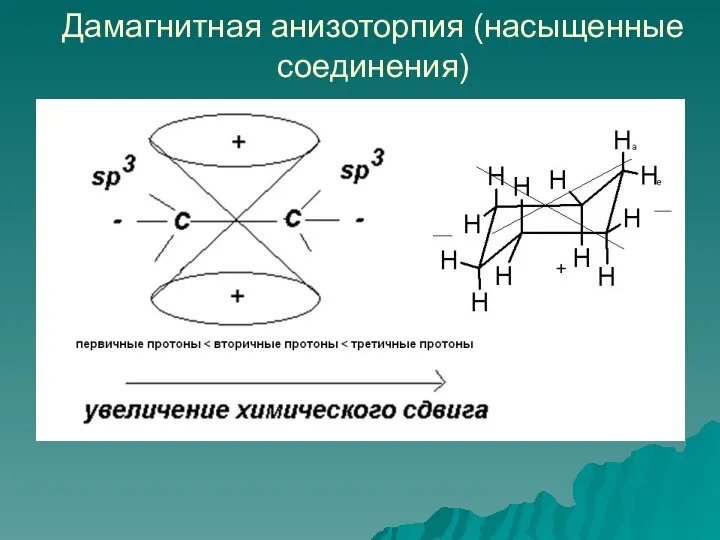
Диамагнитная анизотропия
Некоторые группы обладают различными магнитными восприимчивостями по различным направлениям, что определяет анизотропию вторичного магнитного поля и как следствие анизотропию локальных магнитных полей вблизи магнитных ядер, что проявляется в дополнительном изменение химического сдвига.
Изменение химического сдвига за счет диамагнитной анизотропии равносильно изменению константы экранирования (σ).
Δσ =Δχ(1-3cosθ)/3R3
Δχ =χпарал -χперп
R – расстояние от диполя до рассматриваемого угла.
Θ – угол между векторами (R) и осью аксиальной симметрии.

Дамагнитная анизоторпия (насыщенные соединения)

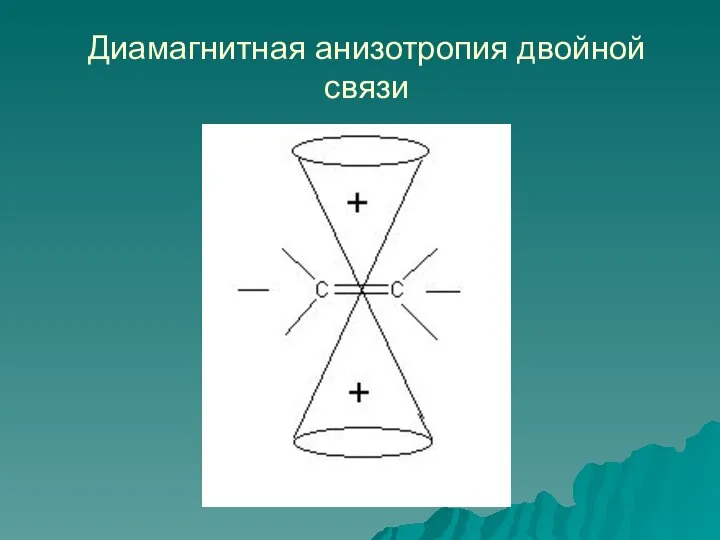
Диамагнитная анизотропия двойной связи

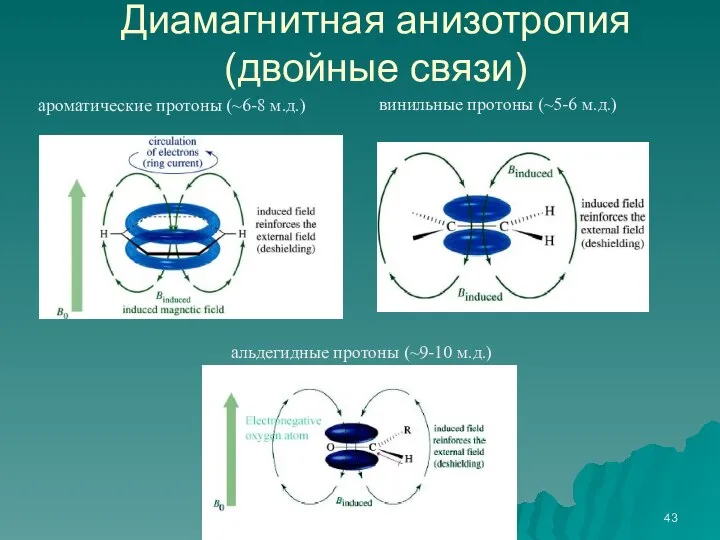
ароматические протоны (~6-8 м.д.)
винильные протоны (~5-6 м.д.)
альдегидные протоны (~9-10 м.д.)
Диамагнитная анизотропия (двойные связи)

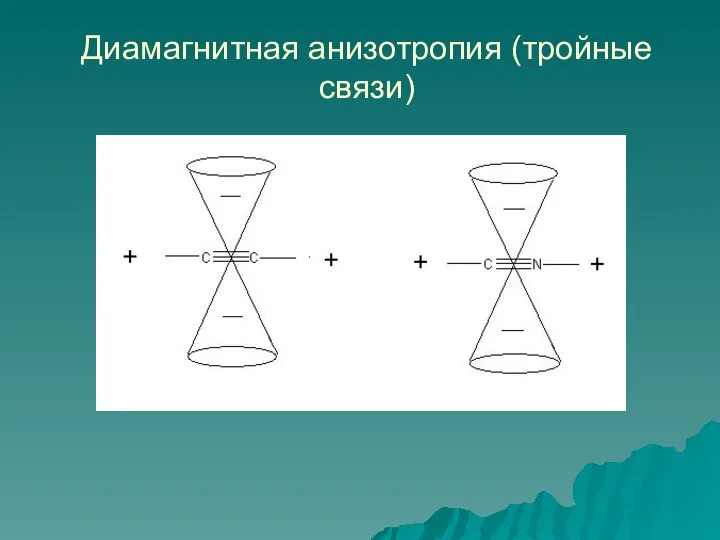
Диамагнитная анизотропия (тройные связи)