Содержание
- 2. б) распределение по поверхности в) распределение по объему а) линейное распределение Равномерно распределенный заряд
- 3. обнаруживают по действию на заряженные тела проводники с током, рамки с током или магнитные стрелки Закон
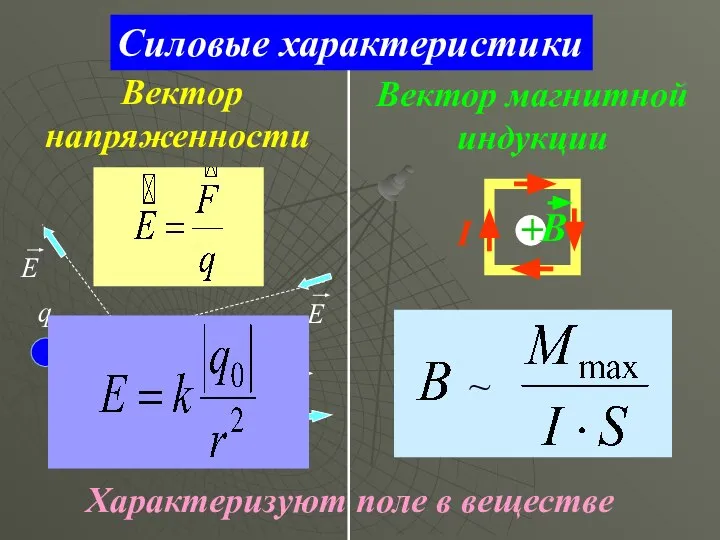
- 4. Силовые характеристики Вектор напряженности q0 q0 Вектор магнитной индукции I Характеризуют поле в веществе
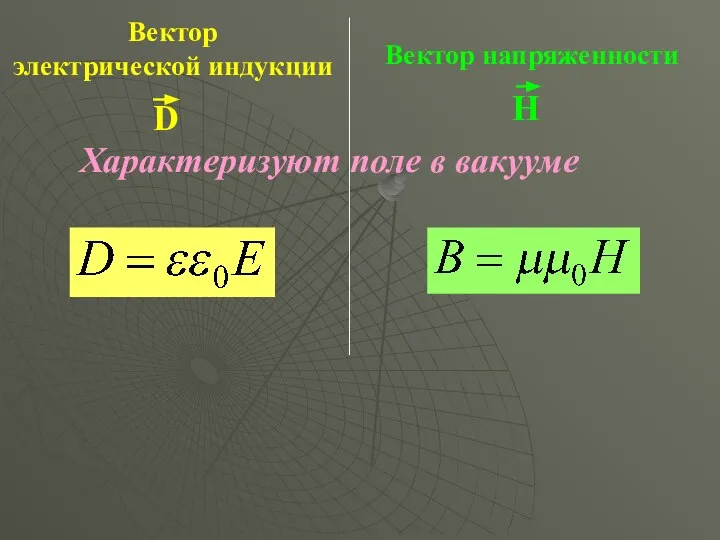
- 5. Вектор электрической индукции Вектор напряженности Характеризуют поле в вакууме
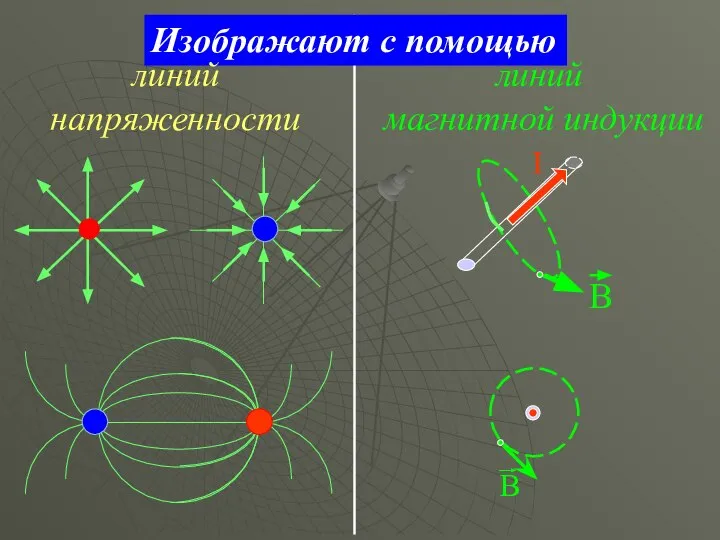
- 6. I Изображают с помощью линий магнитной индукции линий напряженности
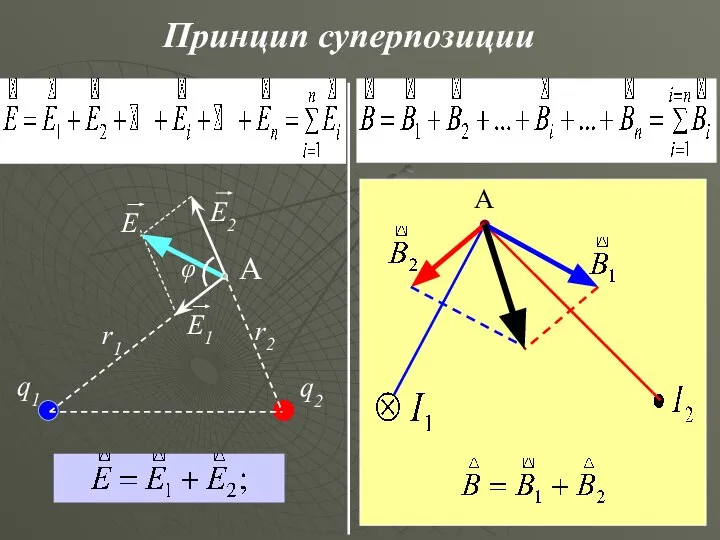
- 7. Принцип суперпозиции q1 q2 r1 r2 φ А А
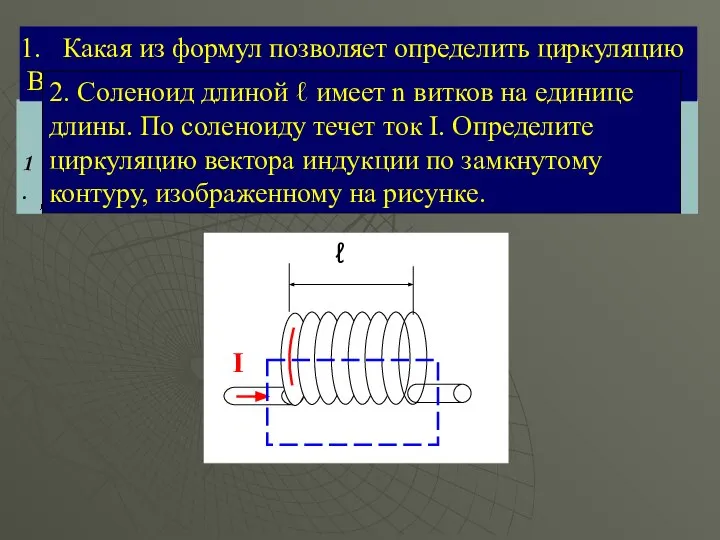
- 9. Закон Био-Савара-Лапласа (БСЛ) I A dℓ I R r x β X Y dB
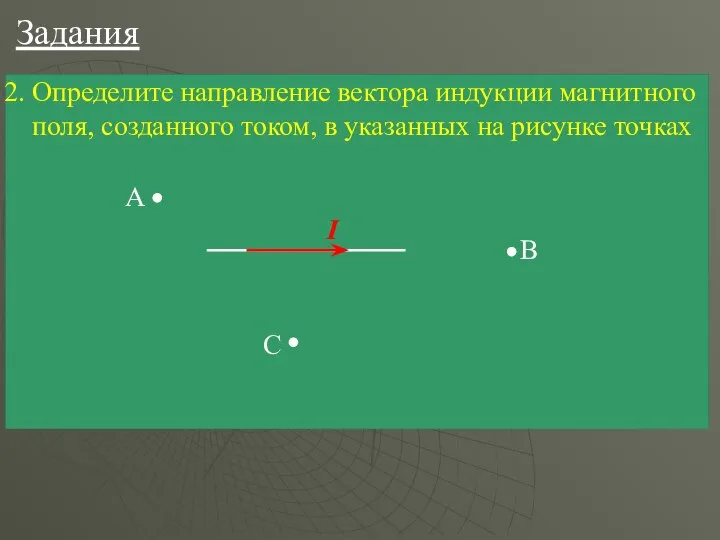
- 10. Задания
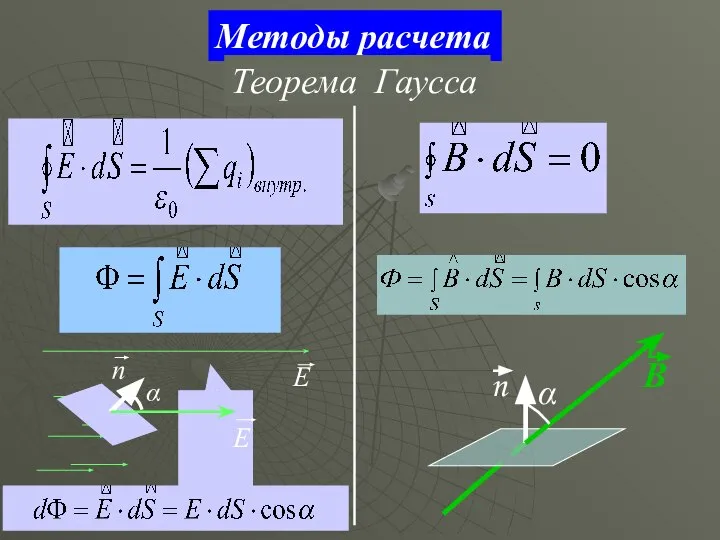
- 11. Методы расчета Теорема Гаусса α
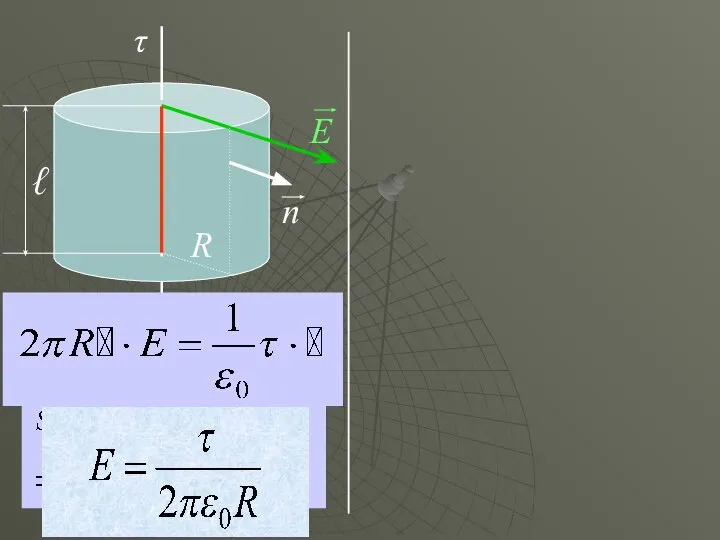
- 12. τ ℓ R
- 13. 1. Определите поток вектора напряженности через замкнутую поверхность для случая, изображенного на рисунке. 2. Стержень длиной
- 14. Теорема о циркуляции Поле потенциально Поле непотенциально I B r
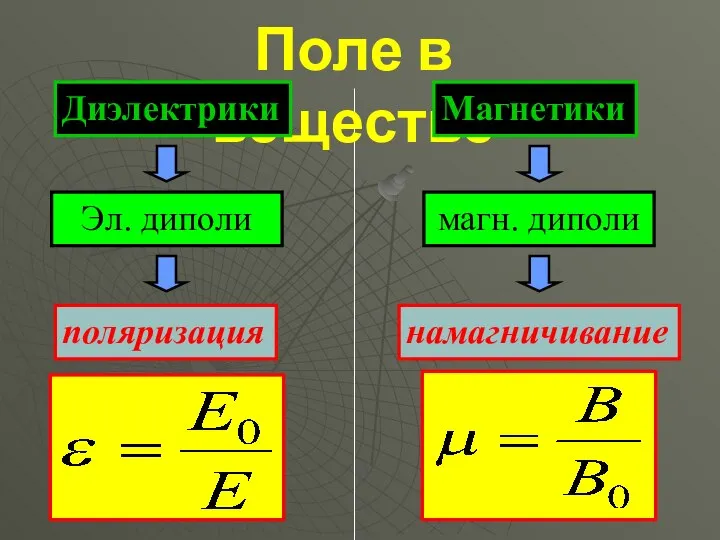
- 15. Поле в веществе Диэлектрики поляризация Эл. диполи Магнетики магн. диполи намагничивание
- 16. Энергия поля
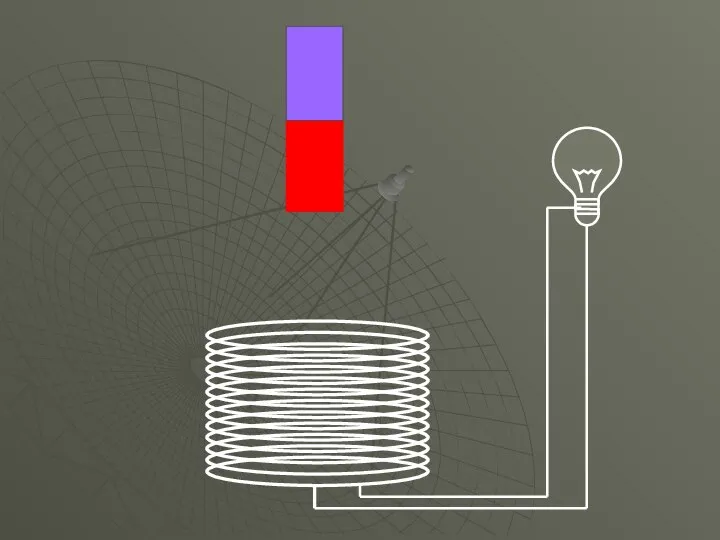
- 18. Явление электромагнитной индукции
- 20. Закон электромагнитной индукции Фарадея. Среднее значение э.д.с. в интервале времени Для простого контура: Для сложного контура:
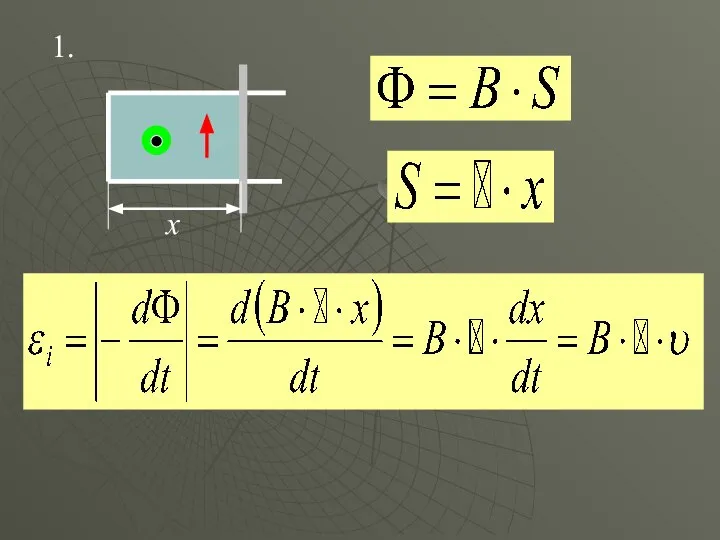
- 21. Мгновенное значение э.д.с. индукции в момент времени t: Для простого контура: Для сложного контура:
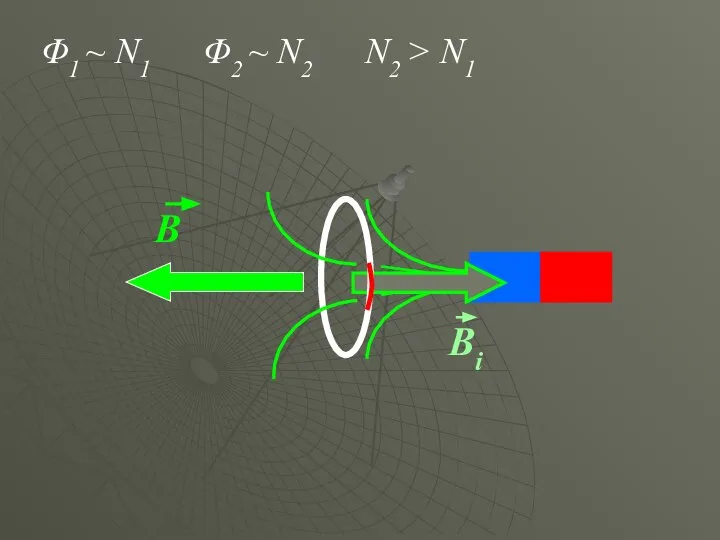
- 22. Φ1 ~ N1 Φ2 ~ N2 N2 > N1
- 23. 1. x
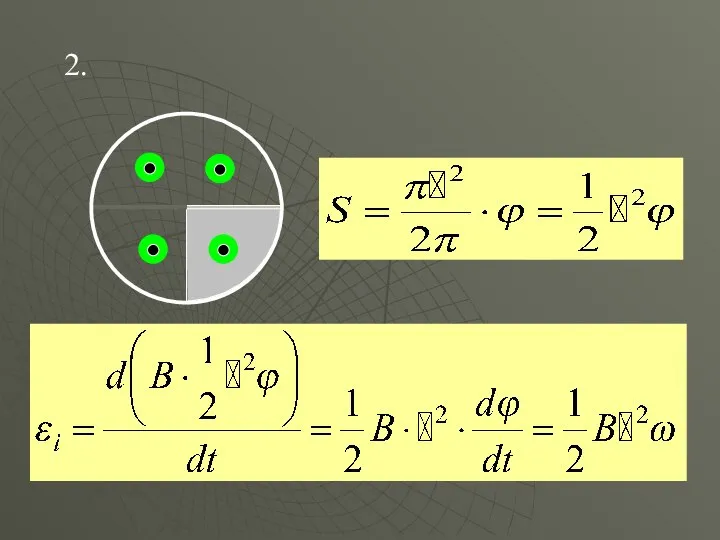
- 24. 2.
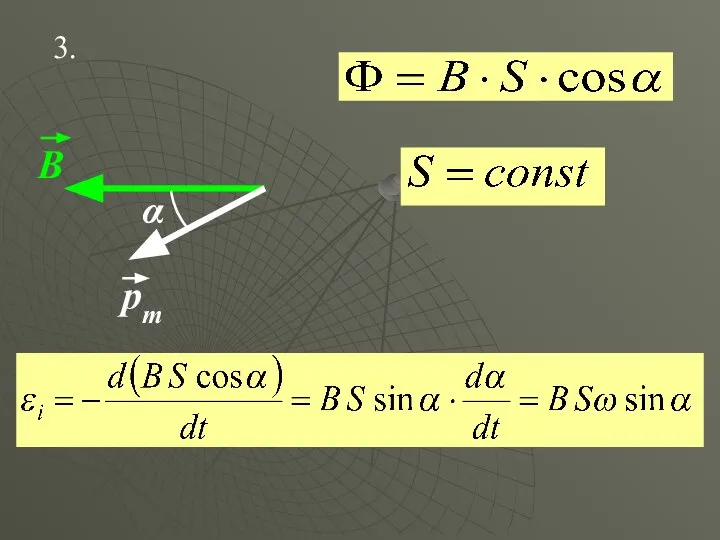
- 25. 3. α
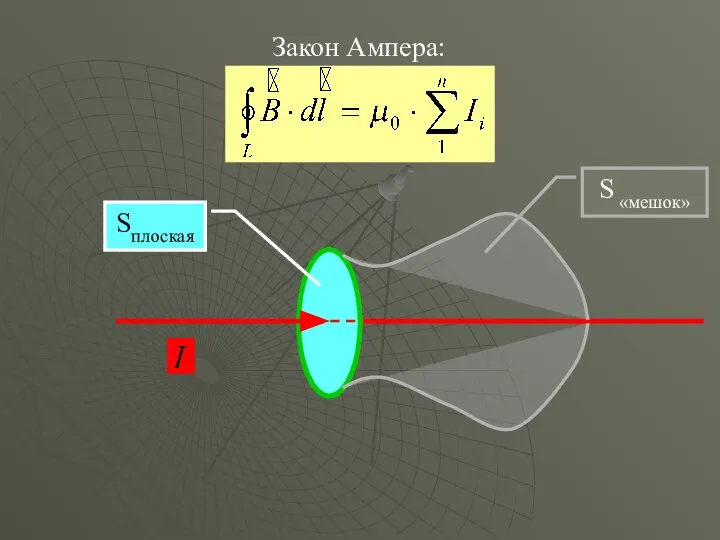
- 26. Закон Ампера: Sплоская S «мешок»
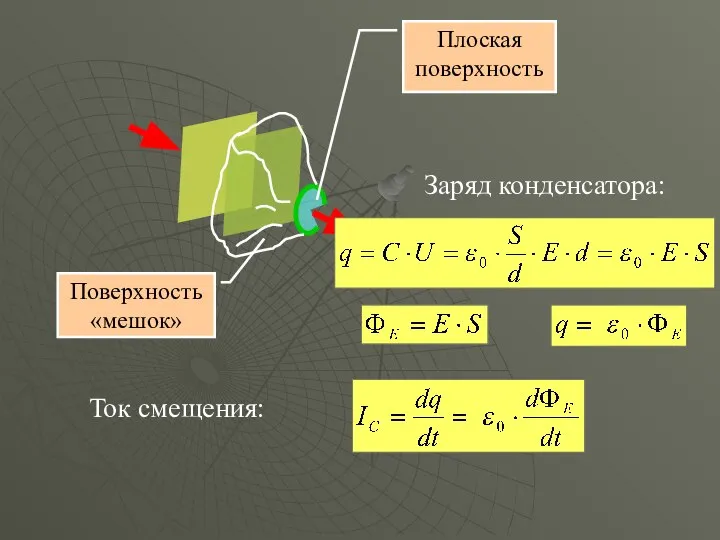
- 27. Плоская поверхность Поверхность «мешок» Заряд конденсатора: Ток смещения:
- 28. Поле неоднородное:
- 29. Закон Ампера с учётом тока смещения:
- 30. Обобщенный закон Фарадея: Переменное магнитное поле Электрическое поле Магнитное поле Переменное электрическое поле
- 31. Система уравнений Максвелла:
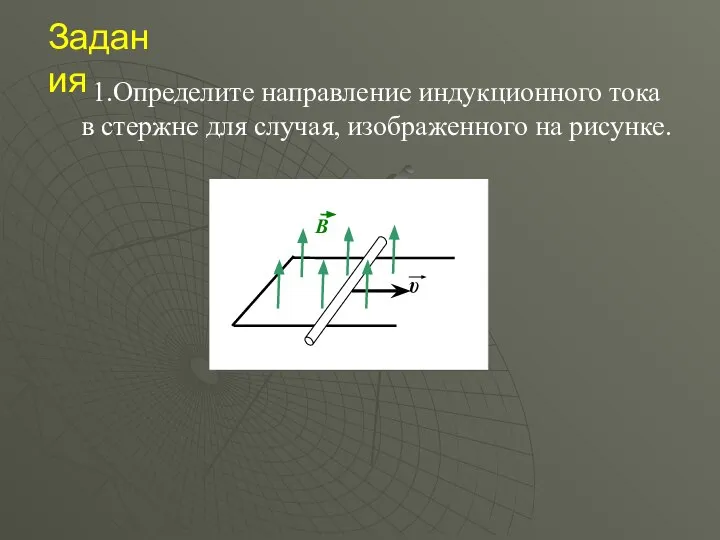
- 32. Задания 1.Определите направление индукционного тока в стержне для случая, изображенного на рисунке.
- 34. Скачать презентацию














 Устройство легкового автомобиля и величина тормозного пути транспортного средства
Устройство легкового автомобиля и величина тормозного пути транспортного средства Презентация на тему Радиоактивные превращения атомных ядер
Презентация на тему Радиоактивные превращения атомных ядер  Что такое энергия?
Что такое энергия? Примеры решения задач. Водородоподобные атомы. Оптические спектры излучения
Примеры решения задач. Водородоподобные атомы. Оптические спектры излучения Текстура. Лекция 2
Текстура. Лекция 2 Презентация на тему Что такое свет? Корпускулярно-волновой дуализм
Презентация на тему Что такое свет? Корпускулярно-волновой дуализм  Никола Тесла и его электричество
Никола Тесла и его электричество Интерактивная игра по физике. Морской бой
Интерактивная игра по физике. Морской бой Свободное падение тел_ Движение с ускорением свободного падения
Свободное падение тел_ Движение с ускорением свободного падения Инженер древности Герон Александрийский
Инженер древности Герон Александрийский Свинцово-кислотные аккумуляторы
Свинцово-кислотные аккумуляторы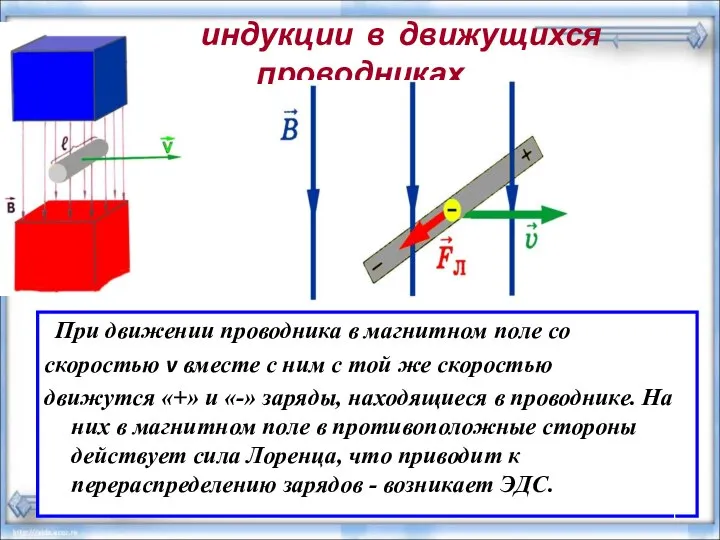 Вихревое электрическое поле. ЭДС индукции в движущихся проводниках
Вихревое электрическое поле. ЭДС индукции в движущихся проводниках Инновационные технологии в машиностроении. Лекция 1, 2. Общая характеристика машиностроительного производства
Инновационные технологии в машиностроении. Лекция 1, 2. Общая характеристика машиностроительного производства Законы сохранения в механике
Законы сохранения в механике Принцип суперпозиции полей
Принцип суперпозиции полей Техника Победы. Автомобиль ЗИС - 5 (трёхтонка, Захар, Захар Иванович)
Техника Победы. Автомобиль ЗИС - 5 (трёхтонка, Захар, Захар Иванович) Интерференция волн
Интерференция волн Зависимость давления твердых тел от силы давления и от площади поверхности, на которую действует сила давления
Зависимость давления твердых тел от силы давления и от площади поверхности, на которую действует сила давления Спектірлік анализ әдістері
Спектірлік анализ әдістері Основные понятия и законы динамики
Основные понятия и законы динамики Магнитное поле
Магнитное поле Блоки цилиндров и цилиндровые втулки
Блоки цилиндров и цилиндровые втулки Сущность и применение метода импеданса с помощью прибора БакТрак для определения различных групп микроорганизмов
Сущность и применение метода импеданса с помощью прибора БакТрак для определения различных групп микроорганизмов Неисправности двигателя Gamma. KIA Motors
Неисправности двигателя Gamma. KIA Motors Основное уравнение динамики вращательного движения твердого тела. (Лекция 7)
Основное уравнение динамики вращательного движения твердого тела. (Лекция 7) Линза. Построение изображения в линзе
Линза. Построение изображения в линзе Тема: Полупроводники Цель: изучить проводимость полупроводников
Тема: Полупроводники Цель: изучить проводимость полупроводников Работа, мощность. Энергия
Работа, мощность. Энергия