Содержание
- 2. 1.3 Возбуждение перехода между спиновыми состояниями Между двумя рассматриваемыми уровнями возможны переходы, сопровождающиеся поглощением или испусканием
- 3. Основное уравнение ЯМР Подставляя выражение ΔЕ из уравнения (6) в соотношение (7), получаем основное уравнение ЯМР,
- 4. Резонансная частота для протона Для протона, находящегося в магнитном поле с индукцией 1,41 Тл, эта частота
- 5. 1.4 Разность между энергиями спиновых состояний Основная проблема метода состоит в том, как заставить протон, сориентированный
- 6. 1.5 Физические основы ЯМР Пусть имеются множество однотипных ядер со спином I = 1/2 (например, протонов),
- 7. Населенность спиновых состояний Многочисленные экспериментальные данные показывают, что заселенности уровней подчиняются так называемому статистическому распределению Больцмана
- 8. Населенность спиновых состояний В условиях равновесия заселенность нижнего энергетического уровня В2 окажется несколько большей, чем В1.
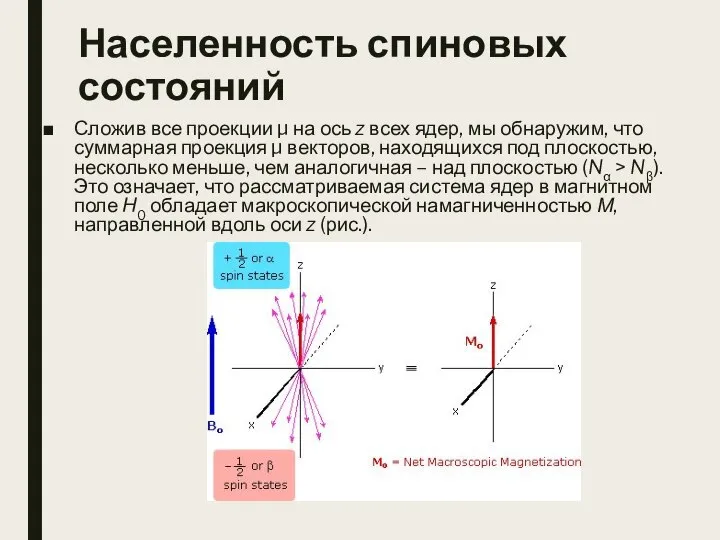
- 9. Населенность спиновых состояний Сложив все проекции μ на ось z всех ядер, мы обнаружим, что суммарная
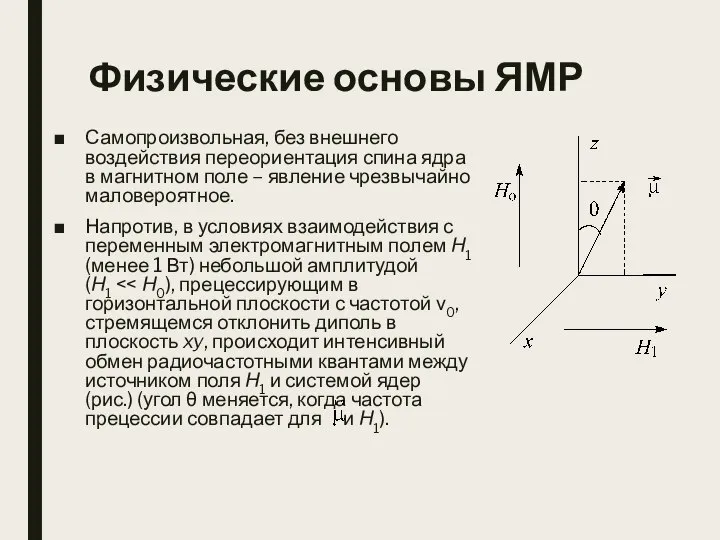
- 10. Физические основы ЯМР Самопроизвольная, без внешнего воздействия переориентация спина ядра в магнитном поле – явление чрезвычайно
- 11. Физические основы ЯМР Каждая переориентация вектора магнитного момента ядер сопровождается испусканием или поглощением кванта энергии hν
- 12. Чувствительность спектроскопии ЯМР 13С и 1Н Если сравнивать чувствительность 13С и 1Н при одинаковом внешнем магнитном
- 13. Чувствительность спектроскопии ЯМР 13С и 1Н Наиболее очевидным путем повышения интенсивности сигнала является использование более сильных
- 14. Чувствительность спектроскопии ЯМР 13С и 1Н Многократное сканирование (благодаря накоплению и усреднению спектров) позволяет снизить уровень
- 15. Химический сдвиг Нинд = σ·Н0, (16) где σ – коэффициент пропорциональности, называемый константой экранирования. Теперь напряженность
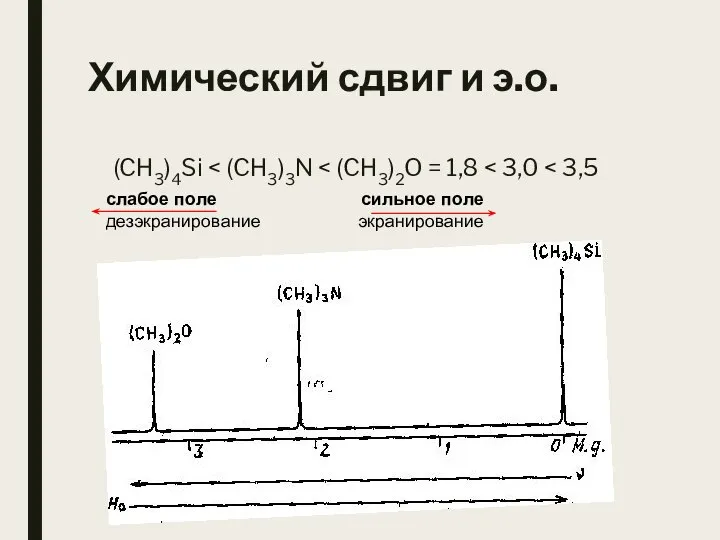
- 16. Химический сдвиг и э.о. (CH3)4Si слабое поле дезэкранирование сильное поле экранирование
- 17. Химический сдвиг: м.д. и тау-шкала Химический сдвиг – разность расстояний между двумя линиями в спектре, выраженная
- 19. Скачать презентацию













 Регулярные вариации низкочастотных акустических полей
Регулярные вариации низкочастотных акустических полей Электрическая цепь и ее составные
Электрическая цепь и ее составные Колебательный контур
Колебательный контур Квантовая природа света
Квантовая природа света Радиационное излучение
Радиационное излучение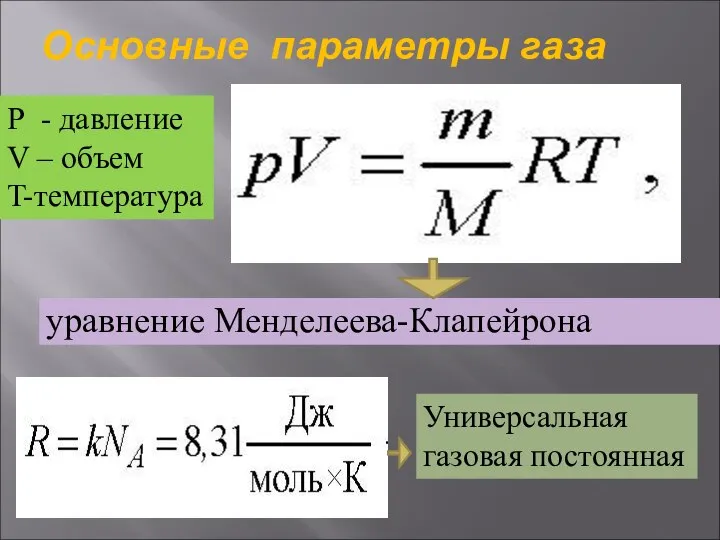 Основные параметры газа
Основные параметры газа Способы соединения частей: шестеренки
Способы соединения частей: шестеренки Явление тяготения. Сила тяжести
Явление тяготения. Сила тяжести Лазеры. Виды лазеров
Лазеры. Виды лазеров Альбом электрических схем для сдачи экзаменов по программе Машинист электропоезда
Альбом электрических схем для сдачи экзаменов по программе Машинист электропоезда Системы высот. Геодезия
Системы высот. Геодезия Классификация тепловых двигателей
Классификация тепловых двигателей Проведение прочностных расчетов машин и механизмов на предприятии
Проведение прочностных расчетов машин и механизмов на предприятии Попов – основатель радиовещания
Попов – основатель радиовещания Обобщающий урок Знатоки физики
Обобщающий урок Знатоки физики Техническое обслуживание смазочной системы МТЗ-80
Техническое обслуживание смазочной системы МТЗ-80 Простые механизмы. КПД
Простые механизмы. КПД Урок4 РПД
Урок4 РПД Презентация на тему Инерция и инертность
Презентация на тему Инерция и инертность  Наблюдение сплошного и линейчатых спектров. Лабораторная работа
Наблюдение сплошного и линейчатых спектров. Лабораторная работа Полупроводники
Полупроводники OVZ_Zanyatie_3
OVZ_Zanyatie_3 Энергия колебательного движения
Энергия колебательного движения Современные требования к проектной документации по размещению передающих радиотехнических объектов
Современные требования к проектной документации по размещению передающих радиотехнических объектов Презентация на тему Колебательный контур. Электромагнитные колебания
Презентация на тему Колебательный контур. Электромагнитные колебания  Презентация на тему Теплопередача и ее виды
Презентация на тему Теплопередача и ее виды  Основное уравнение динамики вращательного движения твердого тела. (Лекция 7)
Основное уравнение динамики вращательного движения твердого тела. (Лекция 7) Физика плазмы
Физика плазмы