Содержание
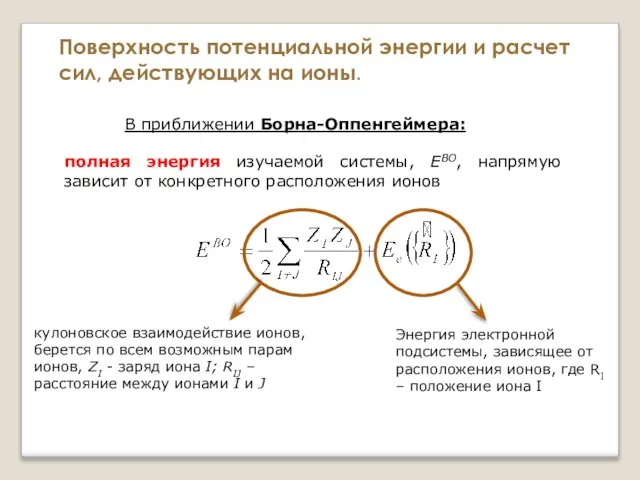
- 2. полная энергия изучаемой системы, EBO, напрямую зависит от конкретного расположения ионов Поверхность потенциальной энергии и расчет
- 3. Атомистические и микроскопические методы Молекулярная статика Молекулярная динамика Главной задачей является нахождение состояния системы с минимальной
- 4. Молекулярная динамика
- 5. Молекулярная динамика (МД) − это метод компьютерного моделирования, позволяющий проследить эволюцию системы взаимодействующих частиц во времени
- 6. Молекулярная динамика (МД) − это метод компьютерного моделирования, позволяющий проследить эволюцию системы взаимодействующих частиц во времени
- 7. Молекулярная динамика (МД) − это метод компьютерного моделирования, позволяющий проследить эволюцию системы взаимодействующих частиц во времени
- 8. Молекулярная динамика (МД) − это метод компьютерного моделирования, позволяющий проследить эволюцию системы взаимодействующих частиц во времени
- 9. Молекулярная динамика (МД) − это метод компьютерного моделирования, позволяющий проследить эволюцию системы взаимодействующих частиц во времени
- 10. Основы метода молекулярной динамики В материаловедческих приложениях, МД применяется для: изучения динамики кристаллической решетки материалов,
- 11. Основы метода молекулярной динамики В материаловедческих приложениях, МД применяется для: изучения динамики кристаллической решетки материалов, моделирования
- 12. Основы метода молекулярной динамики В материаловедческих приложениях, МД применяется для: изучения динамики кристаллической решетки материалов, моделирования
- 13. Основы метода молекулярной динамики В материаловедческих приложениях, МД применяется для: изучения динамики кристаллической решетки материалов, моделирования
- 14. Основы метода молекулярной динамики В материаловедческих приложениях, МД применяется для: изучения динамики кристаллической решетки материалов, моделирования
- 15. Основы метода молекулярной динамики Метод молекулярной динамики по сравнению с другими методами компьютерного моделирования обладает несколькими
- 16. Основы метода молекулярной динамики Метод молекулярной динамики по сравнению с другими методами компьютерного моделирования обладает несколькими
- 17. Основы метода молекулярной динамики Метод молекулярной динамики по сравнению с другими методами компьютерного моделирования обладает несколькими
- 18. Основы метода молекулярной динамики Метод молекулярной динамики по сравнению с другими методами компьютерного моделирования обладает несколькими
- 19. Основы метода молекулярной динамики Основная идея метода МД - поведение заданной совокупности атомов описывается в рамках
- 20. Основы метода молекулярной динамики Основная идея метода МД - поведение заданной совокупности атомов описывается в рамках
- 21. Основы метода молекулярной динамики Основная идея метода МД - поведение заданной совокупности атомов описывается в рамках
- 22. Основы метода молекулярной динамики Основная идея метода МД - поведение заданной совокупности атомов описывается в рамках
- 23. Основы метода молекулярной динамики Основная идея метода МД - поведение заданной совокупности атомов описывается в рамках
- 24. Основы метода молекулярной динамики Основная идея метода МД - поведение заданной совокупности атомов описывается в рамках
- 25. Основы метода молекулярной динамики Основная идея метода МД - поведение заданной совокупности атомов описывается в рамках
- 26. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Начальные значения координат атомов задаются в зависимости от
- 27. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. При решении задач молекулярной динамики осуществляется контроль над
- 28. Основы метода молекулярной динамики Молекулярная динамика относится к классу детерминистических методов
- 29. Основы метода молекулярной динамики Молекулярная динамика относится к классу детерминистических методов: при однозначно определенных (заданных) начальных
- 30. Основы метода молекулярной динамики Молекулярная динамика относится к классу детерминистических методов: при однозначно определенных (заданных) начальных
- 31. Основы метода молекулярной динамики Молекулярная динамика относится к классу детерминистических методов: при однозначно определенных (заданных) начальных
- 32. Основы метода молекулярной динамики Чаще, молекулярная динамика используется в качестве метода статистической механики, что оправдано для
- 33. Основы метода молекулярной динамики Чаще, молекулярная динамика используется в качестве метода статистической механики, что оправдано для
- 34. Основы метода молекулярной динамики Чаще, молекулярная динамика используется в качестве метода статистической механики, что оправдано для
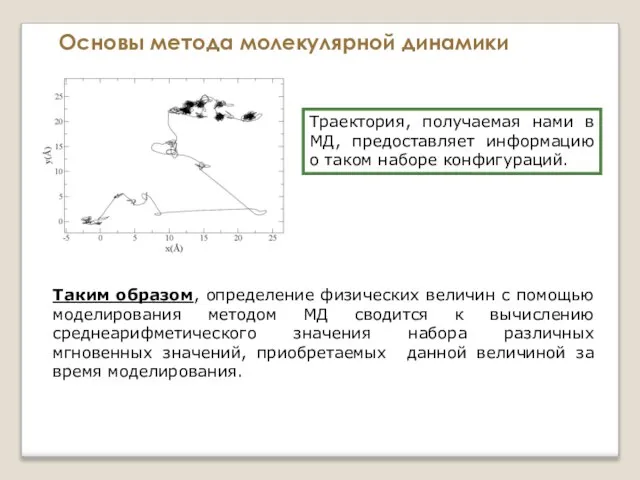
- 35. Основы метода молекулярной динамики Траектория, получаемая нами в МД, предоставляет информацию о таком наборе конфигураций. Таким
- 36. Основы метода молекулярной динамики Ограничения МД 1. МД чувствителен к выбору способа описания межатомных взаимодействий (межатомного
- 37. Основы метода молекулярной динамики Ограничения МД 1. МД чувствителен к выбору способа описания межатомных взаимодействий (межатомного
- 38. Основы метода молекулярной динамики Ограничения МД МД чувствителен к выбору способа описания межатомных взаимодействий (межатомного потенциала
- 39. Основы метода молекулярной динамики Ограничения МД МД чувствителен к выбору способа описания межатомных взаимодействий (межатомного потенциала
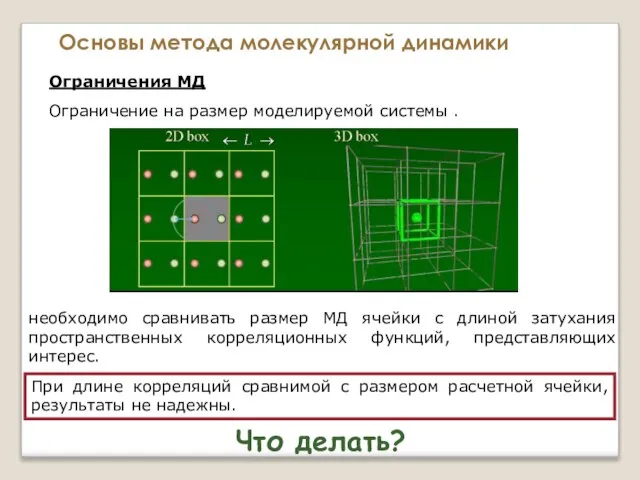
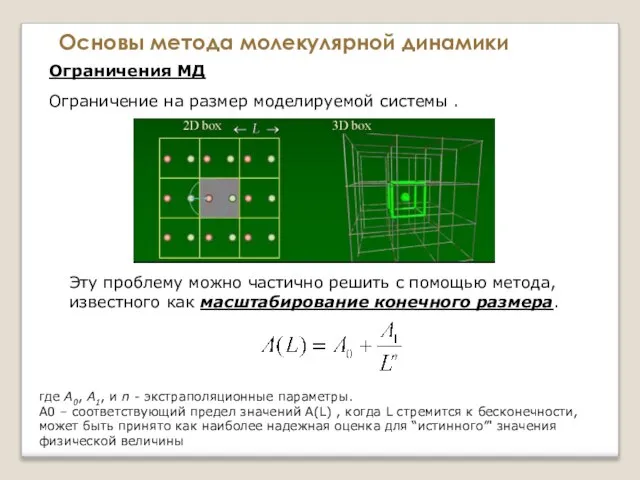
- 40. Основы метода молекулярной динамики Ограничения МД Ограничение на размер моделируемой системы . необходимо сравнивать размер МД
- 41. Основы метода молекулярной динамики Ограничения МД Ограничение на размер моделируемой системы . необходимо сравнивать размер МД
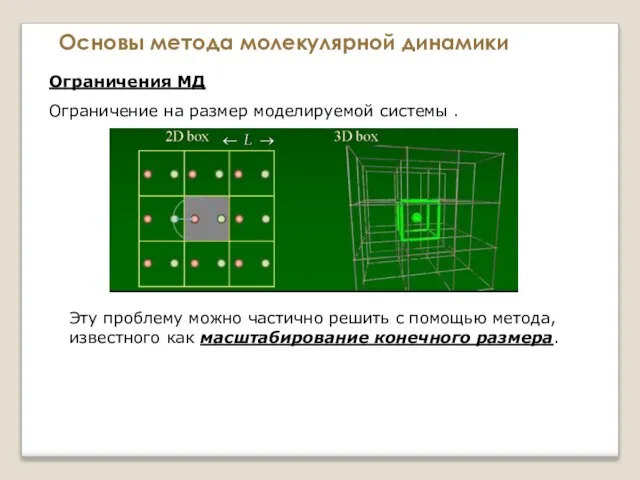
- 42. Основы метода молекулярной динамики Ограничения МД Ограничение на размер моделируемой системы . Эту проблему можно частично
- 43. Основы метода молекулярной динамики Ограничения МД Ограничение на размер моделируемой системы . Эту проблему можно частично
- 44. Основы метода молекулярной динамики Типичная последовательность шагов для МД моделирования: Создание модели кристалла; Релаксация полученной системы
- 45. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Используемые алгоритмы интегрирования уравнений Ньютона, как правило, основаны
- 46. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Используемые алгоритмы интегрирования уравнений Ньютона, как правило, основаны
- 47. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Используемые алгоритмы интегрирования уравнений Ньютона, как правило, основаны
- 48. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Рассмотрим одномерное движение частицы и запишем уравнения Ньютона
- 49. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Конечно-разностные методы, как правило, основаны на разложении в
- 50. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. В простейшем методе Эйлера остаются только члены О(Δt)
- 51. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. В простейшем методе Эйлера остаются только члены О(Δt)
- 52. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. В простейшем методе Эйлера остаются только члены О(Δt)
- 53. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Для уменьшения энергетических флуктуаций, на величину Δt накладывают
- 54. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Метод Эйлера является асимметричным, поскольку он продвигает решение
- 55. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Устойчивость численного решения можно контролировать в случае, когда
- 56. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Устойчивость численного решения можно контролировать в случае, когда
- 57. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Устойчивость численного решения можно контролировать в случае, когда
- 58. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Устойчивость численного решения можно контролировать в случае, когда
- 59. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. В выражениях для xn+1 и υn+1 остались члены
- 60. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Наиболее известным из методов, обеспечивающих более точное соблюдение
- 61. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Наиболее известным из методов, обеспечивающих более точное соблюдение
- 62. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Наиболее известным из методов, обеспечивающих более точное соблюдение
- 63. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Складывая эти два выражения, получаем основное выражение алгоритма
- 64. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Складывая эти два выражения, получаем основное выражение алгоритма
- 65. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Плюсы алгоритма Верле
- 66. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Плюсы алгоритма Верле Несомненным достоинством данного алгоритма является
- 67. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Плюсы алгоритма Верле Несомненным достоинством данного алгоритма является
- 68. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Минусы алгоритма Верле скорости частиц напрямую не генерируются,
- 69. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Минусы алгоритма Верле скорости частиц напрямую не генерируются,
- 70. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. Минусы алгоритма Верле скорости частиц напрямую не генерируются,
- 71. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. атомные позиции определяются из двух предыдущих шагов по
- 72. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. В скоростном алгоритме Верле положения, скорости и ускорения
- 73. Основы метода молекулярной динамики Алгоритмы интегрирования уравнений движения. В скоростном алгоритме Верле положения, скорости и ускорения
- 74. Основы метода молекулярной динамики В статистической физике различаются 4 основных вида статистических ансамблей:
- 75. Основы метода молекулярной динамики В статистической физике различаются 4 основных вида статистических ансамблей: 1. Микроканонический ансамбль,
- 76. Основы метода молекулярной динамики В статистической физике различаются 4 основных вида статистических ансамблей: 1. Микроканонический ансамбль,
- 77. Основы метода молекулярной динамики В статистической физике различаются 4 основных вида статистических ансамблей: 1. Микроканонический ансамбль,
- 78. Основы метода молекулярной динамики В статистической физике различаются 4 основных вида статистических ансамблей: 1. Микроканонический ансамбль,
- 79. Основы метода молекулярной динамики Каждый ансамбль характеризуется набором заданных термодинамических величин (отраженных в названиях ансамблей) NVE-ансамбль
- 80. Основы метода молекулярной динамики Каждый ансамбль характеризуется набором заданных термодинамических величин (отраженных в названиях ансамблей) NVE-ансамбль
- 81. Основы метода молекулярной динамики Каждый ансамбль характеризуется набором заданных термодинамических величин (отраженных в названиях ансамблей) NVE-ансамбль
- 82. Основы метода молекулярной динамики Различают 4 основных способа поддержания постоянной термодинамической величины:
- 83. Основы метода молекулярной динамики Различают 4 основных способа поддержания постоянной термодинамической величины: Дифференциальный, когда величина имеет
- 84. Основы метода молекулярной динамики Различают 4 основных способа поддержания постоянной термодинамической величины: Дифференциальный, когда величина имеет
- 85. Основы метода молекулярной динамики Различают 4 основных способа поддержания постоянной термодинамической величины: Интегральный, когда гамильтониан системы
- 86. Основы метода молекулярной динамики Различают 4 основных способа поддержания постоянной термодинамической величины: Интегральный, когда гамильтониан системы
- 87. Основы метода молекулярной динамики Методы интегрирования уравнений движения обеспечивают сохранение энергии системы. Объем расчетной ячейки и
- 88. Основы метода молекулярной динамики Методы интегрирования уравнений движения обеспечивают сохранение энергии системы. Объем расчетной ячейки и
- 89. Основы метода молекулярной динамики Методы интегрирования уравнений движения обеспечивают сохранение энергии системы. Объем расчетной ячейки и
- 90. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Что означает “постоянная температура” ?
- 91. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Что означает “постоянная температура” ? Температуру некоторой
- 92. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Что означает “постоянная температура” ? Температуру некоторой
- 93. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. При таком распределении между средней кинетической энергией
- 94. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. При таком распределении между средней кинетической энергией
- 95. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. При таком распределении между средней кинетической энергией
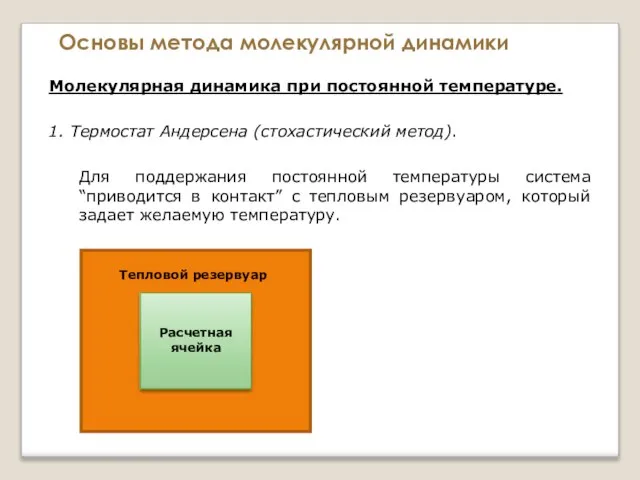
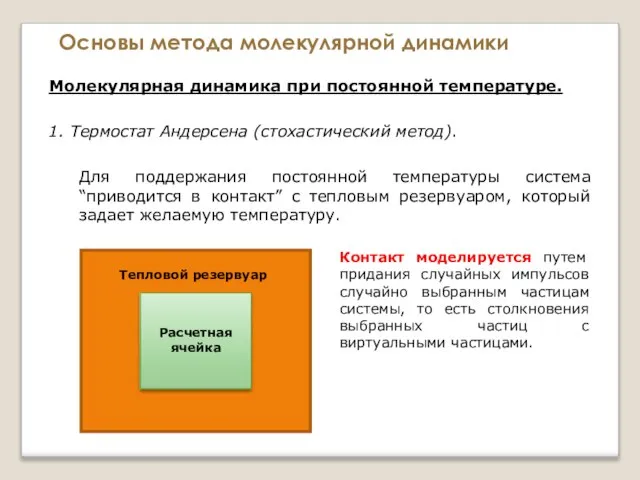
- 96. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. 1. Термостат Андерсена (стохастический метод).
- 97. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. 1. Термостат Андерсена (стохастический метод). Для поддержания
- 98. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. 1. Термостат Андерсена (стохастический метод). Для поддержания
- 99. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. 1. Термостат Андерсена (стохастический метод). Для поддержания
- 100. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. 1. Термостат Андерсена (стохастический метод). Для поддержания
- 101. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Алгоритмическая реализация термостата Андерсена:
- 102. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Алгоритмическая реализация термостата Андерсена: 1. Начиная с
- 103. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Алгоритмическая реализация термостата Андерсена: 1. Начиная с
- 104. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Алгоритмическая реализация термостата Андерсена: 1. Начиная с
- 105. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Алгоритмическая реализация термостата Андерсена: 1. Начиная с
- 106. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Алгоритмическая реализация термостата Андерсена: 1. Начиная с
- 107. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. 2. Метод расширенной системы, или интегральный метод.
- 108. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Метод ограничивающих условий, или дифференциальный термостат. Один
- 109. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Метод ограничивающих условий, или дифференциальный термостат. 1.
- 110. Основы метода молекулярной динамики Молекулярная динамика при постоянной температуре. Пропорциональный термостат – термостат Берендсена. Пропорциональный термостат
- 111. Основы метода молекулярной динамики Молекулярная динамика при постоянном давлении. Алгоритмы поддержания постоянного давления часто называются «баростатами».
- 112. Основы метода молекулярной динамики Молекулярная динамика при постоянном давлении. Алгоритмы поддержания постоянного давления часто называются «баростатами».
- 113. Основы метода молекулярной динамики Молекулярная динамика при постоянном давлении. Алгоритмы поддержания постоянного давления часто называются «баростатами».
- 115. Скачать презентацию







































































































 Обобщение знаний об основных классах неорганических соединений
Обобщение знаний об основных классах неорганических соединений X-Ray Diffraction in Biology (XRD). Физический принцип кристаллографии
X-Ray Diffraction in Biology (XRD). Физический принцип кристаллографии Натуральный каучук
Натуральный каучук Алкены
Алкены Ароматические углеводороды
Ароматические углеводороды Презентация на тему Хлор
Презентация на тему Хлор  Соединения Ca и Mg, представителей элементов II группы главной подгруппы
Соединения Ca и Mg, представителей элементов II группы главной подгруппы Любовь и химия
Любовь и химия Презентация на тему Занимательная химия
Презентация на тему Занимательная химия  Ароматические вещества и их значение для человека
Ароматические вещества и их значение для человека Взаимодействие атомов элементов-неметаллов между собой
Взаимодействие атомов элементов-неметаллов между собой Водород. Вода
Водород. Вода Технология растворов на неводных растворителях
Технология растворов на неводных растворителях Общие химические свойства металлов
Общие химические свойства металлов Металлургия
Металлургия Амины и анилин
Амины и анилин Сущность химических реакций и признаки их протекания
Сущность химических реакций и признаки их протекания Свойства химической связи
Свойства химической связи Углеводы. Глюкоза. 10 класс
Углеводы. Глюкоза. 10 класс Применение углерода
Применение углерода علاوي الندوة
علاوي الندوة Альдегиды
Альдегиды Кислоты. Кислоты, вокруг нас
Кислоты. Кислоты, вокруг нас Изменения, происходящие с веществами. Физические явления в химии
Изменения, происходящие с веществами. Физические явления в химии Натуральные и синтетические каучуки
Натуральные и синтетические каучуки Физико-химия поверхностных явлений в функционировании живых систем
Физико-химия поверхностных явлений в функционировании живых систем Презентация на тему Химические волокна
Презентация на тему Химические волокна  Внеклассное мероприятие по химии. Своя игра
Внеклассное мероприятие по химии. Своя игра