11u-2_Моделирование

Моделирование
§ 6. Модели и моделирование

Модели и моделирование
Модель – это объект, который обладает существенными свойствами другого объекта, процесса или явления (оригинала) и используется вместо него.
Моделирование – это создание и исследование моделей с целью изучения оригиналов.
Задачи моделирования:
исследование оригинала
анализ («что будет, если …»)
синтез («как сделать, чтобы …»)
оптимизация («как сделать лучше всего …»)

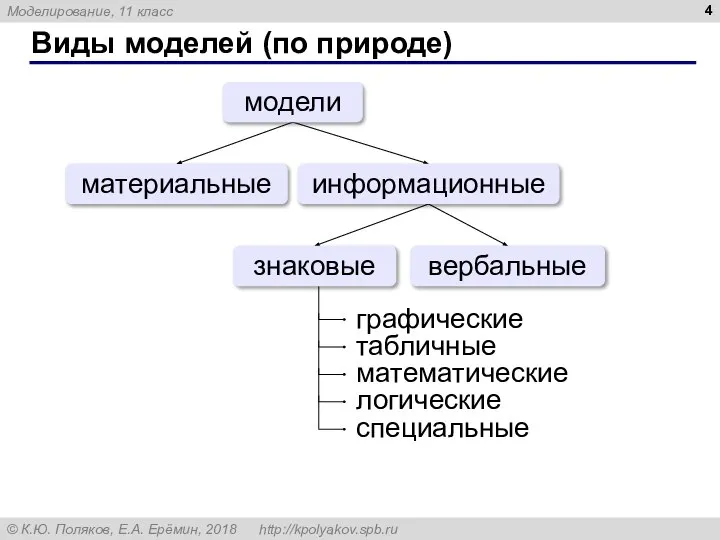
Виды моделей (по природе)
материальные
вербальные
модели
знаковые
информационные

Виды моделей (по фактору времени)
статические – описывают оригинал в заданный момент времени
силы, действующие на тело в состоянии покоя
результаты осмотра врача
фотография
динамические
модель движения тела
явления природы (молния, землетрясение, цунами)
история болезни
видеозапись события
…
дискретные модели описывают поведение только в отдельные моменты времени
непрерывные модели – в любой момент времени

Виды моделей (по характеру связей)
детерминированные – при одинаковых исходных данных всегда получается тот же результат
расчёт по формулам
движение корабля на спокойной воде
…
вероятностные – учитывают случайность событий
броуновское движение частиц
полета самолёта с учетом ветра
движения корабля на волнении
поведение человека
…

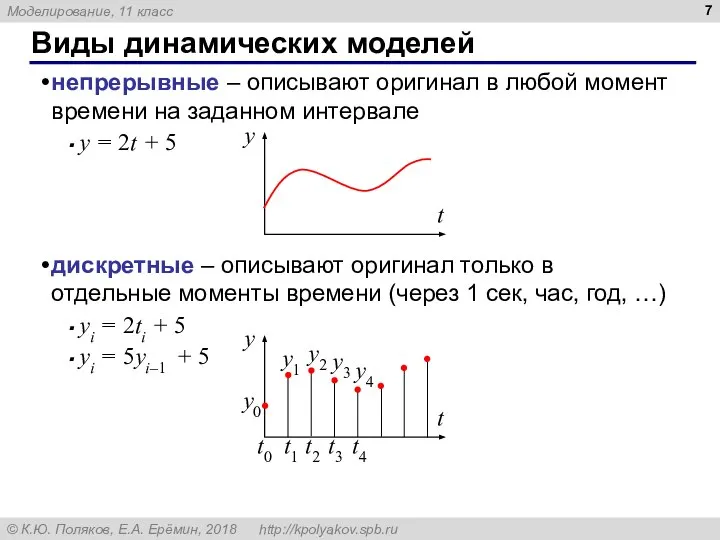
Виды динамических моделей
непрерывные – описывают оригинал в любой момент времени на заданном интервале
y = 2t + 5
дискретные – описывают оригинал только в отдельные моменты времени (через 1 сек, час, год, …)
yi = 2ti + 5
yi = 5yi–1 + 5

Имитационные модели
нельзя заранее вычислить или предсказать поведение системы, но можно имитировать её реакцию на внешние воздействия
максимальный учет всех факторов
только численные результаты
Примеры:
испытания лекарств на мышах, обезьянах, …
математическое моделирование биологических систем
модели систем массового обслуживания
модели процесса обучения
кросс-программирование
…

Игровые модели
экономические ситуации
военные действия
спортивные игры
тренинги персонала
Игровые модели учитывают действия противников.

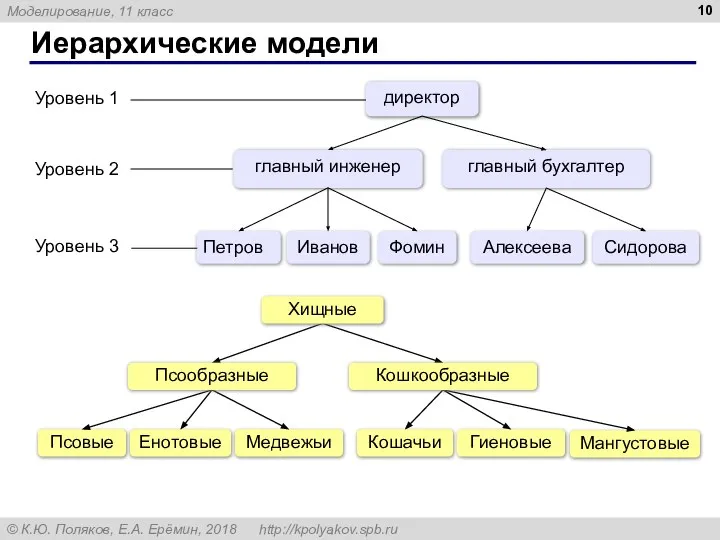
Иерархические модели

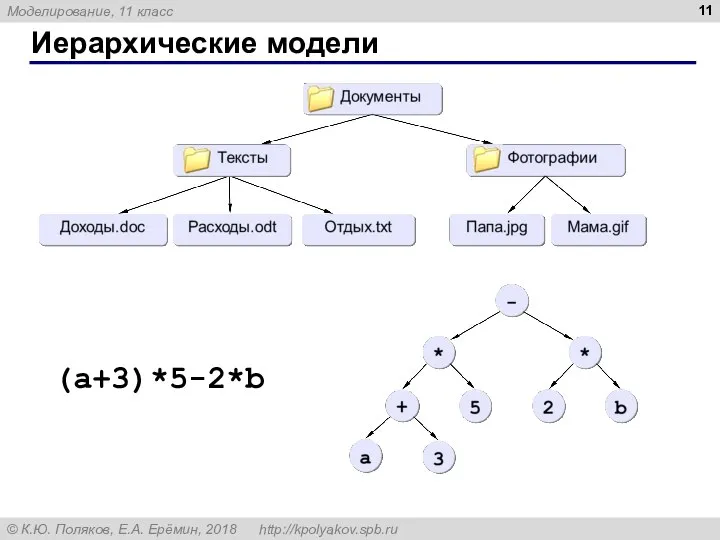
Иерархические модели
(a+3)*5-2*b

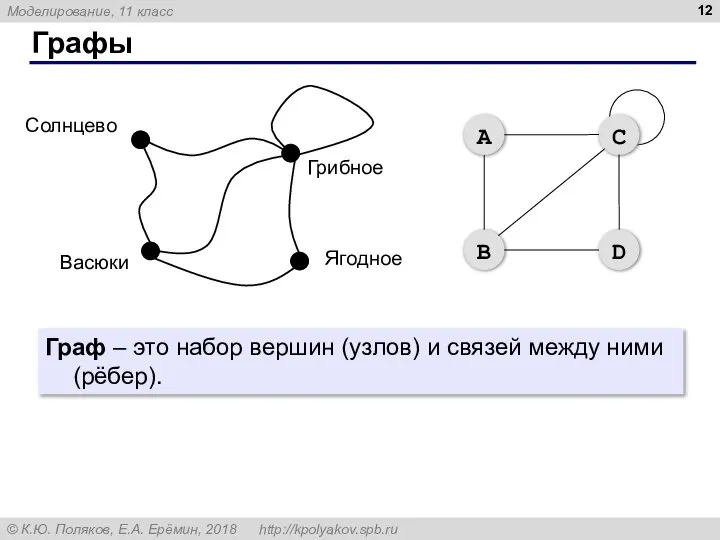
Графы
Граф – это набор вершин (узлов) и связей между ними (рёбер).

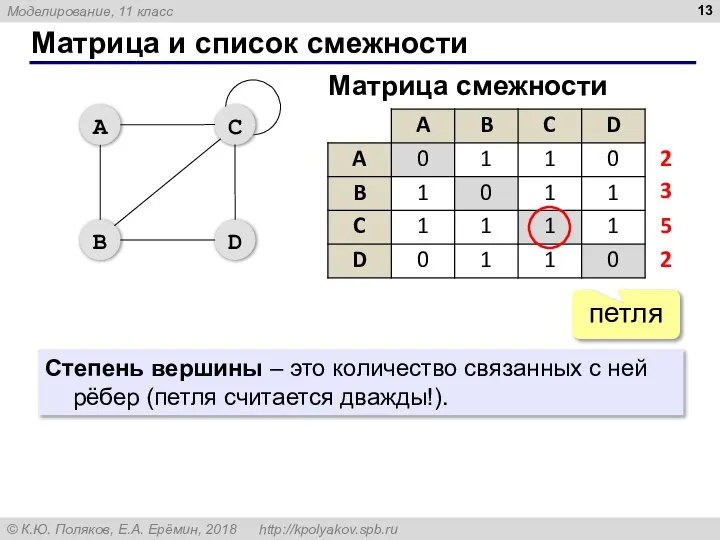
Матрица и список смежности
петля
Матрица смежности
Степень вершины – это количество связанных с ней рёбер (петля считается дважды!).
2
3
5
2

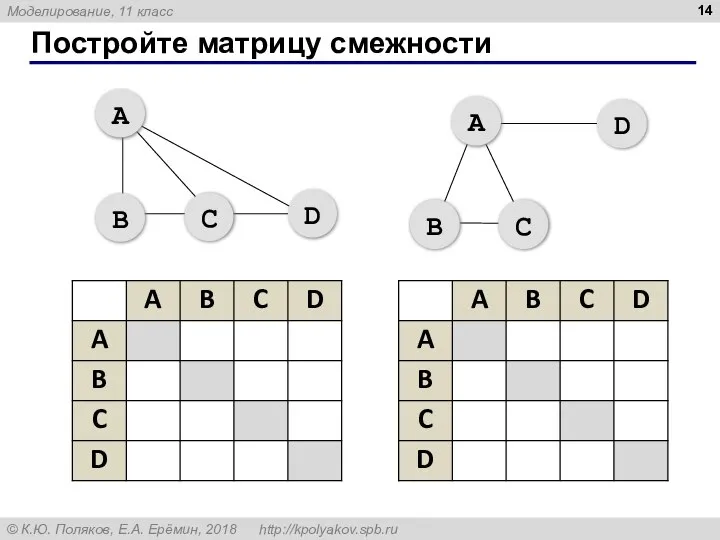
Постройте матрицу смежности

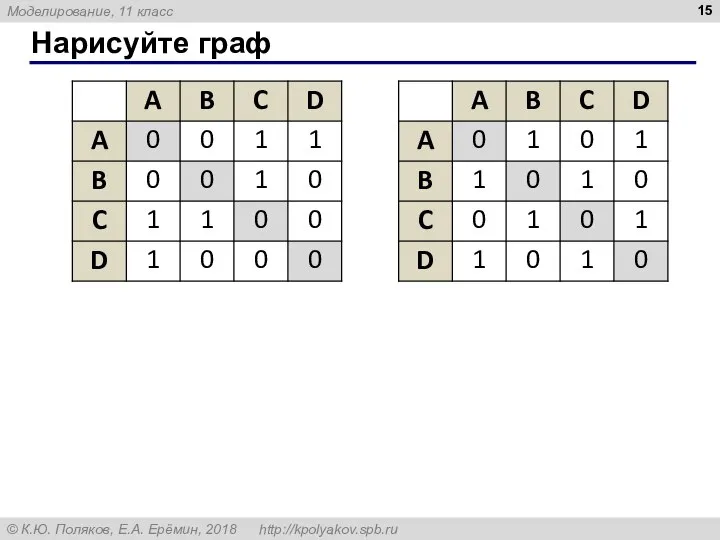
Нарисуйте граф

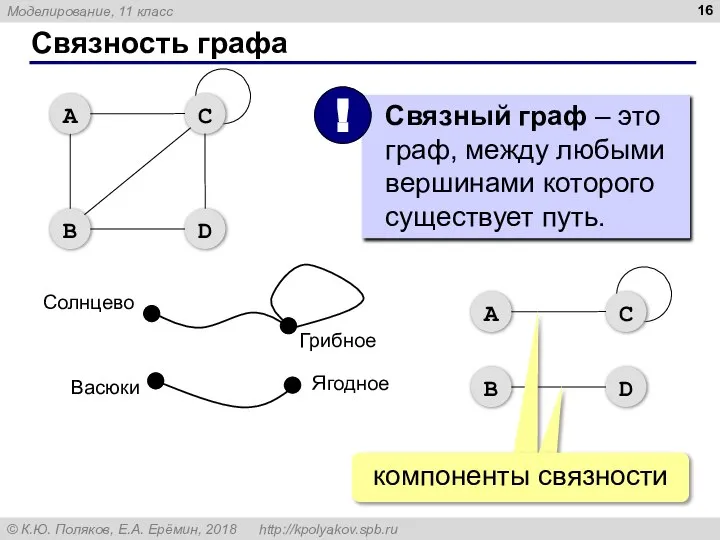
Связность графа

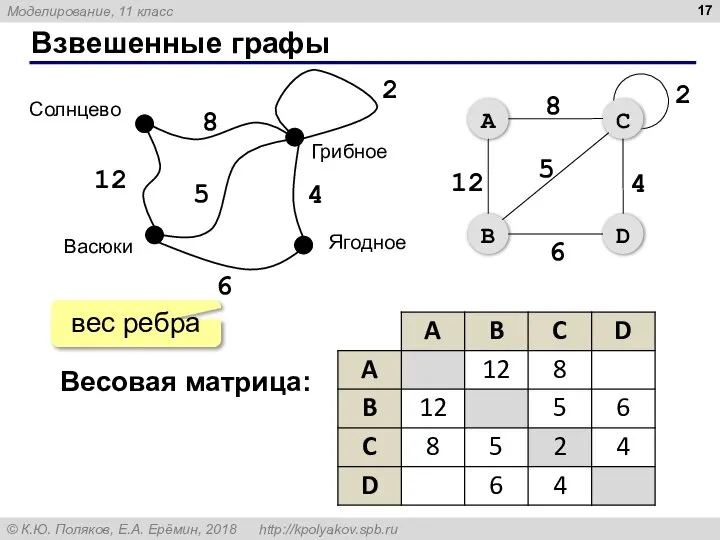
Взвешенные графы
12
8
2
5
4
6
Весовая матрица:
вес ребра

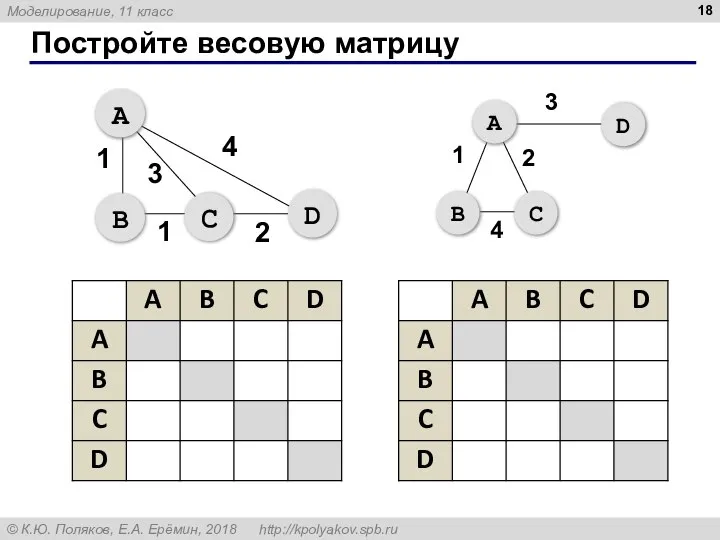
Постройте весовую матрицу

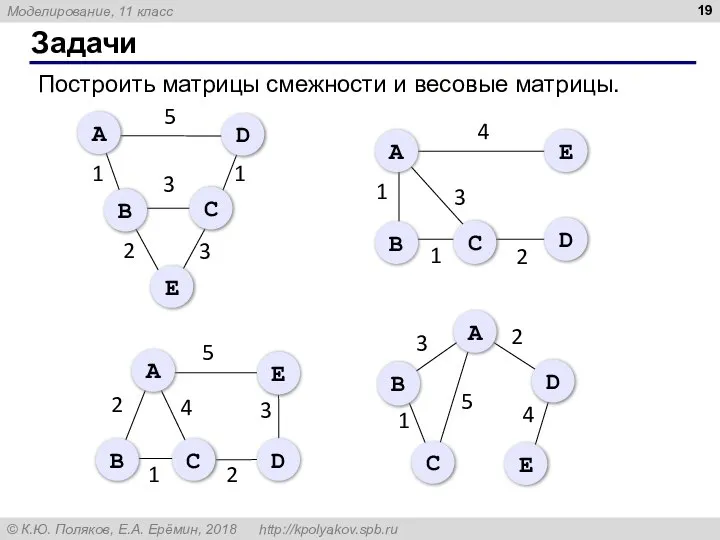
Задачи
Построить матрицы смежности и весовые матрицы.

Адекватность
Адекватность – это совпадение существенных свойств модели и оригинала в данной задаче.
Модель всегда отличается от оригинала
результаты моделирования согласуются с выводами теории (законы сохранения и т.п.)
… подтверждаются экспериментом (±10%)

Моделирование
§ 7. Игровые модели

Игровые стратегии
Задача: найти стратегию (алгоритм игры), который позволит получить лучший результат, если соперники играют безошибочно.
Игры с полной информацией: можно определить, кто должен выиграть, по начальной позиции.
Позиции:
проигрышные – все возможные ходы ведут в выигрышные позиции
выигрышные – хотя бы один ход ведёт в проигрышную позицию

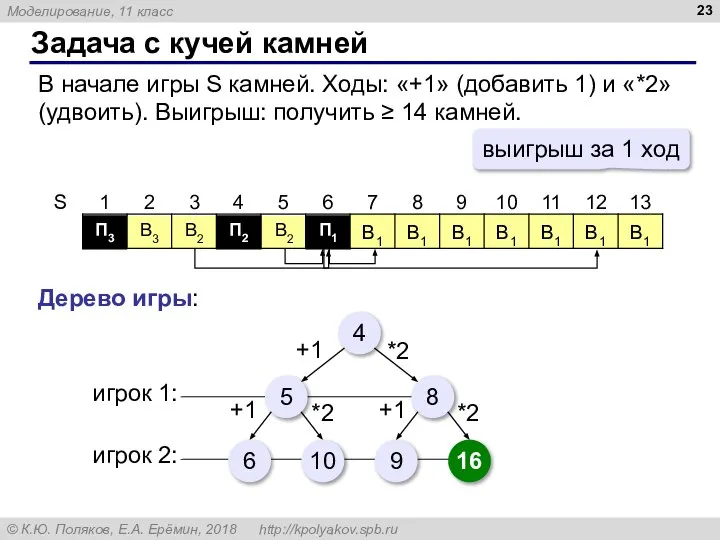
В2
П1
В2
П2
П3
В3
Задача с кучей камней
В начале игры S камней. Ходы: «+1» (добавить 1) и «*2» (удвоить). Выигрыш: получить ≥ 14 камней.
выигрыш за 1 ход
Дерево игры:
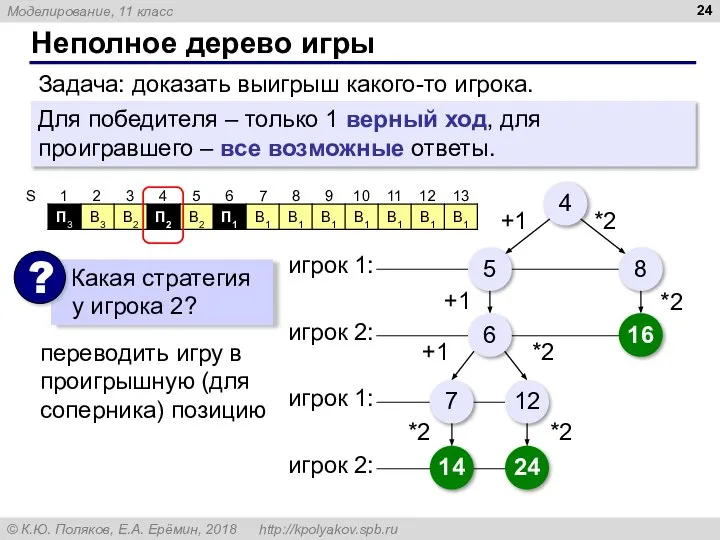
4

Неполное дерево игры
Задача: доказать выигрыш какого-то игрока.
Для победителя – только 1 верный ход, для проигравшего – все возможные ответы.
переводить игру в проигрышную (для соперника) позицию

Задачи
В начале игры S камней. Ходы: «+2» (добавить 2) и «*2» (удвоить). Выигрыш: получить ≥ 25 камней.
Построить дерево игры для S = 7.
В начале игры S камней. Ходы: «+1» (добавить 1) и «*3» (утроить). Выигрыш: получить ≥ 55 камней.
Построить дерево игры для S = 16.
В начале игры S камней. Ходы: «+2» (добавить 2), «+3» (добавить 3) и «*2» (удвоить). Выигрыш: получить ≥ 30 камней.
Построить дерево игры для S = 9.
Игра Баше. В начале игры S (S ≤ 15) камней. Ходы:
«-1» (взять 1), «-2» (взять 2) и «-3» (взять 3). Проигрыш: взять последний камень.
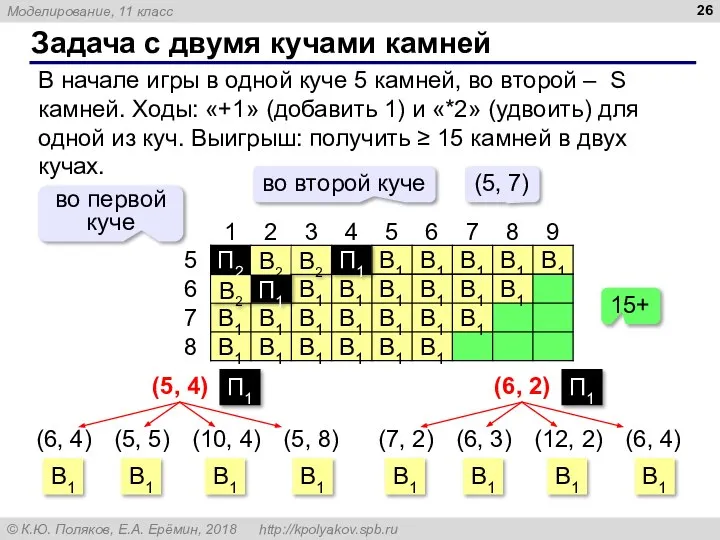
Построить дерево игры для S = 12.

Задача с двумя кучами камней
В начале игры в одной куче 5 камней, во второй – S камней. Ходы: «+1» (добавить 1) и «*2» (удвоить) для одной из куч. Выигрыш: получить ≥ 15 камней в двух кучах.
во второй куче
во первой куче
(5, 7)
15+
?
(5, 4)
(6, 4)
(5, 5)
(10, 4)
(5, 8)
B1
B1
B1
B1
П1
П1
?
П1
П2
В2
В2
В2
(6, 2)
П1

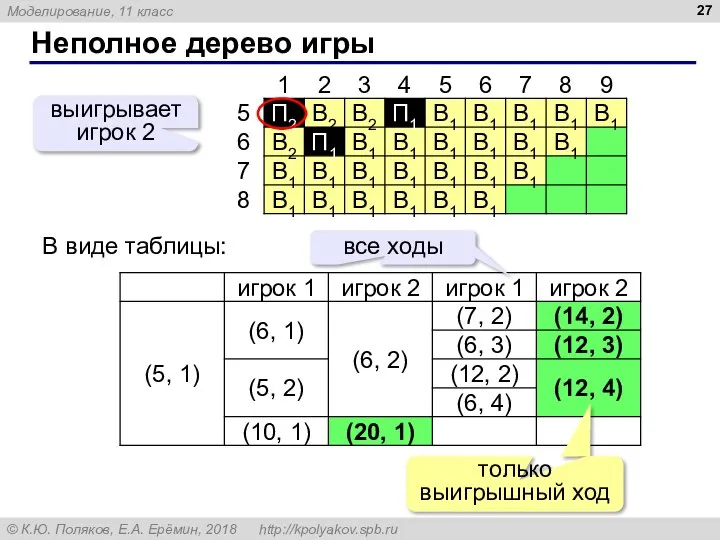
Неполное дерево игры
выигрывает игрок 2
В виде таблицы:

Моделирование
§ 8. Модели мышления

Искусственный интеллект
Задача: моделирование мышления человека для решения сложных задач, которые не удаётся решить алгоритмически.
экспертные системы
моделируют ход рассуждений человека-эксперта при принятии решений в сложных ситуациях:
ЕСЛИ у человека повышенная температура
ТО он нездоров
дедукция: от общих принципов к конкретному случаю
нейрокомпьютеры (нейросети)
поиск алгоритмов решения на основе анализа многих частных случаев (обучение)
индукция: от конкретных случаев к общему правилу

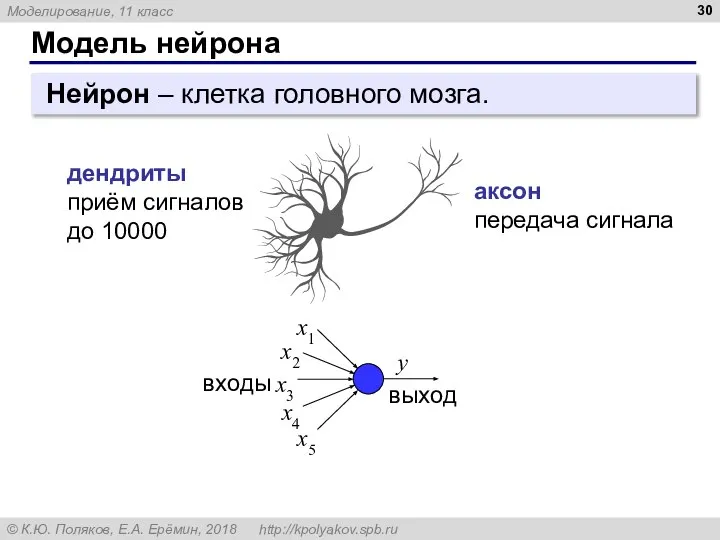
Модель нейрона
дендриты
приём сигналов
до 10000
аксон
передача сигнала
Нейрон – клетка головного мозга.

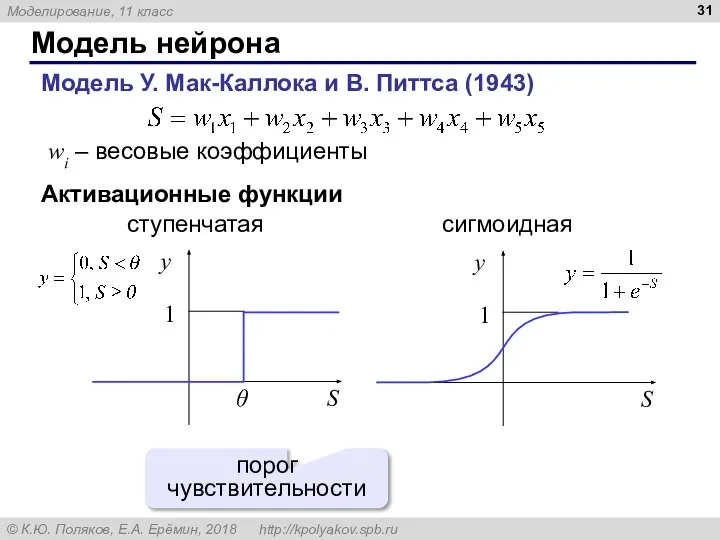
Модель нейрона
Модель У. Мак-Каллока и В. Питтса (1943)
wi – весовые коэффициенты
Активационные функции
ступенчатая
сигмоидная
порог чувствительности

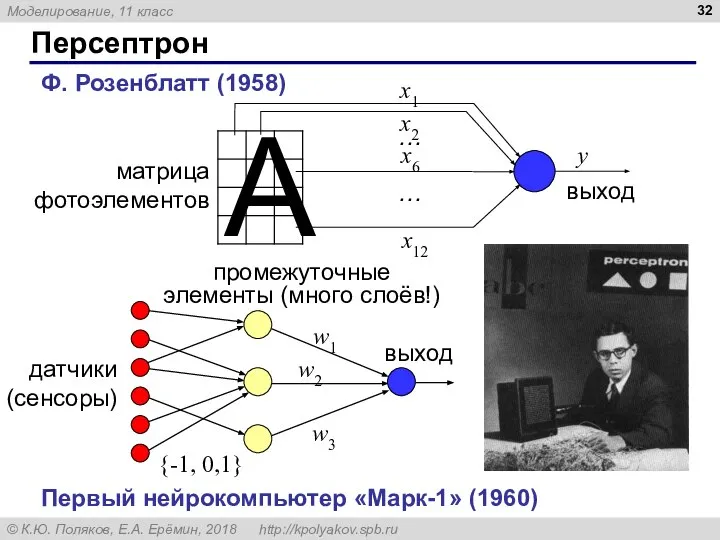
Персептрон
Ф. Розенблатт (1958)
Первый нейрокомпьютер «Марк-1» (1960)

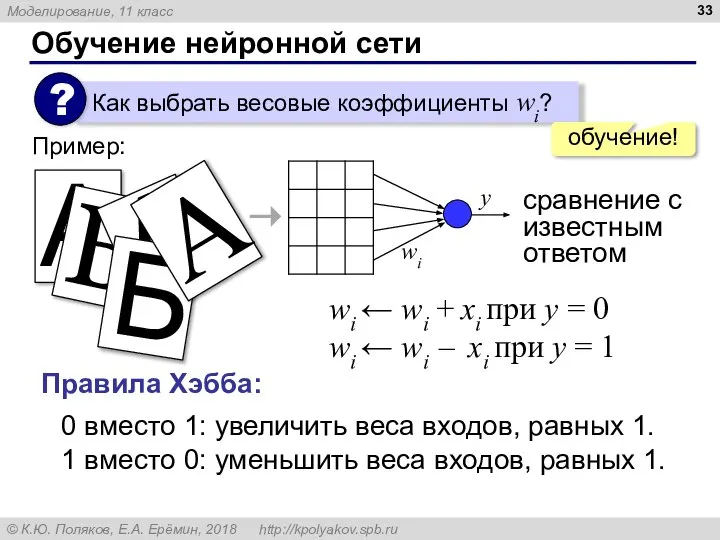
Обучение нейронной сети
обучение!
Пример:
0 вместо 1: увеличить веса входов, равных 1.
1 вместо 0: уменьшить веса входов, равных 1.
Правила Хэбба:
сравнение с
известным
ответом
wi ← wi + xi при y = 0
wi ← wi – xi при y = 1

Применение нейронных сетей
много примеров, но нет теории (алгоритма)
распознавание (лиц, голосов, отпечатков пальцев)
классификация (платёжеспособность клиента, проверка подлинности подписи, постановка диагноза)
прогнозирование (курсов валют, цен на сырьё)
МЧС РФ

Раскрашивание фотографий
чёрно-белое фото
это сделала нейронная сеть
цветное фото
color.artlebedev.ru

Интеллектуальные игры
игра «го»
Ли Седоль
Google DeepMind
1:4

Беспилотные автомобили

Нейронные сети: итоги
могут работать при неопределенности данных, в условиях помех
обрабатывают информацию параллельно
способны самообучаться
не используют и не выявляют законы природы
не могут объяснить результат

Машинное обучение
Machine Learning
Задача машинного обучения – разработка автоматических методов анализа данных и извлечения из них каких-то закономерностей.

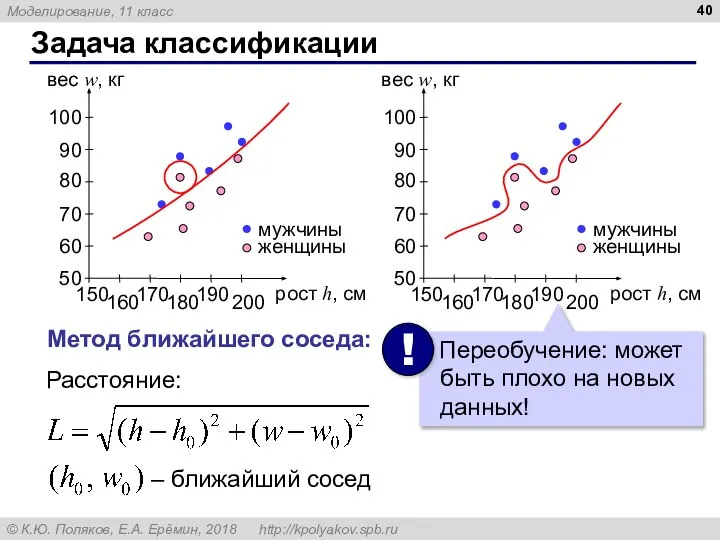
Задача классификации
Метод ближайшего соседа:

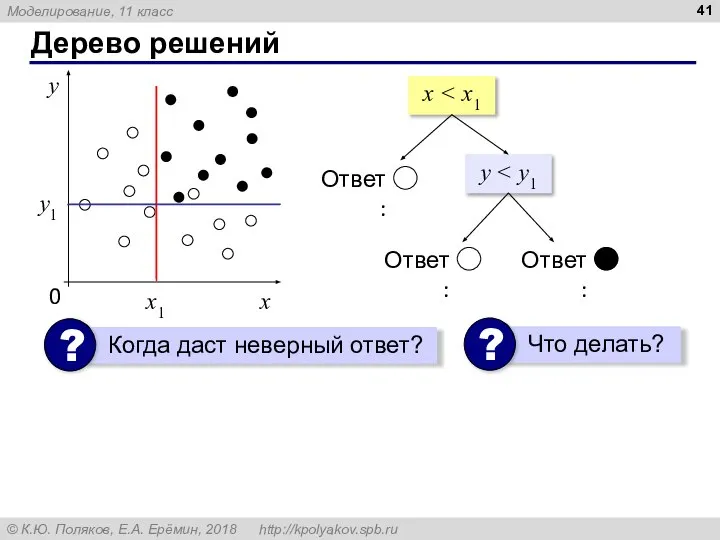
Дерево решений

Применение машинного обучения
классификация
распознавания образов
предсказание
анализ текстов
машинный перевод
ранжирование страниц в поисковых системах
рекомендации (музыка, реклама)

Большие данные (Big Data)
имеют очень большой объём (терабайты и петабайты);
не могут храниться и обрабатываться на одном компьютере.
Часто такие данные
поступают с большой скоростью (мегабайты и гигагабайты в секунду)
очень разнообразны (числа, графика, видео)
Серверы Google: > 24 Пбайт в день
Решение:
распределённые базы данных
кластеры для параллельной обработки

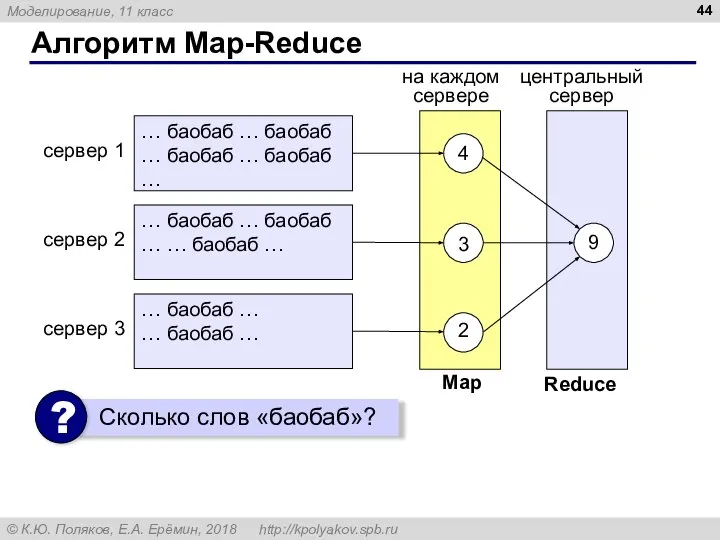
Алгоритм Map-Reduce
… баобаб … баобаб … баобаб … баобаб …
… баобаб … баобаб … … баобаб …
… баобаб …
… баобаб …
сервер 1
сервер 2
сервер 3

Моделирование
§ 9. Этапы моделирования

I. Постановка задачи
исследование оригинала
изучение сущности объекта или явления
анализ («что будет, если …»)
научиться прогнозировать последствий при различных воздействиях на оригинал
синтез («как сделать, чтобы …»)
научиться управлять оригиналом, оказывая на него воздействия
оптимизация («как сделать лучше»)
выбор наилучшего решения в заданных условиях

I. Постановка задачи
Хорошо поставленная задача:
описаны все связи между исходными данными и результатом
известны все исходные данные
решение существует
задача имеет единственное решение
Примеры плохо поставленных задач:
Уроки в школе начинаются в 830. В 1000 к школе подъехал красный автомобиль. Определите, когда Вася выйдет играть в футбол?
Вася бросает мяч со скоростью 12 м/с. Где мяч впервые ударится о землю?
Решить уравнение sin x = 4 (нет решений).
Найти функцию, которая проходит через точки (0,1) и (1,0) (бесконечно много решений).

I. Постановка задачи (пример)
Спортсмен Вася в синей кепке бросает белый мяч со скоростью 12 м/с. Под каким углом к горизонту ему нужно бросить мяч, чтобы попасть в желтую мишень?

II. Разработка модели
Спортсмен Вася в синей кепке бросает белый мяч со скоростью 12 м/с. Под каким углом к горизонту ему нужно бросить мяч, чтобы попасть в желтую мишень? Мишень расположена на высоте 4 м на расстоянии 10 м от Васи. В момент броска мяч находится на высоте 2 м от земли.
1) Определить существенные исходные данные.
мяч и мишень — материальные точки
мишень неподвижна
сопротивление воздуха не учитывается.
2) Выбор типа модели.

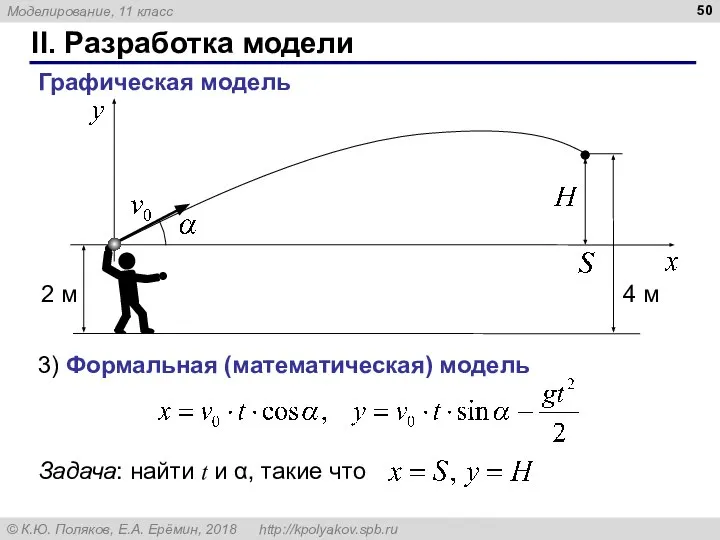
II. Разработка модели
Графическая модель
3) Формальная (математическая) модель
,

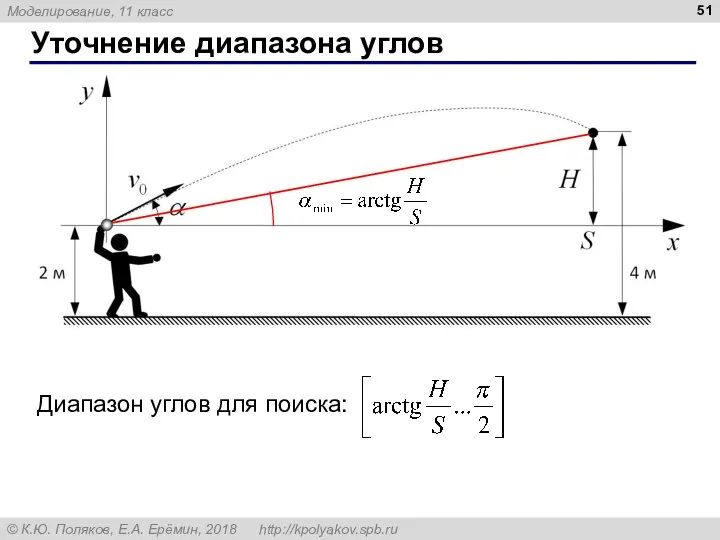
Уточнение диапазона углов
Диапазон углов для поиска:

II. Разработка модели
4) Алгоритм моделирования
Метод I.
Меняем угол α. Для выбранного угла α строим траекторию полета мяча. Если она проходит выше мишени, уменьшаем угол, если ниже – увеличиваем.
Метод II.
Из первого равенства выражаем время полета:
Меняем угол α. Для выбранного угла α считаем t, а затем – значение y при этом t. Если оно больше H, уменьшаем угол, если меньше – увеличиваем.
не надо строить всю траекторию для каждого α

II. Разработка модели
5) Компьютерная модель
программа (Паскаль, Си, …)
электронные таблицы (Excel, OpenOffice.org Calc)
среды моделирования (Simulink, VisSim)

III. Тестирование модели
Тестирование – это проверка модели на простых исходных данных с известным результатом.
а) тестирование математической модели:
• при t = 0 ⇒ x = 0, y = 0 (в начале координат)
• при v0 = 0 ⇒ x = 0, (падение вниз)
• при α = 90° ⇒ x = 0
• при увеличении t парабола «загибается» вниз
б) тестирование компьютерной модели:
(пробные расчёты в рассмотренных условиях)

IV. Эксперимент с моделью
Эксперимент – это исследование модели при тех исходных данных, которые нас интересуют (результат заранее неизвестен).
задаём угол α
находим время
находим высоту
построить график y(α)

V. Анализ результатов эксперимента
Возможные выводы:
задача решена, модель адекватна
необходимо изменить алгоритм или условия моделирования
необходимо изменить модель (учесть дополнительные свойства)
необходимо изменить постановку задачи

V. Анализ результатов
всегда ли Вася сможет попасть в мишень?
если начальная скорость отличается от заданной?
если мяч и мишень не считать материальными точками?
как сильно влияет сопротивление воздуха?
если мишень качается?
и т.д….

Моделирование
§ 10. Моделирование движения

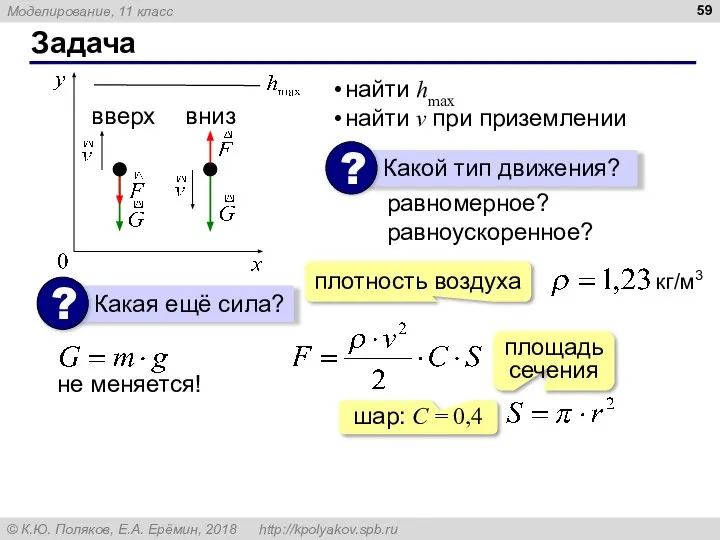
Задача
найти hmax
найти v при приземлении
плотность воздуха
площадь
сечения
шар: С = 0,4
равномерное?
равноускоренное?
не меняется!

Математическая модель
В проекции на ось OY:
всегда противоположна v
Методы решения:
аналитический (высшая математика)
численное моделирование

Дискретизация
Дискретная модель описывает состояние системы при
шаг дискретизации
Задача: зная (yi, vi, ai) при ti = i⋅δ
найти (yi+1, vi+1, ai+1) при ti+1 = (i+1)⋅δ
Допущение: силы (и ускорение) не меняются
на интервале [ti, ti+1]
Вычисления:

Компьютерная модель
t:= 0; v:= v0; y:= 0
k:= ro*C*S/2
нц пока y >= 0 F:= - k*abs(v)*v | сила сопротивления
a:= - g + F/m | ускорение
y:= y + v*delta + a*delta*delta/2 | координата
v:= v + a*delta | скорость
t:= t + delta | время
кц
если y > h то
h:= y
все

Моделирование
§ 11. Математические модели в биологии

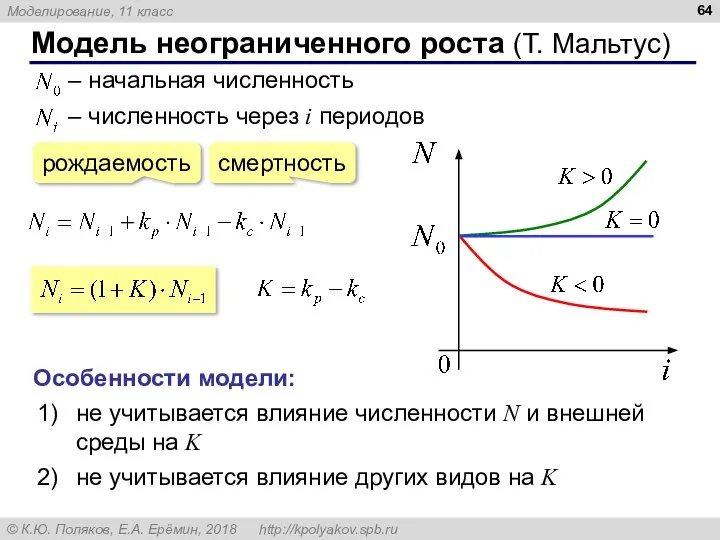
Модель неограниченного роста (Т. Мальтус)
Особенности модели:
не учитывается влияние численности N и внешней среды на K
не учитывается влияние других видов на K

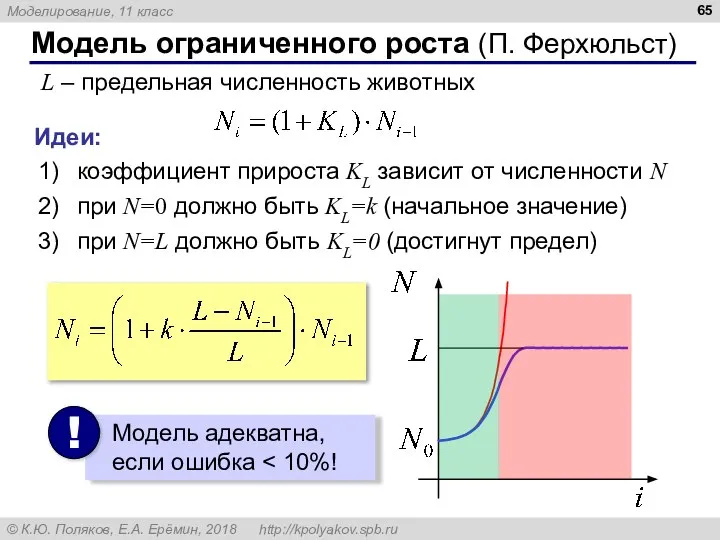
Модель ограниченного роста (П. Ферхюльст)
L – предельная численность животных
Идеи:
коэффициент прироста KL зависит от численности N
при N=0 должно быть KL=k (начальное значение)
при N=L должно быть KL=0 (достигнут предел)

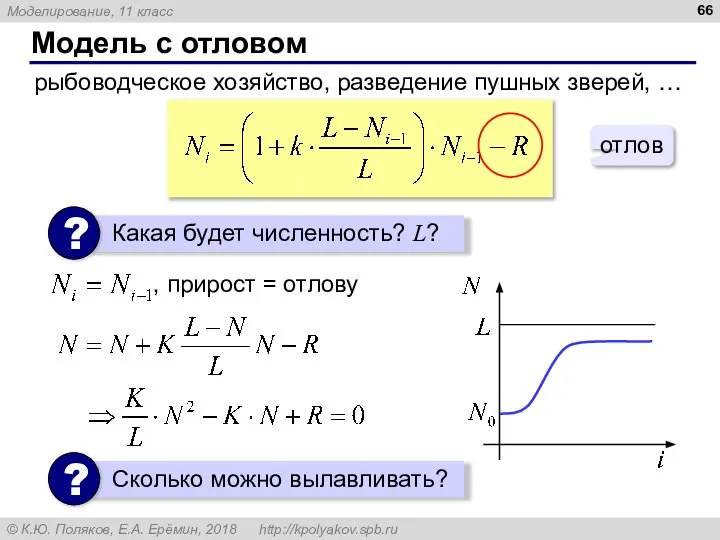
Модель с отловом
рыбоводческое хозяйство, разведение пушных зверей, …

Модель «хищник-жертва»
Модель – не-система:
Модель – система:
число встреч пропорционально Ni⋅Zi
«эффект» пропорционален числу встреч

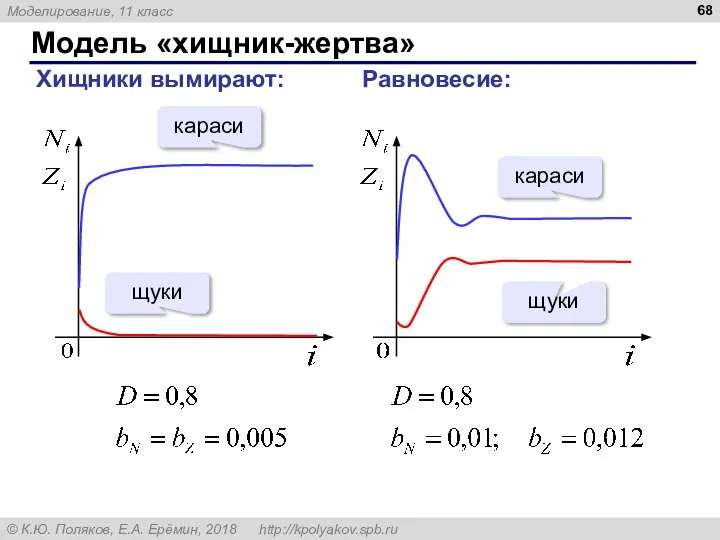
Модель «хищник-жертва»
Хищники вымирают:
Равновесие:
караси
щуки
караси
щуки

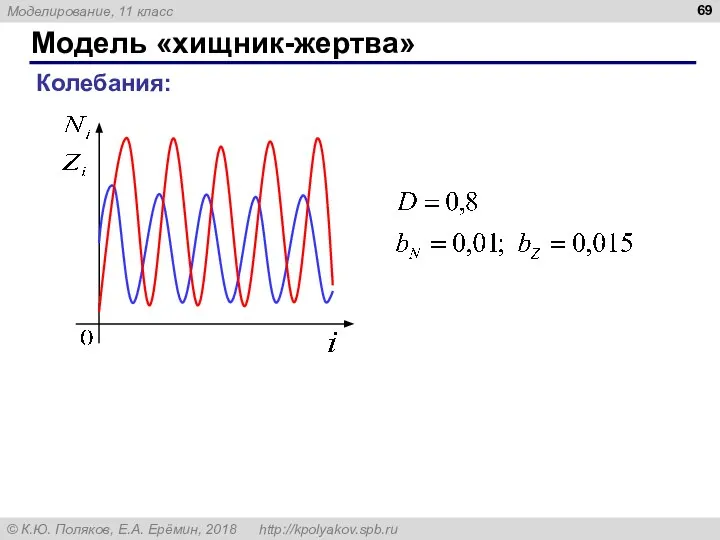
Модель «хищник-жертва»
Колебания:

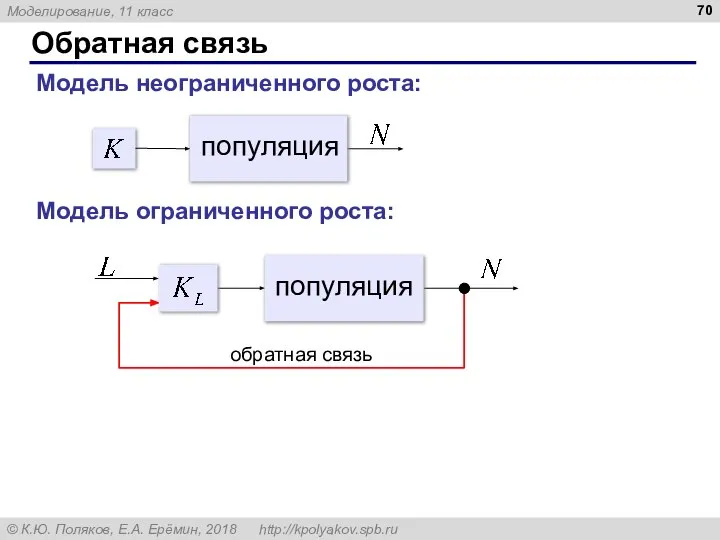
Обратная связь
Модель неограниченного роста:
Модель ограниченного роста:

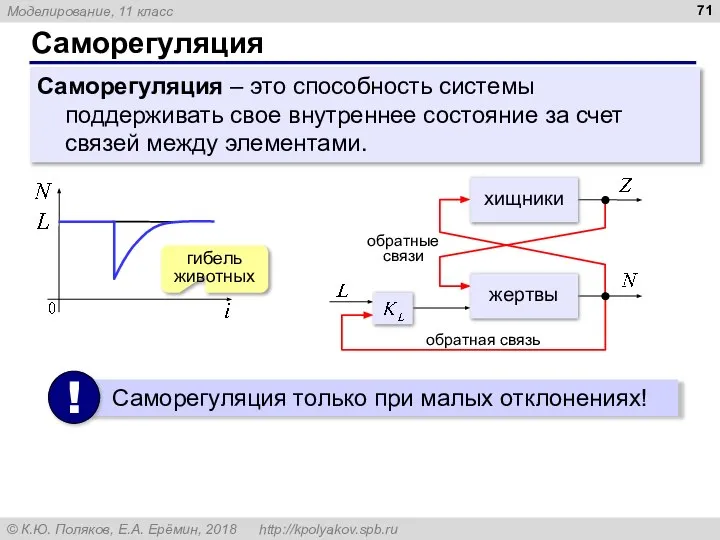
Саморегуляция
Саморегуляция – это способность системы поддерживать свое внутреннее состояние за счет связей между элементами.

Моделирование
§ 12. Вероятностные модели

Методы Монте-Карло
Методы Монте-Карло – это методы решения вычислительных задач с помощью математического моделирования, основанные на использовании случайных чисел.
результат приближённый
это лучше, чем никакой

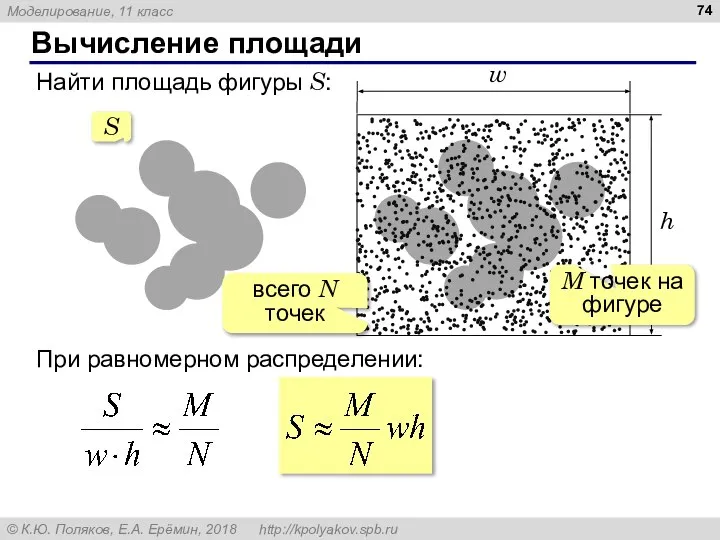
Вычисление площади
Найти площадь фигуры S:
всего N точек
M точек на фигуре
S
При равномерном распределении:

Вычисление числа π
цел i, M = 0, N = 100000
вещ x, y
нц для i от 1 до N
x := rand(0,1)
y := rand(0,1)
если x*x + y*y <= 1 то
M:= M + 1
все
кц
вывод "Pi = ", 4*M/N
если внутри круга

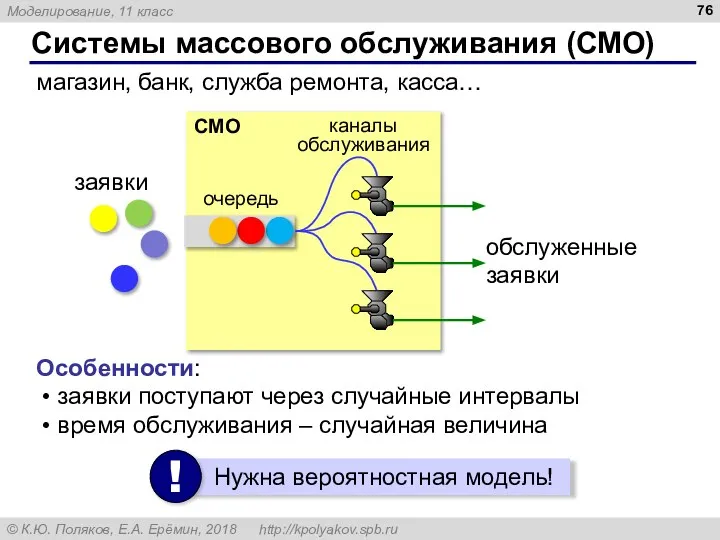
Системы массового обслуживания (СМО)
магазин, банк, служба ремонта, касса…
обслуженные
заявки
заявки поступают через случайные интервалы
время обслуживания – случайная величина
Особенности:

Модель работы банка
за 1 минуту входит P клиентов
время обслуживания T минут
K – количество касс
за 1 минуту входит от 0 до Pmax клиентов
время обслуживания от Tmin до Tmax минут
изменение числа клиентов в банке
средняя длина очереди
среднее время ожидания Qi⋅Ti
Допущение: распределение равномерное
Детерминированная модель:
Вероятностная модель:

Модель работы банка
K касс работают с одинаковой скоростью, но эта скорость меняется каждый интервал
Ti – случайное время обслуживания (от Tmin до Tmax)
обслужено за 1 интервал на 1 кассе 1/T,
на всех кассах
Задача: выбрать K так, чтобы среднее время ожидания было больше допустимого в течение не более 5% от полного времени моделирования.
Допущение:

Модель работы банка
K:= 2 | меняем количество касс
Pmax:= 4 | макс. число входящих за 1 мин
Tmin:= 1 | мин. время обслуживания
Tmax:= 9 | макс. время обслуживания
L:= 480 | период моделирования
M:= 15 | допустимое время ожидания
N:= 0 | сначала в банке никого нет
count:= 0 | счетчик «плохих» минут

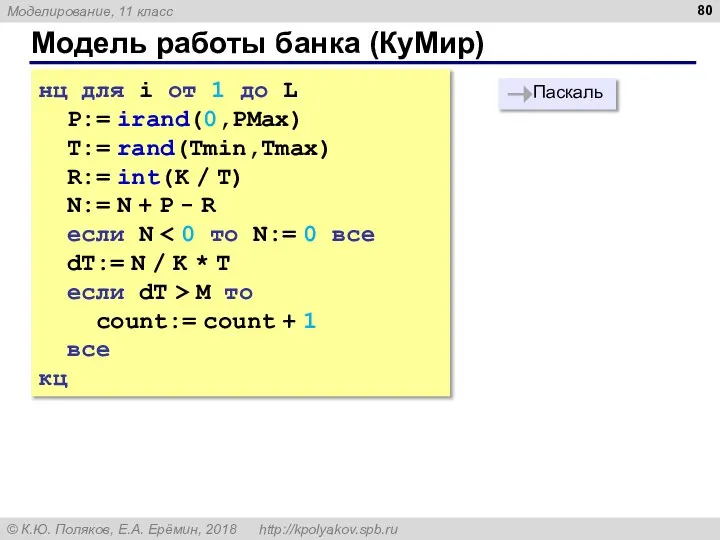
Модель работы банка (КуМир)
нц для i от 1 до L
P:= irand(0,PMax) T:= rand(Tmin,Tmax)
R:= int(K / T)
N:= N + P - R
если N < 0 то N:= 0 все
dT:= N / K * T
если dT > M то
count:= count + 1
все
кц

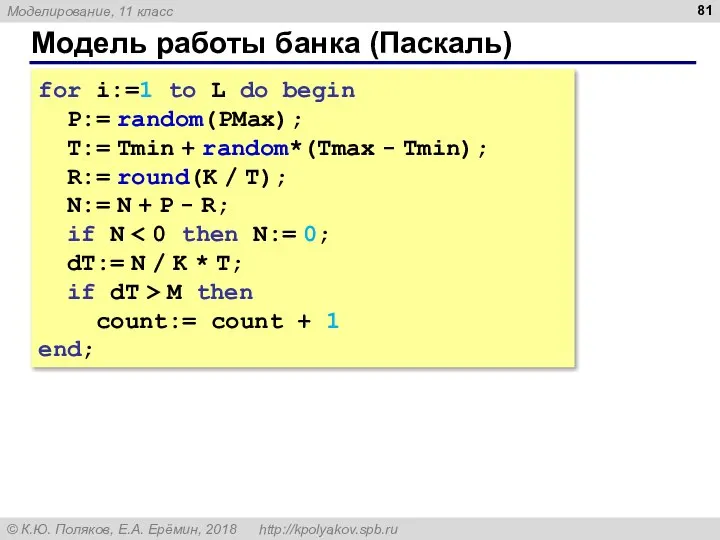
Модель работы банка (Паскаль)
for i:=1 to L do begin
P:= random(PMax);
T:= Tmin + random*(Tmax - Tmin);
R:= round(K / T);
N:= N + P - R;
if N < 0 then N:= 0;
dT:= N / K * T;
if dT > M then
count:= count + 1
end;

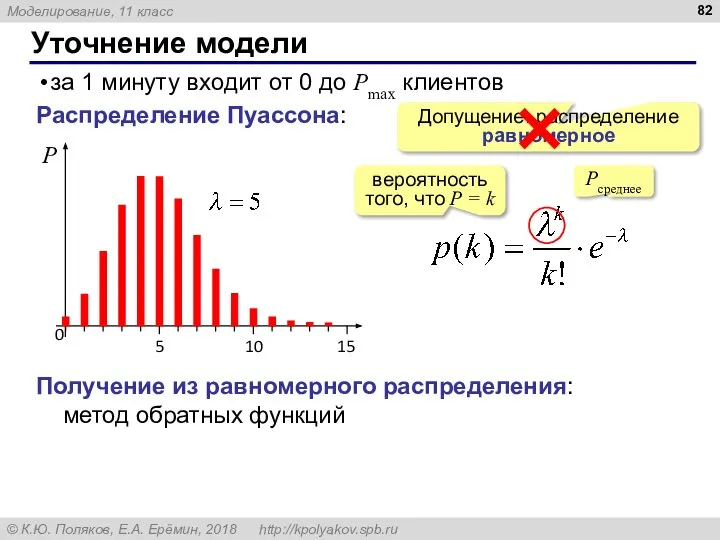
Уточнение модели
за 1 минуту входит от 0 до Pmax клиентов
Допущение: распределение равномерное
Распределение Пуассона:
вероятность того, что P = k
Pсреднее
Получение из равномерного распределения:
метод обратных функций

Распределение Пуассона (КуМир)
алг цел Poisson(цел Lam)
нач
вещ s, r, alpha;
цел k
r:= exp(-Lam); s:= r
k:= 0
alpha:= rand(0,1)
нц пока s < alpha
k:= k + 1
r:= r * Lam / k
s:= s + r
кц
знач:= k
кон

Распределение Пуассона (Паскаль)
function Poisson(Lam: integer): integer;
var s, r, alpha: real;
k: integer;
begin r:= exp(-Lam); s:= r;
k:= 0;
alpha:= random;
while s < alpha do begin
k:= k + 1;
r:= r * Lam / k;
s:= s + r
end;
Poisson:= k
end;

Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
[email protected]
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь
[email protected]