6 - Алгебра высказываний - ppt

ЛОГИКА
НАУКА О ФОРМАХ И СПОСОБАХ МЫШЛЕНИЯ

Джордж Буль – создатель алгебры логики
Джордж Буль – английский математик-самоучка
(1815-1864г)
Джордж Буль по праву считается отцом математической логики. Его именем назван раздел математической логики – булева алгебра.

Джордж Буль – создатель алгебры логики
Буль изобрел своеобразную алгебру - систему обозначений и правил, применимую ко всевозможным объектам, от чисел до предложений.
Пользуясь этой системой, он мог закодировать высказывания (утверждения, истинность или ложность которых требовалось доказать) с помощью символов своего языка, а затем манипулировать ими, подобно тому как в математике манипулируют числами. Основными операциями булевой алгебры являются конъюнкция (И), дизъюнкция (ИЛИ), отрицание (НЕ).

Применение алгебры логики для разработки ЭВМ
Через некоторое время стало понятно, что система Буля хорошо подходит для описания электрических переключателей схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому как утверждение может быть либо истинным, либо ложным.
А еще несколько десятилетий спустя, уже в ХХ столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.

Клод Шеннон связал алгебру логики с работой компьютера
Клод Шеннон
(1916-2001г) –
американский математик
В 1936 году выпускник Мичиганского университета Клод Шеннон, которому был тогда 21 год, сумел ликвидировать разрыв между алгебраической теорией логики и ее практическим приложением

Клод Шеннон связал алгебру логики с работой компьютера
Шеннон, имея два диплома бакалавра - по электротехнике и по математике, выполнял обязанности оператора на неуклюжем механическом вычислительном устройстве под названием "дифференциальный анализатор"
Постепенно у Шеннона стали вырисовываться контуры устройства компьютера. Если построить электрические цепи в соответствии с принципами булевой алгебры, то они могли бы выражать логические отношения, определять истинность утверждений, а также выполнять сложные вычисления.

Клод Шеннон связал алгебру логики с работой компьютера
Электрические схемы, очевидно, были бы гораздо удобнее шестеренок и валиков, щедро смазанных машинным маслом у "дифференциального анализатора".
Свои идеи относительно связи между двоичным исчислением, булевой алгеброй и электрическими схемами Шеннон развил в докторской диссертации, опубликованной в 1938 году.

Джон фон Нейман – создатель первой ЭВМ
Джон фон Нейман – американский математик
1903-1957

Удивительные способности Неймана
Джон фон Нейман родился в 1903 году в семье будапештского банкира и уже в восьмилетнем возрасте владел не только несколькими иностранными языками, но также знал основы высшей математики.
Он обладал феноменальной памятью и помнил все, что когда-либо слышал, видел или читал, мог дословно цитировать по памяти большие фрагменты книг, которые читал несколько лет назад.

Появление первых ЭВМ
В 1944 году фон Нейман был направлен в качестве консультанта по математическим вопросам в группу разработчиков первой ЭВМ ENIAC.
После окончания строительства ENIAC фон Нейман опубликовал отчет "Предварительное обсуждение логической конструкции электронной вычислительной машины". Этот отчет стал исходным пунктом в конструировании новых машин.
Сам Нейман занялся разработкой собственной версии вычислительной машины, которую назвал машиной с памятью с прямой адресацией - IAS (Immediate Address Storage).

Открытие фон Неймана
Уже во время работ над ENIAC фон Нейман понял, что создание компьютеров с большим количеством переключателей и проводов, которые реализуют тот или иной алгоритм, очень долго и утомительно.
И он понял: в памяти машины должны быть не только данные, которые обрабатываются в ходе работы, но также и сама программа.
Таким образом, его фундаментальным открытием в области вычислительной техники стала мысль, которая сегодня кажется нам такой естественной: в ходе работы компьютера и программа и обрабатываемые ею данные должны находиться в одном пространстве оперативной памяти.

Применение принципов алгебры логики для создания новой ЭВМ
В ходе строительства ENIAC Нейман пришел к выводу, что десятичная арифметика, реализуемая в ENIAC, очень неэффективна.
Для каждого десятичного разряда были отведены 10 ламп, и в любой момент времени горела только одна (скажем, если горит седьмая лампа, то в разряде стоит 7, если девятая - 9 и т. д.). В своей машине десятичную арифметику Нейман заменил двоичной.

«Фон-неймановская» машина
Все современные компьютеры в главных чертах повторяют архитектуру IAS (вычислительной машины, сконструированной фон Нейманом), которая в специальной литературе сегодня так и именуется - "архитектура фон Неймана", или "фон-неймановская машина".
Машина фон Неймана состояла из пяти основных узлов: памяти, арифметико-логического устройства (АЛУ), устройства управления и устройств ввода-вывода (в современных микропроцессорах АЛУ и устройство управления объединены в одном корпусе).

ВЫСКАЗЫВАНИЕ (суждение, утверждение)
повествовательное предложение, о котором можно однозначно сказать, что оно истинно или ложно
(Пример: Париж – столица Франции)

АЛГЕБРА ЛОГИКИ (высказываний)
наука об операциях над высказываниями

Понятия алгебры логики:
Логическая переменная – это простое высказывание, содержащее только одну мысль
Обозначение: латинская буква (А, В, Х …)
Значение: ИСТИНА (1) или ЛОЖЬ (0)
Логическая функция (или формула или логическое выражение)– это составное высказывание, которое содержит несколько простых высказываний, соединенных между собой с помощью логических операций
Обозначение: F
Логические операции – логическое действие (логическое умножение – коньюнкция, логическое сложение – дизъюнкция, отрицание – инверсия, следование – импликация, равенство – эквивалентность)

Объясните, почему следующие предложения не являются высказываниями:
а) Уходя гасите свет.
б) Какого цвета этот дом?
в) Посмотрите в окно.
2. Придумай 2 высказывания
3. Придумай сложное высказывание с союзом И

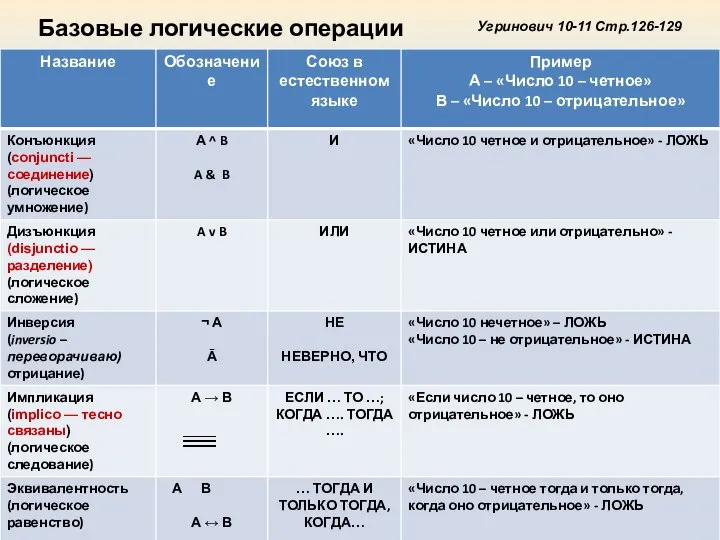
Базовые логические операции
Угринович 10-11 Стр.126-129

Таблица истинности
таблица определяющая значение сложного высказывания при всех возможных значениях простых высказываний

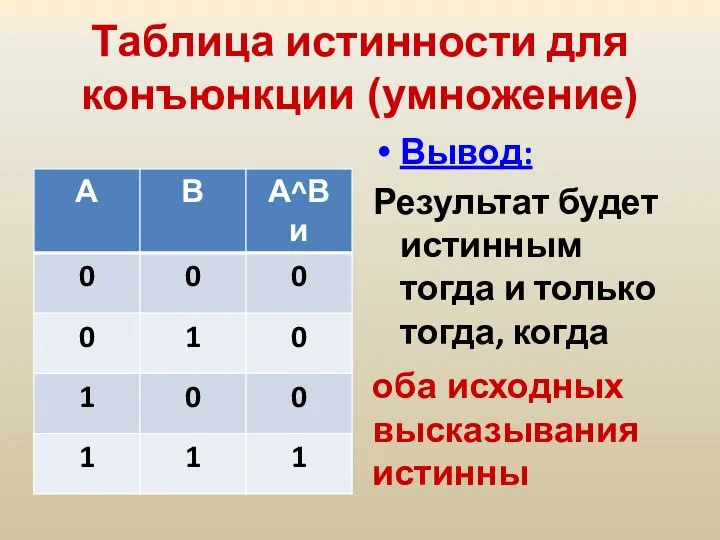
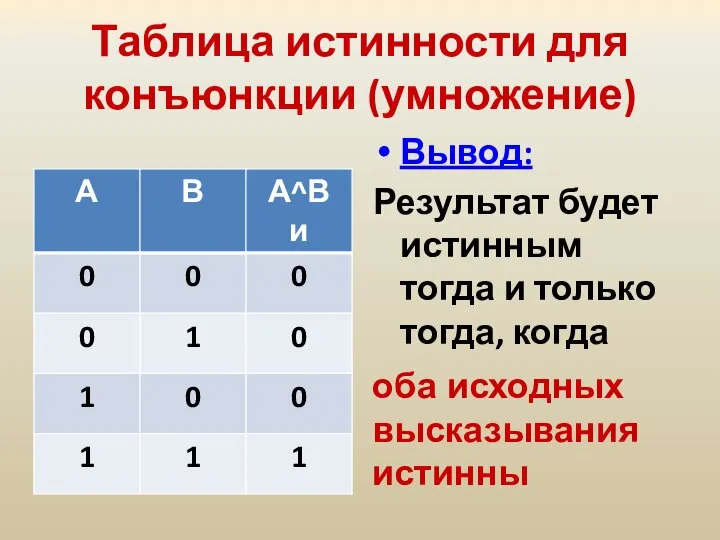
Таблица истинности для конъюнкции (умножение)
Вывод:
Результат будет истинным тогда и только тогда, когда
оба исходных высказывания истинны

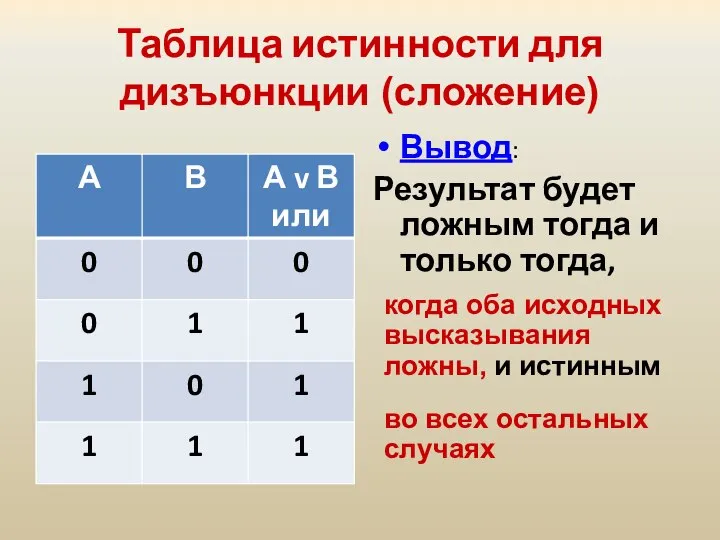
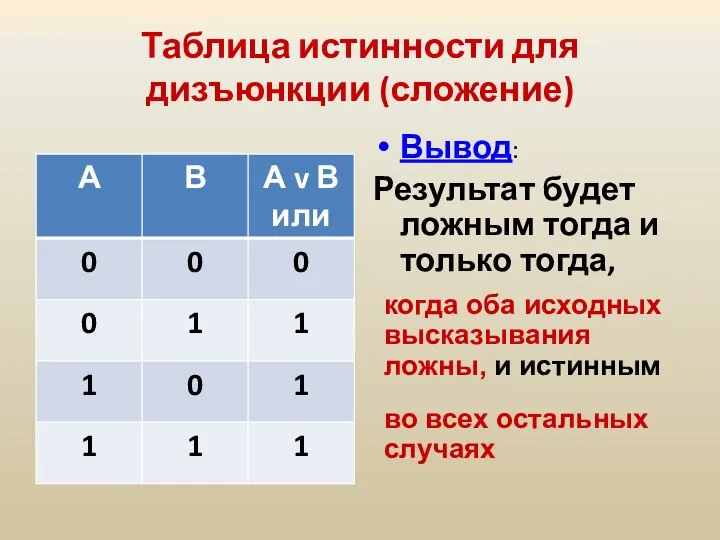
Таблица истинности для дизъюнкции (сложение)
Вывод:
Результат будет ложным тогда и только тогда,
когда оба исходных высказывания ложны, и истинным
во всех остальных случаях

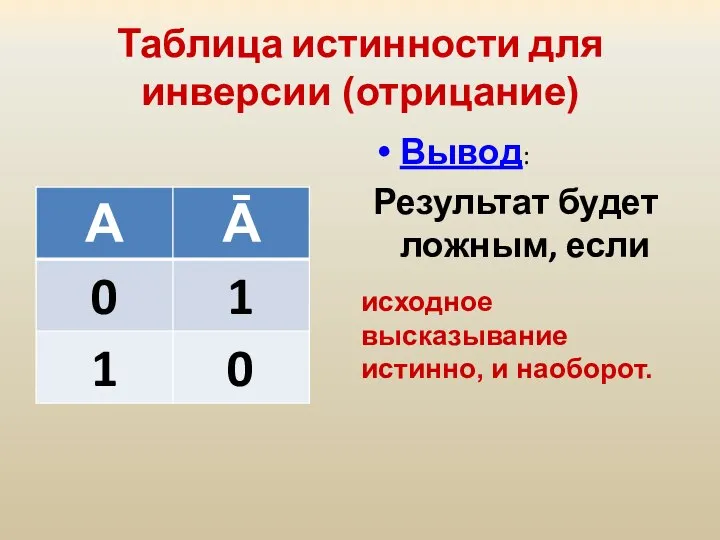
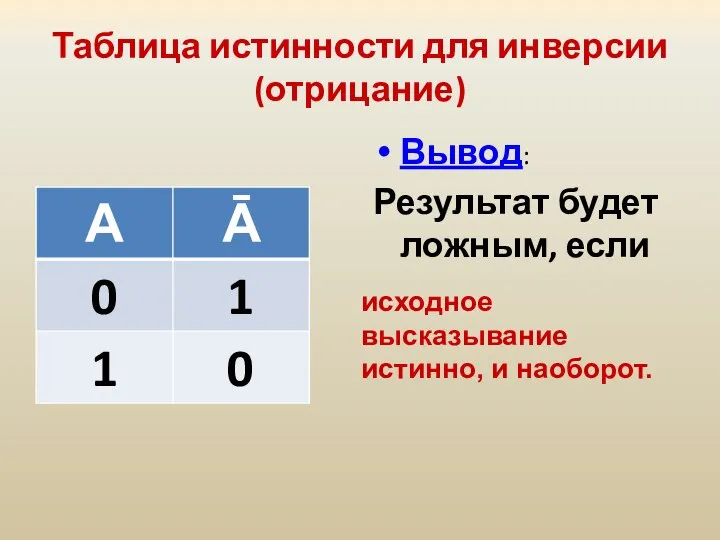
Таблица истинности для инверсии (отрицание)
Вывод:
Результат будет ложным, если
исходное высказывание истинно, и наоборот.

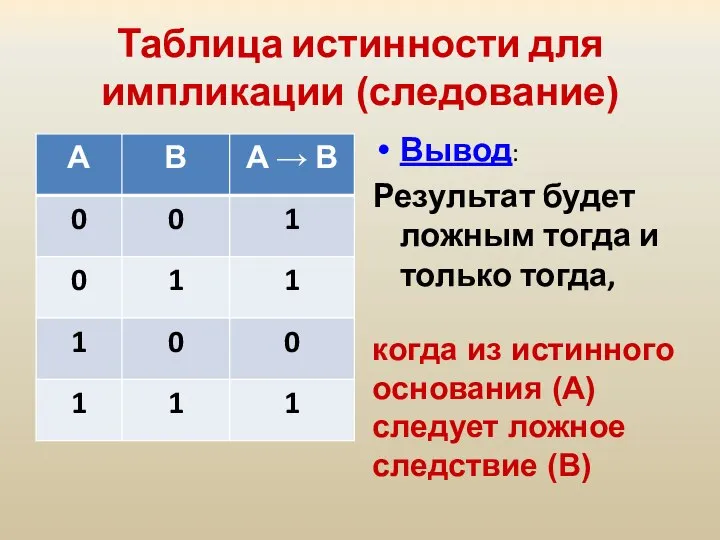
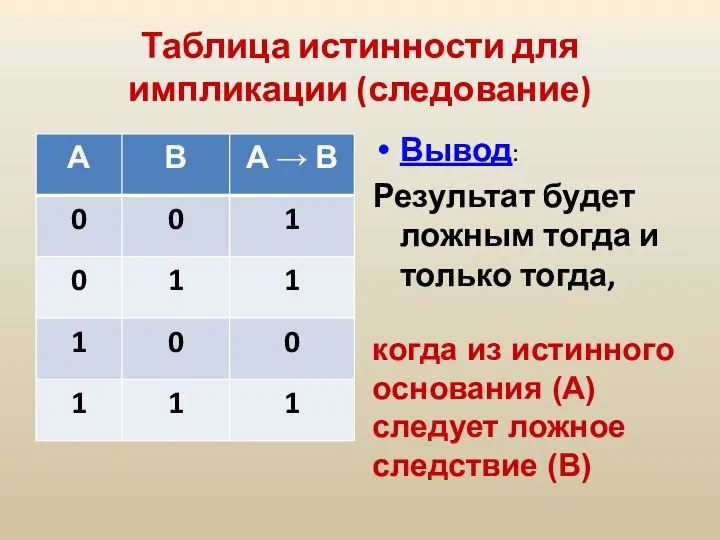
Таблица истинности для импликации (следование)
Вывод:
Результат будет ложным тогда и только тогда,
когда из истинного основания (А) следует ложное следствие (В)

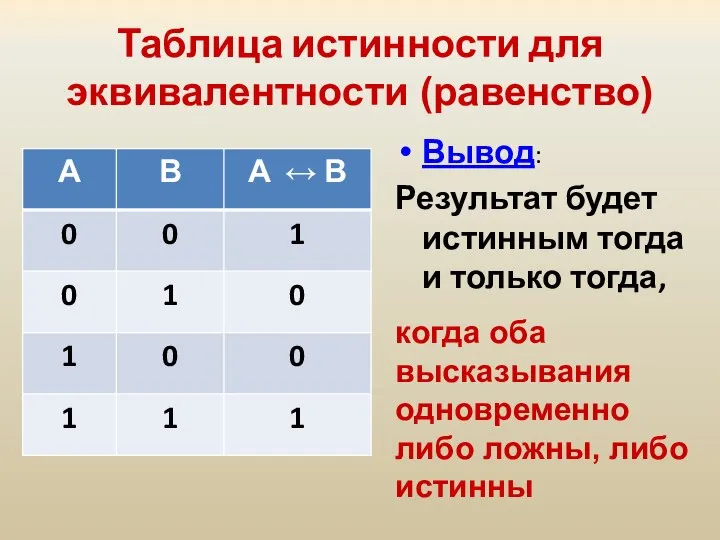
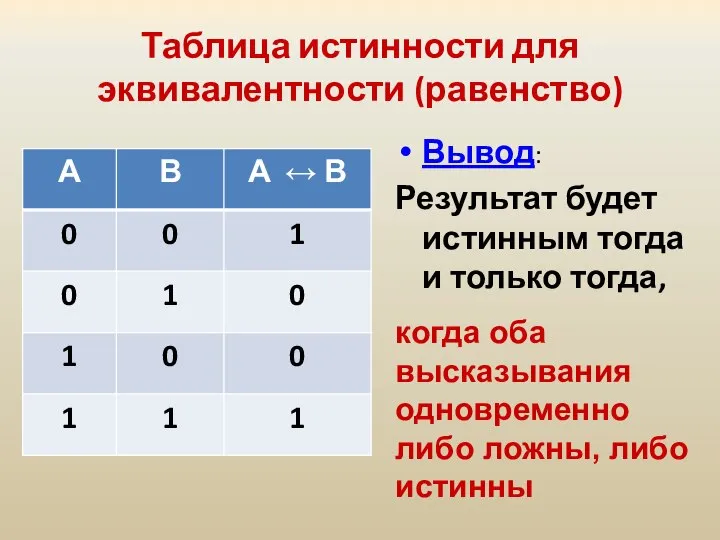
Таблица истинности для эквивалентности (равенство)
Вывод:
Результат будет истинным тогда и только тогда,
когда оба высказывания одновременно либо ложны, либо истинны

Если составное высказывание (логическую функцию) выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
истина ложь

Порядок выполнения логических операций:
Действия в скобках
Инверсия (отрицание ¬)
Конъюнкция (умножение И ∧)
Дизъюнкция (сложение ИЛИ ∨)
Импликация (следование →)
Эквивалентность (равенство ≡)

Повторяем

Таблица истинности для конъюнкции (умножение)
Вывод:
Результат будет истинным тогда и только тогда, когда
оба исходных высказывания истинны

Таблица истинности для дизъюнкции (сложение)
Вывод:
Результат будет ложным тогда и только тогда,
когда оба исходных высказывания ложны, и истинным
во всех остальных случаях

Таблица истинности для инверсии (отрицание)
Вывод:
Результат будет ложным, если
исходное высказывание истинно, и наоборот.

Таблица истинности для импликации (следование)
Вывод:
Результат будет ложным тогда и только тогда,
когда из истинного основания (А) следует ложное следствие (В)

Таблица истинности для эквивалентности (равенство)
Вывод:
Результат будет истинным тогда и только тогда,
когда оба высказывания одновременно либо ложны, либо истинны

Импликация (Следование)
когда из истины следует ложь
Вывод:
Результат будет ложным тогда и только тогда,
Пример

Число 376 четное и трехзначное
Зимой дети катаются на коньках и на лыжах
Новый год мы встретим на даче либо на Красной площади
Неверно, что Солнце движется вокруг Земли
Если 10 октября будет солнечным, то зима будет теплой
Земля имеет форму шара, который из космоса кажется голубым
На уроке математики старшекурсники отвечали на вопросы преподавателя, а также писали самостоятельную работу
Если вчера было воскресенье, то Дима вчера не был в институте и весь день гулял
Если сумма цифр натурального числа делиться на 3, то число делиться на 3
Число делится на 3 тогда и только тогда, когда сумма цифр числа делится на 3

Вопрос 1
1)Операция, соответствующая связке “ИЛИ” называется…………..
2)Обозначается……
3)Истинна тогда……

Вопрос 2
1)Операция, соответствующая союзу “И” называется…………..
2)Обозначается……
3)Истинна тогда……

Вопрос 3
1)Операция, соответствующая связкам “ЕСЛИ ..., ТО”, “ИЗ ... СЛЕДУЕТ”, “... ВЛЕЧЕТ ...”, называется…………..
2)Обозначается……
3)Ложь тогда……

Вопрос 4
1)Операция, соответствующая связкам “тогда и только тогда”, "необходимо и достаточно”, “... равносильно ...”, называется…………..
2)Обозначается……
3)Истинна тогда……

№6_1 Обозначьте простые высказывания логическими переменными А и В и запишите логическую операцию
Марина старше Светы. И Оля старше Светы

2. Половина класса изучает английский язык или немецкий
№6_2 Обозначьте простые высказывания логическими переменными А и В и запишите логическую операцию

№6_3 Обозначьте простые высказывания логическими переменными А и В и запишите логическую операцию
3. В кабинете есть учебники. В кабинете есть справочники.

№6_4 Обозначьте простые высказывания логическими переменными А и В и запишите логическую операцию
4. Слова в этом предложении начинаются на букву Ч. Слова в этом предложении начинаются на букву А.

№6_5 Обозначьте простые высказывания логическими переменными А и В и запишите логическую операцию
3. Часть туристов любит чай. Остальные туристы любят молоко

№6_6 Обозначьте простые высказывания логическими переменными А и В и запишите логическую операцию
3. Синий кубик меньше красного. Синий кубик меньше зеленого

№6_7 Обозначьте простые высказывания логическими переменными А и В и запишите логическую операцию
3. Х=3, Х>2

Построение таблиц истинности
Для решения логического выражения необходимо построить таблицу истинности. Это таблица, в которой по действиям показано, какие значения принимает логическое выражение при всех возможных наборах значений логических переменных.