10-14-Двоичное представление отрицательных чисел

Терминология
Разрядная сетка – количество разрядов в записи двоичного числа
Знаковый разряд – старший бит в записи двоичного числа
Информационные разряды – разряды в записи двоичного числа после знакового, т.е. с нулевого до знакового.
Переполнение разрядной сетки – получение числа, количество разрядов которого превышает разрядную сетку.

Терминология
Прямой код – обычный способ представления положительного двоичного числа.
Обратный (инверсный) код – способ записи двоичного числа, каждый разряд которого инвертирован из прямого кода.
Дополнительный код – способ записи отрицательного числа, получаемый из обратного кода увеличением его значения на единицу

Особенности двоичной арифметики
Все вычисления выполняются в рамках разрядной сетки, т.е. все числа «одинаково-разрядные».
Диапазон вычислений ограничен разрядной сеткой: для 8 разрядов диапазон чисел либо 0…255 (0…28-1) для натуральных чисел, либо -127…127 (-27-1…27-1) для целых
Каждое число записывается в двоичном коде без знака
Знак для целых чисел задается цифрой старшего разряда:
«0» для положительных, «1» для отрицательных;
Положительные числа принято представлять в прямом коде
Отрицательные числа представляются либо в дополнительном, либо в обратном коде.

Кодовое представление числа
Знак Информационные разряды
Разрядная сетка
Знак Информационные разряды
Пример представления положительного целого числа
Х= + 5

Кодовое представление числа
Знак Информационные разряды
Х= – 5
Разрядная сетка
Знак Информационные разряды
«Интуитивное» представление отрицательного целого числа
Х= + 5

Кодовое представление числа
Знак Информационные разряды
Х= – 5
Разрядная сетка
Знак Информационные разряды
«Интуитивное» представление отрицательного целого числа
НЕВЕРНОЕ
Х= + 5

Для чего нужны отрицательные числа?
Понятие «отрицательного» числа позволяет заменить понятие «разность» положительных чисел на «сумма» положительного и отрицательного числа, т.е. двух целых чисел.
Это позволит компьютеру освоить только одну «программу» - суммирование чисел вместо двух: суммирование и разность

Как компьютер определяет,
как закодировано число?
Однобайтовое двоичное число может быть задано как в прямом, так и в дополнительном или обратном коде.
Способ представления двоичного числа определяется из блока описания переменных программы (и никак иначе).
Например,
Var a: byte; {a – целое положительное число 0…255 }
Var x: short; {x – целое число со знаком -127…+127 }

Обратный код
Применяется для преобразования операции вычитания в операцию сложения.
Совпадает с прямым кодом для положительных чисел.
Представляет собой инверсию прямого кода записи двоичного отрицательного числа.
Практически не используется в настоящее время

Обратный код
Порядок получения обратного кода отрицательного числа:
Записать двоичное представление модуля отрицательного числа
Дописать незначащие «нули» слева от информационных до заполнения разрядной сетки
Заменить во всех разрядах 0 ? 1; 1 ? 0
Пример:
х10=-5 =>|х2| = 1012 =>
|х2| = 000001012 =>
x2 = 111110102

Обратный код
Недостаток: существуют два «нуля»:
положительный (0000 0000) и
отрицательный (1111 1111), что усложняет техническую реализацию вычислительного процесса суммирования чисел
Разряд, «выпадающий» из разрядной сетки при суммировании, добавляется в младший разряд результата
Чтобы получить прямой код модуля отрицательного числа, нужно инвертировать все его разряды

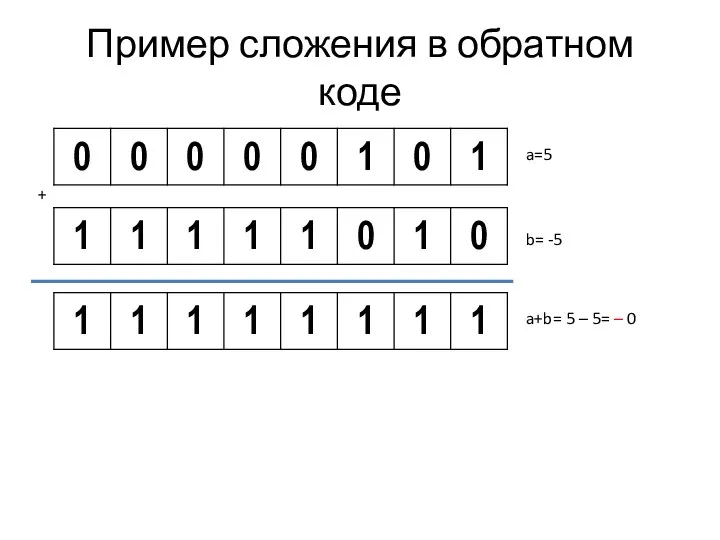
Пример сложения в обратном коде
a=5
b= -5
+
a+b= 5 – 5= – 0

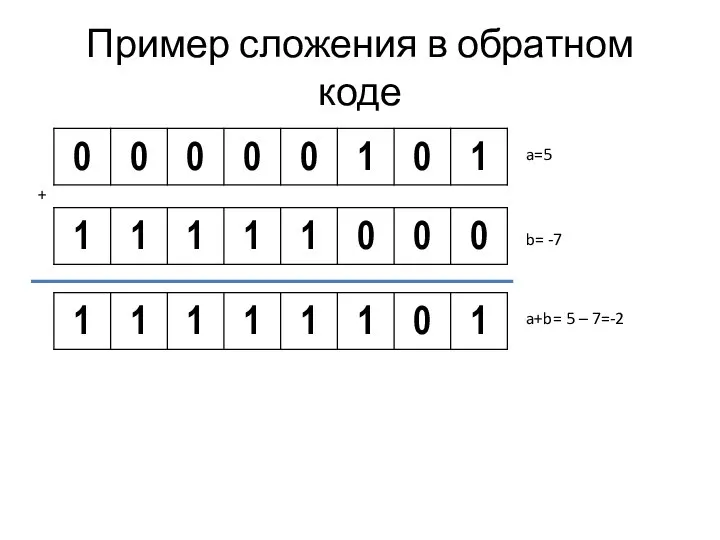
Пример сложения в обратном коде
a=5
b= -7
+
a+b= 5 – 7=-2

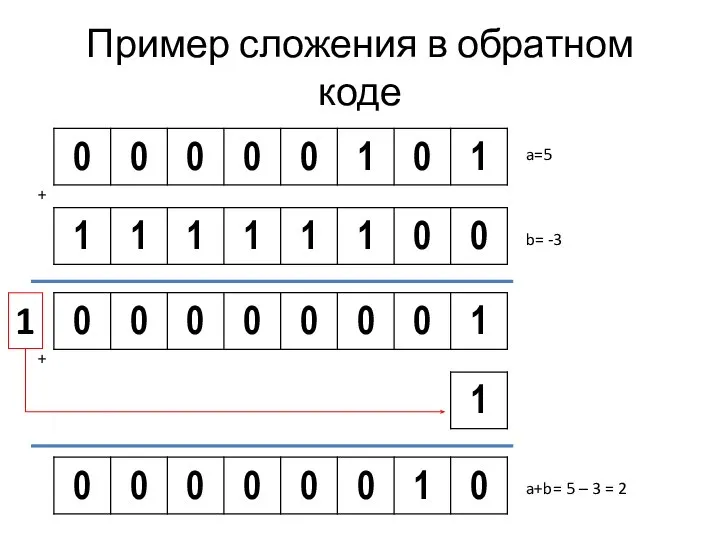
Пример сложения в обратном коде
a=5
b= -3
+
a+b= 5 – 3 = 2
+
1

Дополнительный код
Применяется для преобразования операции вычитания в операцию сложения.
Совпадает с прямым кодом для положительных чисел.
Представляет собой инверсию прямого кода записи двоичного отрицательного числа, дополненную единицей. Такой алгоритм позволяет исключить «двойной ноль»
Применяется в настоящее время

Дополнительный код
Порядок получения дополнительного кода отрицательного числа:
Записать двоичное представление модуля отрицательного числа
Дописать незначащие «нули» слева от информационных до заполнения разрядной сетки
Заменить во всех разрядах 0 ? 1; 1 ? 0
Прибавить единицу
Пример:
х10=-5 => |х2| = 1012 =>
|х2| = 000001012 =>
х2 = 111110102 +1 = 111110112

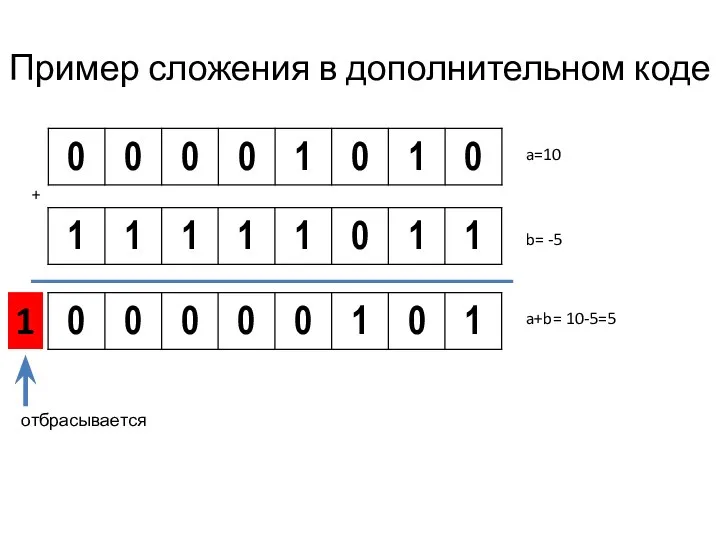
Пример сложения в дополнительном коде
a=10
b= -5
+
a+b= 10-5=5
1
отбрасывается

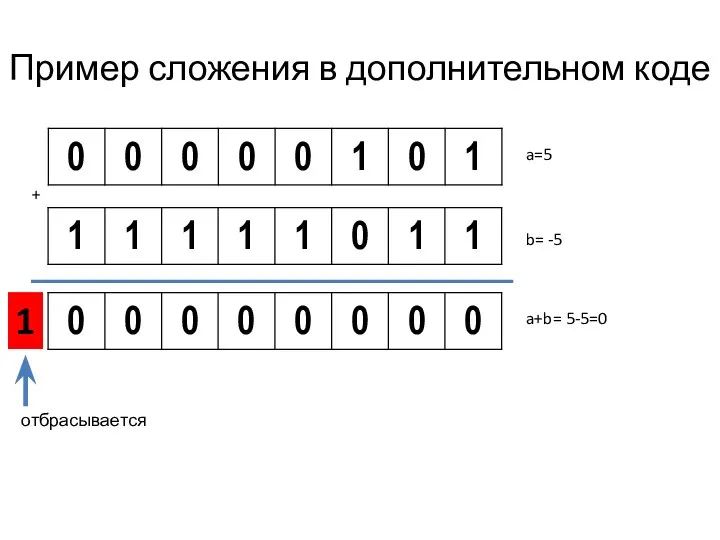
Пример сложения в дополнительном коде
a=5
b= -5
+
a+b= 5-5=0
1
отбрасывается

Дополнительный код
Вычитание заменяется сложением чисел в дополнительном коде
Чтобы получить прямой код модуля отрицательного числа, нужно определить его дополнительный код
Пример:
х10=-5=> х2 = 11110112 =>
|х2|= 00001002+1 =>
|х2|= 00001012

Примеры заданий
Используя восьмибитное представление чисел:
вычислить значение, заменяя вычитание «сложением» чисел в обратном коде:
12-12, 17-12, 13-19
вычислить значение, заменяя «вычитание» «сложением» чисел в дополнительном коде:
12-12, 17-12, 13-19